基于集合经验模态分解和随机森林的短时交通流预测

田佳, 王德勇, 师文喜

(1.新疆大学信息科学与工程学院, 乌鲁木齐 830017; 2.新疆联海创智信息科技有限公司, 乌鲁木齐 830011;3.中国电子科学研究院, 北京 100041)

近年来,随着经济的快速发展和人们生活水平的提高,机动车保有量与日俱增,随之而来的交通拥堵和能源浪费等问题也日趋严重。在这一背景下,智能交通系统的应用越来越受到交通管理部门的关注[1]。短时交通流研究作为智能交通系统的重要组成部分,可以为交通引导和道路管理提供便利,是交通领域研究的重要内容[2]。短时交通流预测是指利用历史交通流数据,实时预测未来较短时间内的交通流[3];通常基于交通流的三大参数,即平均车流量、平均车速、平均占有率等进行相关研究[3]。

短时交通流预测方法可以分为统计分析、非线性理论、仿真预测、智能预测和组合预测五大类[3-4]。但面对复杂且不确定的交通数据,并不存在一种算法可以在任何条件下都能具备良好的性能,因此,研究人员就提高模型预测精度和扩大其适用范围展开了大量的研究。Yu等[5]提出了一种基于长短时记忆神经网络(long short-term memory,LSTM)的短时交通流预测模型,并在高速公路数据集上验证了该模型的泛化能力。但是LSTM存在参数选择困难、易陷入局部最优解及收敛速度慢等问题。鉴于以上问题,Liu[6]为提高模型预测精度,提出了一种基于支持向量回归(support vector regression,SVR)的交通流预测模型,并通过实验证明,相比LSTM模型,该模型具有更好的预测效果。但是SVR对于复杂的预测样本难以选取合适的核函数,从而对实际具有干扰的短时交通流时间序列预测性能有所欠缺。基于此,邹宗民等[7]利用粒子群优化算法对SVR的参数进行寻优,实验证明,该方法可进一步提升SVR的预测精度。冒云香等[8]结合随机森林训练速度快、参数简单、预测精度高及对输入数据不敏感等优点,构建了一种基于随机森林的短时交通流预测模型,并通过实验验证了该模型的可行性和有效性。因此,在前人的研究基础上,现选用随机森林进行下一步研究。同时,随着对短时交通流研究的不断深入,发现许多文献都将注意力集中在提高模型的预测性能上,忽略了交通流数据本身存在的可预测性[9-10]。于是,方方等[3]将小波分析与集成学习算法进行组合,对短时交通流进行预测,实验结果表明,相比单一的预测模型,组合模型能进一步提升模型预测效果。但是小波分析中的小波基函数和分解层数都存在较大的人为选择性,容易产生虚假分量。而集合经验模态分解(ensemble empirical mode decomposition,EEMD)是根据数据本身的时频尺度特征,将原始数据分解为若干个本征模函数(intrinsic mode function,IMF)和一个残差分量(residual,RES);然后根据各个分量的特点构建模型并进行整合,从而有效提高模型预测精度。殷礼胜等[11]提出了一种基于EEMD与最小二乘支持向量机(least squares support vector machine,LSSVM)相结合的组合模型,结果表明相比LSSVM模型,组合模型具有更高的预测性能。Tang等[9]提出了一种基于EEMD与模糊C均值神经网络(fuzzyC-means neural network,FCMNN)相结合的交通流组合预测模型,实验结果表明相比FCMNN模型,引入EEMD的FCMNN组合模型预测精度得到显著提升。由此可见,将EEMD与其他智能算法结合起来对短时交通流进行预测,可有效提高模型的预测精度。

基于上述研究,现提出一种基于EEMD和随机森林(random forest,RF)[12]的短时交通流预测模型。EEMD可将复杂的、非线性的短时交通流数据分解为若干个不同时间尺度下相对平稳的序列,细化交通流数据的信息;同时,RF不仅克服了LSTM训练速度慢、易陷入局部最优解等问题,还解决了SVR参数选择困难的困境,从而使用EEMD与RF相结合的方法对于短时交通流预测能够达到较好的预测效果。首先,利用EEMD将原始短时交通流数据分解为若干个子序列;接着,对IMF1进行EEMD分解;随后将各个子序列分别使用RF进行预测,同时通过学习曲线和交叉验证的方法选取模型最优参数组合;最后将各子模型的预测结果线性求和,得到模型最终的预测结果,并在阿拉尔市内路段的真实数据集上进行验证实验。

1 关键技术与算法

1.1 集合经验模态分解

为解决经验模态分解(empirical mode decomposition,EMD)过程中出现的模态混叠现象,EEMD向原始数据中加入白噪声进行扰动,并通过足够的实验次数将添加的白噪声平均化而使最终得到的分量保持物理上的唯一性[11,13-14]。EEMD的具体步骤如下。

步骤1向原始数据X(t)中加入白噪声ω(t),得到新的序列X′(t)。

X′(t)=X(t)+ω(t)

(1)

步骤2计算出X′(t)的所有上、下极值点,并画出上、下包络线U(t)和L(t),再求上、下包络线的均值,得到均值包络线G(t)。

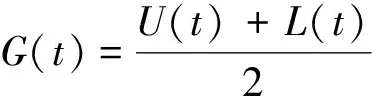
(2)

步骤3使用X′(t)减去G(t),得到中间序列H(t)。

H(t)=X′(t)-G(t)

(3)

步骤4判断中间序列H(t)是否满足IMF的两个条件,若满足,则该序列就是一个IMF分量;反之,以该序列为基础,重新做步骤2～步骤4的分析,直到满足条件为止。IMF的两个具体条件为:在整个数据段内,极值点的数量必须和过零点的数量相等或相差不超过一个;在任意时段,上包络线和下包络线均值都为零,即上、下包络线相对于时间轴对称。

步骤5经过以上步骤得到第一个IMF后,用X′(t)减去该IMF分量,并将其作为新的序列,重复步骤2～步骤4,得到m个IMF和1个RES。

(4)

步骤6重复加入噪声M次进行分解,即重复M次步骤1～步骤5操作。

步骤7将上述每次分解得到的相同序号的IMF分量求平均值得到最终的IMF分量Ij(t)。

(5)

式(5)中:Ii,j(t)为第i次加入噪声分解得到的第j个IMF分量;Ij(t)为最终的第j个IMF分量。

1.2 随机森林算法

RF是一种集成学习算法,它由两个部分组成:决策树和Bagging算法[12]。决策树是一种基于树结构进行判断决策的有监督模型,它由根节点、中间节点和叶节点构成。Bagging算法的主要思想是:通过有放回抽样的方式从训练集中抽取多个样本,再对每轮获取的子训练集,分别训练各自的模型。RF是由许多决策树构成的,其中不同决策树之间没有关联。RF回归算法的构造步骤如下。

步骤1从原始训练集中有放回的抽取n次,一次抽取一个样本,最终得到由这n个样本组成的子训练集X′。

X′={(x1,y1),(x2,y2),…,(xn,yn)}

(6)

式(6)中:xi∈Rn为输入值;yi∈R为输出值。

步骤2从样本的h个属性中随机选取m个属性构成特征子集T′。

T′={t1,t2,…,tm},m≪h

(7)

步骤3基于X′和T′,构建CART回归树,即通过求解式(8),选择最优切分变量t∈T′与它的取值s,得到最优的(t,s)组合。

(8)

式(8)中:Ri为第i个子区域;ci为第i个子区域的输出值。

步骤4对选定的(t,s)划分区域并计算相应的输出值。

R1(t,s)={x|xt≤s},R2(t,s)={x|xt>s}

(9)

(10)

步骤5继续对两个子区域调用步骤3、步骤4,直至满足停止条件。

步骤6随后输入空间被划分为M个区域R1,R2,…,RM,构成决策树,其输出值计算公式为

(11)

步骤7按照步骤1～步骤6建立K棵决策树,这样就构成了RF。

步骤8对每棵决策树的输出值求取简单平均值或者加权平均值,可得到RF的最终值,分别如式(12)和式(13)所示。

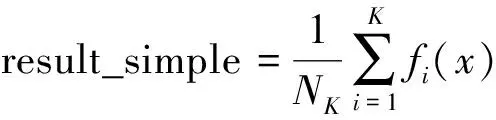
(12)

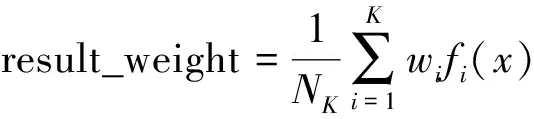
(13)

1.3 EEMD-RF组合模型

由于短时交通流的非线性、不确定性等特性,单一的预测模型很难取得较好的预测结果[3,11]。故将EEMD对非线性数据分解的优势与非线性模型RF结合起来进行预测。然而,对短时交通流进行一次EEMD分解后,低频的序列可以较好地拟合,高频的序列拟合误差较大,为缓解这一现象,将一次分解后拟合效果最差的高频IMF1分量进行EEMD二次分解。EEMD-RF预测模型框架如图1所示,其具体操作步骤如下。

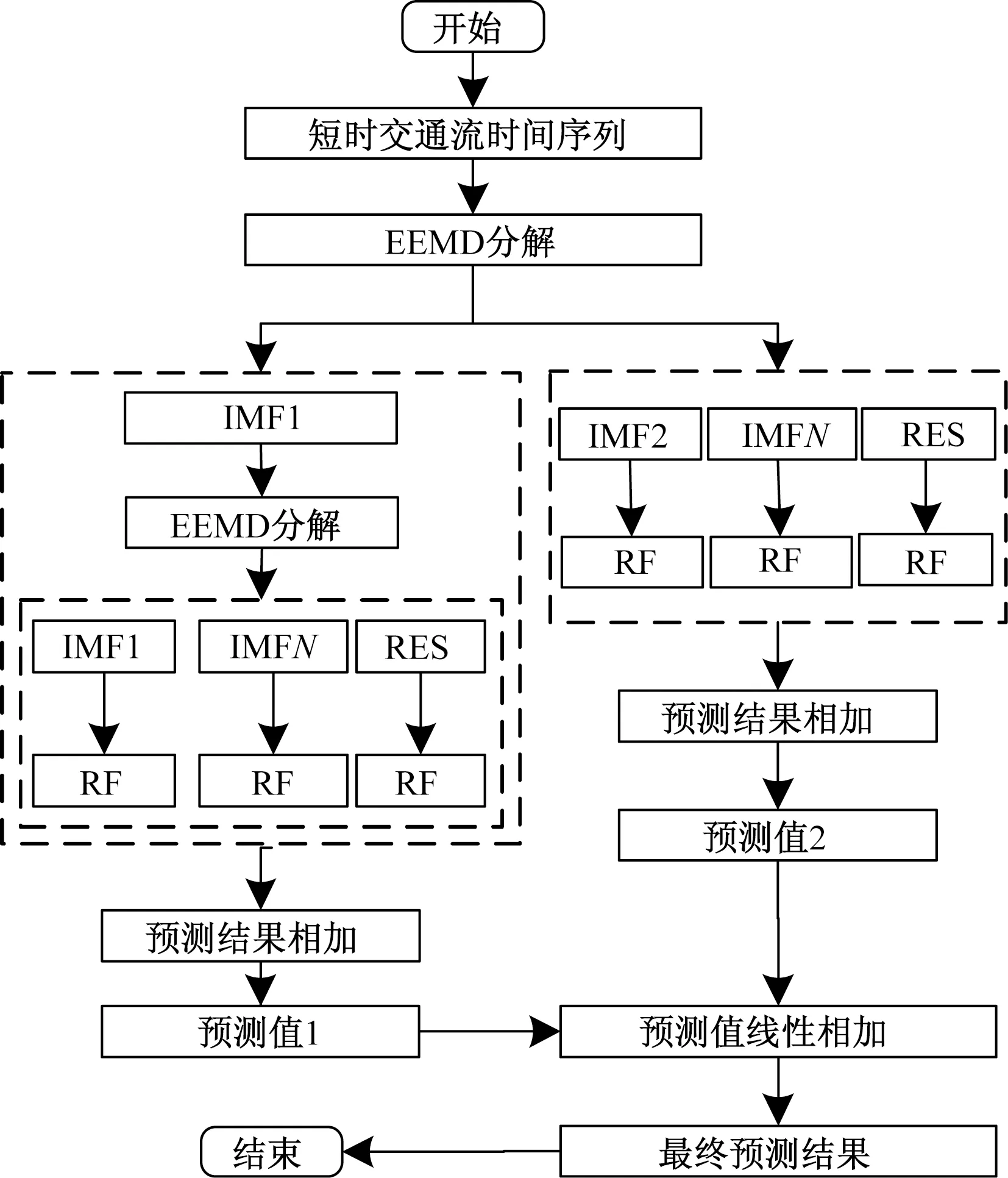
图1 EEMD-RF模型框架Fig.1 EEMD-RF model framework

步骤1利用EEMD对原始时间序列数据进行分解,得到若干个IMF分量和1个RES分量。

步骤2将步骤1的各个分量划分为训练集、验证集及测试集。

步骤3在训练集上对每个分量构建RF模型,并在验证集上使用交叉验证的方法验证模型的泛化能力,最后利用泛化能力最强的RF模型参数组合来训练RF模型,并对测试集进行预测。交叉验证结果和样本预测值计算分别如下。

(14)

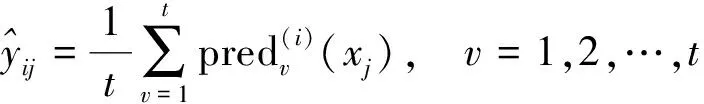
(15)

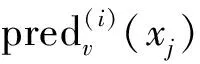
步骤4利用模型评估指标分析各个RF模型的预测性能,并将最高频IMF1分量进行二次EEMD分解,即重复步骤2、步骤3,随后将二次分解各分量预测值线性相加,得到IMF1二次分解预测值。

步骤5将所有RF模型的预测值线性相加,得到最终预测结果。

2 案例分析

2.1 数据预处理

选取阿拉尔市一段道路高清卡口系统采集的过车数据进行实验,采集时间为2019年10月26日—11月29日,共35 d,该实验设定时间间隔为10 min。在进行实验之前,需要对卡口数据进行预处理,处理框架如图2所示,其步骤描述如下。

图2 数据预处理框架Fig.2 Data preprocessing framework

步骤1去除原始数据中的重复数据和缺失数据。

步骤2使用SQL语句,筛选出经过研究路段的车辆,并统计车辆的行驶时间。

步骤3去除步骤2中由于中途停车和超速行驶导致的异常数据。

步骤4以10 min为统计时窗,当统计时窗内的样本数量小于3条时,则认为该统计时窗内缺失数据,选用合适的缺失值填补策略进行处理,其中,当数据为单个缺失时,采用时间序列填补策略进行填补,即使用前3个统计时窗的平均值进行填补,但当数据为连续缺失时,采用历史数据填补策略进行填补,即使用历史相同统计时窗的数据进行填补;反之,则认为存在异常值,使用箱型图法去除异常值[15,17]。

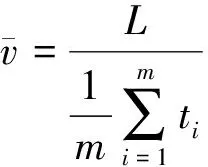
(16)

式(16)中:L为路段长度;m为统计时窗内车辆数量;ti为第i辆车的行驶时间。

2.2 特征提取

交通流数据是典型的时间序列数据,因此可以从该序列中提取出具有时间特性的元素[16]。

(1)工作日与非工作日特性。交通流数据在工作日会出现明显的上下班高峰,相较于非工作日,规律性更强。由此,提取DayOfWeek这一特性,例如周一则将DayOfWeek标记成1;再提取IsWeekend这个特性,例如周末就将IsWeekend标记成1,否则标记成0。

(2)日期特征。为细化交通流数据的时间特性,可以提取出其日期特征,即提取每条记录统计时段的年、月、日、时、分,例如统计时窗的起始时间为“2019-10-26 09:10:00”,可以提取出来的时间特征为“2019”“10”“26”“09”“10”。因实验数据的年和月两个时间尺度对实验结果基本无影响,故只提取日、时与分3个特征。

(3)周期特征。周期特征分两类进行考虑,一类是当前时间段的前若干个连续时间段的交通流会对当前的交通流产生影响。例如第i天的[10:00,10:10]的交通流受第i天的[09:50,10:00]、[09:40,09:50]、[09:30,09:40]等n个时间段的影响。另一类是同一段路每天相同时间段的交通流变化具有相似,因此,预测第k日的[10:00,10:10]的交通流,可以将第k-1,k-2,…,k-m日[10:00,10:10]的交通流作为特征值。其中,n和m的最佳值通过后续实验进行选取。

2.3 超参数优化及评估指标

评估模型前,首先确定需要优化的超参数,包括决策树的数量ntrees、决策树最大层数md、划分节点的最少样本数mss和叶子节点最少样本数msl。初始化超参数的搜索空间,ntrees为[2,300],md为[2,51],mss为[2,30],msl为[1,30]。同时,通过绘制学习曲线和交叉验证的方式对超参数依次调优,并根据评估指标对其预测效果进行判断,从而确定最优的参数组合。选择4个模型指标对模型的预测性能进行评估,分别为均方根误差(root mean squared error,RMSE)、平均绝对误差(mean absolute error,MAE)、均方误差(mean square error,MSE)、平均绝对百分比误差(mean average precision,MAPE)。计算公式分别如式(17)～式(20)所示。

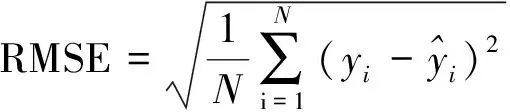
(17)

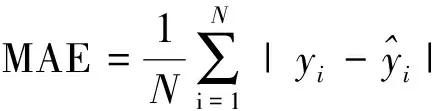
(18)

(19)

(20)

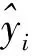
2.4 模型训练与预测

考虑到在午夜和凌晨这两个时间段车流量较少,进行交通流预测的现实意义不大[16],故根据地域作息时间,从经过上述预处理的5 040条数据中选取每天10:00—22:00的时间段进行实验。最后,用于实验的数据共2016条结果如图3所示。

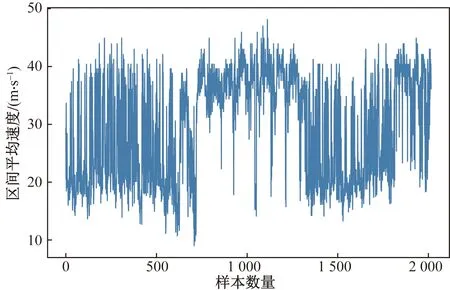
图3 交通流波动图Fig.3 Traffic flow fluctuation chart

为确定n和m的值,选取n的值为2～12,即预测时间段的前20 min～2 h;m的值为1～7,即预测时间段前1 d～1周,进行实验,故用于EEMD分解的数据共2 940条,其分解结果如图4所示。

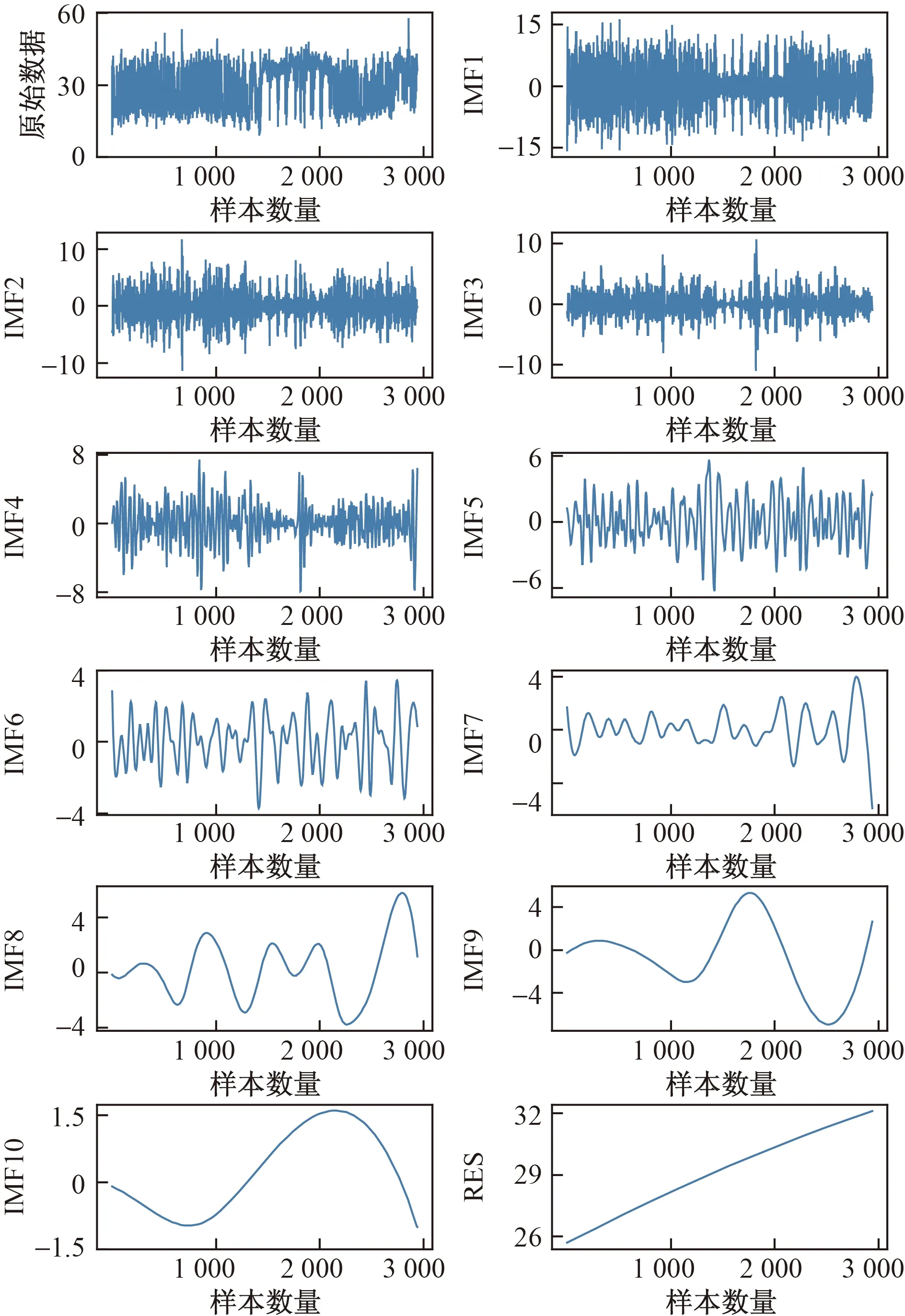
图4 经EEMD分解后的交通流序列Fig.4 Traffic flow sequence decomposed by EEMD

随后,将分解得到的IMF1～RES处理成式(21)的形式,如图5所示。

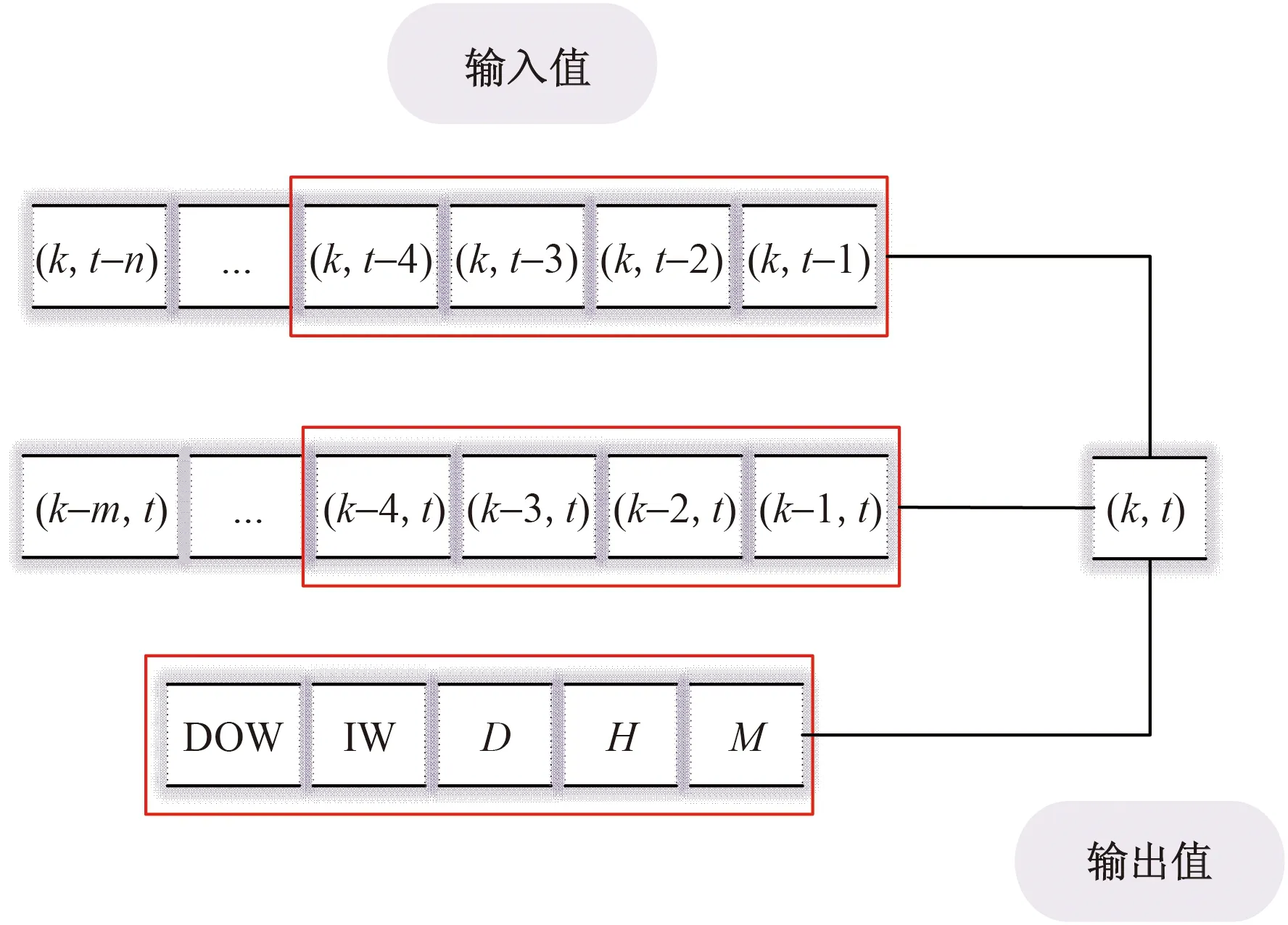
图5 样本数据结构图Fig.5 The structure diagram of sample data

x(k,t)={x(k,t-1),x(k,t-2),…,x(k,

t-n),DOW,IW,D,H,M,x(k-1,t),

x(k-2,t),…,x(k-m,t)}

(21)

式(21)中:x(k,t)为第k天第t时段的交通流;x(k,t-n)为当前时段前n个时间段的交通流;DOW为DayOfWeek的值;IW为IsWeekend的值;D代表天,H代表时,M代表分,x(k-m,t)代表当前时段前m天同时段的交通流数据。并将处理后的数据划分为训练集、验证集和测试集,划分比例分别为75%、15%和10%。

其中,模型预测效果随m和n取值变化的曲线图分别如图6和图7所示。

图6 参数n的变化图Fig.6 Curve graph of n

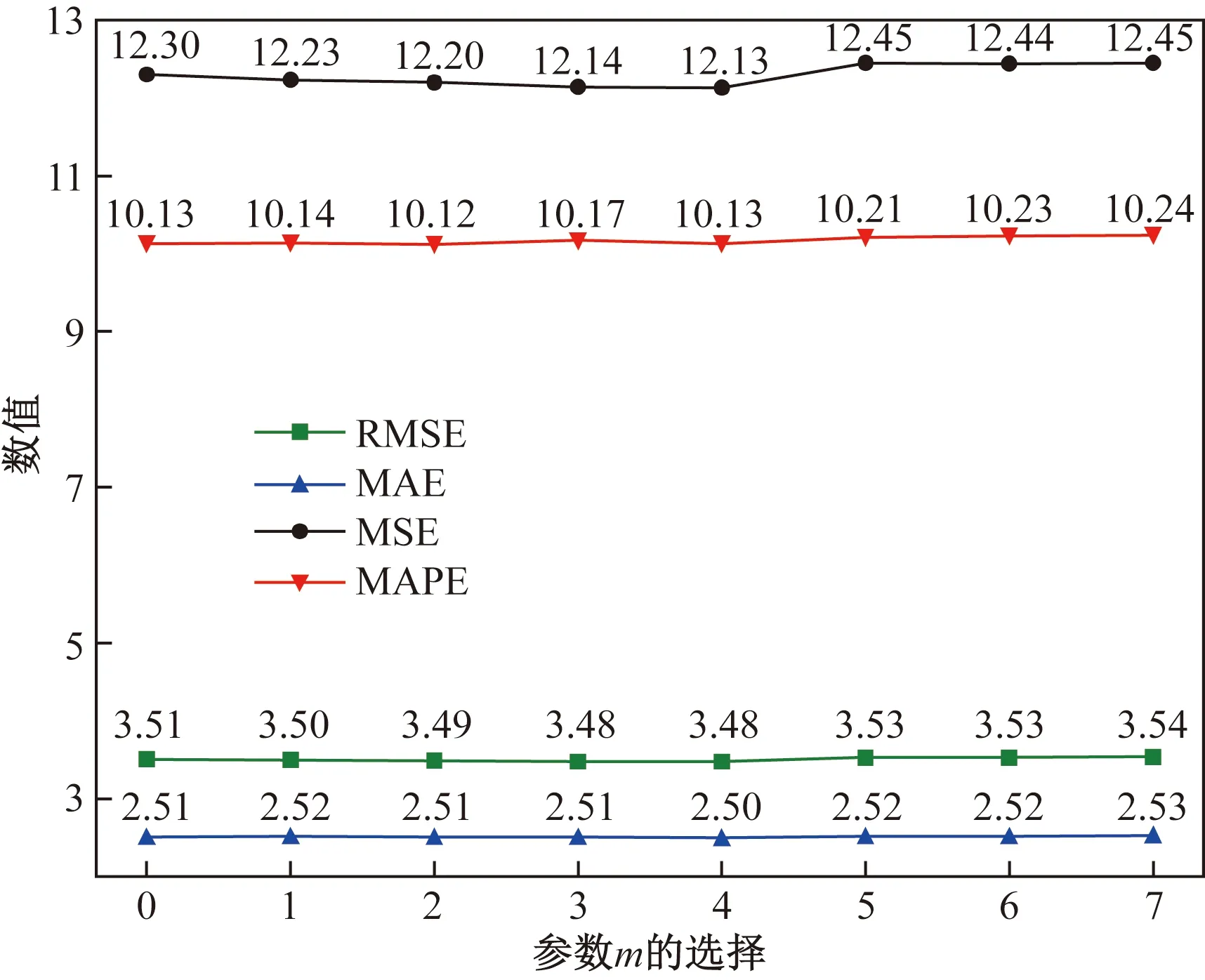
图7 参数m的变化图Fig.7 Curve graph of m

从图6可以看出,随着参数n的变化,RMSE在3～4波动,MAE在2～3波动,MAPE在10～11波动,并且这3个模型评估指标的整体波动幅度都不大,换言之,参数n的变化对模型的RMSE、MAE、MAPE值影响较小,而MSE在12～14波动,其波动幅度较大,具体表现为,在2～10呈现缓慢下降的趋势,在10～12呈现缓慢上升的趋势,且在取值为10时达到最小值。因此,综合考虑RMSE、MAE、MSE和MAPE这4个模型评估指标的效果,认为前10个时间间隔的交通流数据对该时段产生的影响最大。因此,最终选择n=10进行后续的实验。

从图7可以看出,随着参数m的变化,RMSE、MAE、MAPE和MSE的整体波动幅度不大,RMSE和MSE在0～4呈现缓慢下降的趋势,在4～7呈现缓慢上升的趋势。因此,综合RMSE、MAE、MSE和MAPE 这4个指标的结果,可以看出预测结果相差较小,前几天同一时段的交通流变化对预测结果影响不大,即历史前几天同时段的交通流对最后的预测精度影响较小。最后综合考虑,最终选择预测效果最好的m=4进行后续的实验。原始数据经过EEMD一次分解后,各个分量的模型参数和模型评估结果分别如表1和表2所示。

表1 11个子模型预测性能评估结果

表2 11个子模型预测性能评估结果

同时,为进一步提高模型效果,将IMF1分量进行EEMD分解,如图8所示,随后,使用RF对每个分量进行预测,IMF1分解前后的模型预测结果对比如表3所示。

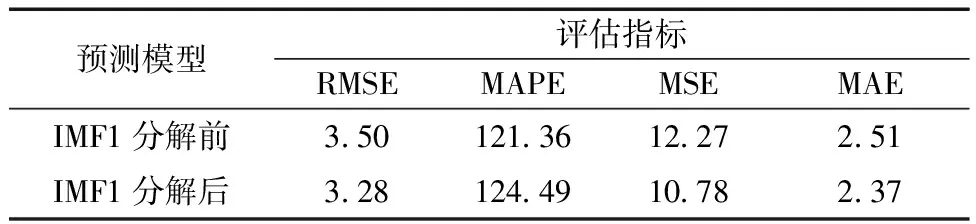
表3 IMF1模型预测性能结果

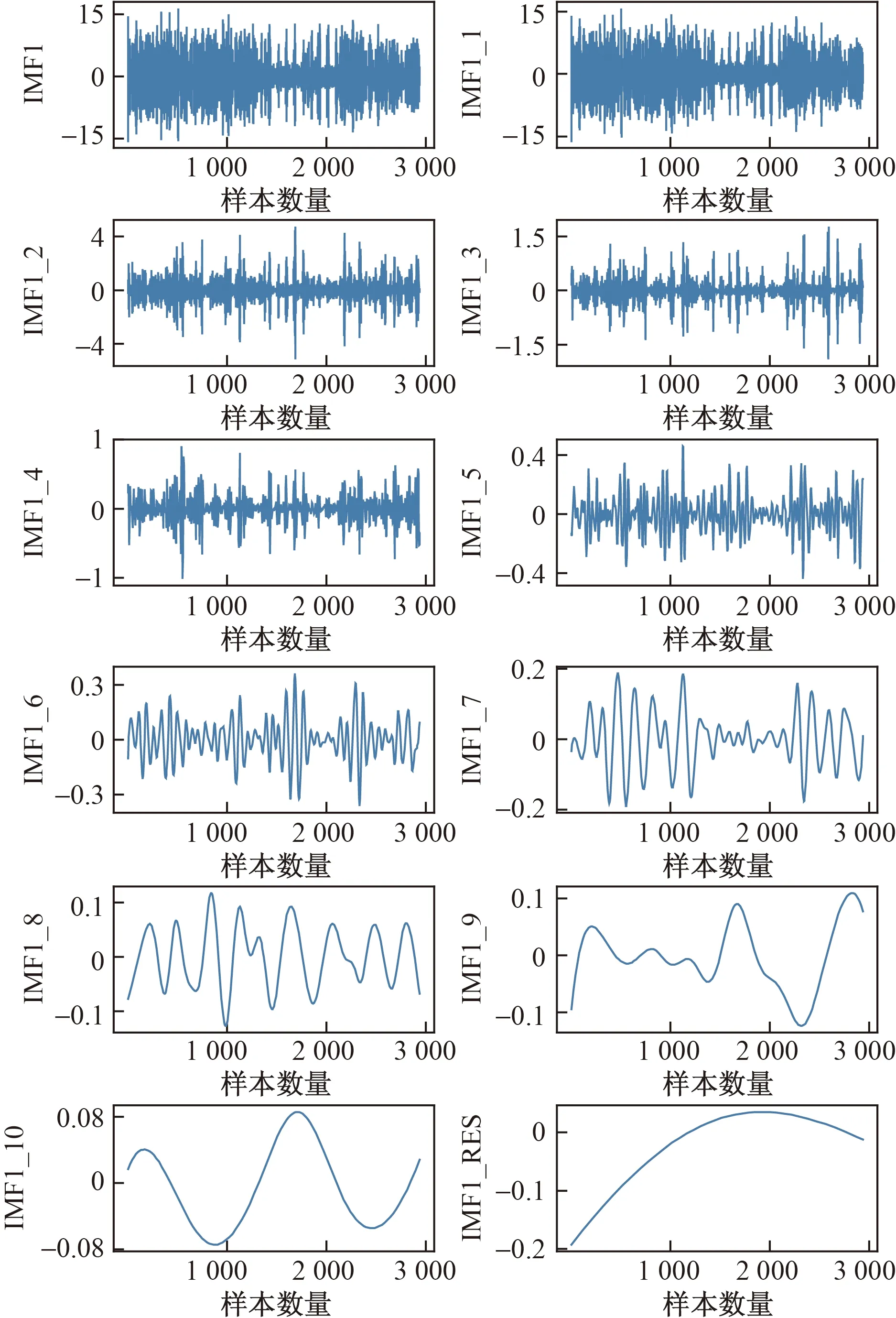
图8 IMF1经EEMD分解后序列Fig.8 IMF1 sequence decomposed by EEMD

由表3可见,IMF1进行EEMD分解后,在RMSE、MSE和MAE这3个评估指标中,相比未分解时的评估结果分别减少了6.29%、12.14%、5.58%。可见将高频IMF1分量进一步分解,可有效提高模型的预测性能。

2.5 实验结果分析

为了验证本文模型的有效性,分别对原有的交通流数据建立RF模型、一次EEMD-RF模型及本文EEMD-RF模型,进行对比实验,3种模型的对比预测效果和模型评估结果分别如图9和表4所示。

表4 模型预测性能评估结果

图9 各模型预测结果对比图Fig.9 Comparison of prediction results of different models

由表4可见,一次EEMD-RF模型的RMSE、MAE、MSE和MAPE均远高于RF模型,说明对数据进行EEMD分解可有效提升模型的预测性能,归根结底是EEMD能捕捉到交通流数据本身在不同时频的信息及其总体趋势,保证RF模型在了解交通流数据的总体趋势的同时能学习到数据内部的细节信息。同时,相较于一次EEMD分解与RF的组合模型,所提出的对高频分量IMF1进行二次EEMD分解,可在一定程度上进一步提升模型的预测性能,其原因是经过二次EEMD分解能更进一步细化高频分量IMF1中所包含的随机信息,提高模型精度。

3 总结

从提高交通流预测精度的角度出发,提出了一种基于EEMD和RF的交通流组合预测模型。通过实验结果可知,一次EEMD-RF模型预测效果明显优于单一的RF模型,并且本文提出的对高频分量IMF1进行二次分解的EEMD-RF模型可在一定程度上进一步提升模型的预测性能。但是,实际的交通流预测,还会受到许多其他因素的影响,比如上下游路段的时空相关性、天气、交通事故等,本文模型尚未将以上的因素考虑进来;同时,EEMD分解会增加模型的预测时间,因此在实时性要求较高的场景下,还需进一步研究分析。