基于车桥耦合分析的轨道交通系杆拱桥吊杆损伤识别研究

沈哲亮

（1.中铁第四勘察设计院集团有限公司,湖北 武汉 430063; 2.中国铁建股份有限公司桥梁工程实验室,湖北 武汉 430063）

0 引言

我国自20 世纪60 年代开始城市轨道交通桥梁建设，至今已有60 余年的历史，尤其是近年来，我国各大城市的轨道交通发展迅速，由于线路布置的需要，桥梁在线路中的占比越来越大。然而，钢管混凝土系杆拱桥也是近年来事故频出的桥型之一，事故隐患往往存在于吊杆，特别是短吊杆上。及时地对系杆拱桥的吊杆损伤进行检测和修复，对于保障桥梁结构的安全服役具有重要意义。

吊杆是系杆拱桥的主要承重构件之一，其受力状态是衡量系杆拱桥是否处于安全状态的重要参量。吊杆结构发生缺陷或损伤会引起索力变化及主梁内力重分布，因此可以利用吊杆的索力变化或主梁结构动力特性改变来识别吊杆的损伤。Shimada 等人通过实验的方法研究弯曲刚度对拉索张力识别的影响，提出在短索索力计算中，需要考虑弯曲刚度的影响。刘文峰[1]等针对索力测试问题，研究了边界条件在不同假设条件下的理论公式，表明弯曲刚度和边界条件对于短吊杆的索力测试是不可忽略的因素。盛宏玉、王国红[2]对现有的一些索力测试公式进行了误差分析，并对各索力测试公式根据索的长短给出了相对的应用范围。但是长短索的分界不仅与索的长度直接有关，还与吊杆的长细比、边界条件等其他因素有关，因此也有待进一步研究。

该文拟以系杆拱桥的结构动力特性为出发点，基于车桥耦合振动分析手段，分析列车过桥时，相应桥面位置的动位移、动应力、加速度及加速度变化率等动力响应指标的变化规律，探索吊杆结构损伤识别的新思路和方法。

1 频率法测索力及其局限性

频率法[3]由于其原理简单、操作方便、适用于施工阶段及成桥后等诸多优点而被广泛用于测试拉索索力。频率法测索力的基本流程见图1。

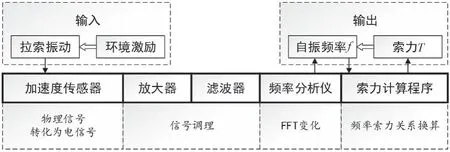
图1 频率法测索力基本流程

频率法的基本原理是张紧弦理论[4]，考虑抗弯刚度和边界条件影响，根据力学理论可以推导出自振频率与索力关系：

式中，fn——索的第n阶自振频率；l——索的计算长度；EI——索的抗弯刚度；k——边界条件影响系数，两端铰接时，k=4；两端固结时，k=1.814；一端固结一端铰接时，k=2.907。

从式（1）可以看出，抗弯刚度、计算长度和边界条件是影响频率索力关系的主要因素。对于长吊杆和柔性索来讲，抗弯刚度可以忽略不计，计算长度等于索的自由长度，边界条件可以看成两端铰接，因此以上参数可以比较准确地确定，频率索力关系明确。但是，对于短吊杆来说，不仅上述参数难以确定，还受其他外界因素影响。表1列出了频率法在短吊杆索力测试中的影响因素。

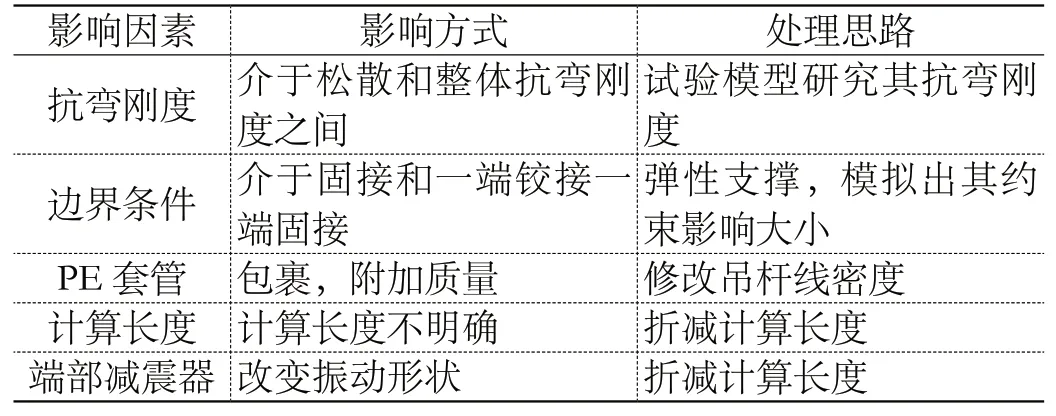
表1 频率法在短吊杆索力测试中的影响因素

从表1 可以看出，用频率法对短吊杆测试时，诸多参数难以确定，索力测试精度难以保证要求。尽管表1中提出了一些处理思路，但是针对性很强，不具有普遍性，因此频率法测试短吊杆索力具有很大的局限性。

2 基于车桥耦合分析的短吊杆损伤识别探索

2.1 车桥耦合模型

利用车桥耦合系统进行有限元分析，采用的计算原理是运用有限元方法分别建立桥梁模型和车辆模型[5]，基于模态叠加法分别形成桥梁子系统与车辆子系统的运动微分方程，通过拟力法将非线性阻尼力和非线性内力处理为虚拟力，以实现两个子系统内部的模态解耦，然后通过假定的轮轨之间的接触关系，使用迭代计算实现轮对与轨道之间的相互作用力和位移相协调。该文由于不考虑横向效应，因此轮轨关系假定为竖向始终密贴接触[6]。

2.1.1 车辆模型

该文以定员载重情况下的地铁A 型车作为代表车辆，代表车辆车长23.2 m，轴重14.95 t。列车采用6 节编组，首尾两节机车，中间四节拖车。

车辆空间振动分析模型如图2 所示，分析中采用以下假定：

图2 车辆空间振动分析模型示意图

（1）车体、转向架和轮对均假设为刚体。

（2）不考虑机车、车辆纵向振动及其对桥梁振动与行车速度的影响。

（3）轮对、转向架和车体均作微振动。

（4）所有弹簧均为线性，所有阻尼按粘滞阻尼计算，蠕滑力按线性计算。

（5）沿铅垂方向，轮对与钢轨密贴，即轮对与钢轨的竖向位移相同。

车辆由车体、转向架、轮对3 部分组成，每部分均假设为刚体，各部分之间通过弹簧和阻尼器相连。

2.1.2 桥梁模型

以上海市轨道交通蕴藻浜桥为原型桥进行研究，该桥全长110 m，桥宽12.5 m，主桥由钢管混凝土拱肋，预应力混凝土横梁与系梁及整体化桥面系组成。主拱横向中心距为11 m，桥面宽9.6 m，横向布置双线轨道交通。

采用杆、梁、板、体等多种单元类型，借助空间有限元软件ANSYS 建立该桥有限元模型如图3 所示。

图3 桥梁有限元模型

经计算，桥梁基频为0.621 Hz，前2 阶阵型分别为拱肋对称横弯和拱肋反对称横弯，第三阶阵型为主梁反对称竖弯。经ANSYS 计算桥梁模态信息，作为计算车桥耦合动力响应的基础。

2.1.3 轨道不平顺

根据同济大学道路与交通工程教育部重点实验室李再帏[7]等的研究，城市轨道交通轨道不平顺谱和德国铁路低干扰谱水平相当，优于美国6 级轨道谱、德国铁路高干扰谱和中国提速干线谱。因此该文基于德国铁路低干扰谱函数，模拟得到的轨道随机不平顺样本（500 m）如图4 所示。

图4 随机轨道不平顺样本

车桥耦合振动计算中，荷载采用单线列车过桥（以定员载重情况下的地铁A 型车作为代表车辆，代表车辆车长23.2 m，轴重14.95 t，列车采用6 节编组，首尾两节机车，中间四节拖车），车速v=80 km/h。

2.1.4 计算工况简述

该文选取的动力响应指标包括相应断杆下桥面的动位移峰值、速度峰值、动应力峰值和加速度变化率峰值，并对比研究了不同梁拱刚度比，各吊杆损伤及多吊杆损伤的工况下，各动力响应指标的敏感程度。图5~6 为位置点标识和吊杆编号示意图以及吊杆损伤模拟示意图。

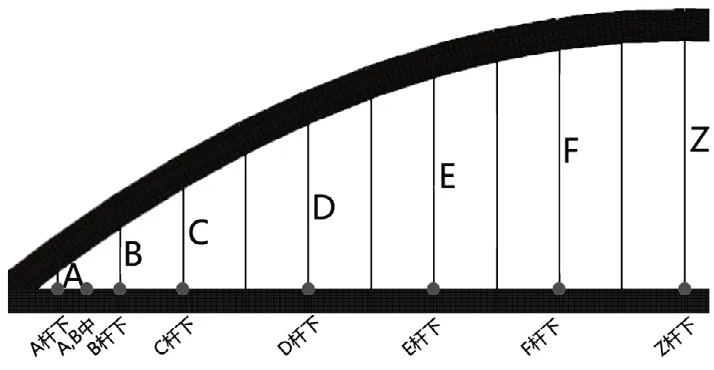
图5 位置点标识和吊杆编号示意图

2.2 基于动位移峰值的损伤识别研究

为研究吊杆损伤对相应桥面动位移峰值的敏感性，计算了以下4 种工况：

（1）A 杆、B 杆断裂，观察列车经过时A 杆下、B 杆下以及A、B 杆中的桥面动位移峰值。

（2）降低主梁刚度（弹性模量降低50%），A 杆、B 杆断裂，观察A 杆下、B 杆下以及A、B 杆中的动位移峰值。

（3）为与长吊杆损伤做对比分析，补充计算了列车经过时，C 吊杆、D 吊杆、E 吊杆、F 吊杆、Z 吊杆损伤工况的动位移峰值。

（4）依次增加断杆根数（如图6 所示），直到动位移峰值呈现出显著差异。

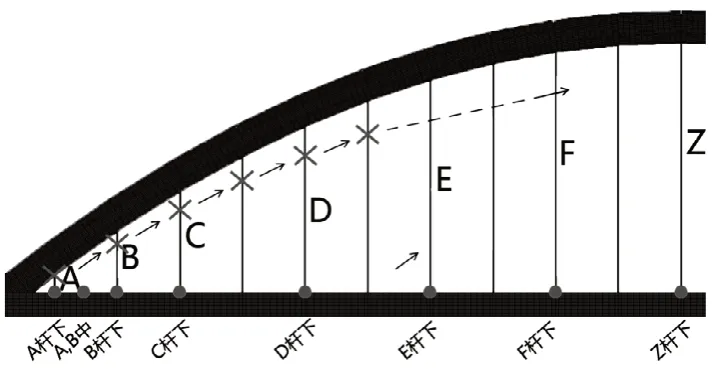
图6 依次增加断杆根数示意图

计算结果整理见图7~10。

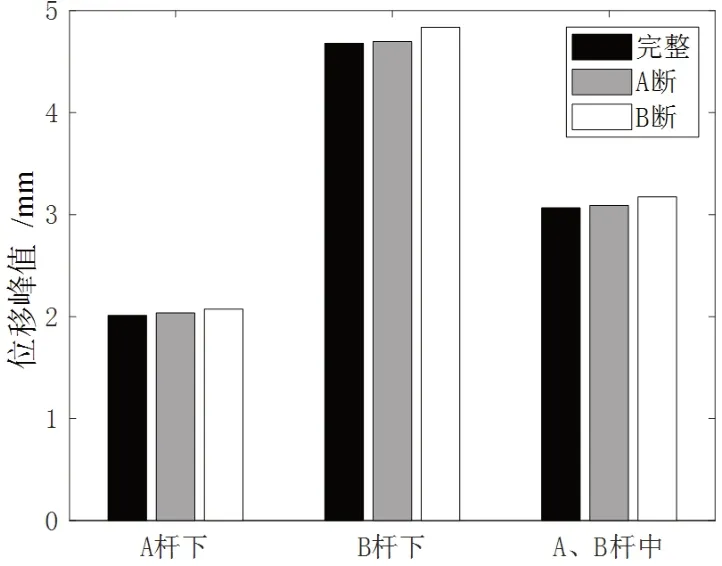
图7 动位移峰值（短吊杆损伤）

图8 动位移峰值（降低梁拱刚度比）

图9 动位移峰值（增加长吊杆损伤）

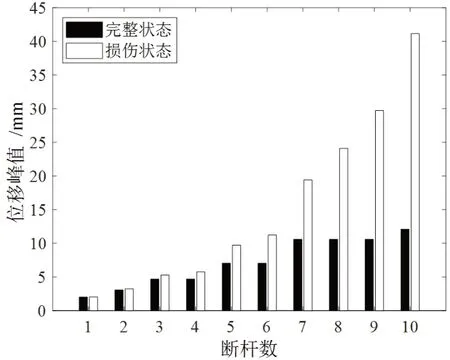
图10 动位移峰值（增加吊杆损伤根数）

从图7~10 可以看出，短吊杆损伤对其相应桥面的动位移峰值敏感性较弱。降低梁拱刚度比不能提高其敏感性。随着损伤吊杆长度的增加，动位移峰值差值逐渐变大，但最大差值百分比不超过8%，长吊杆损伤对动位移峰值的敏感性仍然较弱。随着损伤吊杆根数的增加，动位移峰值的差值百分比急剧增大，最大可达约300%。

2.3 基于加速度峰值的损伤识别研究

基于加速度峰值的损伤识别计算工况同上。计算结果整理见图11~14。

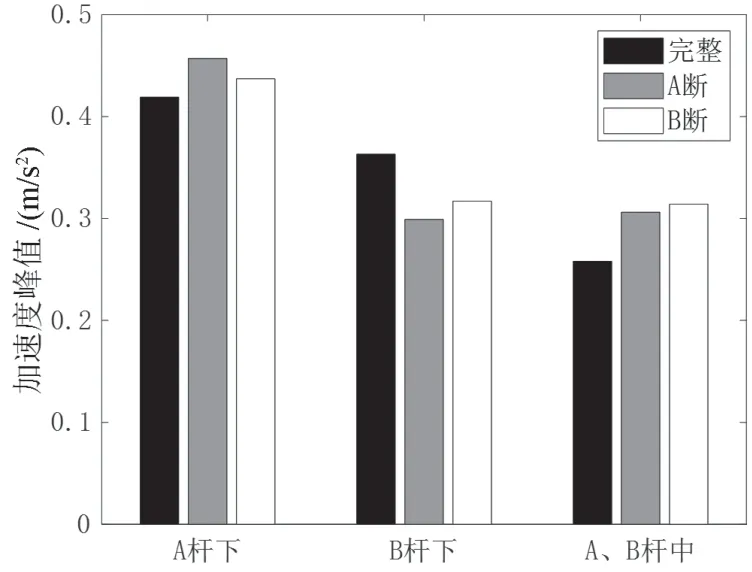
图11 加速度峰值（短吊杆损伤）

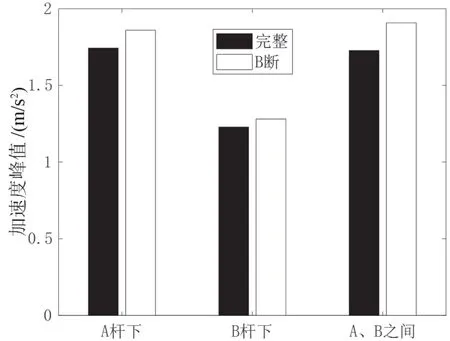
图12 加速度峰值（降低梁拱刚度比）

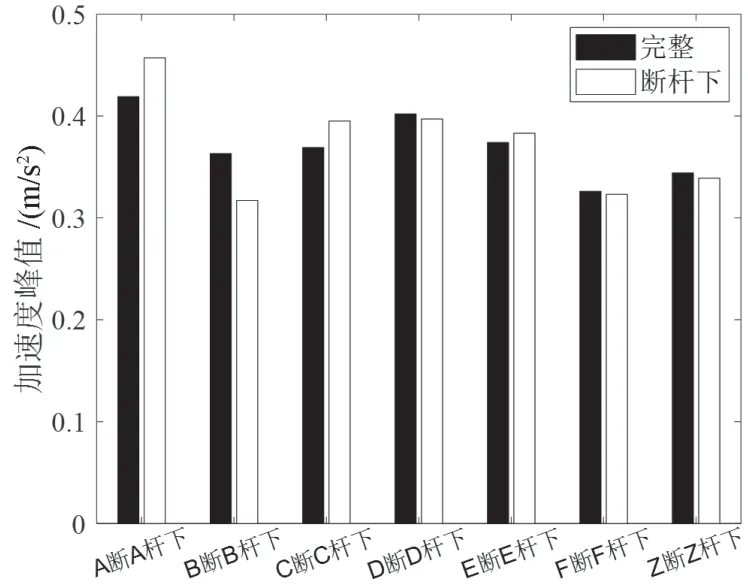
图13 加速度峰值（增加长吊杆损伤）

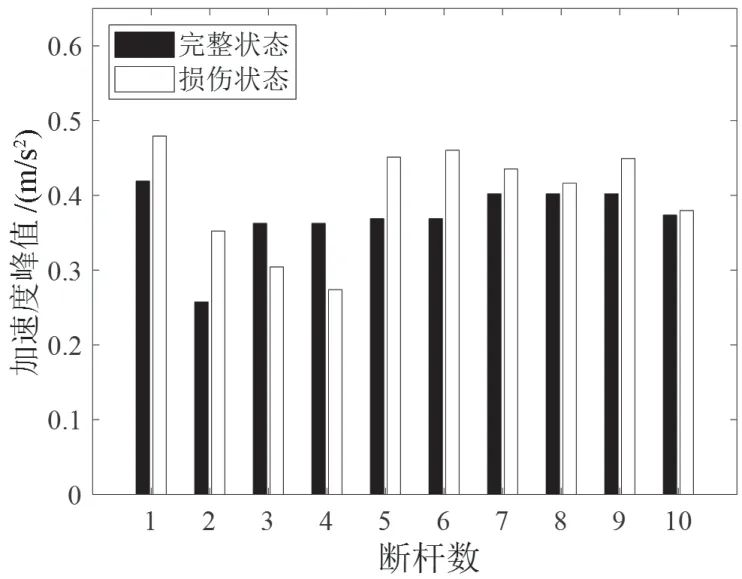
图14 加速度峰值（增加吊杆损伤根数）

从图11~14 可以看出，短吊杆损伤对其相应桥面的加速度峰值敏感性较弱，但略强于动位移峰值的敏感性。降低梁拱刚度比、增加损伤吊杆长度或增加损伤吊杆根数，均不能提高吊杆损伤对加速度峰值的敏感性。加速度峰值对于吊杆损伤是一个不敏感指标。

2.4 基于动应力峰值的损伤识别研究

基于动应力峰值的损伤识别计算工况同上。计算结果整理见图15~18。

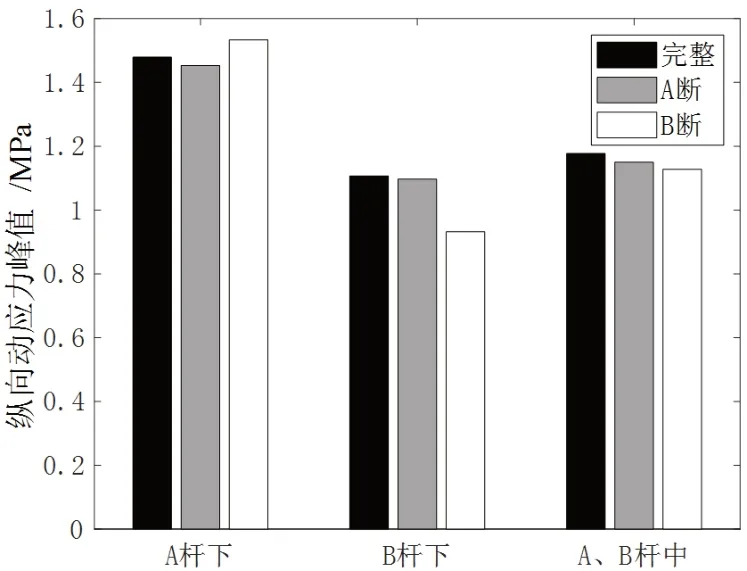
图15 动应力峰值（短吊杆损伤）

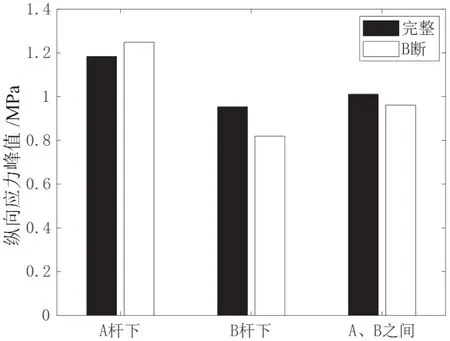
图16 动应力峰值（降低梁拱刚度比）

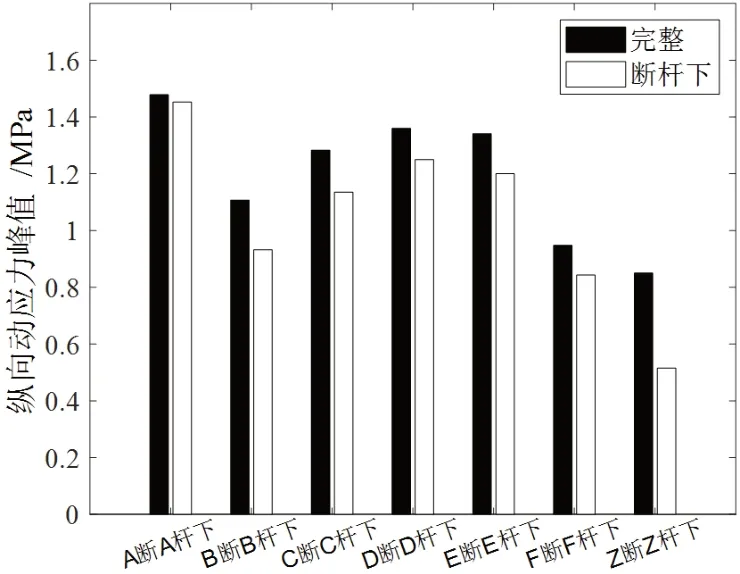
图17 动应力峰值（增加长吊杆损伤）

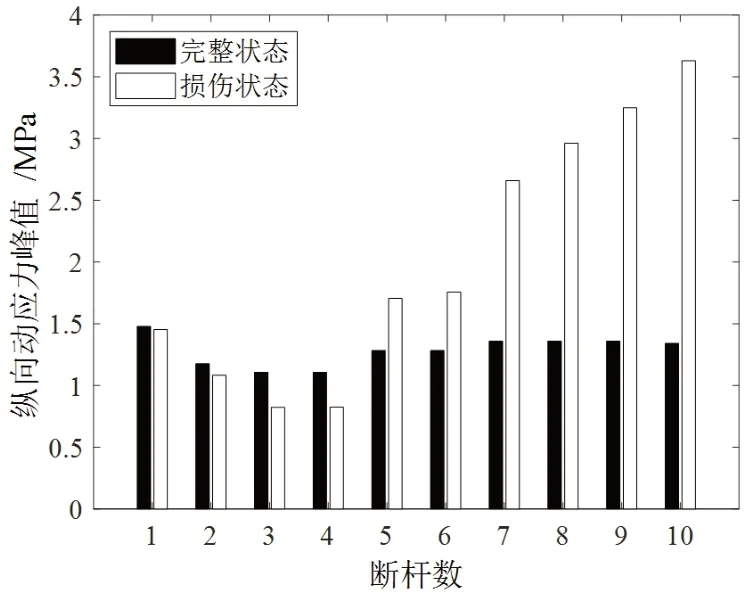
图18 动应力度峰值（增加吊杆损伤根数）

从图15~18 可以看出，短吊杆损伤对其相应桥面的动应力峰值敏感性较弱。降低梁拱刚度比不能提高其敏感性。随着损伤吊杆长度的增加，动应力峰值差值逐渐变大，最大差值百分比可达40%，长吊杆损伤对动应力峰值的敏感性相对较强。随着损伤吊杆根数的增加，动应力峰值的差值百分比急剧增大，最大可达约260%。

2.5 基于加速度变化率的损伤识别研究

为了寻找更敏感的动力指标，提出了加速度变化率（Δa/ΔT）。研究计算工况同上。其计算结果表明，加速度变化率峰值的响应变化规律与加速度峰值基本一致，因此在这里不再展示其计算结果，其响应变化规律可参考2.3节中加速度峰值的变化规律。

3 结论

（1）对于短吊杆损伤，动位移峰值、加速度峰值、动应力峰值以及加速度变化率峰值等动力响应指标均不具备良好的敏感性，和完整状态对比，对应断杆下桥面的动力指标差值均在10%以内，调整梁拱刚度比亦不能提高其敏感性。

（2）加速度峰值和加速度变化率的响应规律基本一致，对于吊杆损伤属于不敏感指标。

（3）随着损伤吊杆长度的增加，与桥梁完整状态对比结果表明，列车经过时动位移峰值的差异越来越显著，但最大差值百分比不超过8%；而动应力峰值差异显著增大，最大差值百分比可达40%。因此可以认为，动应力峰值可以为系杆拱桥长吊杆的损伤识别提供参考。

（4）随着损伤吊杆根数的增加，与桥梁完整状态对比结果表明，列车经过时动位移与动应力峰值的差异越来越显著，最大差值百分比分别可达300%和260%，因此可以认为动位移峰值与动应力峰值的变化可为系杆拱桥多吊杆损伤提供较大的参考价值。