非饱和状态下交通信号控制优化方法研究

余炳杰

（广州市交通规划研究院有限公司,广东 广州 510030）

0 引言

随着城市化进程的加快，大量人口向城市聚集，道路交通拥堵现象严重。目前，缓解城市交通拥堵的措施有两种：一是增加城市交通道路规模，二是在现有道路资源的基础上，利用先进的技术和理念管理城市交通信号，降低车辆延误时间，提高道路通行能力。措施一会受到城市占地的限制，且造价较高，措施二投入的资金少，因此，进一步研究交通信号控制优化方法十分重要。

1 交叉口的交通状态控制基本理论

1.1 交通状态分类

城市道路交叉口有十字形、X 形、T 形、Y 形等，交通流量较大。如果交叉口无交通控制信号，其冲突点数量随相交叉道路数量快速增加，两者之间满足式（1）[1]：

式中，n—交叉口相交叉道路数量（条）。

按饱和度不同，可将城市道路交叉口的交通状态划分为非饱和（饱和度＜1，供给大于需求）、饱和（饱和度=1，供给等于需求）、过饱和（饱和度＞1，供给小于需求）三类。对于大型或特大型城市，道路网密集，大部分时间处于饱和、过饱和状态，而对于中小型城市，道路网较稀疏，除个别高峰时段，交叉口多处于非饱和状态。当交叉口交通状态处于饱和或过饱和时，道路可能出现“溢流”现象，仅仅依靠优化交通信号控制方案无法缓解交通拥堵状态；当交叉口处于非饱和状态，优化交通信号控制方案能提高交通运行效率，降低车辆延误、停车次数等。

1.2 交通控制方法

1.2.1 交通控制方法分类

交叉口是城市路网的重要组成部分，也是交通拥堵和交通安全事故的多发地，故对交叉口进行信号控制，提高其通行能力十分必要。按控制对象和范围不同，可将交叉口信号控制方法分为单交叉口控制、干线协调信号控制、区域协调信号控制。单交叉口控制是只以某个交叉口为控制单位，是最简单的信号控制方法，其配时参数是信号周期和绿信比。但在实际工程中，不同交叉口之间具有明显的时空关联性，即某个交叉口交通状态改变后，与之相邻的其他交叉口的交通状态也会受影响，进而影响信号配时方案。在此情况下，采用干线或区域协调信号控制效果更好，其配时参数主要是信号周期、绿信比和相位差[2]。

1.2.2 配时参数分析

信号周期：用于指挥交叉口交通的信号是循环变化的，一个循环由若干个步组成，各步的步长为信号子周期。假如一个循环有n步，一个信号周期等于n步步长。

绿信比：在一个信号周期内，某相位的有效绿灯时间与周期长度之比称为绿信比。绿信比可以表达该相位交通流在一个周期中需要的绿时。绿信比经优化后，能将绿时合理分配给各相位的交通流，以缓解交叉口的拥堵问题。

相位差：相位差只用于干线或区域协调信号控制中，即以干线或区域内的某一交叉口作为基准交叉口，其他各交叉口的协调相位起始时刻滞后于基准交叉口的协调相位起始时刻的最小时间差就是绝对相位差。

2 交叉口的交通状态信号控制模型优化

2.1 单点信号控制优化

早期在研究交叉口信号配时参数时，大部分是针对单一指标，这样可能出现部分指标优化，而其他指标反而下降的问题。为了解决这一问题，交叉口的信号控制宜采用多目标优化模型。

2.1.1 优化目标选取

该文主要针对非饱和状态下的交通流进行研究，此时人为车辆的到达与驶离保持动态平衡，可不考虑上游交叉口的信号配时对下游交叉口的影响。结合相关研究成果，选择交叉口通行能力、周期延误、停车次数、尾气排放四个性能目标构建信号控制优化模型，对各优化目标赋予相应的权重系数，具体计算公式见表1[3]。

表1 道路交叉口优化目标计算

考虑道路交叉口的交通运营总体效率，分别以通行能力最大、总延误时间最小、总停车次数最小、尾气排放最小为目标建立优化模型，分别记作Z1=min(Cap)、Z2=min(D)、Z3=min(M)、Z4=min(E)。

2.1.2 模型求解

在约束条件固定的前提下，基于“模糊折中规划思想”地将多目标优化模型转换为单目标优化模型，寻找与理想解距离最小的解，以优化交叉口的信号周期和绿灯时长，具体计算步骤如下：计算各目标函数的隶属度函数uzi→计算第i个目标函数的权重λi→构建关系矩阵→将多目标函数转化为单目标函数Z，见式（2）[4]：

式中：p—距离指数，一般取1、2、∞。

2.1.3 模型验证

以某城市典型的十字交叉口为研究对象，利用上述模型对其交通信号控制方案进行优化，并与其他模型的优化结果进行对比。该交叉口为四相位配时，如图1 所示[5]。

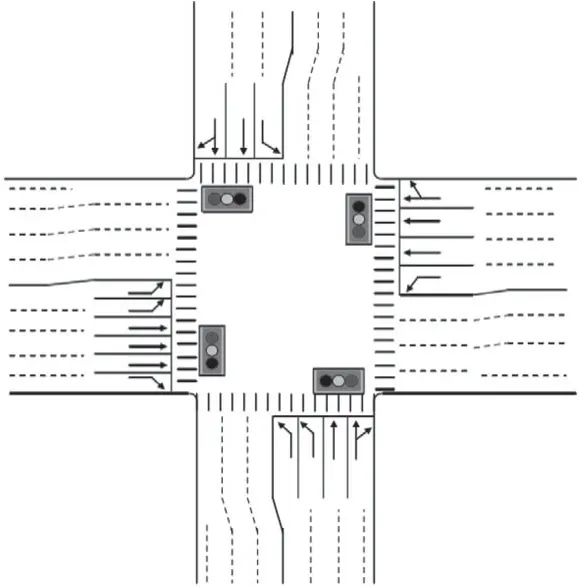
图1 平面交叉口信号配时示意

为了便于计算，将东西向直行车流、东西向左转车流、南北向直行车流、南北向左转车辆所在的相位分别命名为1、2、3、4。经现场调查，左转车道、直行车道、右转车道、直右混行车道的饱和流量分别为1 800 pcu/h、1 900 pcu/h、1 600 pcu/h、1 800 pcu/h。

随后，将模糊折中规划法的计算结果与其他方法的计算结果进行对比，见表2。

表2 交叉口交通运行效益对比

由表2 可知：①相对于方案二，方案一的周期延误减小了7.01%，通过车辆数增加了2.85%，平均停车数减少了2.3%，总停车数减少了3.5%；②相对于方案三，方案一的周期延误减小了9.6%，通过车辆数增加了1.2%，平均停车数减少了4.6%，总停车数减少了6.2%。上述现象表明，模糊折中规划法对交叉口周期延误的优化效果最好，通过车辆数的优化效果最差。

2.2 干线协调信号控制优化

干线协调信号控制优化的目标是协调某一主路上各个交叉口的信号周期、绿信比、绝对相位差等参数，确保尽可能多的车辆连续通过。相对于单个交叉口信号控制，干线协调信号控制能大幅提高道路通行效率，降低主路上的车辆延误时间、停车次数、尾气排放量等[6]。

2.2.1 优化方法

最大绿波带法控制模型所需参数少，计算简单，但得到的绿波带以对称于中心线为主，使得部分绿灯时间浪费；最小延误法是建立车辆延误时间与绝对相位差的函数关系，目标函数最小时对应的信号配时参数最优，但并未考虑上下游交叉口车辆的到达和消散。针对上述问题，该文构建了改进的MULTIBAND 模型，增加绿波带的左右带宽约束条件，并基于道路上下游车辆的排队特性构建了车辆排队消散时间模型，以更好地优化绿波带形式及干线上多个交叉口的信号配时。

2.2.2 模型验证

为了验证上述优化模型的有效性，取某一城市主干路为研究对象。该主干路为南北走向，沿线有4 个十字形交叉口，第1 个和第2 个交叉口的间距为566 m、第2个和第3 个交叉口的间距为654 m、第3 个和第4 个交叉口的间距为720 m，不同交叉口均采用四相位配时方案，如图2 所示[7]。

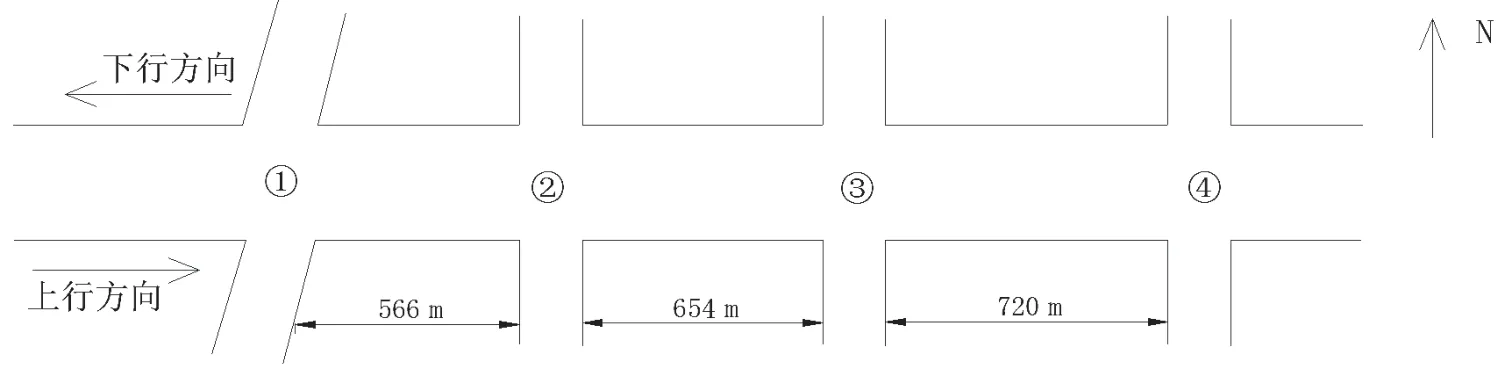
图2 干线交叉口组合示意

以平均延误和平均停车次数为评价指标，对比了不同行车方向的信号控制效果，见表3。

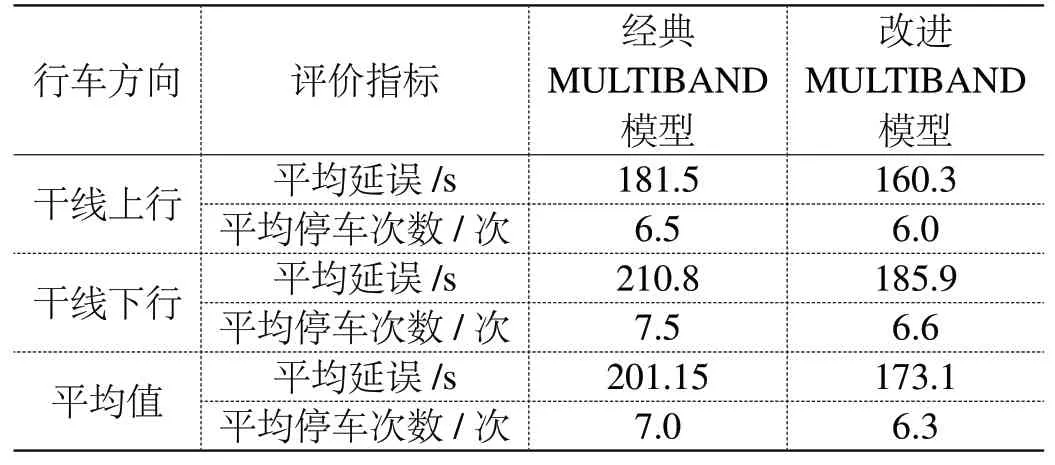
表3 干线协调信号控制效果对比

由表3 可知：MULTIBAND 模型改进后，干线上行方向的平均延误减少了21.2 s，减小幅度为11.7%，平均停车次数减小了0.5 次，减小幅度为7.7%；干线下行方向的平均延误减少了24.9 s，减小幅度为11.8%，平均停车次数减小了0.9 次，减小幅度为12.0%。这表明改进的MULTIBAND 模型能明显改善减缓道路的拥堵，并提高其通行能力。

2.3 区域协调信号控制优化

当城市路网的部分道路因交通拥堵而导致车辆滞留，而其他道路未被充分利用，会导致交通资源浪费。因此，需将路网划分为若干个子区域，并结合子区域的交通特性制定信号控制方案，以有效提高路网的整体通行能力[8]。

2.3.1 子区域划分

为了提高城市路网子区域划分水平，应坚持以下原则：一是距离原则。相邻交叉口之间的距离直接决定了车辆的驶出特性和到达特性。如果相邻交叉口间距离长，上游交叉口驶出车流有明显的离散现象，降低了信号协调控制的必要性。反之，上游交叉口驶出车流能连续地到达下游交叉口，信号协调控制十分必要；二是流量原则。区域路网的复杂性受交通流量影响较大，比如相邻交叉口之间的车流量差不多，则认为相关性强，可将其划分在同一子区域内；三是周期原则。如果相邻交叉口的周期时长接近，则认为相关性强，可将其划分在同一子区域内。

2.3.2 双层规划模型

结合相关研究成果，该文提出了双层规划模型来优化路网区域控制方案。双层规划模型由一个上层模型和多个下层模型组成，上、下层模型都有自己的目标函数。上层模型应以子区域通行能力最大为优化目标，以公共周期时长为决策变量。而在交叉口信号配时设计时，各相位绿灯时长直接影响公共信号周期，故下层规划模型主要对各交叉口的有效绿灯时长优化[9]。

2.3.3 模型验证

为了验证双层优化模型在区域信号协调控制中的可行性，将某城市开发区路网（2 条主干路，6 条支路）划分为两个子区域，命名为子区A 和子区B，其中子区A包括交叉口①②③④，子区B 包括交叉口⑤⑥⑦⑧⑨，如图3 所示。

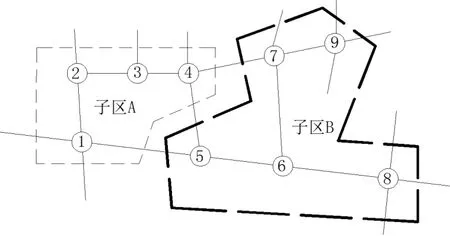
图3 城市路网子区域划分

将仿真参数（仿真时长1 h，输出时间间隔为10 min，共6 个输出间隔）输入到VISSIM 软件中，利用双层优化模型计算了子区A 和子区B 的平均延误，计算结果见图4。

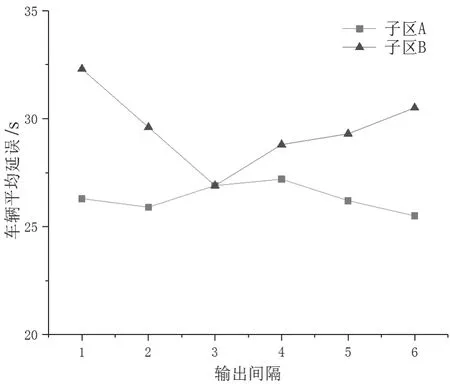
图4 子区域交通信号控制结果

由图4 可知：经双层规划模型优化后，子区A 的平均延误为26.8 s，子区B 的平均延误为30.9 s。同时，在任意输出间隔下，子区B 的平均延误均大于子区A。

4 结语

该文主要分析了城市交叉口的交通状态，并基于先进的设计理念，系统性地阐述了交通控制方法，得到了以下几个结论：

（1）城市道路交叉口交通可划分为非饱和、饱和、过饱和状态，其中非饱和状态采用信号控制效果更好。

（2）交叉口单点信号控制可基于“模糊折中规划思想”，将多目标优化模型转换为单目标优化模型，并以通行能力最大、总延误时间最小、总停车次数最小、尾气排放最小为优化目标。

（3）干线协调信号控制建议采用最大绿波带法，并使用改进的MULTIBAND 模型优化绿波带形式。

（4）区域协调信号控制的关键是基于距离原则、流量原则、周期原则划分子区域，并利用双层规划模型来优化路网信号控制方案。