基于综合因素的风力发电资源评估研究
徐 汉
(中国能源建设集团广东省电力设计研究院有限公司)
0 引言
风力发电资源评估,是指对某一特定区域内的风能资源进行评估,以确定其可利用性和开发潜力的过程。风力资源评估的主要目的是为风力发电项目的决策而制定的,为风电场布局和风电机组选型提供可靠的基础数据和技术支持[1]。同时还能为环保、节能和社会责任等方面提供重要支持。通过科学合理的风力发电资源评估与分析,可以实现对该区域风能资源的最大化利用,推动可再生能源的发展与应用。
风力资源评估包括风荷载密度和风功率密度的估计,两者对于风电场的建设同样重要。风荷载密度有助于评估风机塔筒和风机叶片的疲劳失效[2]。自然气流会导致细长结构的疲劳破坏,这是由于周期性的涡旋脱落造成的。如果周期性旋涡脱落的频率与结构的固有频率相匹配,则明显的侧风振动将对结构以及风机叶片造成破坏[3]。风力密度有助于将风的动能转化为电能。它有助于选择建设风力发电场的潜在地点,并在给定地点选择合适的风力发电机。因此,正确评估风能的这两个方面是非常重要的。在文献中,双参数韦伯分布一直是描述风力资源状态的最被广泛接受且被推荐的模型之一。韦伯分布的一个特别显著的特征是,如果风速在形状参数k和尺度参数s下遵循韦伯分布,负荷和功率密度也分别在形状参数k/2和k/3以及尺度参数s2和s3下遵循相同的分布。
除了风速之外,风向的评估对于在给定地点利用风能潜力也同样重要。首先,它有助于为风电场的安装位置建立一个理想的区域;其次,它对架空输电线的安装有重大影响。因此,如果不进行风向的分析,研究某一特定地点的风能是徒劳的[4-5]。风向分析需要使用特殊的统计模型,即圆上的分布。事实上,平面上所有的观测值都可以认为长度为1,并且位于同一个圆上。
1 理论分析
在本文中,我们提出两个主要目标。本文提出了一种新的修正能量模式因子(MEPF)方法来估计双参数韦伯分布的参数。该MEPF方法的优点是它不需要求解最小二乘问题,也不需要进行迭代计算。本文将MEPF算法与前人研究的算法的性能进行了比较。这种比较将基于固定数值的100~100000个不同样本量的模拟数据。
1.1 韦伯参数模型
韦伯分布是一种灵活的分布,广泛用于描述单峰频率分布,如特定位置的风场。概率密度函数f(v)和累积分布函数F(v)分别由下式表示。
式中,v>0,k>0,s>0,其中v为参考风速,k为无量纲参数,s为与v维数重合的尺度参数。
风机的轮毂大多位于大气边界层的表层区域。在这个区域内,风速随着高度的增加而急剧增加。利用简单的幂指数或对数可以估计垂直风切变廓线。利用幂指数可外推不同垂直高度韦伯分布的尺度参数s。该幂指数中使用的赫尔曼指数α是给定位置粗糙度的函数。下式给出了确定韦伯分布和垂直风廓线的赫尔曼指数α、形状参数k和尺度参数s的表达式。
其中,za是风速测量计高度,sa、ka分别是风速测量计高度的尺度参数、形状参数和平均风速,zref是参考高度,z是估计韦伯参数的高度。
1.2 风力发电机容量系数
容量系数(Capacity Factor,CF)是指给定时期内总发电量与同期总额定发电量之比。此系数用以检测哪个地点最适合安装风力发电机。导出的容量系数基本方程的表达式如下:
其中,Vr为额定风速,Vc和Vf分别为切入风速和切出风速,f(v)代表韦伯密度函数。
Vr/s被称为归一化额定风速。归一化额定风速从0.1到4不等,并对应在横坐标上,而相应的容量因子绘制在坐标上的形状参数的不同值(k=1.0~3.0),最大容量系数点在x轴上的投影是用来评价风机设计额定风速的点。因此,可以得出结论,风机的额定风速应在该高度韦伯分布标度参数的0.5~1倍的范围内,以实现最大容量因数。容量系数与风速关系如图1所示。

图1 容量系数与风速关系
1.3 韦伯分布的随机变量生成
为了说明如何按照指定的韦伯分布生成随机变量,样本量从100到100000不等,以10的倍数为单位。为了模拟风速,生成了一个韦伯分布,其形状参数k从1到4不等,步长为0.5,比例参数从2到15不等,步长为1。这些韦伯参数被称为真韦伯参数,本文运用不同的方法进行仿真。下式给出了用这种韦伯分布生成风速数据的方程:
其中,RN是均匀分布在[0,1]上的随机变量,v是目标韦伯随机变量。
1.4 改进的能量模式因子法(MEPF)
基于前人研究所述,Epf是形状参数函数。为了克服此问题并避免PDM(功率密度法)中的不准确性问题,我们采用以下新过程。令k值在1到15之间变化,早期的研究结果表明,选取某一地区风速中,k大于1。我们以Epf比值为横坐标,k为纵坐标。利用曲线拟合技术模拟Epf与k的变化。用于拟合k和Epf之间变化的三个不同的理性函数为M1、M2和M3,k与Epf的图形和函数f(∞)趋向水平。研究结果表明,MEPF是最合适的函数。图2显示了拟合有理函数MEPF的图形表示。因此,可以得出结论MEPF可以用来模拟k与Epf的变化。

图2 K与Epf的变化及最佳拟合函数
2 实验及分析
为验证MEPF方法模拟韦伯分布的数据有效性,本文运用形状和尺度参数的真实值为参考,并将估算值与这些真实值进行比较。因此,本文已经考虑了样本量在100~100000之间变化的各种仿真场景。在每种情况下,使用七种不同方法,即最小二乘法或图解法(LSM)、经验方法(EM)、矩量法(MOM)、最大相似法(MLM)、改进的最大相似法(MMLM)、功率密度法(PDM)和改进的能量模式因子法(MEPF)估计韦伯参数,并将估计值与模拟数据中的真韦伯参数进行比较,形状参数的不同值会对韦伯分布的形状产生明显的影响。形状参数k决定了韦伯分布的性质。因此,本文选择它作为横坐标,对不同的方法进行仿真比较。
图3显示了七种不同的方法下基于不同样本量估计韦伯形状参数与真实韦伯形状参数之比。由此可得,对于样本量n=100和k=1,LSM方法低估了真实形状参数,而PDM高估了真实韦伯参数,随后是MEPF、EM和MOM。随着k的增加,由MEPF、MOM和EM估计的韦伯参数逐渐逼近真实韦伯参数。随着样本容量的增加,LSM和MEPF的性能显著提高,除PDM和EM外,其他方法都能得到较好的估计。当n=100000时,在7种方法中,我们可以看到LSM、MOM、MLE、MMLM 和MEPF表现相同,而PDM表现较差,其次是EM。
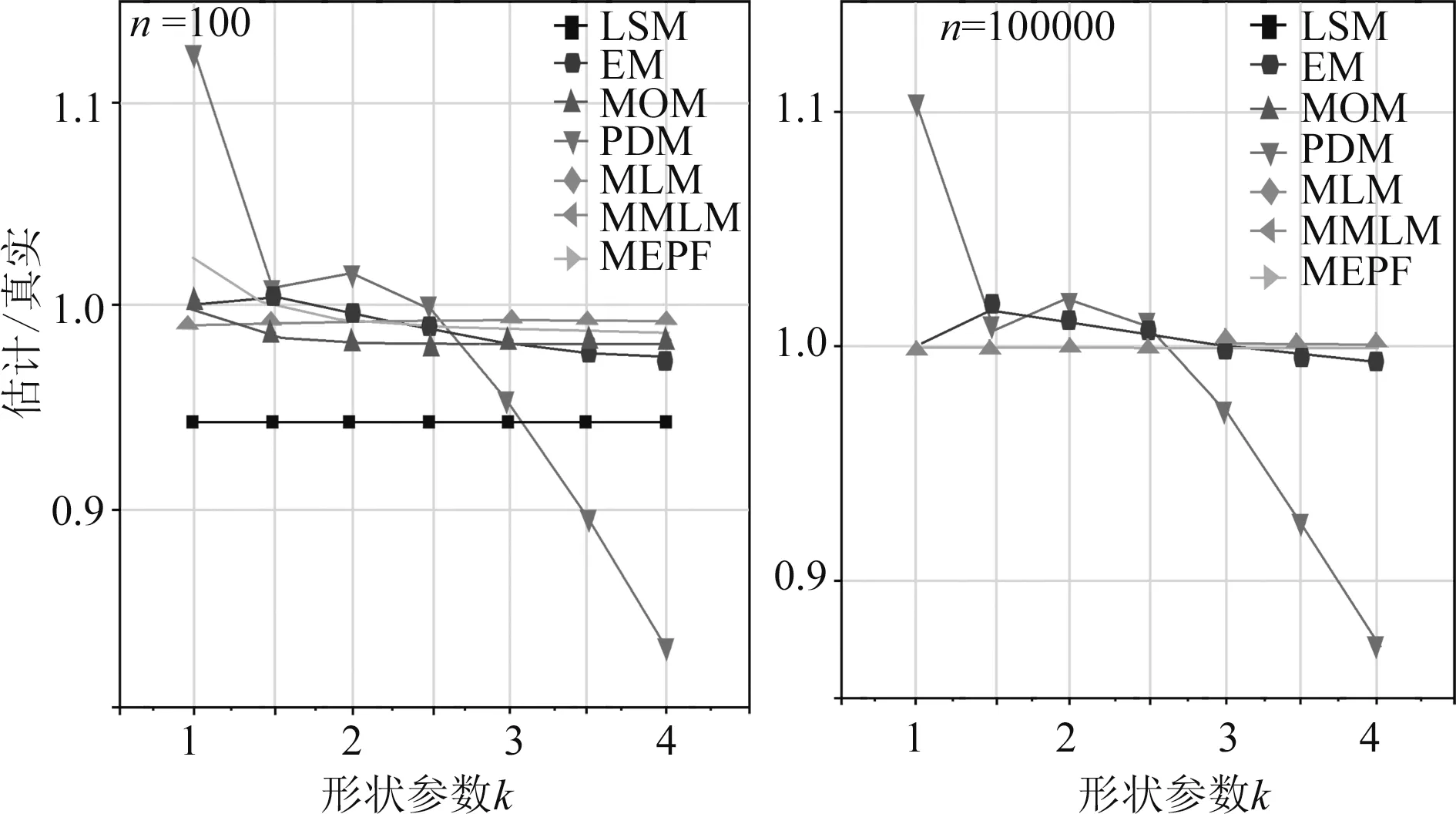
图3 估计形状参数与真实形状参数
图4显示了估计的尺度参数与真实尺度参数的比值。与前面的结论类似,通过分析可得,对于n=100和k=1时,PDM 高估了尺度参数,其次是MEPF和EM,而LSM低估了真实尺度参数。尤为突出的是,在k=1.5~3时,PDM估计值接近真值,而在k=3之后,仍然存在高估。随着n的增加,所有方法的性能都有所提高,尤其LSM的性能有了显著的改善。对于n=100000,MEPF方法表现出与本文讨论的形状参数相似的行为。

图4 估计尺度参数与真实尺度参数
通过上述讨论可知,在样本量足够大的情况下,本文所提出的MEPF在估计韦伯参数方面优于LSM、MOM、MLE和MMLM等方法。对于较小的样本量和较低的k值,MEPF、MOM、MLM和MMLM的性能最好。对于较大样本量PDM的性能不如其他方法,其次是EM。
在这个模拟研究的基础上,我们得出结论,MEPF的性能明显优于PDM算法,它是一个运用竞争性的方法来估计韦伯分布的参数,并且与LSM、MOM、MLE和MMLM 相比,MEPF在估计风电场真实平均功率密度方面具有同样的优势。
3 结束语
本文将提出的修正能量模式因子法与文献中提出的六种不同的韦伯参数估计方法进行了比较。我们的仿真研究表明,MEPF方法是这些方法的一种合适的替代方法,它在精度和简单性方面明显优于其他方法,与其他方法相比,MEPF方法具有鲁棒性强、计算效率高、不存在分类问题和不需要任何复杂计算的优点,如最小二乘法、矩量法和最大似然法。该方法具有较高的参数估计精度,运用MEPF法分析在何处安装风力发电机,在现实中也达到了预期成果。

