非Lipschitz条件下高维McKean-Vlasov随机微分方程解的存在唯一性
马 丽, 孙芳芳
(1. 海南师范大学 数学与统计学院, 海口 571158;2. 海南师范大学 数据科学与智慧教育教育部重点实验室, 海口 571158)
0 引 言
设(Ω, F,P)是完备的概率空间, (Ft)t∈[0,T]是其上一个满足通常条件的σ-代数流.P(d)是(d,B(d))上概率测度组成的集合,P(d)上的拓扑为弱收敛的拓扑.考虑d上McKean-Vlasov随机微分方程(也称为分布依赖的随机微分方程):

(1)
其中,T为正常数,b:[0,T]×d×P(d)→d和σ: [0,T]×d×P(d)→d×d都是Borel可测函数,W(t)是带流的概率空间(Ω, F, (Ft)t∈[0,T],P)上一个d维标准Brown运动,LXt为Xt在时刻t处的边缘分布.对d)是d-值F0-可测的p阶矩有限的随机变量做成的空间.
当系数不依赖于分布和时间且漂移系数b不连续时, 文献[1]考虑了一维随机微分方程, 在漂移系数b逐段Lipschitz连续, 扩散系数σLipschitz连续的条件下, 得到了解的存在唯一性及Euler-Maruyama(EM)数值解.文献[2]考虑了高维随机微分方程,当漂移系数b满足逐段Lipschitz连续,扩散系数σ满足Lipschitz连续时,利用Zvonkin变换消除了漂移系数的不连续性,通过逆变换得到了解的存在唯一性,并对转换后的方程的EM数值解用逆变换,从而得到原来方程的EM数值解及其强收敛的速度.文献[3-5]研究了几类随机微分方程解的渐近性和稳定性等问题.
当b(t,x,μ)和σ(t,x,μ)不依赖于t且关于(x,μ)是Lipschitz连续的,文献[6]得到了方程(1)的强解的存在唯一性,还给出了当系数不是Lipschitz连续时解不唯一的例子.非Lipschitz条件下,McKean-Vlasov随机微分方程解的存在唯一性的研究成果也很丰富.当漂移系数b(x,μ)关于x逐段Lipschitz连续、关于μ是Lipschitz连续,扩散系数σ(x)为Lipschitz连续时,文献[7]得到了一维McKean-Vlasov随机微分方程及其对应的粒子系统解的存在唯一性及EM数值解.当b(t,x,μ)和σ(t,x,μ)关于x可积、关于μ为Lipschitz连续且σ(t,x,μ)非退化时,文献[8]利用Zvonkin变换,通过偏微分方程解的正则性得到了强解和弱解的存在性,再由逐轨道唯一性得到了强解和弱解唯一性.当b(t,x,μ)关于x奇异、关于μ在弱拓扑及全变差距离下可能不连续、被一个分布的线性项与一个关于(t,x)局部可积的项的乘积控制,σ(t,x,μ) 有界非退化且关于(t,μ)为Lipschitz连续时,文献[9]得到了弱解的存在唯一性.当σ(t,x,μ)关于(x,μ)是Lipschitz连续,b(t,x,μ)连续且关于x满足单调条件,b(t,0,μ)关于μ满足增长条件时,文献[10]得到了强解的存在唯一性、指数压缩性和Harnack不等式.当b(t,x,μ)可测有界且关于(x,μ)为Hölder连续,σ(t,x,μ)非退化且关于(x,μ)为Lipschitz连续时, 文献[11]得到了强解的存在唯一性.当b(t,x,μ)由一个局部可积项和一个关于x是超线性增长的、关于μ在带权重的变差距离下是Lipchitz连续的项构成时,σT(t,x)σ(t,x)及其逆矩阵一致有界、关于x是Lipschitz连续时,文献[12]得到了强解的存在唯一性.当σ(t,x,μ)是一致非退化的,b(t,x,μ)满足某些可积性条件且关于μ在全变差距离下连续时,文献[13]得到了弱解的存在性.当系数连续且无界(不一定非退化)时,文献[14]在可积的Lyapunov条件下,得到了定义在多维空间一个区域上的分布依赖的随机微分方程弱解的存在性.从以上文献可知,对高维的McKean-Vlasov随机微分方程,当系数依赖于(t,x,μ)且b(t,x,μ)关于x不连续时,我们需要σ(t,x,μ)是非退化的,从而得到强解的存在唯一性.
本文考虑系数依赖于时间且漂移系数不连续的高维McKean-Vlasov随机微分方程(1),得到了b(t,x,μ)关于x仅仅是逐段Lipschitz连续,σ(t,x,μ)不一定是非退化时,McKean-Vlasov随机微分方程(1)及其对应的交互作用的粒子系统强解的存在唯一性,从而拓展了文献[1-2,7]的结果.特别地,与文献[7]相比,本文考虑的是高维的情形,且σ可以依赖于时间和分布.一维情形下,b(t,x,μ)的不连续集,比较简单,变换函数的逆函数有也显式表达,从而易得逆函数的Lipschitz连续性.高维情形下,变换函数的逆函数不再有显式表达,不连续的区域也更复杂,变换函数及其逆函数的性质不像一维情形那么容易得到.本文借助多元函数的反函数存在定理,得到了该逆函数的存在性及相应的性质,从而得到了变换函数是微分同胚的.
本文主要内容安排如下:第1节,给出了基本的概念、变换函数的定义及性质.第2节,分别证明了漂移系数可分解和不可分解的情况下,McKean-Vlasov随机微分方程及其对应的交互作用的粒子系统解的存在唯一性.第3节为本文的结论.
1 预 备 知 识
1.1 定义和假设
其中,Π(μ,ν)={π:P2(d)×P2(d)→P2(d)|π(μ,ν)(A,d)=μ(A),π(μ,ν)(d,A)=ν(A), ∀A∈B(Rd)}表示测度μ和ν的耦合测度π做成的集合.设Θ是一个正可达的C3超曲面,即存在ε>0,使得p(x)=arg miny∈Θ|x-y|在管状邻域Θε={x∈d|infy∈Θ|x-y|<ε}上是C3单值函数族,且Θ的每个单位外法向量n都有有界的二阶和三阶导数.如果上述ε存在,则称集合{ε|p(x)在Θε上为C3单值函数族}的上确界为Θ的可达距离,记作Reach(Θ),易知p:Θε→Θ且当x∈Θ时p(x)=x.supp(μ)表示μ的支撑.
定义1(文献[2]中definition 3.1、definition 3.2和definition 3.4) 设A⊆d.
1) 对连续的曲线γ:[0,1]→d,定义
称ρ(x,y)=inf{(γ)|γ:[0,1]→A是满足γ(0)=x,γ(1)=y的连续曲线}为A上的内蕴度量.如果不存在从x到y的连续曲线,那么ρ(x,y)=∞.
2) 如果g:A→m是关于A上内蕴度量ρ的Lipschitz函数,即存在常数L>0使得对任意x,y∈A,有
|g(x)-g(y)|≤Lρ(x,y),
则称g是内蕴Lipschitz函数.
3) 设函数g:d→m,如果存在具有有限多个连通部分的超曲面Θ使得g在dΘ上的限制是内蕴Lipschitz函数,则称函数g是逐段Lipschitz函数,称Θ是g的例外集.
假设H1 ①σ,b有界.
②σ(0,0,μ)≠0,且对任意的x,x′∈d,μ,μ′∈P2(d),存在一个常数L1>0使得
‖σ(t,x,μ)-σ(s,x′,μ′)‖HS≤L1(|t-s|+|x-x′|+W2(μ,μ′)),
其中,‖·‖HS为Hilbert-Schmidt范数.
③ 漂移系数b(t,x,μ):[0,T]×d×P2(d)→d关于x为逐段Lipschitz连续的,且b(t,·,μ)的例外集Θ是正可达的C3超曲面.
④ 非平行条件:存在一个常数c0>0,使得对任意的η∈Θ有‖σT(t,η,μ)n(η)‖HS≥c0.
⑤ 对任意的t∈[0,T],η∈Θ,μ∈P2(d),有
(2)
关于η属于C3,其关于η的一、二、三阶导数均是有界的且一阶导数关于t为Lipschitz连续的、二阶导数关于(t,μ)为Lipschitz连续的.
1.2 变换函数G的性质
设L2(Ω,F,P;d)是完备的概率空间(Ω,F,P)上所有二阶矩有限的d-值随机变量做成的空间,其上的标准内积和范数分别为〈·,·〉L2和‖·‖L2.设f:P2(d)→d,X∈L2(Ω,F,P;d),定义称为函数f的提升函数.如果L2(Ω,F,P;d)中存在分布为μ0的随机变量X0,使得提升函数在X0处Fréchet可微,则称函数f在μ0∈P2(d)处L-可微.如果函数f在任意的μ0∈P2(d)处L-可微, 则称f是L-可微函数.由Riesz表示定理可知, 存在(P-a.s.)唯一的Φ∈L2(Ω,F,P;d), 使得当‖X-X0‖L2→0时,有
由文献[15]中proposition 5.25知,存在Borel可测函数χ:d→d,使得Φ=χ(X0),因此
f(LX)=f(LX0)+E〈χ(X0),X-X0〉+o(‖X-X0‖L2).
定义f在μ0处的L-导数为∂μf(μ0)(y)=χ(y),y∈d.对固定的y∈d,如果映射P2(d)μ∂μf(μ)(y)存在一个L-可微的版本, 并且该版本的L-导数连续, 那么对于任意的(μ,y,y′)∈P2(d)×d×d, 定义 ∂μf(·)(y):P2(d)→d的L- 导数为
定义2 设函数f:P2(d)→d.
1) 如果f是L-可微的且其L-导数连续,对任意的μ,映射dy∂μf(μ)(y)存在一个连续的版本,且当y∈supp(μ)时,导数
∂μf(μ)(y), ∂y{∂μf(μ)(·)}(y)
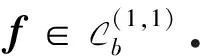
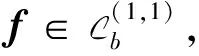
假设H2 假设H1①、H1②成立,且
① 对任意的x∈dΘ,μ,ν∈P2(d),存在常数L2,L3>0使得
此外,对任意的μ∈P2(d),映射dxb(t,x,μ) 在dΘ上逐段Lipschitz连续且Lipschitz常数不依赖于分布μ.
|∂y∂μα(t,y,μ)(y)-∂y∂μα(t,y,ν)(y′)|≤L4(|y-y′|+W2(ν,μ)).
|∂tα(t,η,μ)-∂sα(s,η′,ν)|≤L5(|t-s|+|η-η′|+W2(μ,ν)),
即∂tα(t,η,μ)关于(t,η,μ)是Lipschitz连续函数.此外,∂tα(t,η,μ)是有界的.
设0<ε0
(3)
其中
设idA为集合A上的恒等映射.因为Θ是C3超平面,由文献[2]中remark 3.16知,存在0<ε<ε0使得若η∈Θ,y1∈且|y1|≤ε,则idτη+y1n(η)可逆,其中τη是Θ中η的切空间.
设0 J(y1,…,yd)=y1n(ψ(y2,…,yd))+ψ(y2,…,yd). (4) 引理1 若假设H1、H2成立,0 |∂xG(t,x,μ)-∂yG(s,y,ν)|≤L(|t-s|+|x-y|+W2(μ,ν)). 证明当x∈dΘc时,G(t,x,μ)≡x, 从而∂xG(t,x,μ)关于(t,x,μ)是Lipschitz连续的.下面讨论x∈Θc的情形. |∂xG(t,x,μ)-∂xG(t,x,ν)|= ∂xα(t,p(x),ν)|≤C2W2(μ,ν), |∂xG(t,x,μ)-∂xG(s,x,μ)|= ∂xα(s,p(x),μ)|≤C3|t-s|. 因此 |∂xG(t,x,μ)-∂yG(s,y,ν)|≤ |∂xG(t,x,μ)-∂yG(t,y,μ)|+|∂yG(t,y,μ)-∂yG(t,y,ν)|+ |∂yG(t,y,ν)-∂yG(s,y,ν)|≤ C1|x-y|+C2W2(μ,ν)+C3|t-s|≤ max(C1,C2,C3)(|t-s|+|x-y|+W2(μ,ν)). 取L=max(C1,C2,C3)即可.证毕. 以教学北师大版小学数学四年级上册“确定位置”这一课为例。某教师设计了一项“问路”游戏,即让一名同学扮演迷路的人,让另外一名同学扮演指路的人。在开展这个游戏的过程中,扮演“迷路人”的同学在问路的时候,没有使用“打扰了”、“请问”等礼貌用语。面对这一问题,教师“小题大做”渗透了德育教育。 □ 定义Zt=G(t,Xt,μt),由假设H2②知 因此,由文献[15]中proposition 5.102可得 dZt=(∂tG(t,Xt,μt)+∂xG(t,Xt,μt)b(t,Xt,μt))dt+∂xG(t,Xt,μt)σ(t,Xt,μt)dWt+ (5) 其中 Z0=G(0,ξ,δξ),X0=ξ, LX0=δξ,μt=LXt,t∈(0,T], Lμt(G(t,G-1(t,Zt,μt),·))(μt), (6) (7) 引理2 假设H2①、H2②成立,对所有的(t,x,μ)∈[0,T]×d×P2(d)→d,dy∂μG(t,x,μ)(y)属于C1(d,d).那么,对所有的(t,x,μ,y)∈[0,T]×d×P2(d)×d,G-1:[0,T]×d×P2(d)→d是L-可微的且其L-导数连续.此外,当d=1时, (8) 证明首先注意到,由假设H2②知G是L-可微的.设X,Y∈L2(Ω,F,P;d),LX=μ,LX+Y=ν.对任意的(t,y)∈[0,T]×d,考虑提升函数类似地,对任意的(t,x)∈[0,T]×d,设和固定(t,y)∈[0,T]×d,设 当‖G-1(t,x,μ)-p(G-1(t,x,μ))‖>c时,∂μG(t,G-1(t,x,μ),μ)=0.当‖G-1(t,x,μ)-p(G-1(t,x,μ))‖≤c时,由假设H2②及∂μG(t,G-1(t,x,μ),μ)+∂xG(t,G-1(t,x,μ),μ)∂μG-1(t,x,μ)=0知 |h|=|G-1(t,y,ν)-G-1(t,y,μ)|≤LW2(ν,μ)≤L‖Y‖L2. (9) 若‖Y‖L2→0,则|h|→0,从而最后一个不等式的右边趋于0,因此,式(8)得证.类似于式(8)可得,当d≠1时,∂μG-1(t,x,μ)(y)=-∂μG(t,G-1(t,x,μ),μ)(y)·[∂xG(t,G-1(t,x,μ),μ)]-1,其中,A-1表示矩阵A的逆矩阵.由假设H2②及y∂μG(t,x,μ)(y)属于C1(d,d)可知G-1:[0,T]×d×P2(d)→d是L-可微的,且其L-导数连续.证毕. □ 引理3 若假设H2①、H2②成立,则对任意的t,s∈[0,T],任意的x,y∈d,μ,ν∈P2(d),存在LG-1使得 |G-1(t,x,μ)-G-1(s,y,ν)|≤LG-1(|t-s|+|x-y|+W2(μ,ν)). 证明当0 可得|∂xG-1(t,x,μ)|<2,所以对任意的x,y∈d,有 |G-1(t,x,μ)-G-1(t,y,μ)|≤2|x-y|. 由∂tG(t,G-1(t,x,μ),μ)+∂xG(t,G-1(t,x,μ),μ)∂tG-1(t,x,μ)=0知 |G-1(t,x,μ)-G-1(s,y,ν)|≤ |G-1(t,x,μ)-G-1(t,x,ν)|+|G-1(t,x,ν)-G-1(t,y,ν)|+|G-1(t,y,ν)-G-1(s,y,ν)|≤ □ 接下来,假设c dXt=b(t,Xt,μt)dt+σ(t,Xt,μt)dW(t), 0≤t≤T,X0=ξ 下面证明随机微分方程(5)的系数是Lipschitz连续的,从而式(5)有唯一强解. 证明由假设H1①、H1②、2>|∂xG(t,x,μ)|>1/2、引理1和引理3可得 |∂xG(t,G-1(t,z,μ),μ)σ(t,G-1(t,z,μ),μ)-∂xG(t,G-1(t,z,μ),μ)σ(t,G-1(t,z,ν),ν)|+ |∂xG(t,G-1(t,z,μ),μ)σ(t,G-1(t,z,ν),ν)-∂xG(t,G-1(t,z,ν),ν)σ(t,G-1(t,z,ν),ν)|≤ |∂xG(t,G-1(t,z,μ),μ)||σ(t,G-1(t,z,μ),μ)-σ(t,G-1(t,z,ν),ν)|+ |∂xG(t,G-1(t,z,μ),μ)-∂xG(t,G-1(t,z,ν),ν)||σ(t,G-1(t,z,ν),ν)|≤ 2L1(|G-1(t,z,μ)-G-1(t,z,ν)|+W2(μ,ν))+ C(C1|G-1(t,z,μ)-G-1(t,z,ν)|+C2W2(μ,ν))≤ 2L1(LG-1W2(μ,ν)+W2(μ,ν))+C(C1LG-1W2(μ,ν)+C2W2(μ,ν))≤CW2(μ,ν). |∂xG(t,G-1(t,z,ν),ν)σ(t,G-1(t,z,ν),ν)- ∂xG(t,G-1(t,z,ν),ν)σ(t,G-1(t,z′,ν),ν)|+ |∂xG(t,G-1(t,z,ν),ν)σ(t,G-1(t,z′,ν),ν)- ∂xG(t,G-1(t,z′,ν),ν)σ(t,G-1(t,z′,ν),ν)|≤ |∂xG(t,G-1(t,z,ν),ν)||σ(t,G-1(t,z,ν),ν)-σ(t,G-1(t,z′,ν),ν)|+ |∂xG(t,G-1(t,z,ν),ν)-∂xG(t,G-1(t,z′,ν),ν)||σ(t,G-1(t,z′,ν),ν)|≤ 2L1|G-1(t,z,ν)-G-1(t,z′,ν)|+CC1|G-1(t,z,ν)-G-1(t,z′,ν)|≤ 2L1LG-1|z-z′|+CC1LG-1|z-z′|≤C|z-z′|. |∂xG(t,G-1(t,z,ν),ν)σ(t,G-1(t,z,ν),ν)- ∂xG(t,G-1(t,z,ν),ν)σ(s,G-1(s,z,ν),ν)|+ |∂xG(t,G-1(t,z,ν),ν)σ(s,G-1(s,z,ν),ν)- ∂xG(s,G-1(s,z,ν),ν)σ(s,G-1(s,z,ν),ν)|≤ |∂xG(t,G-1(t,z,ν),ν)||σ(t,G-1(t,z,ν),ν)-σ(s,G-1(s,z,ν),ν)|+ |∂xG(t,G-1(t,z,ν),ν)-∂xG(s,G-1(s,z,ν),ν)||σ(s,G-1(s,z,ν),ν)|≤ 2L1(|t-s|+|G-1(t,z,ν)-G-1(s,z,ν)|)+ C(C1|G-1(t,z,ν)-G-1(s,z,ν)|+C3|t-s|)≤ 2L1(|t-s|+LG-1|t-s|)+C(C1LG-1|t-s|+C3|t-s|)≤C|t-s|. ∂xG(t,G-1(t,z,ν),ν)b(t,G-1(t,z,ν),ν)+Lν(G(t,G-1(t,z,ν),·))(ν) (10) 是Lipschitz连续函数.首先证明 ∂xG(t,G-1(t,z,ν),ν)b(t,G-1(t,z,ν),ν) (11) 是Lipschitz连续函数.设X为U上一个局部定义的过程,那么在(-ε,ε)×R中存在一个局部定义的过程Y,使得 X=Y1n(ψ(Y2,…,Yd))+ψ(Y2,…,Yd), 即X=J(Y).如果Y是方程dY=β(t,Y,ν)dt+ω(t,Y,ν)dW局部定义的解,则由It公式可得 其中,J′和J″分别表示J的Jacobi和Hesse算子.我们想要J′(Y)ω(t,Y,ν)=σ(t,J(Y),ν),即ω(t,Y,ν)=(J′(Y))-1σ(t,J(Y),ν).为方便起见,记G=J-1.令 下面证明(G′)Te1=n.当ξ∈Θ时,J的Jacobi算子J′为 dY=d(G(X))= b(t,J(0,y2,…,yd)+hn(J(0,y2,…,yd)),ν))= G′(J(0,y2,…,yd))2α(t,J(0,y2,…,yd),ν)(nTσσTn)(t,J(0,y2,…,yd),ν)= G′(J(0,y2,…,yd))2α(t,J(0,y2,…,yd),ν)(ωωT)1,1(t,(0,y2,…,yd),ν). (12) 考虑 (G∘G∘J)(y)= 因此 当x∈Θ时,G(x)=x,从而当y1=0时,G(J(y))=J(y),因此 -4G′((G∘J)(0,y2,…,yd))α(t,J(0,y2,…,yd),ν)= -4G′(J(0,y2,…,yd))α(t,J(0,y2,…,yd),ν). (13) 考虑(G∘G∘J)k(Y)的漂移系数 由于(G∘G∘J)′(0,y2,…,yd)=id,因此,此外,当(i,j)≠(1,1)时,是连续的.因此,由式(12)和(13)可得 G′(J(0,y2,…,yd))2α(t,J(0,y2,…,yd),ν)(ωωT)1,1(t,(0,y2,…,yd),ν)- 2G′(J(0,y2,…,yd))α(t,J(0,y2,…,yd),ν)(ωωT)1,1(t,(0,y2,…,yd),ν)=0, ∂xG(t,G-1(t,z,ν),ν)b(t,G-1(t,z,ν),ν). 由于z在dΘ上是内蕴Lipschitz连续的,因此,式(11)在dΘc也是内蕴Lipschitz连续的. 关于(t,ν)Lipschitz连续.从而,式(11)关于(t,z,ν)是Lipschitz连续函数. 下面证明映射 是Lipschitz连续的.由假设H2②、知y∂μG(t,G-1(t,z,ν),ν)(y)b(t,y,ν)在Θ上连续. 对μ,ν∈Pb,考虑μ(·)和ν(·)的耦合测度Π(·,·), b(t,x,μ)∂μG(t,G-1(t,z,ν),μ)(x)]Π(dy,dx)+ b(t,x,μ)∂μG(t,G-1(t,z,μ),μ)(x)]Π(dy,dx). p(G-1(t,z,μ))|Π(dy,dx)≤ CW2(μ,ν), (14) 是Lipschitz连续函数.类似地, |∂μα(t,p(G-1(t,z,ν)),ν)(y)- C|G-1(t,z,ν)-G-1(t,z′,ν)|≤C|z-z′|, |b(s,y,ν)||∂μα(t,p(G-1(t,z,ν)),ν)(y)- 是Lipschitz连续函数.由假设H1①、②知σ(t,z,ν)关于(t,z,ν)是Lipschitz连续且有界的,由假设H2②知∂y∂μG(t,G-1(t,z,ν),ν)(y)是Lipschitz连续且有界的,因此 是Lipschitz连续函数.证毕. □ 本小节考虑方程(1)的漂移系数可分解的情形,即对任意的x∈d,μ∈P2(d), b(t,x,μ)=b1(t,x)+b2(t,x,μ), 其中b1:[0,T]×d→d关于x为逐段Lipschitz连续函数, 对任意的t,t′∈[0,T],x,x′∈d,μ,μ′∈P2(d),存在常数L6>0使得 |b2(t,x,μ)-b2(t′,x′,μ′)|≤L6(|t-t′|+|x-x′|+W2(μ,μ′)). 由于 (15) 证明由引理4可知方程(5)的系数是Lipschitz连续的,Lipschitz连续可推出单调条件成立,因此,由文献[10]中theorem 2.1可知方程(5)有唯一强解Zt.当0 □ (16) 证明对任意的i=1,2,…,N, (17) □ 证明对给定的测度流(μt)t∈[0,T]∈C([0,T],P2(d)),由引理4知方程(5)有唯一强解.由引理4,BDG不等式,Hölder不等式和Gronwall不等式可得对(μt)t∈[0,T],(νt)t∈[0,T]∈Pb,∀t∈[0,T]有 (18) 对k≥0,t∈[0,T],定义Picard迭代 (19) (20) 由引理3及式(18)可得 (21) 选择常数C>0,0 □ 假设H3 假设H2②、成立,且 ① 假设H1①、H1②成立,对任意的t∈[0,T],x∈d,μ∈P2(d),存在常数L7>0使得‖σ(t,x,μ)‖≤L7. |b(t,x,μ)-b(t,x,ν)|≤6(t)W2(μ,ν). 另外,对任意的μ∈P2(d) ,xb(t,x,μ)在dΘ上满足逐段Lipschitz连续条件,且Lipschitz常数不依赖于分布. ③ 映射P2(d)μα(t,x,μ)是有界函数且属于且映射 P2(d)×d(μ,y)∂μα(t,x,μ)(y), P2(d)×d(μ,y)∂y∂μα(t,x,μ)(y), P2(d)×d×d(μ,y,y′) 有界且Lipschitz连续. (22) 当漂移系数不可分解时,由式(2)可得 此时 (23) 其中 0<ε0 GN(xN)=(G1(xN),…,GN(xN))T. 引理5 若假设H3③成立,0 证明由Hadamard逆函数定理(文献[16]中theorem 2.2)知要证GN可逆,只需要证GN满足:GN∈C1((d)N,(d)N×N),lim|xN|→∞|GN(xN)|=∞和对任意的xN∈(d)N,G′N(xN) 可逆.由GN的定义、α和的一致有界性,只需证明对任意的xN∈(d)N,G′N(xN) 可逆.注意到 从而G′N(xN)为线性算子id+A(xN):(d)N→(d)N.当0 □ (24) 其中 Bi(xN)=∂tG(t,xi,μxN)+∂xiG(t,xi,μxN)b(t,xi,μxN)+ (25) 引理6 若假设H3成立,则BN,ΣN满足局部Lipschitz连续性和线性增长条件. 证明由∂xG(t,x,μ)和∂μG(t,x,μ)(y)关于(x,μ)Lipschitz连续及式(25)可得对xN,yN∈(d)N, ‖ΣN(xN)-ΣN(yN)‖2≤ C|xN-yN|2, 其中,最后一个不等式用到了假设H1②、假设H3①和引理1. |Bi(xN)-Bi(yN)|2≤ C|∂xiG(t,xi,μxN)b(t,xi,μxN)-∂yiG(t,yi,μyN)b(t,yi,μyN)+ tr[σT(t,yk,μyN)∂y∂μG(t,yi,μyN)(yk)σ(t,yk,μyN)]|2+ 由假设H3①和H3③可得Π3,Π4和Π5是有界且Lipschitz连续的. LR|xi-yi|2. 从而 由文献[2]中lemma 3.6、lemma 3.9和lemma 3.11可得 是Lipschitz连续函数.由假设H3①—H3③可得 最后,由b,σ满足增长条件和G,α导函数的有界性可得BN,ΣN满足线性增长条件,即存在常数C>0,使得对任意的xN∈(d)N,|BN(xN)|+‖ΣN(xN)‖≤C(1+|xN|).证毕. □ 本文在系数关于空间变量不是Lipschitz连续的条件下,借助于Zvonkin变换得到了一类分布依赖的高维随机微分方程及相应的粒子系统解的存在唯一性.本文中Zvonkin变换的变换函数不同于文献[1]中系数不依赖于时间和分布的一维随机微分方程情形下的变换函数.本文的变换函数不仅和状态有关,还和时间以及分布有关.为了得到变换后的方程解的存在唯一性,本文重点考虑了分布函数关于每个分量的Lipschitz连续性,进而通过逆变换得到了原方程解的存在唯一性.本文的结论有效地补充了文献[1-2,7].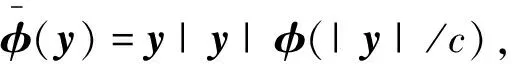

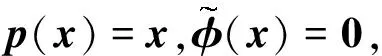
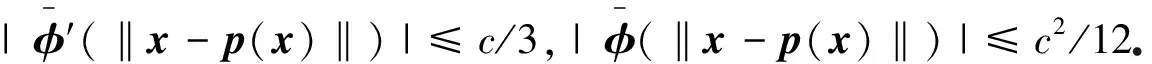
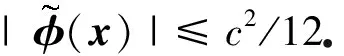
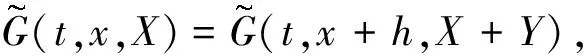
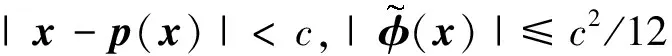

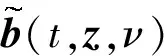
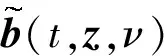
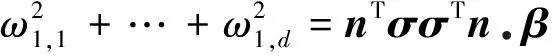
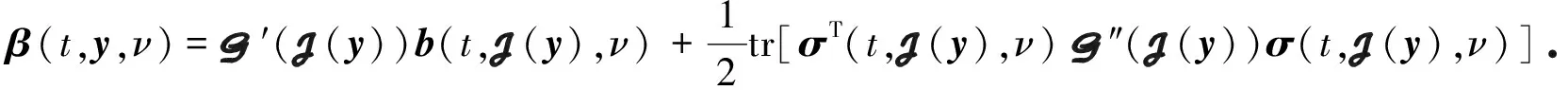
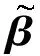
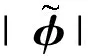
2 主 要 结 果
2.1 漂移系数可分解的分布依赖随机微分方程及交互作用粒子系统
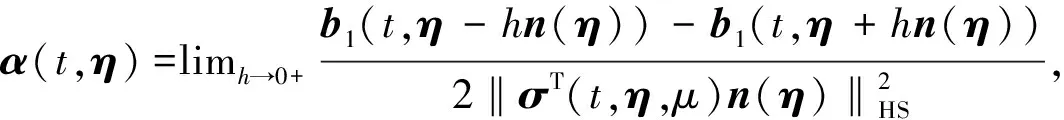
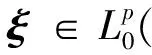

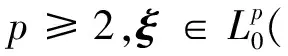
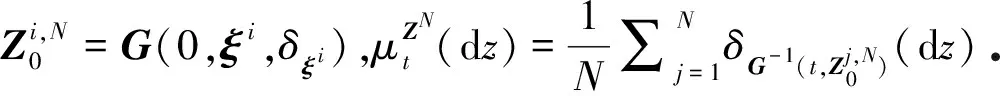

2.2 漂移系数不可分解的分布依赖随机微分方程及交互作用粒子系统
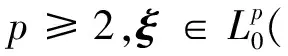

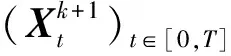

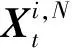


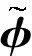

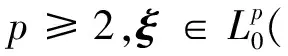

3 结 论
