基于遗传算法的公路自动选线与安全评价方法

朱雷鹏, 张贵阳, 张志清*

(1.北京工业大学城市交通学院交通工程北京市重点实验室, 北京 100124; 2.中国电建市政建设集团有限公司, 天津 300384)

目前,中国公路选线设计体系依赖于专家经验知识,基于公路选线设计规范标准,通过试凑法,从备选方案中比选出一条符合标准的线路[1-2]。但公路选线需要统筹考虑大量的影响因素,是一项复杂的系统工程,而传统人工选线方法设计的备选方案有限,选线设计人员的经验程度不同,很难找出全局最优或者接近最优的公路路线设计方案,并且容易漏掉优秀的选线方案,这在一定程度上降低了选线的效率与质量[3-4]。因此,提出一种能够实现公路自动选线的智能化方法,是道路勘测设计领域亟须解决的科学问题之一。

自动选线可提升选线方案的质量与综合决策效率,是一种新型高效的线形设计方法[5]。随着计算机技术的发展,国内外学者提出了大量自动选线寻优方法。主要有距离变换法、网络自适应直接搜索、遗传算法等。其中,距离变换法和网络自适应直接搜索可结合选线经验,在地形简单的平原、丘陵地区实现自动选线,但在复杂地形环境下难以得到可行的选线结果[6]。而遗传算法具有高效的全局搜索能力与求解速度,可处理复杂的非线性约束,已在自动选线研究中得到了广泛应用[7-8]。其中,You等[9]基于遗传算法,构建了以线路设计规范为约束,以经济性、安全性为目标函数的线形优化模型,选线结果有利于提高公路安全性,减少选线工作人员的冗余调试工作。李成谦等[10]通过识别诸多线形设计参数中的风险因素,构建了基于成本-安全均衡的自动选线模型,通过遗传算法求解表明,该模型显著提高了公路的安全性与成本效益,并在川藏高速公路工程中得到了应用与验证。张驰等[11]基于遗传算法,结合Rhino+Grasshopper平台,构建了考虑风景环境的自动选线模型,缓解了既有自动选线方法在小区域范围内选线结果不准确的难题。刘光伟等[12]引入分阶段的选线剖面布置形式,结合线路几何特性与工程费用,构建了露天煤矿自动选线模型,利用遗传算法求解表明,相比于手工定线方法,优化后的模型能够快速、高效地找出费用最低的选线方案。同时,部分学者还构建了基于生态视角的公路自动选线模型,进一步丰富了公路自动选线的研究体系[13]。此外,为了探究更合理的路线评价方法,有学者认为有必要对公路平纵组合的安全性进行评价,进一步提升公路的选线效率与安全评价水平[14]。

综上所述,既有基于遗传算法的公路自动选线研究成果,主要集中在构建公路线形的表示方法和建立目标函数两个方面,仍然存在不足。一是大部分研究将平面交点的选择方式假定为等距分布,并在规定剖面上搜索其合理位置,而在实际选线过程中,公路平面交点位置应在选线区域内进行随机搜索,该假设与实际情况并不相符;二是既有研究对选线方案的安全性评价仍待进一步完善。因此,现拟在重点考虑自动选线方案安全性的基础上,建立基于遗传算法的自动选线优化模型,在选线区域内随机搜索平面交点位置,力争实现拟定选线区域路线方案的自动寻优。

1 自动选线流程设计与路线表达

1.1 选线流程设计

遗传算法是求解复杂优化问题全局最优解的有效算法[15-16]。基于遗传算法的公路自动选线与安全评价方法流程如图1所示。

图1 基于遗传算法的公路自动选线与安全评价方法Fig.1 Highway automatic alignment selection and safety evaluation method based on genetic algorithm

1.2 公路路线表示

公路路线模型由平面和纵断面线形组合而成,如图2和图3所示,假设S(XS,YS)、E(XE,YE)为路线的起终点,在起点S和终点E之间选择n个不同的点作为路线交点,确定合适的平曲线半径。为了便于研究,按《公路路线设计规范》(JTG D20—2017)(以下简称规范)选取固定长度的缓和曲线。公路线形优化就是不断搜索优化路线交点位置、圆曲线半径、竖曲线半径及变坡点高程的过程。

图2 公路平面线形示意图Fig.2 Schematic diagram of highway plane alignment

图3 公路纵断面线形示意图Fig.3 Highway longitudinal section alignment schematic

2 公路线形约束模型

基于《公路路线设计规范》(JTG D20—2017),考虑公路平面、纵断面以及平纵组合等关键线形技术参数,构建公路线形约束模型。

2.1 公路路线平面约束

路线平面约束主要包括路线的圆曲线半径(R)、平曲线间夹直线长度(L)、直线长度(LZ)、平曲线长度(LC)等方面的约束。

(1)

式(1)中,rj、lj、lzj、lcj分别为路段j圆曲线半径、平曲线间夹直线长度、直线段长度以及平曲线长度的取值;rmin、lmin、lzj、lcmin分别为规范里对平面应线形参数的最小值。此外,平曲线间夹直线长度(lzj)在满足规范的基础上,为提高公路平面线形的平顺性,还应符合式(2)的规定。

式(2)中:v为路段j的设计速度。

2.2 公路路线纵断面约束

路线纵断面约束主要包括路线的纵坡(I)及坡长(LD)等方面的约束。

(3)

式(3)中:ij、ldj路段j坡度与坡长的取值;imin、ldmin分别依据设计速度从《公路路线设计规范》(JTG D20—2017)中进行取值,其中,imin≥0.3%。

2.3 公路路线平纵线形组合约束

为保证线形设计一致性及行车安全,公路自动选线要求竖曲线起点与终点在平曲线内。

3 路线基因编码与初始方案生成

3.1 路线基因编码

连续搜索选线区域,高效确定公路交点线形技术参数是实现公路自动选线的关键技术问题。在实数编码中,不仅可以简化编码过程,还能够保证路线方案的全局最优性能,因此选择实数编码对公路三维空间基因编码进行改进。公路自动选线基因编码过程如图4所示。

图4 公路自动选线基因编码过程示意图Fig.4 Schematic diagram of the genetic coding process for automatic highway routing

实数编码时,公路路线的基因编码可以归结为:平面交点坐标(X,Y)、圆曲线半径(R)、变坡点高程(hz)、竖曲线半径(hr)。则公路个体基因型为X、Y、R、hz、hr。其中X、Y、R、hz、hr均为n维向量,表示平面n个交点。

3.2 路线初始方案生成

根据公路路线方案的基因编码,可以生成路线方案初始种群。首先随机产生n个交点,然后再按照起点到终点之间的顺序,在这n个点处布设直线、圆曲线和缓和曲线,最后加上竖曲线,组成一个初始路线方案。重复产生m个初始路线,便形成了包含m个体的初始方案种群。

4 路线适应度函数与遗传算法

4.1 适应度函数

4.1.1 目标函数

选择公路修建总费用(C)作为目标函数。公路修建总费用的计算公式为

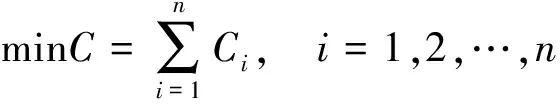
(4)

式(4)中:n为公路修建过程中费用的类别数;Ci为第i类具体费用(例如,拆迁补偿、工程建设以及设备租赁等费用)。

4.1.2 适应度值

公路自动选线的目标是通过不断计算目标函数,同步调整具体设计方案,以适应度值作为择优标准,对设计方案进行比选,从而在众多方案中得到最优方案,实现公路选线的自动优化决策。适应度函数的计算公式为

fi=Cmax-Ci

(5)

式(5)中:fi为第i代选线方案的适应度值;Cmax=max(Ci)为各类费用的最大值。

4.2 遗传算法实现自动寻优

为了使路线能够避开不利地形,实现智能设计调整路线位置与平纵线形关键技术参数,基于遗传算法通过设计选择算子、交叉算子及变异算子实现公路路线及线形关键技术参数的不断寻优。为了保证选线方案的不断优化和保留每一代优化方案,在遗传算法模型中采用最佳个体保留法,将每一代中适应度最高的5个选线方案作为基础方案参与子代的迭代过程。

5 公路安全性评价

平纵线形满足技术规范标准的路线也不一定满足舒适、安全的行车需要,因此有必要检验其安全性能[17]。利用遗传算法得到的平纵线形技术参数,预测各路段运行速度,以相邻路段之间运行速度的差值作为公路线形设计与运营一致性的评价指标,评价选线方案中关键线形参数的合理性。

5.1 寻优路段分类

根据公路线形的不同平纵组合,将整条公路划分为4种形式,路段划分标准如表1所示。

表1 路段划分标准

5.2 运行速度测算

选取二级公路为研究对象,确定车辆类型为小汽车,基于遗传算法每一代产生的选线方案中平纵线形技术参数,对各路段运行速度进行预测。

5.2.1 平直路段

在平直路段,视距和线形条件通常较好,驾驶人员为获得更好的驾驶体验,往往想达到期望速度,当行驶速度低(高)于期望速度时,会发生加(减)速行为。直线路段出口处的运行速度按式(6)测算。

ifv0=vpre

thenvout=v0;

else ifv0≠vpre

(6)

式(6)中:v0、vout、vpre分别为直线路段入口处的入口速度、出口速度及运行速度,其中v0取80 km/h;a0为汽车的加速度,当a0>0时,a0∈[0.15,0.5]m/s2;当a0<0时,a0∈[-0.5,-0.15]m/s2;S为直线路段的长度,km。

5.2.2 纵坡路段

纵坡路段的运行速度主要受坡度与坡长的制约,可忽略由平面线形带来的影响,因此以坡度和坡长为约束条件对纵坡路段的入口速度进行修正。纵坡段运行速度修正标准如表2所示。

表2 纵坡段运行速度修正标准

5.2.3 小半径平曲线路段

小半径平曲线段的运行速度按式(7)测算[18]。

vout=12.26+0.83v0+5.73R

(7)

式(7)中:R为平曲线半径,km。

5.2.4 弯坡组合路段

弯坡组合路段的运行速度按式(8)测算[18]。

vout=-4.38+0.55v0+0.72vmiddle+11.71lnR+0.18Inow1-1.44Inow2

(8)

式(8)中:vmiddle为车辆在平曲中点处的运行速度,km/h;Inow1、Inow2分别为平曲线段前(后)直线坡度,%。

5.3 评价指标

相邻路段运行速度的差值(Δv85)是衡量道路线形设计安全性的重要指标[19]。基于Δv85设计道路线形一致性评价流程,如图5所示。

图5 基于Δv85的道路线形安全性评价流程Fig.5 Road alignment safety evaluation process based on Δv85

6 选线实例

6.1 选线区域介绍及算例参数取值

6.1.1 选线区域介绍

为了验证算法的可行性,以北京市黄松峪地区为自动选线试验区域,以实现公路路线的自动搜索和优化。黄松峪地处北京市平谷区,地势北高南低,海拔在100～120 m,所选区域选线区域起讫点坐标分别为:S(477 772.98, 320 625.08)、E(478 204.23, 321 791.85)。

6.1.2 算例参数取值

进行算例参数取值前,已对研究区域的地形、地质、人文及水文等影响公路路线走向的因素进行了前期调查,并对数据进行了转换处理。参考《公路路线设计规范》(JTG D20—2017),对公路线平面、纵断面及横断面关键技术参数进行了取值,公路路线基本参数如表3所示。同时对遗传算法基本参数进行取值,遗传算法基本参数如表4所示。

表3 公路路线线形基本参数

表4 算法基本参数

为实现自动选线,在选线区域产生2个平面交点以生成公路选线初始方案群,公路初始种群适应度值示例如表5所示。

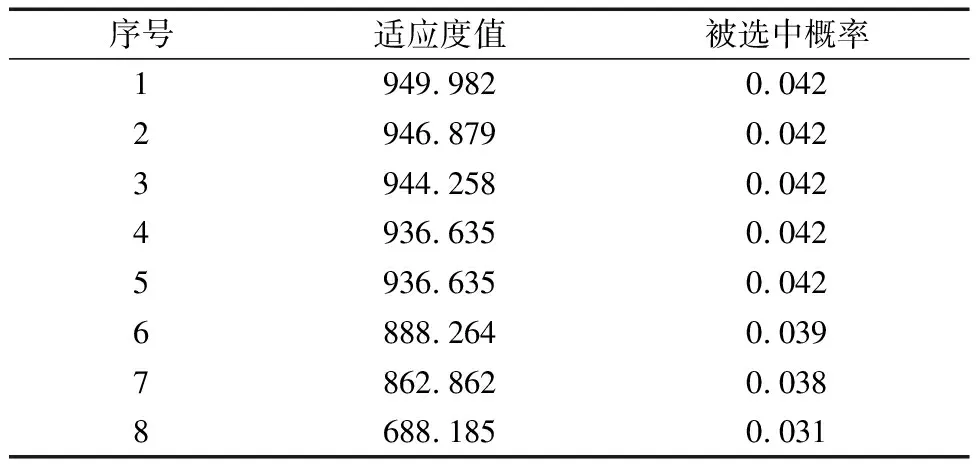
表5 公路初始种群适应度值示例

6.2 选线结果分析

结合公路线形平面、纵断面、平纵组合技术指标约束条件,设计遗传算法,在对每代选线方案进行安全性评价的基础上,输出每一代公路自动选线的路线长度、总费用的最优结果,每一代路线基本信息如表6所示。每一代最优路线总费用、每一代最优路线长度分别如图6、图7所示。

表6 每一代路线基本信息表

图6 每一代最优路线总费用迭代图Fig.6 Iteration chart of total cost of optimal alignment of each generation

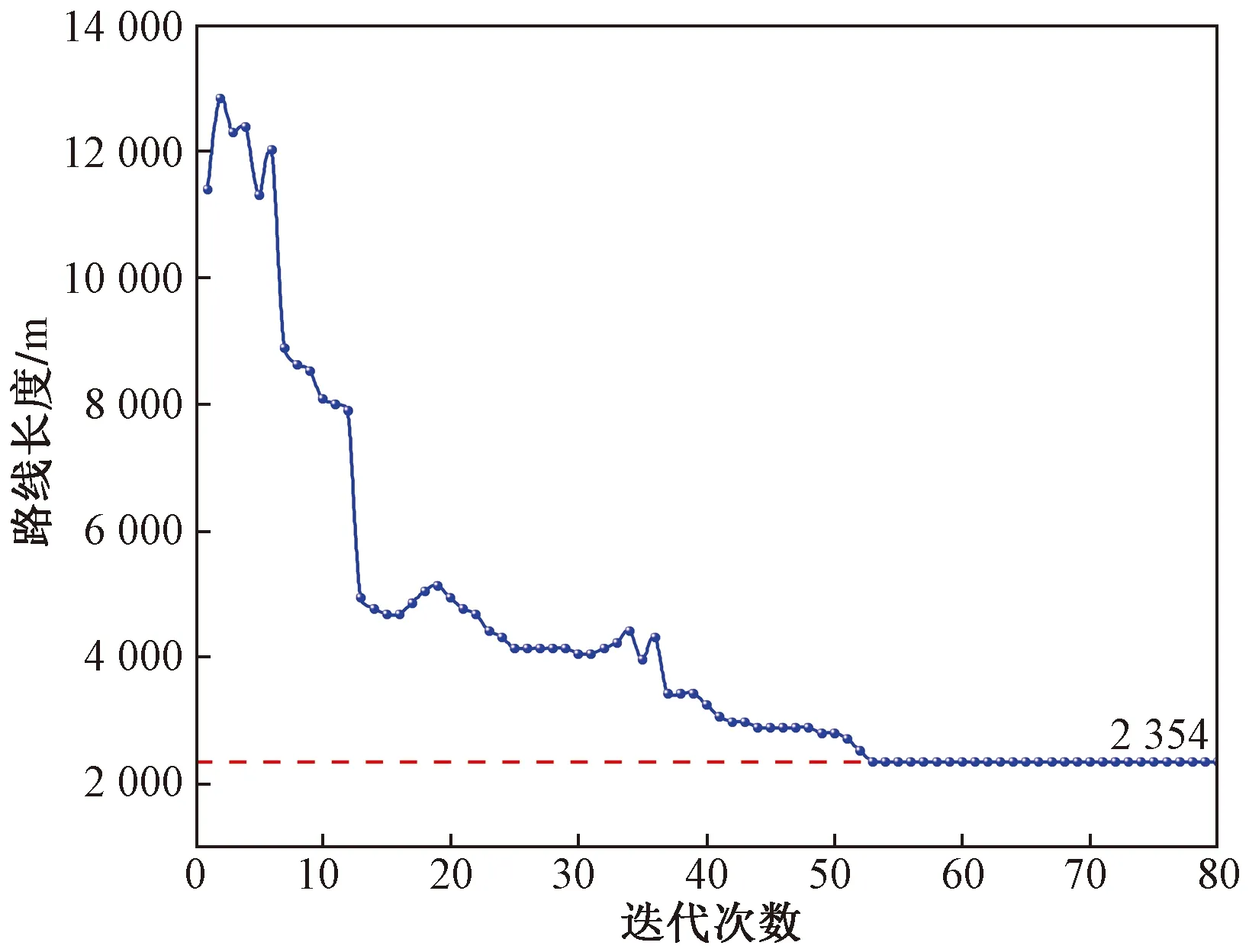
图7 每一代最优路线长度变化图Fig.7 Iteration chart of total cost of each generation of optimal alignment and change chart of length of each generation of optimal alignment

由表6可得,相邻路段的速度差均小于 20 km/h,符合公路选线线形安全性标准,表明所引入的运行速度预测模型,可以满足公路选线方案的安全性审查要求。同时,最大纵坡、最小半径、最小坡长均满

足公路线形约束条件,表明基于遗传算法设计的公路自动选线与安全评价方法能够满足公路选线基本规范的要求,可作为公路自动选线的优化方法。

由图6和图7可知,公路路线的工程总费用变化趋势与路线长度变化基本相似,工程总费用的变化更能体现公路自动选线优化的特点,迭代初始迅速优化,迭代中期优化速度放慢,接着优化速度趋于平缓,最后保持不变。说明随着迭代次数的不断增加,选线方案在公路路线平面、纵断面、平纵组合的约束条件下逐渐趋于最优,与现实情况相符,表明本文构建的模型,能够在保证公路线形安全的基础上,得到全域最优的选线方案。迭代至第53代,在满足平面线形技术标准要求及安全性标准的条件下,选线方案达到最优,并得到关键线形技术参数。其中,线路长度为2 354.71 m、最大坡度为3.5%、最小曲线半径为500 m、最小坡长为193.94 m、相邻路段速度差为13.1 m/s、总费用为549.68 万元,选线方案达到了最优。

综上,基于遗传算法的公路自动选线模型,在考虑路线安全性条件下,可以同时保证路线交点在拟定的选线区域全局进行自动搜索,验证了公路自动选线方法的可行性,可以实现公路路线的自动选择和优化,能够显著提高公路选线的工作效率。

7 结论

针对现有公路选线模型在平面交点确定方法与安全性评价等方面问题,基于遗传算法,建立了路线优化模型,并设计了公路安全性评价方案,基本实现了公路选线方案的自动寻优和主动安全评价。

(1)基于遗传算法,分别从公路平面、纵断面以及平纵组合3个方面构建了公路路线约束模型,从安全性和经济性层面选取指标作为选线方案评价标准,建立了公路自动选线优化模型。

(2)通过在选线区域内随机设置公路路线的平面交点,实现了选线全域范围内所有选线方案的自动优劣比较,保证了所选公路路线方案的全局域最优,提升了选线方案的决策效率,弥补了传统选线方法的不足。

(3)将相邻路段的运行速度差作为评价线形安全的理念引入现代公路设计体系,构建了运行速度预测模型,与传统直接依据公路设计标准规范设计的选线方案相比,可提升公路选线方案的安全等级与经济效益。