移动荷载作用下Gibson地基中Duxseal主动隔振研究
赵礼治,高 盟,张致松
(1. 山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛 266590; 2. 山东科技大学 土木工程与建筑学院,山东 青岛 266590)
0 引言
工程中的振动多通过地基传播,为有效减轻列车运行对沿线建筑的振动影响,通常在列车沿线设置屏障隔振。目前,国内外已取得很多研究成果和进展。KAYNIA等[1]采用Kausel-Ro⊇sset-Green函数计算地基-路堤界面处的土壤刚度矩阵,计算了埋置道碴或道下埋置刚性板(即波阻板)的隔振效果。TAKEMIYA等[2]将列车简化为n个轮对组成的车,采用离散波数法和快速傅立叶算法对该空间-时域进行逆变换,得到列车移动荷载的形式。YANG等[3]采用有限元/无限元方法,分析不同的波浪屏障对列车通过时引起的地面振动的减振效果,得出不同屏障最佳参数值的选择方法。AUERSCH[4]创建了一个综合模型,同时计算车辆-轨道相互作用以及列车经过出现的地面振动。巴振宁等[5]基于2.5维间接边界元法(indirect boundany element method, IBEM)研究了轨道列车在层状地基中空沟的隔振效果,分析讨论了屏障及地基参数对隔振效果的影响。基于饱和土Biot理论,徐斌等[6]利用2.5维边界元法(boundary element method, BEM)得出移动荷载下空沟对饱和土的动力响应。傅玉勇[7]通过数值模拟的方法研究高速铁路隔振沟的隔振效果,分析得出随着深度的增加,土颗粒间动力响应明显降低。蔡袁强等[8]基于2.5维有限元法(finite element method, FEM),研究地铁列车运行时填充沟对地基振动的隔振效果,分析隧道埋深及填充沟尺寸对隔振效果的影响。谢伟平等[9]建立列车-隧道-地基计算模型,使用数值模拟软件分析波阻板(wave impedance block, WIB)对地铁振动的隔振效果,得出WIB对地铁的低频振动特别是10 Hz以内的振动隔振效果明显。CHOUW等[10]提出在地基中设置波阻板实现隔振目的,并利用二维边界元法证明其隔振效果较空沟表现更优异。高广运等[11]利用薄层法推导出三维饱和地基基本解,研究WIB主动隔振,得到轨道交通荷载下WIB在饱和地基中的主动隔振规律。孙雨明等[12]采用薄层法讨论Gibson地基中WIB的隔振效果,分析得到不同参数对隔振效果的影响。TAKEMIYA[13]提出了蜂窝状波阻板(honeycomb wave impedance block, HWIB)这一新型隔振措施,基于现场试验分析HWIB的隔振效果。高盟等[14]提出一种将Duxseal填充至带孔波阻板的联合隔振方法(Duxseal-WIB, DXWIB),通过现场试验,得到不同参数下DXWIB屏障的隔振效率。
然而,空沟具有良好的隔振性能,但开挖深度较浅且受限于土体自身稳定性,导致其实际应用受到较大限制[15];填充沟通过填充材料弥补空沟隔振的不足,但隔振效果仅在沟后一定区域较好[16];传统的波阻板屏障隔振频率窄,隔振效率低,已经不能满足日益严格的隔振需求[9]。基于此,提出Duxseal材料的新型主动隔振方法,以此减少环境振动污染。
基于井上滕夫等[17]提出的方法建立了列车-轨道振力模型,选取文献[18]中的移动荷载为激励。随后,建立一种适合于求解土体介质中动力相互作用问题的半解析边界元法计算模型,详细研究轨道交通荷载作用下三维均质半空间和Gibson地基中Duxseal的隔振效果,提出了Duxseal隔振体系设计的基本准则,为Duxseal用于轨道交通隔振的工程实践提供理论基础。
1 三维边界元方程推导
1.1 列车激振荷载的计算
考虑列车-轨道的动力相互作用,将列车荷载模型简化为列车-轨道简化分析模型。列车荷载模型如图1所示。
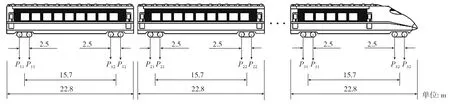
图1 列车荷载模型[17]
列车-轨道简化分析模型中,轨下基础沿纵向被离散。离散以各轨枕支点为基元,每个支承单元采用双质量(轨枕和道床)3层(钢轨-轨枕-道床-路基)弹簧-阻尼振动模型。列车-轨道分析模型如图2所示。
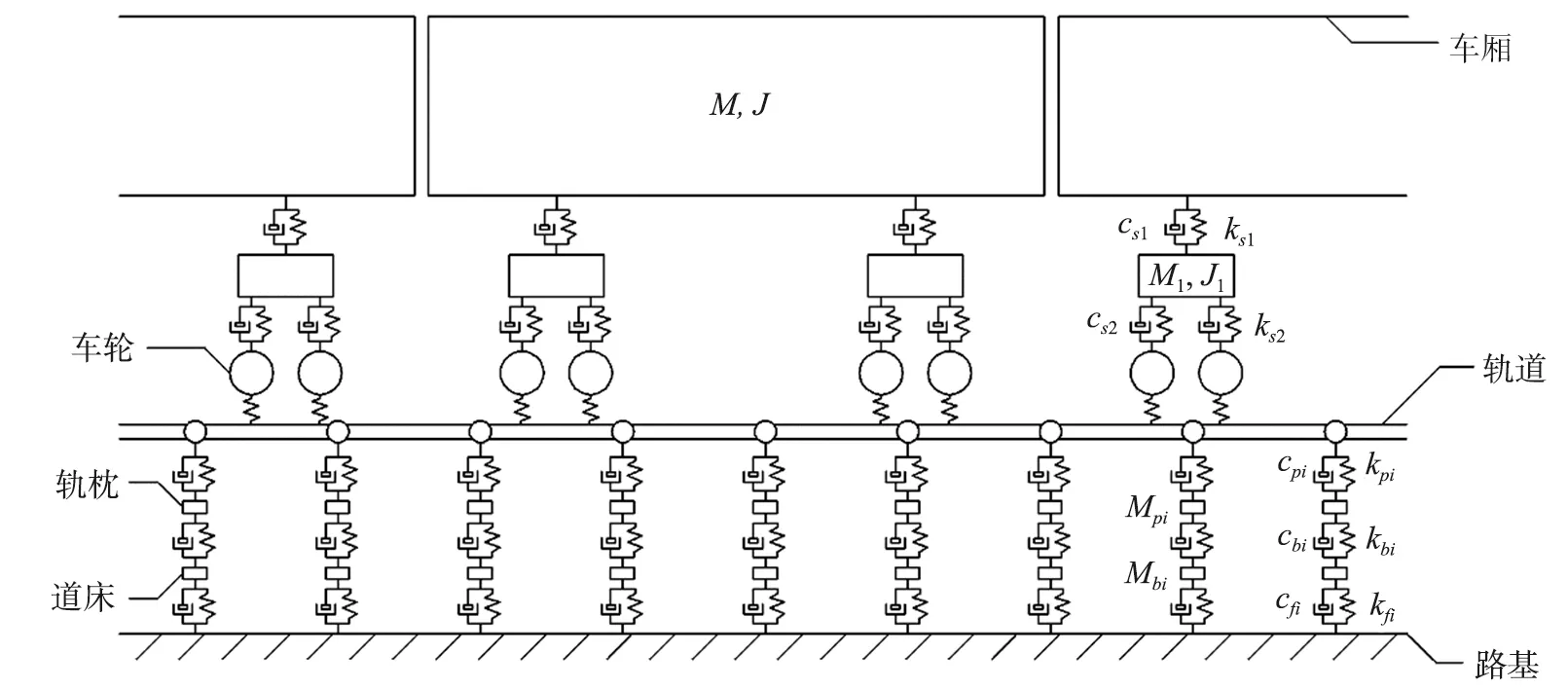
注:M为车体质量(kg); J为车体转动惯量(kg·m2); M1为转向架簧上质量(kg); J1为转向架转动惯量(kg·m2);
计算参数如表1所示,其中每节车厢有2个轮对。钢轨单轮通过轨道时,竖向准静荷载持续时间T0= 0.132 s,频率f1为3.788 Hz,荷载峰值P1m=44.5 kN。车-轨体系对轨道产生的动荷载峰值P2m=11.0 kN,单个轮重m=1404 kg,轨道截面抗弯刚度EI=6.627×106N/m2,设支承跨度为l=1.1 m,共振频率f2=65.55 Hz。
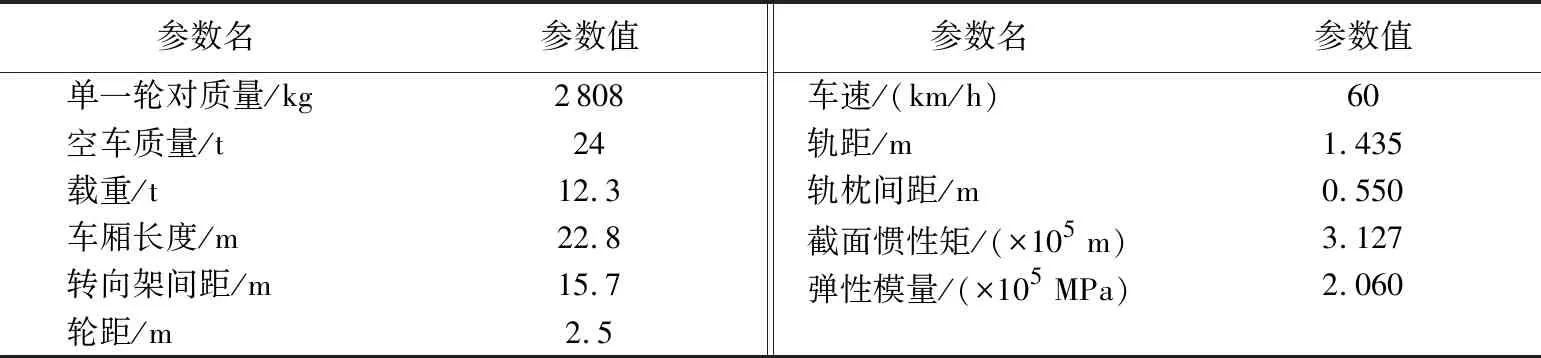
表1 列车计算参数
根据文献[18],可以得到单轮通过轨道时的激振力时程为:
P1(t)=44.5 sin(2π×3.788t)+11.0 sin(2π×65.66t) 0 s≤t≤0.132 s
(1)
将式(1)代入式(2)中,则可以叠加计算车轮数量为n的列车同时通过轨道时对道床的激振荷载:
(2)
式中:xi为第1个轮与第i个轮的距离;v为车速。
1.2 三维地基薄层法的基本解答

(3)
式中:λ、G为拉梅常数;r,θ和z分别为柱坐标系下轴向、切向和竖向坐标;u,v和w分别为柱坐标系下轴向、切向和竖向位移;Θ为体变。
薄层法的基本微分方程,即位移u1,u2,u3关于深度z的常微分方程:
(4)
式中:ρ为介质密度;k为波数;ω为圆频率。
对各层进行集总后可得薄层法的基本方程:
(5)
1.3 三维半解析边界元法
根据Betti-Rayleigh互等定理及Somigliana恒等式,不考虑体力,可得到频域内弹性体边界积分方程:
(6)

对于具有N个边界节点的问题,与N个边界节点处的面力、位移相关的线性方程组可以表示为:
(7)

2 边界元法验证
根据推导的薄层法基本解,编写了三维半解析边界元计算程序,与王贻荪[19]和AHMAD等[20]的计算结果进行对比。
1)选取文献[19]的计算参数,取土体的密度ρ=1800 kg/m3;剪切模量μs=53 MPa;泊松比vs=0.25;激振频率f=16 Hz,本文的算法与王贻荪的Lamb问题解答对比如图3(a)所示。振动过程自加荷后开始考虑,Lamb问题的求解可通过突加力问题的闭合解求得,可有效避免求积难以计算的积分形式解。由图3(a)可知,本文的计算结果与文献[19]的结果基本一致。
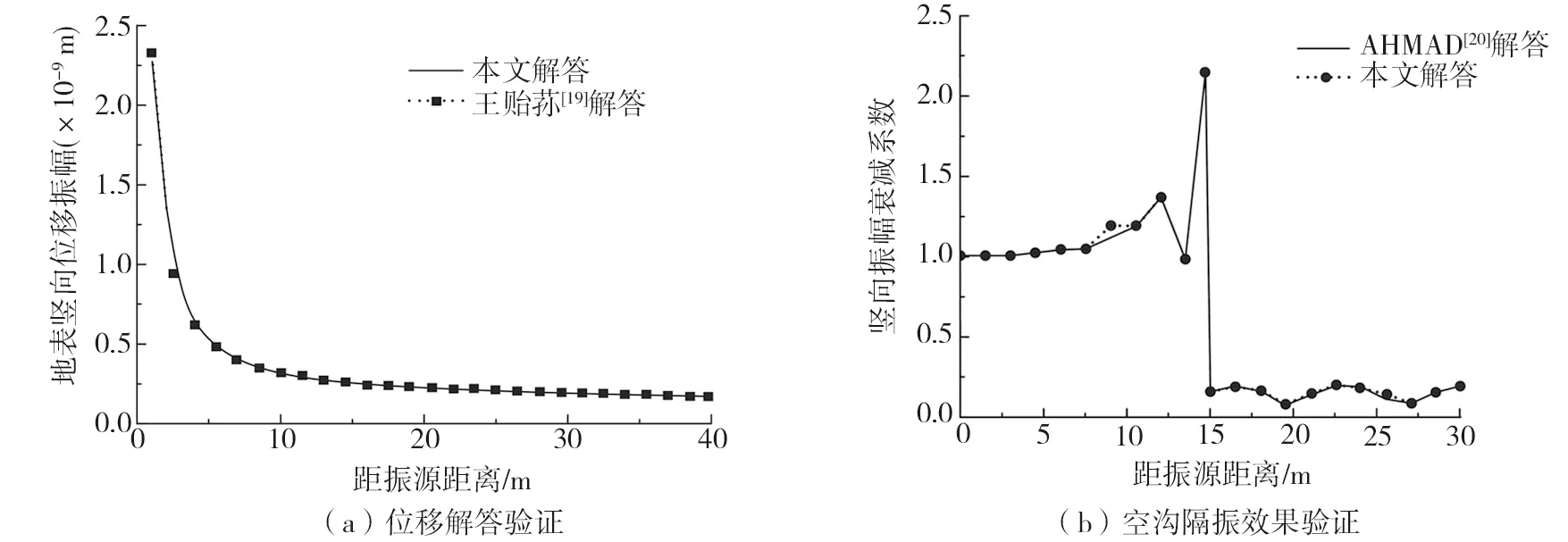
图3 薄层法和边界元法模型验证
2)选取文献[20]的计算参数,取土体密度ρ=1800 kg /m3;剪切模量μs=46 MPa;泊松比vs=0.25;空沟深度h=1.0λR(λR为Rayleigh波长);沟宽w=0.1λR;距振源距离d=5λR;基础宽度t=0.25λR;竖向简谐激振频率50 Hz。由图3(b)看出两者计算结果几乎相等。通过与文献[19]和文献[20]的比较说明本文计算模型的可靠性。
3 Duxseal主动隔振分析
将地基中某一薄层设置为Duxseal,如图4所示。根据推导的薄层法边界元基本解,编写MATLAB程序,计算列车移动荷载作用下Duxseal的隔振效果。定义振幅衰减系数AR[21],分析埋深、宽度、厚度对Duxseal主动隔振性能的影响。
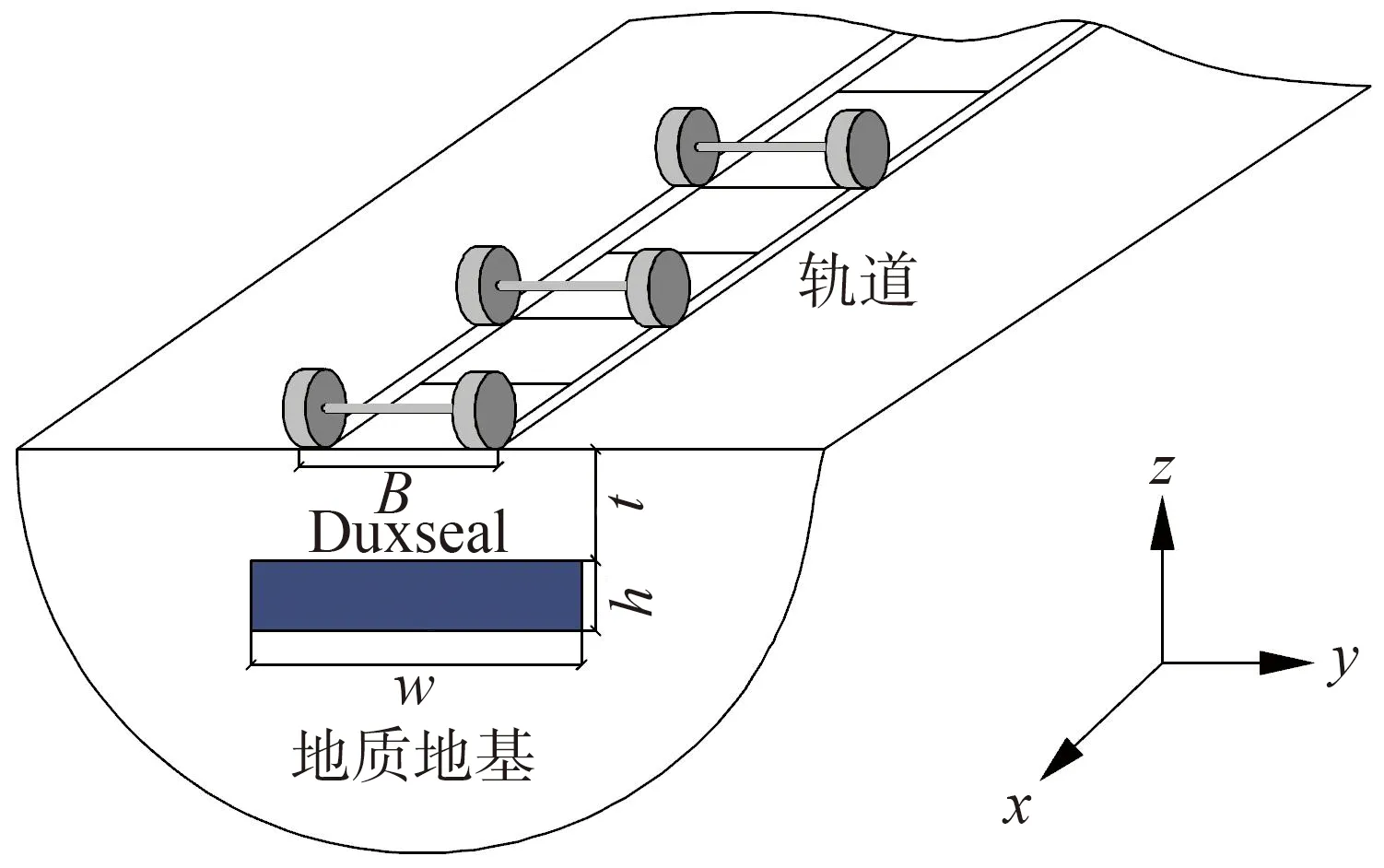
图4 Duxseal主动隔振示意图
(8)
作用在轨道上的激振荷载用式(1)代入,轨道宽度B取为1.5 m。模型长度x方向取列车的长度为136.8 m,如图1所示,宽度y方向取无限长,深度z方向底部边界为旁轴边界。轨道下设置与列车长度相同的Duxseal隔振体系,其宽度、厚度和顶板埋深分别为w、h和t,计算时,采用轨道宽度B对相关几何尺寸进行归一化。
3.1 均质地基Duxseal主动隔振
土体及Duxseal的计算参数如表2所示。取地基的黏滞阻尼比为ξs=0.05,土体中R波的波速为160 m/s。

表2 土体和Duxseal计算参数
1)厚度
为了探究不同Duxseal厚度对隔振效果的影响,选取Duxseal的宽度w=6B、埋深t=0.667B,设置Duxseal厚度h分别为0.333B、0.667B、1.333B、2.667B、5.333B。水平向和竖向AR随振源距的关系曲线如图5所示。
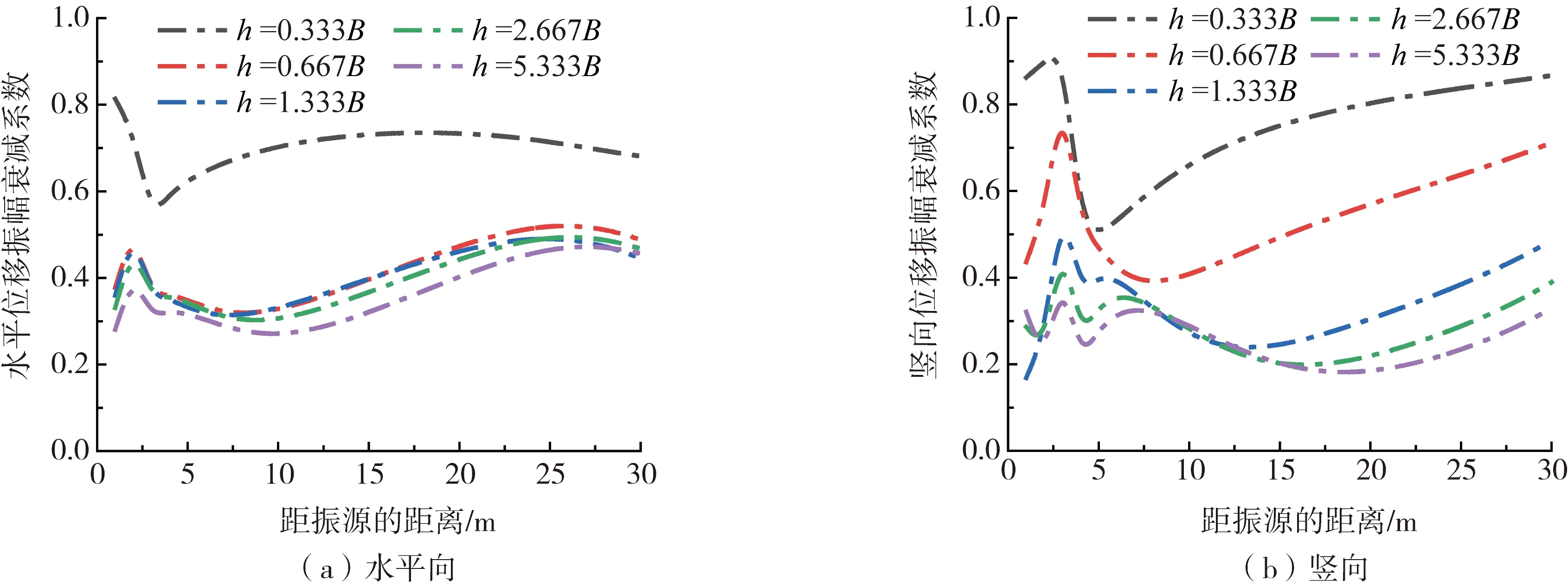
图5 均质地基中Duxseal隔振效果随厚度的变化
由图5可知,移动荷载作用下,与其他厚度的Duxseal材料相比,当Duxseal的厚度较小时(h=0.333B),Duxseal的隔振效果较差;随着厚度的增加,隔振效果显著提升。近场水平位移振幅衰减系数变化趋势不一致,说明厚度变化对于近场隔振较为敏感,这表明近场隔振存在一个较优厚度。随着振源距的增大,变化趋势逐渐趋于一致。当厚度增加到一定数值(水平方向h=0.667B,竖向h=1.333B),此时厚度增加,隔振效果变化幅度较小且趋于稳定。从隔振距离观察,Duxseal在近场的隔振效果较好,随着距离的增加,隔振效果逐渐变差。随着距离的增加,竖向隔振产生较大波动。水平方向距离l为5~10 m和竖直方向距离l为0~5 m的隔振效果好。因此,考虑到成本问题和隔振效果,厚度取h=1.333B较为合理。
2)宽度
为了探究不同Duxseal宽度对隔振效果的影响,选取Duxseal的厚度h=0.667B、埋深t=0.667B,设置Duxseal宽度w分别为2B、4B、6B、8B、10B。水平向和竖向AR随振源距的关系曲线如图6所示。
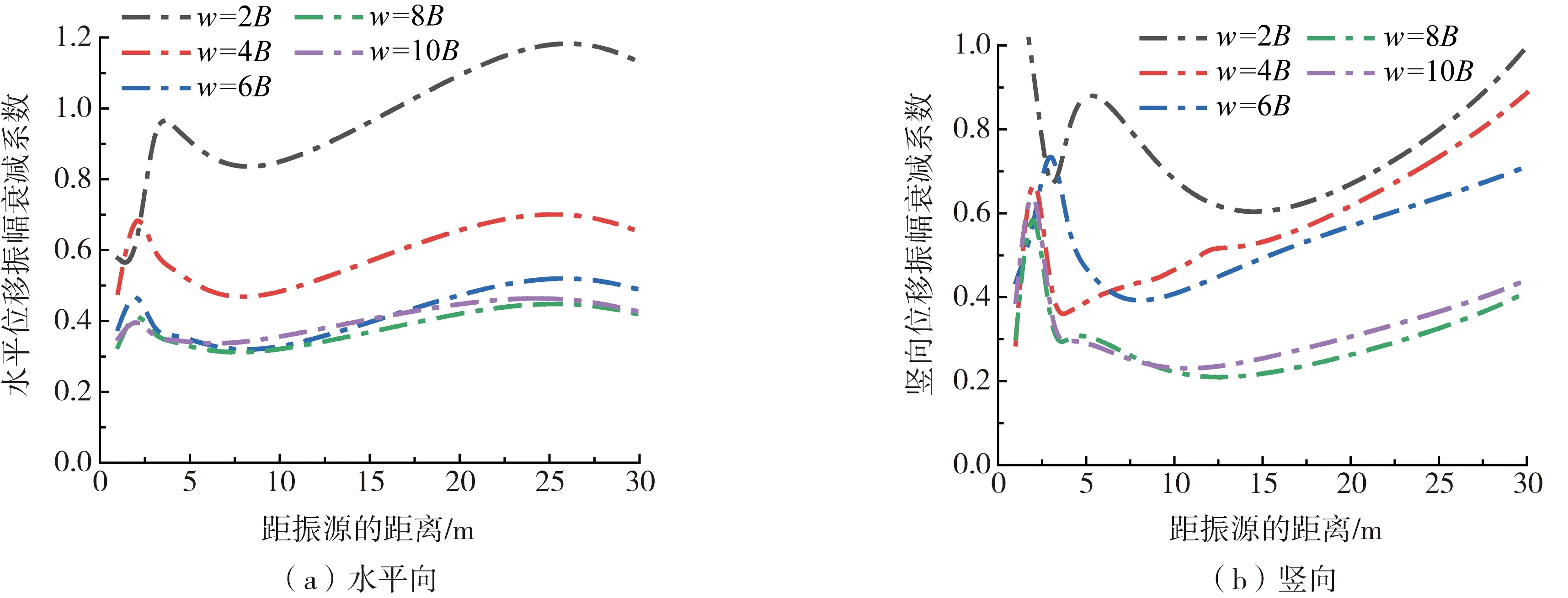
图6 均质地基中Duxseal隔振效果随宽度的变化
由图6可知,移动荷载作用下,水平方向的隔振效果随着Duxseal宽度的增加而增大。水平向和竖向上宽度分别大于6B和8B时,Duxseal宽度的增加对隔振效率的提升较小且趋于稳定。因此,在一定范围内提高Duxseal宽度能有效增强隔振效果。从隔振距离来看,水平和竖直方向在距振源5~10 m隔振效果均达到最优;但在远场(l>20 m),水平方向上AR> 1,此时出现振动放大现象。因此,为充分发挥材料隔振性能,Duxseal宽度应选取w=8B。
3)埋深
为了探究不同Duxseal埋深对隔振效果的影响,选取Duxseal的厚度h=0.667B、宽度w=6B,埋深t分别为0、0.333B、0.667B、1.333B、2.667B。水平向和竖向AR随振源距的关系曲线如图7所示。
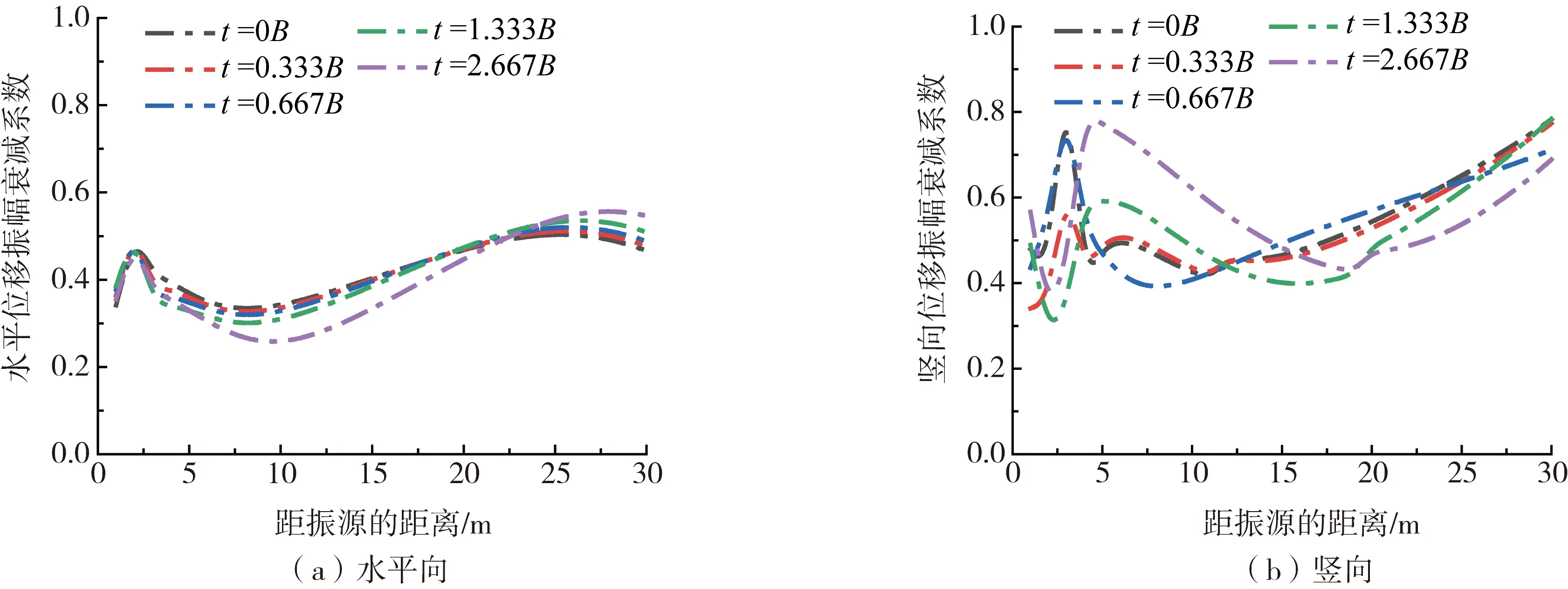
图7 均质地基中Duxseal隔振效果随埋深的变化
由图7可知,水平向隔振受到埋深的影响较小;但竖向隔振随埋深的变化产生较大波动。较小的埋深下,水平和竖向的隔振效果较好,且施工难度小。从距离来看,当距振源距离l<15 m及l>15 m时,竖向最大隔振效果分别可达到70%和60%,此时的埋深均为t=1.333B。因此,综合考虑成本及隔振效率,埋深选择t=1.333B较为合理。
3.2 广义Gibson地基Duxseal主动隔振
天然地基的弹性模量会随着深度的增加而逐渐增大,这样的地基称为Gibson地基。土体的剪切模量与深度呈非线性关系[22-23]:
Gs(z)=Gs0+(Gs∞-Gs0)[1-exp(-βz)]
(9)
Gibson地基参数如表3所示。

表3 Gibson地基参数
1)厚度
为了探究不同Duxseal厚度对隔振效果的影响,选取Duxseal的宽度w=6B、埋深t=0.667B,设置Duxseal厚度h分别为0.333B、0.667B、1.333B、2.667B、5.333B。水平向和竖向AR随振源距的关系曲线如图8所示。
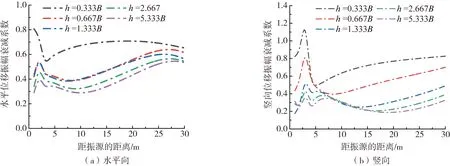
图8 Gibson地基中Duxseal隔振效果随厚度的变化
由图8可知,Duxseal厚度分别大于0.667B和1.333B时,厚度增加所带来的隔振效果增幅较小。从距离来看,水平方向上,隔振效果随着距离的变化先增后减再增,距振源距离l=1 m和10 m时效果最佳,隔振效率均为71 %。竖向的隔振效果明显好于水平方向,最大隔振效率在l=20 m处达到82 %。对于非均匀地基,在近场时隔振效果最佳。当h=1.333B时,水平方向和竖向均有良好的隔振效果。对比Duxseal隔振材料在2种地基中的隔振效果可知,在Gibson地基中埋置不同归一化厚度的Duxseal屏障,其水平向和竖向的隔振表现与均质地基相似。
2)宽度
为了探究不同Duxseal宽度对隔振效果的影响,选取Duxseal的厚度h=0.667B、埋深t=0.667B,设置Duxseal宽度w分别为2B,4B,6B,8B,10B。水平向和竖向AR随振源距的关系曲线如图9所示。
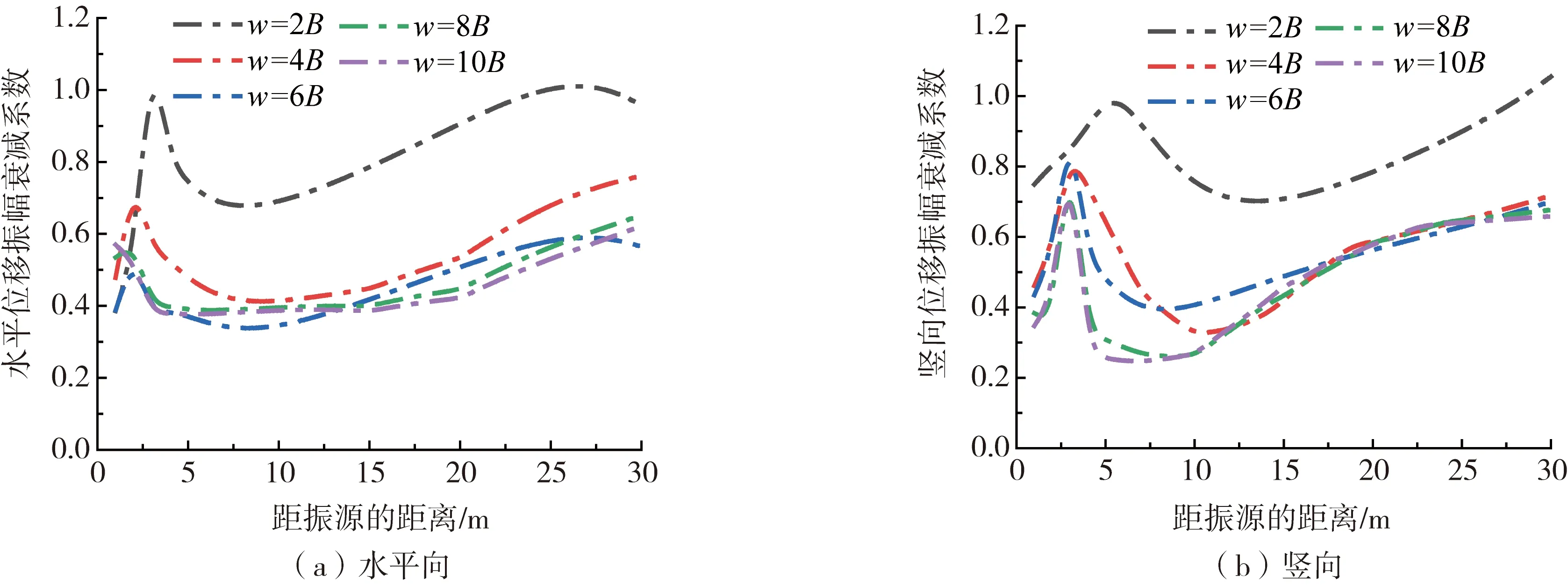
图9 Gibson地基中Duxseal隔振效果随宽度的变化
由图9可知,水平和竖直方向上的隔振效果随着厚度的增加而增大,当w>4B时,此时增加宽度,隔振效果变化较小。从距离上看,当w=2B且l=3 m时,在水平方向上出现振动放大现象。竖向上,l≤5 m时,宽度变化引起的隔振变化较小;5 m 3)埋深 为了探究不同Duxseal埋深对隔振效果的影响,选取Duxseal的厚度h=0.667B、宽度w=6B,埋深t分别为0、0.333B、0.667B、1.333B、2.667B。水平向和竖向AR随振源距的关系曲线如图10所示。 图10 Gibson地基中Duxseal隔振效果随埋深的变化 由图10可知,埋深对水平方向的隔振影响较小;竖向上埋深的变化引起明显的振动起伏。从距离上看,在近场上(l<10 m)不同埋深下都能取得较好的隔振效果,水平向和竖向分别在l=10 m和1 m处效果最佳,达到73 %和86 %;但l>10 m时,距离的增加对隔振不利。因此,在隔振时,Duxseal应选取较小的埋深,且更适用于近场隔振。对比不同归一化埋深的Duxseal屏障在2种地基下的隔振效果可知,Duxseal材料在2种不同的地基中水平向隔振表现相似;对于竖向上的隔振效果,Gibson地基在近场的综合隔振表现更优异。 利用三维半理论半解析边界元法推导了三维薄层法的基本解答,分析移动荷载下均质和Gibson地基中埋置Duxseal的隔振效果,讨论不同Duxseal直径、厚度及埋深对隔振效果的影响。主要结论如下: 1)水平方向上,Duxseal材料在2种地基中隔振效果相差很小;但在竖向上,对比均质地基和Gibson地基,竖向位移振幅衰减系数存在一定的差异。因此,采用Duxseal作为隔振屏障需要着重考虑土质参数。 2)增加Duxseal厚度对振动起到一定的隔振效果,但竖向上会产生较大波动。厚度增加到一定数值(水平向h=0.667B,竖向h=1.333B),此时厚度增加,隔振效果变化幅度较小且趋于稳定。 3)在一定范围内增加Duxseal宽度,隔振效果提升较明显。水平向和竖向隔振效果在距振源5~10 m处均达到最优,但在远场出现振动放大现象。 4)Duxseal埋深对水平向隔振影响较小,竖向上埋深的增加引起较大的隔振效果波动。较小的埋深对振动有利。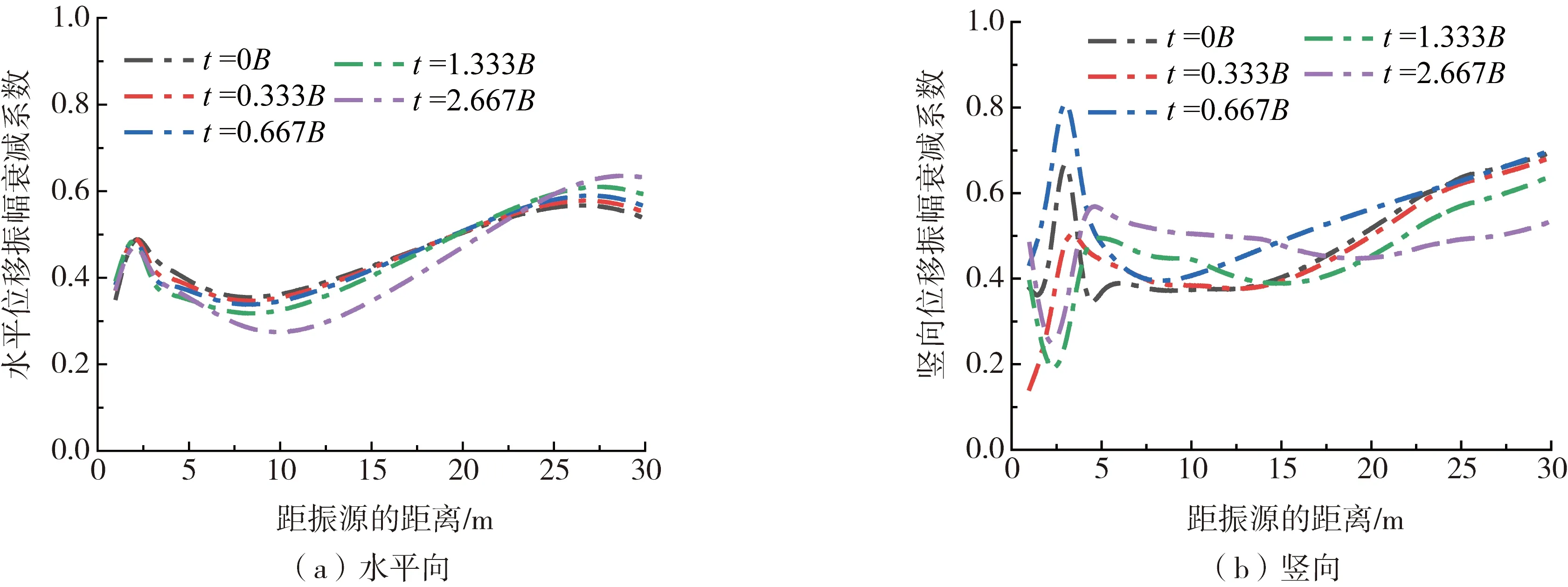
4 结论

