基于混合式蝴蝶算法的局部阴影光伏MPPT研究

张鹏宇，赵晋斌，潘 超，毛 玲，王一鸣

(1.上海电力大学电气工程学院，上海 200090；2.锦浪科技股份有限公司，浙江宁波 315712)

随着“碳达峰”、“碳中和”目标的提出，新能源发电在电力系统建设中的比重不断增大。其中，光伏、风能已成为新型电力系统发电的主流技术。光伏发电技术也存在许多问题亟待解决，诸如能量转换效率低、出力不稳等。这便使得最大功率跟踪(MPPT)技术在工程中得以研究，以实现光伏阵列始终输出最大功率。在实际运行过程中，光伏阵列的出力受实际环境影响，往往处于局部阴影状态。在局部阴影下，光伏阵列会产生热斑效应，导致其输出P-V 特性曲线呈现多峰值现象，此时常规的MPPT 易陷入局部极值点而失效。因此，针对多峰值MPPT算法的研究一直是当前的研究热点之一[1]。

蝴蝶算法(BOA)是Arora 和Singh 于2019 年提出的一种元启发式算法，具有较强的全局寻优能力[9]。但是，在该算法中，蝴蝶种群数目会影响BOA 算法的收敛速度与精度。因此，基于蝴蝶算法，提出了一种混合式的蝴蝶优化算法。通过在BOA 算法中引入爬山法(HC)，首先利用蝴蝶算法进行全局寻优，在搜索到全局最优值附近时切换爬山法来进行最大功率点精确跟踪，缓解元启发式算法中过多初始种群数导致的收敛速度慢、寻优时间长等问题，以此来提高BOA 算法的整体搜索速度。通过仿真实验，验证了所提算法的有效性，能够在多峰状态下以较短的寻优时间成功搜索到全局最大功率，有效提高了光伏发电系统的能量转换效率。

1 光伏电池建模及其输出特性

1.1 光伏电池等效模型

光伏电池作为光伏发电系统中的“源”部分，其本质相当于一个非线性的直流电源。光伏电池的等效模型如图1 所示。

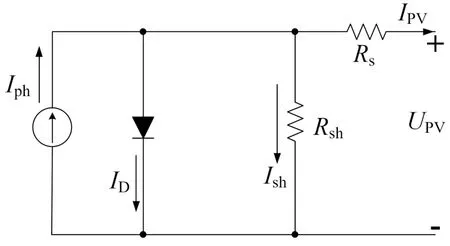
图1 光伏电池等效模型

根据基尔霍夫电流(KCL)定律，可得到光伏电池输出特性方程：

式中：Iph为光生电流；UPV、IPV分别为光伏输出电压和电流；Id为二极管反向饱和电流；q为电子电荷常数，其值为1.6×10-19C；A为光伏电池常数因子，通常取1～2；k为玻尔兹曼常数，其值为1.38×10-23J/K；T为光伏电池的外部环境温度；Nse为串入电池单元数目；Rs、Rsh分别为光伏电池等效串联和并联电阻。

对于光伏发电系统来说，无论是集中式还是分布式，光伏源往往是由串并联形式的光伏阵列组成。因此，由N×M规模的光伏模块串并联而成的光伏阵列，可得到其特性输出方程为：

1.2 局部阴影下光伏阵列输出特性分析

在光伏发电系统实际运行中，由于云层、建筑和太阳辐射角度等现实因素影响，光伏阵列中的光伏单元往往受到的太阳辐照度并不相同，由此便产生了光伏阵列的局部阴影情况。局部阴影会导致光伏阵列产生热斑效应并造成功率失配。为了防止热斑效应导致光伏单元局部温度过高损坏光伏单元，光伏单元需并联旁路二极管Dbypass。局部阴影下的光伏阵列结构如图2 所示。

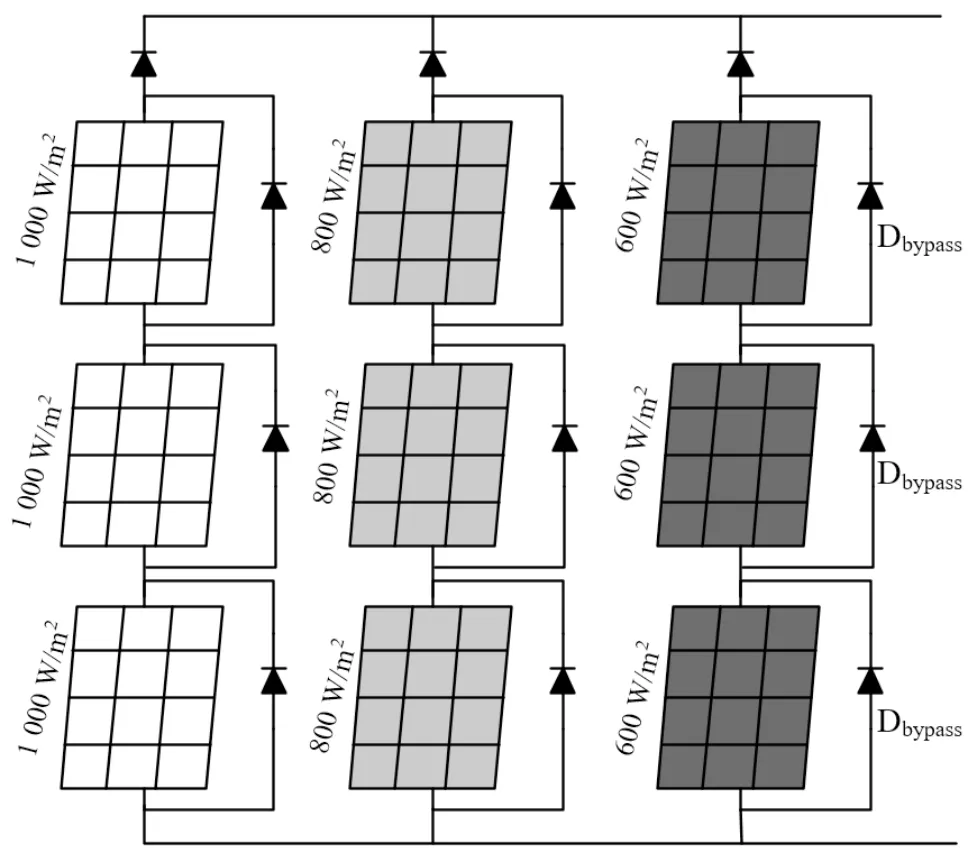
图2 局部阴影下的光伏阵列结构

均匀辐照度下的光伏阵列输出特性与局部阴影下的光伏阵列输出特性如图3 所示。在图3(a)中，均匀辐照度下光伏阵列P-V 特性曲线呈现出一种非线性关系，并且该非线性曲线只包含一个最大功率点(MPP)。

有研究者提倡课堂教学中运用直觉和数学美学启发学生进行创造性思维．张昆提倡教师在解题教学中对任务的数学化信息进行审美意向的过滤与引导，让学生凭借数学的对称美、和谐美与奇异美产生数学直觉与启发，进而探寻问题本质，挖掘“真知”[57]．赵思林等人提倡通过培养学生的数学直觉发展创造力，并提炼出培养数学直觉的若干策略，如优化认知结构，创设直觉思维场情境（问题情境、直观情境、审美情境等），训练直觉思维方法（观察法、联想法、归纳法、类比法、猜想法、估算法等），开发元直觉思维，等等[58]．

图3 光伏阵列输出特性

当光伏阵列受到局部遮光时，由于Dbypass的引入会使光伏阵列的输出特性呈现出一种多峰值状态，如图3(b)所示。而这种P-V 特性曲线包含多个局部最大功率点(LMPP)和一个全局最大功率点(GMPP)，从而导致搜索真正的最大功率点变得十分困难。

2 混合式蝴蝶优化算法在MPPT 中的应用

2.1 蝴蝶优化算法

蝴蝶优化算法是Arora 和Singh 在2019 年根据研究蝴蝶的觅食与交配行为提出的一种元启发式算法。该算法具有较强的全局寻优能力，当蝴蝶在空间飞行时，每只蝴蝶会产生一定浓度的香味fi(t)。其产生的香味浓度公式如下：

式中：fi是第i只蝴蝶产生的香味；Ii是第i只蝴蝶感受到的刺激强度；c是感觉模态因数；α是模态幂指数。

此外，每只蝴蝶感受到自身周围其他蝴蝶的香味，最终朝向香味浓度最大的个体飞去。切换概率用来控制全局搜索与局部搜索。r＞Ps，则进行全局搜索；r≤Ps，则进行局部搜索。蝴蝶的位置更新迭代公式如式(6)～(7)所示：

式中：xi(t+1)为迭代t+1 次的蝴蝶位置；xi(t)为迭代t次的蝴蝶位置；r和Ps为[0,1]的随机数；xbest(t)为迭代t次的最佳位置；xj(t)、xk(t)为第j、k只蝴蝶迭代t次的位置。

2.2 BOA-HC 算法在MPPT 中的应用

BOA 算法虽然可用于搜索多峰值状态下的MPPT，但由于算法寻优能力受蝴蝶种群数影响，较多的初始种群会导致算法运算负担加重，搜索时间变长。而对于多峰值情况来说，在进行全局最大功率跟踪时，每个峰值范围内本质上可看作是单峰搜索。因此，根据上述BOA 算法中的问题与对光伏输出特性的分析，本文利用爬山法的快速收敛性[10]，将其与BOA 算法相结合，提出一种基于BOA-HC 的MPPT 算法。

算法的具体思想为：在局部阴影情况下，BOA 算法首先被用于进行全局寻优，在搜索至GMPP 附近时进行算法切换，由爬山法执行后续GMPP 搜索，直至满足搜索精度要求。

BOA-HC 算法主要步骤为：

第一步：变换器占空比[0,1]区间被视为搜索空间，初始占空比数量视为蝴蝶个数，在搜索空间中线性分布10 只蝴蝶，其相应的空间位置记为Di(i=1,2,3…,10)；

第二步：计算输出功率P=UPVIPV，比较并找到最大功率Pbest并记录此时的最优占空比Dbest；

第三步：在该算法中，将蝴蝶的刺激强度Ii定义为关于功率P的函数，如式(8)所示，并通过式(5)计算出每只蝴蝶产生的香味浓度；

第四步：通过切换概率条件决定算法执行全局搜索还是局部搜索，并根据式(6)～(7)更新每只蝴蝶的位置，即占空比，同时进行记录；

第五步：比较找出更新后的Dmin、Dmax，根据式(9)判断其是否接近满足算法切换要求，若满足，则表明已找到峰值点附近，此时启动爬山法MPPT；若不满足，则重新启动蝴蝶算法；

第六步：为防止由爬山法带来的最大功率跟踪的功率振荡与误判，不再以ΔD为固定步长，而是在固定步长的基础上加入功率变化率以此当作爬山步长，即ΔD=S×(ΔP/ΔU)，其中S取0.001，该修正可随着接近全局最大功率而使爬山步长逐渐减小，增大U，若ΔP＞0，使D=Dold+ΔD，若ΔP＜0，使D=Dold-ΔD；减小U，若ΔP＞0，使D=Dold-ΔD，若ΔP＜0，使D=Dold+ΔD；

第七步：对跟踪功率误差程度|P-Pold|/Pold＜0.05 进行检测判定，以此来判断跟踪的最大功率精度是否满足要求，若满足，则持续将爬山法搜索的占空比输出给变换器；反之，则重启算法重新寻找全局最大功率。

BOA-HC 算法的流程图如图4 所示。

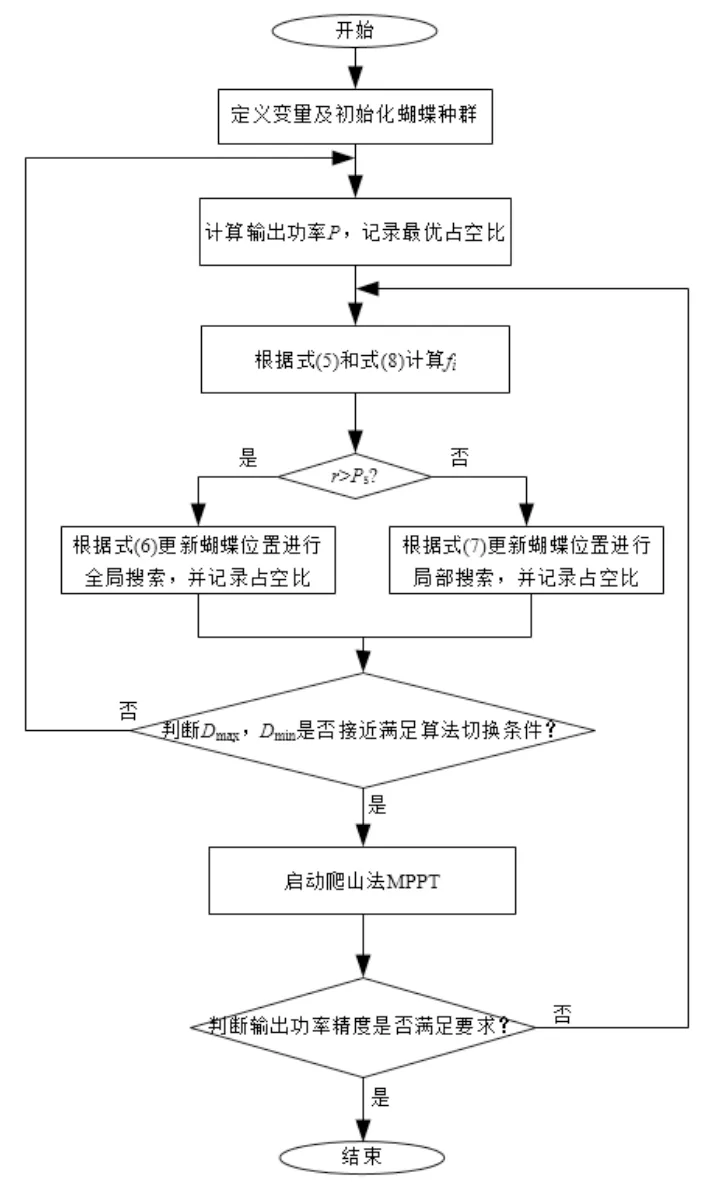
图4 BOA-HC算法流程图

3 仿真验证

为了验证BOA-HC 算法的有效性，在MATLAB/Simulink中搭建了光伏仿真模型。该模型采用5×1 规模的光伏阵列，电路主体结构采用Boost 电路，BOA-HC 算法通过S-function模块编写实现。具体搭建结构如图5 所示，光伏单元参数如表1 所示。

表1 光伏单元参数

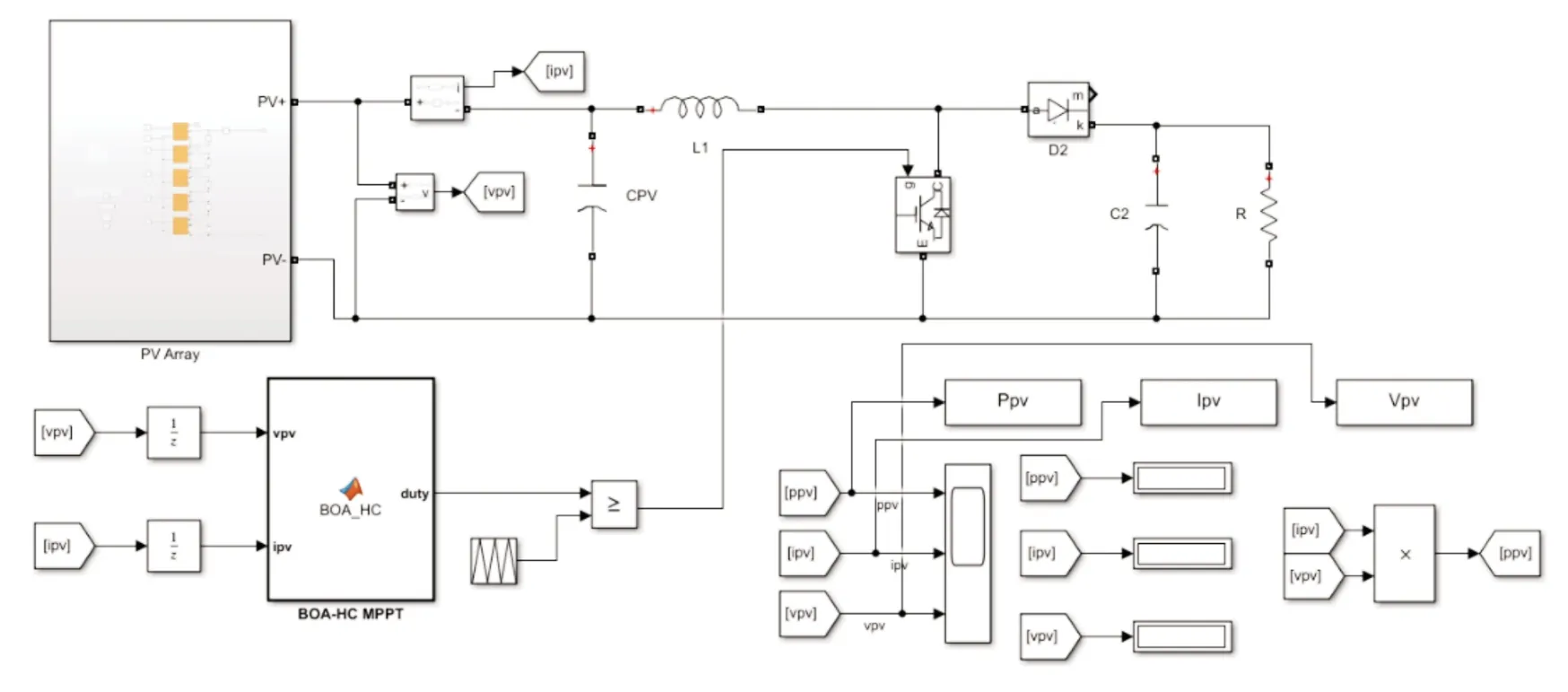
图5 光伏发电系统模型

对光伏阵列设置的环境参数：将5×1 的光伏阵列按顺序定义为PV#1～PV#5，每个光伏组件所受到的太阳辐照度分别 为PV#1 1 000 W/m2，PV#2 1 000 W/m2，PV#3 900 W/m2，PV#4 800 W/m2，PV#5 600 W/m2。本文主要研究光伏阵列发生遮挡时每个光伏组件接受到不同辐照度下的最大功率跟踪情况，并且考虑到实际中环境温度发生大范围局部突变的可能性较小，因此，默认整个光伏阵列所处外部环境温度并无较大变化，外部温度环境统一设置为标况25 ℃下。该测试环境下的光伏阵列输出全局最大功率如图3 所示，GMPP 为4 424 W。以同样种群数目N=10 的PSO 算法和BOA 算法作为对比实验，得到的仿真结果如图6～8 所示。

图6 PSO 仿真结果

分析图6 可知，在相同初始种群下，PSO 算法约在1.4 s 可搜索至稳态，搜索时间较长且输出的平均功率为4 036 W。此外，PSO 算法在达到稳态后存在较为明显的功率振荡。

由图7 可知，在BOA 算法下，该方法跟踪到的输出功率平均值为4 312 W，并在1 s 左右达到稳态，相较PSO 算法，搜索时间降低了28.6%，同时拥有较好的稳态输出特性。

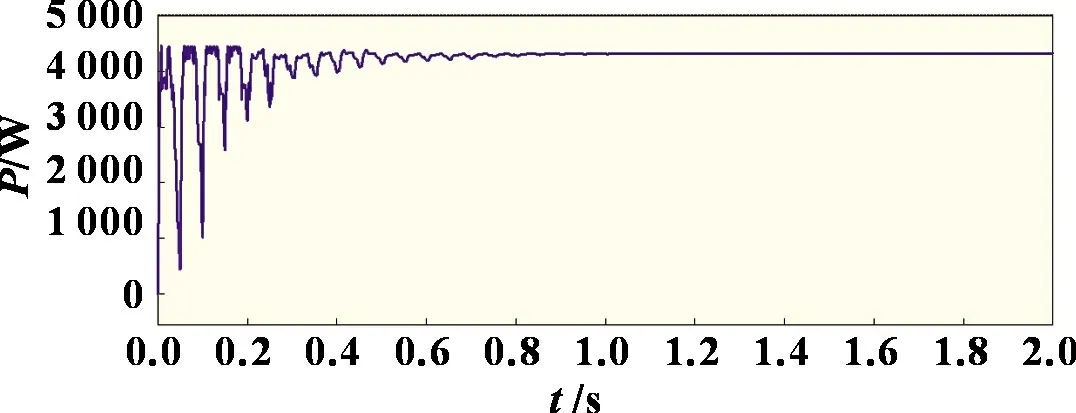
图7 BOA 仿真结果

图8 给出了所提BOA-HC 算法的仿真结果。分析图8 可以看出，加入爬山法后的BOA 算法，其跟踪时间约在0.51 s收敛，与PSO、BOA 算法相比分别缩短了63.6%、49%，跟踪后的输出功率平均值达到4 313 W，并且没有功率振荡情况的产生。

图8 BOA-HC仿真结果

为了能够更加直观看出BOA-HC 方法的性能，对局部阴影下的三种MPPT 方法性能进行总结对比，结果如表2 所示，其中，定义跟踪效率为跟踪功率平均值与最大可利用功率的百分比。

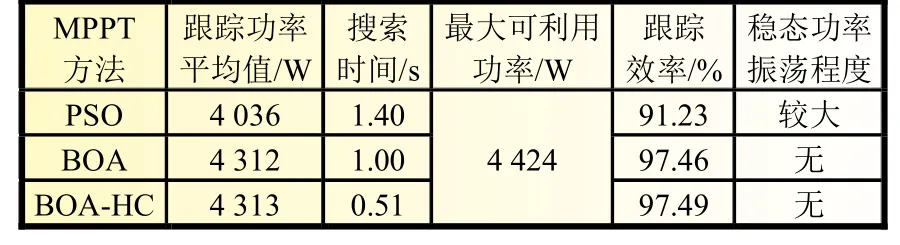
表2 三种MPPT 跟踪方法性能对比

通过表2 可以总结出，相较PSO 与BOA 算法，所提BOAHC 算法不仅使得局部阴影下的平均跟踪功率有所提高，并且搜索速度得到提升，跟踪时间缩短。此外，BOA-HC 算法仍能在保持较好跟踪效率的同时，抑制功率振荡情况的产生。

4 结论

本文针对局部阴影下光伏阵列输出的多峰值特性，提出一种混合式的BOA 算法，即BOA-HC 算法。在局部阴影条件下，将传统爬山法MPPT 引入BOA 算法中。将传统跟踪方法的快速收敛性与元启发式MPPT 算法的全局寻优功能相结合，在保证跟踪效率的同时提高算法的搜索速度。由仿真测试结果可以发现，相较于具有相同种群数的PSO 算法与BOA算法，BOA-HC 的搜索时间更短，并保持了较好的稳态输出功率和跟踪效率，证明了BOA-HC 算法的可行性及有效性，同样，也从侧面证明了传统MPPT 算法与元启发式MPPT 算法结合的优越性。