无速度主动磁悬浮轴承系统全频域不平衡控制
罗浩杰, 刘江, 王斌, 张波涛
(1.武汉科技大学 信息科学与工程学院,湖北 武汉 430081; 2.武汉工程大学 电气信息学院,湖北 武汉 430205;3.武汉科技大学 计算机科学与技术学院,湖北 武汉 430081)
0 引 言
主动磁轴承(active magnetic bearings,AMB)因其具有无机械接触、免润滑、可在高速下长期运行和轴承刚度可调等优点,在高速主轴、离心压缩机及飞轮储能系统等高速旋转机械领域受到越来越多的关注[1-5]。
转子材料特性的不一致以及加工精度和安装误差等因素都会造成转子的质量不平衡,而质量不平衡产生的不平衡力会激起与转子同频的不平衡振动。在高速旋转机械运行时,不平衡振动不但会影响系统对转子的控制精度,严重时甚至会影响系统的安全运行。近年来,国内外学者针对不平衡振动的控制策略主要分为两种:一种为不平衡补偿,迫使转子绕其几何轴旋转,旨在实现“零转子位移”,但转子产生的反作用力会作用于底座上,并且高速运行下容易导致功放电路饱和;另一种为自动平衡,迫使转子绕其惯性轴旋转,旨在实现“零电流或零振动力”,这种方法可以显著降低不平衡力,并避免功放电路饱和,因此也受到了更多研究人员的关注,最小均方(least mean square,LMS)算法[6]、同步旋转坐标变换[7]、广义陷波器[8]、重复控制[9]、自适应强制平衡[10]等控制算法被相继提出。
上述算法均需要转子的角频率反馈才能实现,在实际中通常由霍尔传感器、光电编码器等获得,然而,测速传感器在许多应用中都存在一些限制,包括机械安装困难、机器尺寸有限等问题,且一旦测速传感器存在较大误差或发生故障时,控制系统将无法获得准确的转速信号。因此,需要在转子不平衡信号中估计转子的实际转速。针对磁悬浮转子的角频率估计问题,Lee等[11]提出了角位置微分来估计转子转速,但该方法很容易引进噪声。张染等[12]将转子位移信号中的高倍频分量通过Hilbert变换进行经验模态分解,从而通过Hilbert谱分析得到转速信号,该方法虽然精度有所提高,但倍频分量在低速时不稳定,势必影响转子系统全频范围下的稳定运行。刘虎等[13]根据已知的位移信号和转速信号构建反向传播(back propagation,BP)神经网络模型,并通过参数调整达到良好的测速精度,但该方法过度依赖转子系统的初始位移和转速数据,且计算量较大。Chen等[14]利用磁轴承x和y方向位移信号正交且振幅相等来估计频率,但x、y两方向位移由于安装误差等原因并不时刻满足相互正交和振幅相等,且该方法无法保证转子低速旋转时的系统稳定性。Liu等[15]针对文献[14]方法低速段失稳的问题,在原有自适应陷波器结构上加上了相移角,但x、y两方向位移信号相位和振幅的误差势必会对算法的补偿效果造成较大的影响。
二阶广义积分-锁频环(second order generalized integrator-frequency locked loop,SOGI-FLL)已广泛应用于频率估计和相位锁定领域中,包括电网同步信号提取[16-18]和永磁同步电机的速度估计[19-20]。本文将SOGI-FLL引入主动磁轴承转子系统的角频率估计应用中,构建基于改进型SOGI-FLL(enhanced SOGI-FLL,ESOGI-FLL)的主动磁轴承转子系统同步振动力抑制方法,在反馈控制的基础上增加位移前馈补偿环节,以获取更好的振动抑制效果。然后,利用根轨迹法分析加入SOGI-FLL的主动磁轴承转子系统的稳定性,并基于此设计变增益系数,实现嵌入SOGI-FLL的磁轴承转子系统低速旋转时的系统稳定。最后,通过仿真分析验证该方法的可行性。
1 磁悬浮转子不平衡扰动模型
AMB转子系统模型如图1所示。转子轴向自由度由永磁轴承所约束,径向的4个自由度分别由左右的2个电磁轴承约束。转子的最大转速远小于一阶弯曲模态频率,因此以下建模分析都只考虑转子的刚性模态。设O-xyz坐标系为转子中心平面对应坐标系。
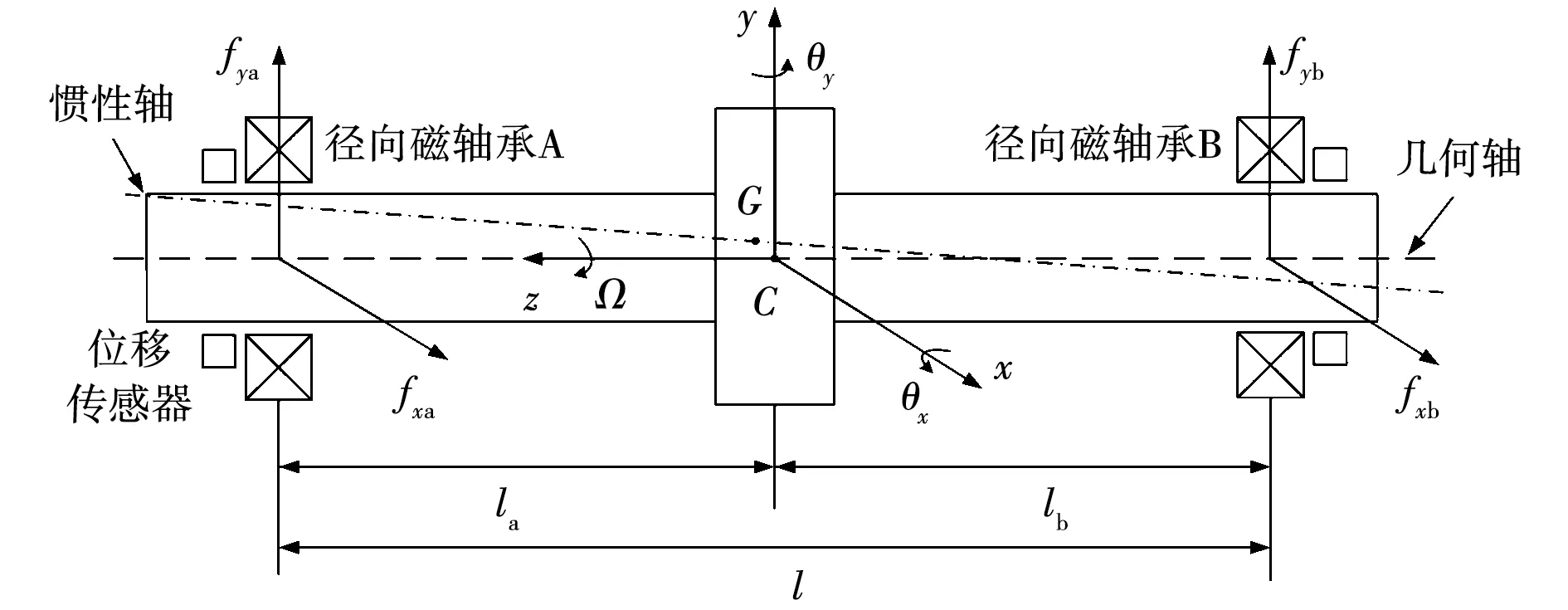
图1 四自由度AMB刚性转子系统结构图Fig.1 Structure of 4-degree-of-freedom AMB rotor system
设转子的质量为m,la和lb分别是左右两端径向磁轴承所在平面到C点的距离,l是左右两端磁轴承所在平面之间的距离,J为转子绕x、y轴旋转的转动惯量,Jz为转子绕z轴旋转的转动惯量,xa、ya和xb、yb分别是两端位移传感器测得的磁轴承径向位移,则转子几何中心处的位移和转动角度为:
(1)
为了便于分析磁悬浮转子系统的运动方程,特做如下假设:1)转子为轴对称转子,两端的AMB结构参数都相同;2)位移传感器与AMB在转子轴向位置重合。
根据牛顿第二定律可得径向四自由度转子的运动微分方程为:
(2)
式中:fxa、fya和fxb、fyb分别为左右两端磁轴承产生的电磁力;fx和fy为干扰力。
为了便于分析不平衡下的转子动力学模型,取转子截面建立坐标系,如图2所示,转子几何中心C和质心G不重合。设转子几何中心C在固定坐标系O-xy中的坐标为(xc,yc),质心G在固定坐标系O-xy中的坐标为(xg,yg),Ω为转子的转速。
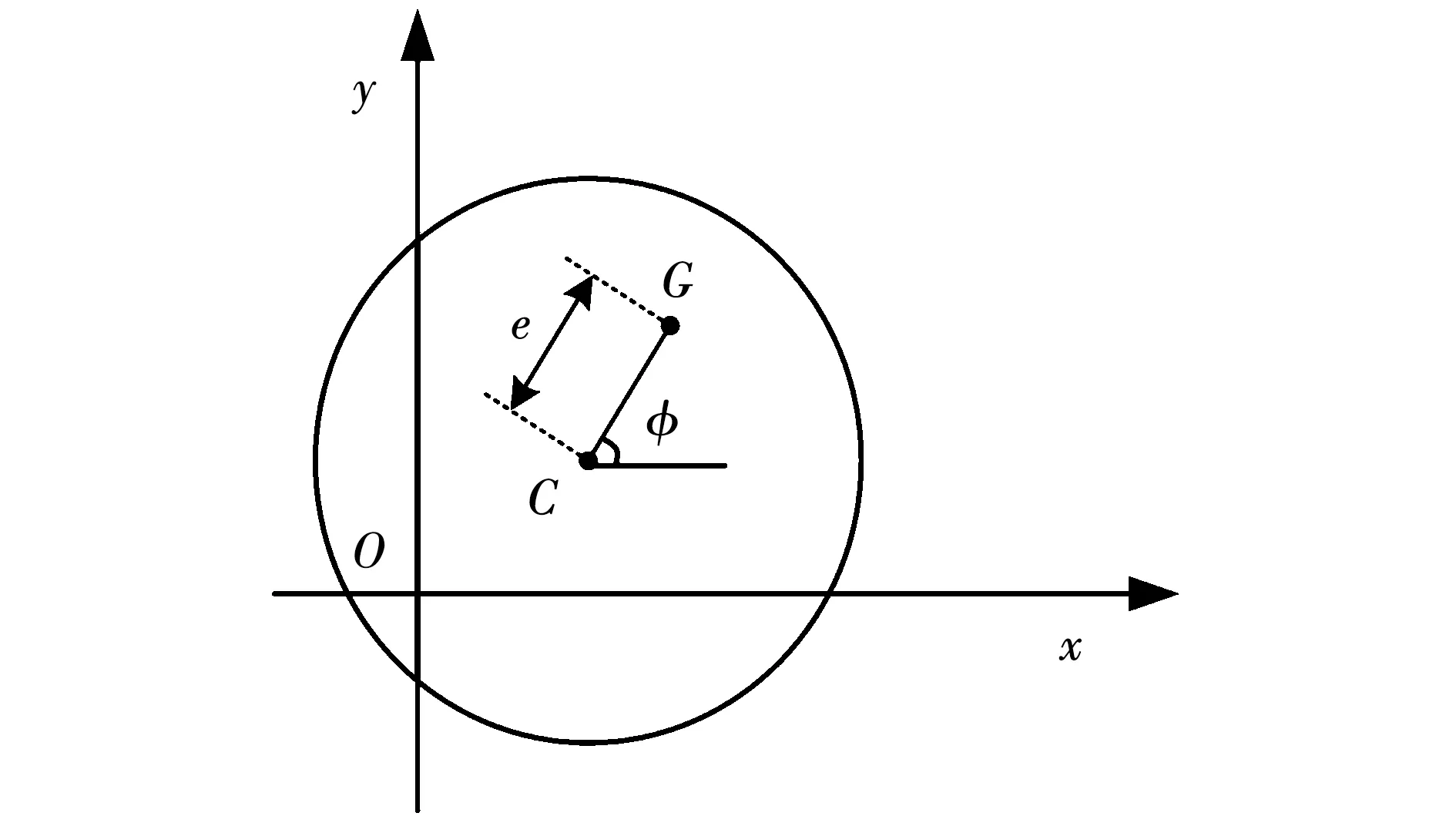
图2 转子截面示意图Fig.2 Schematic diagram of rotor section
转子质心与几何中心坐标之间的关系可以表示为:
(3)
式中:e为转子的偏心距;φ为转子旋转角度。
将式(3)代入式(2)可得转子不平衡力在x,y轴上的分量为:
(4)

结合式(2)和式(4)可得含不平衡量的转子系统运动微分方程为:
(5)
式中ez为质心G在oz轴上的投影。
2 基于ESOGI-FLL的全频域自动平衡控制
2.1 基于SOGI-FLL的振动信号角频率辨识
图3为SOGI-FLL的结构框图,其主要由SOGI-正交信号发生器(SOGI-quadrature signal generator,SOGI-QSG)和FLL两部分组成。

图3 SOGI-FLL结构框图Fig.3 Structure of SOGI-FLL
由图3可知,SOGI-QSG的状态空间方程可以表示为
(6)
式中:k是一个常数;u1=Asin(Ωt+δ),A为输入信号的幅值,δ为初始相位;Ω为转子角频率。
由式(6)可知,从输入信号u1到输出信号x1和x2的传递函数为
(7)
令s=jω,当k≠0时,式(7)可以表示为:
(8)
式中ΔΩ是一个很小的值,且其值远小于Ω。
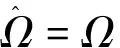
FLL估计频率可由反正切函数得到,其表达式为
(9)
(10)
将式(10)代入式(9)中,可得
(11)
式中γ是一个恒为正的收敛因子。
式(11)说明FLL频率估计的收敛性与两相输出幅值的平方和、输入信号频率和SOGI-QSG的增益都有关,那么图3中将增益归一化后,FLL的频率估计特性就只与一个参数γ有关,简化了后续的参数设计。
结合式(6)和式(11)可得,SOGI-FLL的状态方程可以表示为:
(12)
图4为加入SOGI-FLL的磁轴承转子系统的同步电流控制框图。

图4 磁轴承转子系统的同步电流控制框图Fig.4 Block diagram of synchronous current control for AMB-rotor system
2.2 基于ESOGI-FLL的无速度同步不平衡振动力控制
AMB转子系统的同步振动力可以表示为
F=Fi+Fx=kii(xa)+kxxa。
(13)
式中:xa表示转子位移;i(xa)表示电磁线圈的电流,是xa的函数。转子位移xa中存在与转速同频的不平衡振动,因此Fi和Fx中都存在与转速同频的分量。
由于同步电流的抑制只消除了电流刚度力Fi,磁轴承转子系统中仍然存在位移刚度力Fx。为了最大程度地抑制不平衡振动,在图4的基础上增加位移刚度力前馈补偿模块,实现同步振动力的抑制,如图5所示。

图5 基于ESOGI-FLL的磁悬浮转子同步不平衡振动力控制Fig.5 Synchronous unbalance vibration force suppression of AMB-rotor system using ESOGI-FLL
对式(13)进行Laplace变换,可得
kiA(s)C(s)[Gs(s)xa(s)-x1(s)]。
(14)
当基于SOGI-FLL的陷波器能正确跟踪锁频时,可得x1=Gs(s)d,那么式(14)可以改写为
F(s)=[kx+kiA(s)C(s)Gs(s)][xa(s)-d(s)]。
(15)
从式(15)可知,增加位移前馈环节后,同步振动力抑制为0,实现了刚性转子的自动平衡。基于ESOGI-FLL的磁悬浮转子系统同步振动力控制方法如图5所示,其等效框图如图6所示。图5中,ε0为增益系数。
由图3可知,二阶广义积分器u1到e的传递函数可以表示为
(16)
令s=jω且k≠0时,式(16)可改写为:
(17)
式中ΔΩ为二阶广义积分器的带宽,其值只与增益k有关。
图7为不同增益k下二阶广义积分器的频率特性。由图可知,二阶广义积分器效果实际上与陷波器类似,且带宽随着增益k的增大而变大。
主动磁轴承采用PID控制,其传递函数可以表示为
(18)
式中:kP为比例系数;kD为微分系数;kI为积分系数。
功率放大器的传递函数可以看作是具有放大系数的零阶系统,即A(s)=ka,而位移传感器则不考虑其动态特性,将其视为比例环节,即Gs(s)=ks。
由图3可知,二阶广义积分器中e到x1的传递函数可表示为
(19)
2.3 无速度闭环控制系统稳定性和性能分析
由图6可知,主动磁轴承-转子系统的闭环特征方程为
(20)
将式(16)、式(18)和式(19)代入式(20),整理可得
ms5+(Ωmε0k+kakskikD)s4+(Ω2m+kakskikP-kx)s3+[kakskikDΩ2-Ω(kkx+kkxε0)+kakskikI]s2+Ω2(kakskikP-kx)s+Ω2kakskikI=0。
(21)
令
(22)
那么式(14)可以表示为
ms5+a1s4+a2s3+a3s2+a4s+a5=0。
(23)
根据劳斯判据可知磁悬浮控制系统稳定的充要条件为:
(24)
由式(24)可知,系统稳定的充要条件与开关ε0和转速Ω有关。为了说明AMB转子系统的稳定性,以Ω(rad/s)为变量,分别绘制了ε0=1和ε0=-1时,1~500 Hz(步长为5 Hz)范围内转子系统的闭环根轨迹,如图8所示。
由式(24)和图8(a)分析可得,当ε0=1时,当转子转速低于86.1 Hz时,系统具有右半平面的极点,系统不稳定;当转速高于86.1 Hz时,系统闭环根轨迹通过虚轴进入左半平面,系统稳定。可见,在基于SOGI-FLL的不平衡控制方法中,转子系统无法在比刚体临界转速低的速度下稳定运行。
由图8(b)分析可得:当ε0=-1时,当转子角速度低于116.1 Hz时,系统的闭环极点均位于虚轴左半平面,系统稳定,但高于116.1 Hz时,闭环根轨迹进入虚轴右半平面,导致系统不稳定。磁悬浮刚性转子的临界转速区域为86.1~116.1 Hz。
由式(16)可知,增益系数ε0的大小没有改变基于SOGI-FLL的陷波器传递函数的零点,因此算法对同步电流仍有抑制作用。
基于以上的转子系统稳定性分析,本文提出变增益系数的方法来实现全转速范围下的转子系统自动平衡控制,即分别在转子亚临界转速以下和超临界转速以上取ε0=1和ε0=-1,利用变增益系数方法后,闭环系统的根轨迹如图9所示。由图可知,系统的所有闭环极点都位于虚轴的左半平面,从而能够在全频范围内实现稳定运行。
3 仿真结果与分析
为了验证该方法的可行性和有效性,在MATLAB/Simulink中搭建了主动磁轴承转子系统,并进行了仿真验证。AMB转子系统的各项物理参数见表1。
3.1 恒定转速仿真
基于上述的稳定性分析,分别在转子的亚临界转速以下和超临界转速以上进行仿真。在0.3 s时加入本文提出的算法,转子A端的估计频率、位移和同步振动力的仿真结果如图10所示。
结果表明,图10(a)中,在0.3 s启动算法后,估计频率在0.31 s后收敛到给定的频率值,且在给定频率处上下震荡,误差在0.21 Hz以内,转子的位移也能快速被抑制,转子的同步振动力几乎收敛到0;图10(b)中,频率估计的时间为0.228 s,且误差在0.12 Hz以内,转子的位移和同步振动力均能被快速抑制。因此,本文算法在频率的估计、转子位移和同步振动力的抑制都有较好的效果。
在实际的磁悬浮转子系统工况下,自身设备噪声会导致转子的位移信号中含有一定的噪声,噪声通常会影响系统的运行。为了研究噪声对算法补偿效果和频率估计的影响,在转子旋转频率150 Hz的条件下,加入信噪比SNR为20、10的高斯白噪声。启动自动平衡控制前后,不同噪声下转子A端的仿真结果如图11所示。

图11 不同噪声下转子A端的仿真结果Fig.11 Simulation results at A side with different SNRs
仿真结果表明,加入一定的噪声干扰后,算法的补偿效果受到了较大的影响。由于同频振动力抑制算法只对同频的振动信号起作用,噪声信号并没有受到影响,因此信噪比越低补偿效果也变得越差。但是,噪声干扰并没有对系统的收敛性能产生影响,转子的同步振动力和同步位移依然能够快速被抑制。频率的估计轨迹随信噪比的降低而变得曲折波动,但在信噪比10 dB下,频率估计误差也在0.79 Hz以内,并且能逐渐收敛至目标值,这也证明了该算法具有一定的自适应能力和抗干扰能力。
3.2 变转速仿真
前述已经验证了本文算法在恒定转速下的频率估计特性和不平衡补偿效果,为了研究该算法在转子变转速下的补偿效果和频率跟踪的有效性,在转子加速度α=30π rad/s2的条件下进行了仿真。图12表示在变转速条件下算法的频率跟踪曲线,其中虚线和实线分别表示算法的估计频率值和实际的参考频率值。

图12 变转速条件下算法的频率跟踪曲线Fig.12 Frequency tracking curve of the algorithm under variable speed conditions
由图12可知,估计频率在大约0.9 s时收敛到参考频率,且误差在0.3 Hz内。因此,本文算法在变转速条件下仍然具有良好的频率估计性能。
图13分别给出了算法前后转子A端同步振动力和同步位移的响应结果。仿真结果表明,相比于没有加入振动抑制算法的转子同步振动力和同步位移,施加振动控制后,转子的振动力和位移的幅值都大幅减小。在加入振动控制前,转子的振动位移和振动力都很大,其峰值分别达到了0.185 mm和147 N,而在加入算法后,转子位移峰值和振动力峰值降低至0.002 56 mm和2.3 N,不平衡响应的抑制效果明显。
4 结 论
本文提出了一种改进的带增益系数自适应频率估计滤波算法来抑制不平衡同步振动力,解决了加入SOGI-FLL后导致磁轴承转子系统低速段失稳的问题。该方法仅通过一路转子径向位移信号实现了转子旋转频率的估计,在线跟踪同频率信号,自适应补偿不平衡,最后引入增益系数实现了全频域范围内转子系统的稳定运行。该方法可以同时估计转子的旋转频率和抑制同步振动力,且结构简单易于实现。最后,仿真结果验证了所提出算法在全频域范围内同步振动力抑制的有效性和自适应特性。

