整体把握明思路 系统整合提效率——以“常见数量关系”板块为例

文| 魏军君

单元整体设计是提高课堂教学效率的重要方法。众所周知，小学数学教材由一个个相对独立的单元构成，同一单元中的新知又是按照一定的逻辑顺序编写的。因此，教学中应从单元整体设计的视角来审视单元内的课时教学内容，并通过适当的调整与重组来更好地构建起基于学生认知规律与数学学科逻辑的单元教学体系，从而促进教学效率的提升。

一、单元结构介绍与重组

《三位数乘两位数》是在两位数乘两位数的基础上学习的，主要内容包括：三位数乘两位数的笔算、积的变化规律、常见数量关系。

第一个板块是例1、例2，即“三位数乘两位数”笔算乘法，两个例题按一般到特殊的形式编排，即例2一般是在例1“三位数乘两位数笔算”的基础上，学习因数末尾有0 或第一个因数中间有0 的两种特殊的乘法笔算；第二个板块是例3，即积的变化规律，通过计算有联系的乘法题组，观察、分析、概括出规律；第三个板块是例4、例5，即乘法中两个常见的数量关系，通过举例，概括得出更为一般的数量关系。

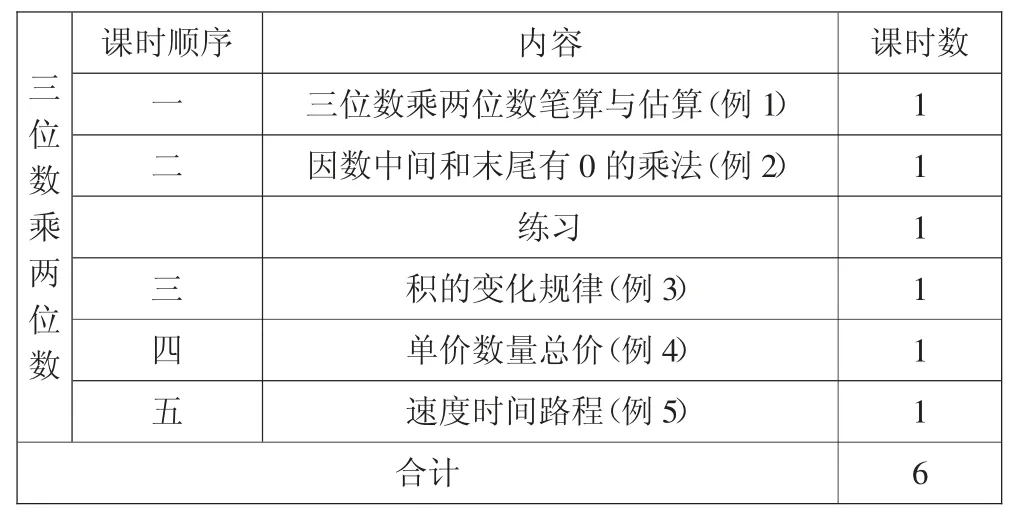
原编排序列与课时安排

对于教材的编排，在实际教学中我们有以下几点思考：

1.这个单元是整数乘法的最后一个单元，要凸显总结整数乘法笔算与估算的一般方法，例1 笔算和估算需要进一步加强。

2.例2，160×30 简算的依据是例3 积的变化规律，而例3 被安排在例2 后面教学，算理依据滞后；建议例3 前移至例2 之前教学，更有利于例2 算理的总结与理解。

3.整个小学阶段，对于“工作效率×工作时间=工作总量”没有安排例题教学，但在实际应用中却很普遍，需要补充教学；而且“速度×时间=路程”这组数量关系安排单薄，需要进一步加强。

通过单元内部结构的重组，增强板块间的内在联系，体现单元的结构性与逻辑性。

调整后的序列及课时安排：

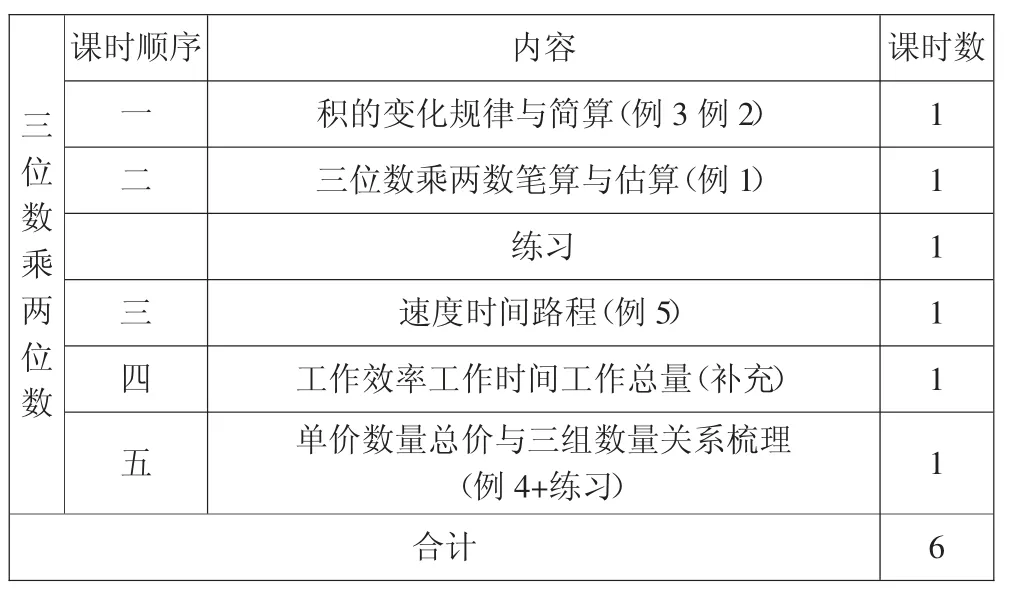
三位数乘两位数课时顺序 内容 课时数一积的变化规律与简算（例3 例2）1二三位数乘两数笔算与估算（例1）1练习 1三速度时间路程（例5）1四工作效率工作时间工作总量（补充）1五单价数量总价与三组数量关系梳理（例4+练习）1合计 6

调整后的单元序列是：积的变化规律→三位数乘两位数→常见的数量关系。总课时没变，例3 和例2整合为一节课，增加了工作效率一节课，把速度提到数量关系板块的第一节课。通过单元板块间逻辑关系的辨析，力争使各个板块之间的逻辑关系更加密切，让原来相互独立的板块，通过合理调整，成为更有逻辑关系的单元学习序列。

二、学情实证，审视学生立场

1.常见的数量关系板块介绍与重组

在日常生活中，“单价”“速度”“工作效率”的数量关系都很常见，但是教材里没有工作效率的教学内容，这里增加工作效率的教学很有必要，也为高段的工程问题进行铺垫。

速度×时间=路程这组数量关系需要进一步加强。速度这节课在此板块中是核心概念，学生理解了速度的含义，对于后面学习单价和工作效率具有指导意义，所以速度这节课放在了这一板块的第一课。第二课时的工作效率，可以看成有关“速度”的数量关系的变式，在学生学习了有关“速度”的数量关系后，添加有关“工作效率”的关系式来解决问题，让学生在比较中总结出有关“工作效率”的数量关系，通过知识的迁移，帮助学生建立工作效率的数学模型。

脱离了速度来研究工作效率是不完整的。速度和工作效率含义相近，学了速度，学生可以迁移到工作效率。我们对速度和工作效率分别进行了前测，看看学生对于它们了解多少，以便准确定位，同时指导工作效率这节课的教学。

2.前测分析与启示

对四年级2 个班82 名学生进行前测。

●第一题：关于速度，你听说过吗？

调查统计如下：

知道的有43.9%，有点知道的有45.1%，听说过的有4.9%，不知道的有6.1%。

一共有93.9%的同学认为知道速度，占了绝大部分。速度这个词在生活中运用得非常广泛，学生很熟悉，家长可能每天都说做作业速度要快一点，生活中经常比赛看谁的速度最快等等。

关于工作效率，你听说过吗？调查统计如下：

知道的有26.3%，有点知道的有34.2%，听说过的有18.4%，不知道的有21%。

一共有79%的同学认为知道工作效率。虽然工作效率在生活中也在用，但是没有速度那么广泛，而且这个概念明显比速度更抽象。还是有大部分学生自认为了解工作效率。那么学生对这两个量的表述水平怎样？于是有了第二题。

●第二题：想一想什么是速度？把你的想法写下来。

调查统计如下：

我们把调查结果分成4 个水平：

水平0：表述错误，占7.3%。对速度的理解是不准确的。

水平1：速度就是时间占14.6%。生活中往往做一件事情比赛谁做得快，用时最少就是最快，所以造成的错觉就是时间就是速度。

水平2：速度表示快慢占74.4%。这一水平是最多的，做事情的快慢就是速度。其中有43.9%的学生认为快就是速度。

水平3：表述中有路程和时间两个量，占3.7%。

看来学生自认为了解的速度但并没有理解速度的真正含义，与自我感觉相差较大。

教学启示：学生对速度的感知。

（1）学生感知到速度表示运动的快慢。

（2）学生对快慢的理解更多停留在时间上。（时间少就是快，时间多就是慢）

教学要思考的重点：

如何让学生经历一个量（速度）的产生过程，从而知道它的意义以及所适用的范围，最终抽象出数量关系。

在教学完速度之后进行了工作效率的前测：

想一想什么是工作效率？把你的想法写下来。调查统计如下：

工作效率相对比较陌生，很多学生不知道如何表达，有85%的学生表述不清楚，有15%的学生表述相对准确。

教学启示：工作效率比速度更抽象，更难表述，但从前测来看，准确表述速度的有3.7%，准确表述工作效率的有15%，相比有了提高，我想这可能是速度的教学对工作效率概念的理解有帮助，迁移到对工作效率的理解。

●第三题：请完成下面各题。

这节课的核心环节就是出示的6 道题目，我们对这6 道题进行了前测，想了解学生对题目中数量关系的理解程度。统计如下：

准确率如下：

（1）第一题81.6%，第二题94.7%，第三题86.8%，第四题81.6%，第五题97.4%，第六题94.7%。

（2）请把6 道题目分类，说一说分类的理由。

分析：有21%的学生按照数量关系来分类，能发现题目中的数量关系进而归类，只是在表述的时候把求一份的工作量也就是求工作效率说成是求速度或者平均数，在学习工作效率之前，速度可能就代表了工作效率的本质。

那么在其他分类中出现的情况又是怎样？有63.3%的学生是按照除法和乘法的情况来分，占了大部分，还有些学生是按照问题分类。

教学启示：本环节引导学生从具体教学情境中认识、探索工作效率、工作时间和工作量三者间的数量关系。通过学生独立思考与同桌互助学习的机制，运用分类、归纳的策略，让学生体验从具象表述到抽象建模的过程。

三、教学启示与思考

由跑得多快到做得多快，由速度转向工作效率，两个量的实质是一样的，学生经历了速度的产生过程，自然而然由速度迁移到工作效率，所以速度这节课对于工作效率有点种子课的感觉。鉴于以上调查，给了我们以下启示与思考：

1.这节课的思考

构建生活具体问题抽象出工作效率的数学模型，并将数学模型用于现实中的简单问题中去。通过不同情境的问题解决丰富工作效率的内涵，让学生从问题解决中建立工作效率、工作时间、工作总量的数学模型。模型思想作为一种数学思想，要真正使学生有所感悟，需要经历一个过程：让学生建构后去运用模型经历问题解决，在此过程中完善自己的认知结构、感悟解决问题的策略，深化认识。

2.单元序列的思考

本单元三个板块相对独立。常见的数量关系这一板块能否上移到第二板块，三位数乘两位数的板块放在最后。因为例1 是关于速度的解决问题，如果在学了速度之后教学，可以用“（火车的）速度×时间＝（到北京的）路程”来概括，前后知识的逻辑关系就更加紧密了。