基于均匀B样条曲线的移动小车路径规划方法

柴 松 马社祥 李 啸

1(天津理工大学电气电子工程学院 天津 300384)

2(天津理工大学计算机科学与工程学院 天津 300384)

0 引 言

为了满足人们对生活便利和生活质量的追逐,无人车、服务型机器人、消防救援机器人等应用逐渐进入日常的生活。移动机器人路径规划是机器人研究领域的重要组成部分,是指在未知环境中,根据给定的指标(经过路径最短、花费时间最少、距离障碍物最远),寻找一条从初始状态到目标状态最优或者近似最优的无碰撞路径。移动机器人路径规划问题是一种典型的NP-hard[1](非典型性多项式困难)问题,针对移动机器人路径规划[2],传统的方法主要有模拟退火算法[3]、人工势场算法[4]、模糊逻辑算法[5]、栅格算法等。栅格算法适用于结构简单的环境中,当空间结构变复杂时,存在计算效率低、存储空间大的问题;模拟退火算法存在计算量大、效率低等问题。随着环境复杂程度的增加,出现了免疫算法[6]、遗传算法[7]、人工鱼群算法[8]、A*算法[9]、神经网络算法[10-11]等,这类算法在移动机器人路径规划取得了显著的成果。

近年来基于B样条曲线的方法也逐渐应用于移动小车的路径规划中。张敬寒等[12]提出一种基于扩大搜索邻域A*算法的平滑路径规划算法,该算法扩大A*算法当前节点搜索邻域范围,采用三次均匀B样条曲线规划路径的平滑处理,有效消除了原规划路径上的路径尖峰拐点。刘紫燕等[13]提出一种改进RRT算法的室内移动机器人路径规划算法,该算法采用目标偏向策略和气味扩散法来改善扩展节点的选取,选取基于三次B样条曲线的路径平滑方法,极大地提升了搜索效率和路径质量。目前路径规划技术仍有两个关键技术有待解决。首先,在时间和计算资源有限的情况下,移动小车行进过程中,安全性能是首要考虑因素,不仅和环境地图中的障碍物无碰撞,而且需要保持相对安全距离。其次,移动机器人在未知环境中移动,应该在很短的时间内不断地重新规划路径,避免在紧急情况下碰到障碍物。

本文针对以上的问题,提出一种基于均匀B样条曲线的移动小车路径规划方法。首先,和上述算法不同的是,前端本文选取控制空间中离散化加速度控制变量作为扩展节点,确保移动小车的速度的连续性,消除初始路径的尖峰拐点使得初始路径平滑。然后,采用软优化的方式,结合环境障碍物的距离信息、路径的平滑度和移动小车的速度、加速度信息优化均匀B样条曲线的控制点,使得均匀B样条曲线的控制点远离障碍物。应用均匀B样条曲线[14]的凸包性质(均匀B样条曲线恒位于其凸包之内),保证移动小车路径更加安全。最后,优化控制点和时间分配关系,确保速度和加速度在可控范围内。

1 路径搜索

本节的前端路径搜索方法是选取控制空间中离散化加速度控制变量作为扩展节点,将移动小车的控制成本和启发式搜索成本相结合,在室内环境地图中计算出耗时最少、控制成本和启发式搜索成本最小的无碰撞初始路径。

1.1 路径生成

移动小车行进过程中,系统位置状态是由二维路径坐标多项式组成,如式(1)和式(2)所示。

p(t)=[px(t),py(t)]T

(1)

(2)

为了简化符号,v(t)=p′(t)表示系统的速度,u(t)=p″(t)∈U=[-umax,umax]2⊂R2表示系统控制输入,X(t)=[p(t)T,v(t)T]T∈R4表示系统的状态向量。状态空间模型如式(3)所示。

X′(t)=AX(t)+Bu(t)

(3)

状态方程的通解如式(4)所示。

(4)

给出初始位置信息p(0)=[px(0),py(0)]T,初始速度信息v(0)=[vx(0),vy(0)]T和控制输入u(t),根据式(4)计算出移动小车行进过程中的路径p(t)。

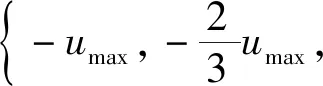
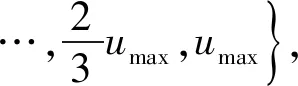
图1 N段分段多项式路径

(5)

1.2 碰撞检测

碰撞检测是路径搜索中必不可少的一部分,它作用是判定移动小车行进路径是否和环境地图中的障碍物发生碰撞,筛选出可以通行的初始路径。本节给定的一组初始状态、控制输入和持续时间,在时间t∈[0,τ]中,满足式(6)。

(6)

式中：Pfree表示无障碍物可通行的自由空间;v(t)是时间t的多项式函数,只需要计算在时间周期[0,τ]内v(t)的极值和阈值相比较。当多项式函数的阶数小于等于5时,很容易求解在闭合区间上的极值。

为了确保路径的安全可行性,本节选取沿着路径遍历的一组位置进行验证如式(7)所示。

P={p(ti)|ti∈[0,τ],i=0,1,…,I}

(7)

对于所有的i∈{0,1,…,I},使得p(ti)∈Pfree,即视为该路径没有碰撞到障碍物,离散化路径点的数量如式(8)所示。

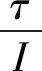
(8)

式中：R表示占用网格的分辨率。式(8)的条件确保两个连续的采样路径点之间的最大距离不超过网格的分辨率,保证移动小车行进过程中无障碍物碰撞。

1.3 成本函数

移动小车行进过程中,通常有多条路径可以到达目标位置,引入成本函数的目的是在多条可到达目标位置的路径中选择一条无碰撞冲突、移动成本和启发式成本最小的初始路径。

路径的移动成本定义为控制输入2-范数的平方加上时间成本,如式(9)所示。

(9)

式中：ρ是时间T的权重值。因为在持续时间τ上的控制输入是定值,所以在持续时间τ路径成本如式(10)所示。

(10)

则从开始状态到终点状态最优路径的实际成本如式(11)所示。

(11)

本节设计了启发式函数加快搜索算法的速度,通过应用庞特里亚金最小原理(Pontryagins Minimum Principle PNP)来计算当前状态Xc到目标状态Xg的启发式成本HC(t),如式(12)所示。

pi(t)=ai3t3+ai2t2+ai1t+ai0

vi(t)=3ai3t2+2ai2t+ai1

ui(t)=6ai3t+2ai2

ai0=pic,ai1=vic

(12)

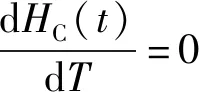
2 B样条路径优化

移动小车行进过程中,前端路径搜索产生的路径可能是次优的。由于忽略了移动小车自身的半径和环境地图中自由空间的距离信息,搜索出的路径通常接近障碍物,如图2虚线所示。即使搜索产生的路径在自由空间中,当移动小车接近障碍物时,也很容易发生碰撞。为了降低这种风险,需要一条远离障碍物的路径。传统方法是通过将障碍物膨胀到比移动小车大得多的半径来解决的。但是,这种过度膨胀策略并不适合在障碍物杂乱的室内环境中进行路径规划。

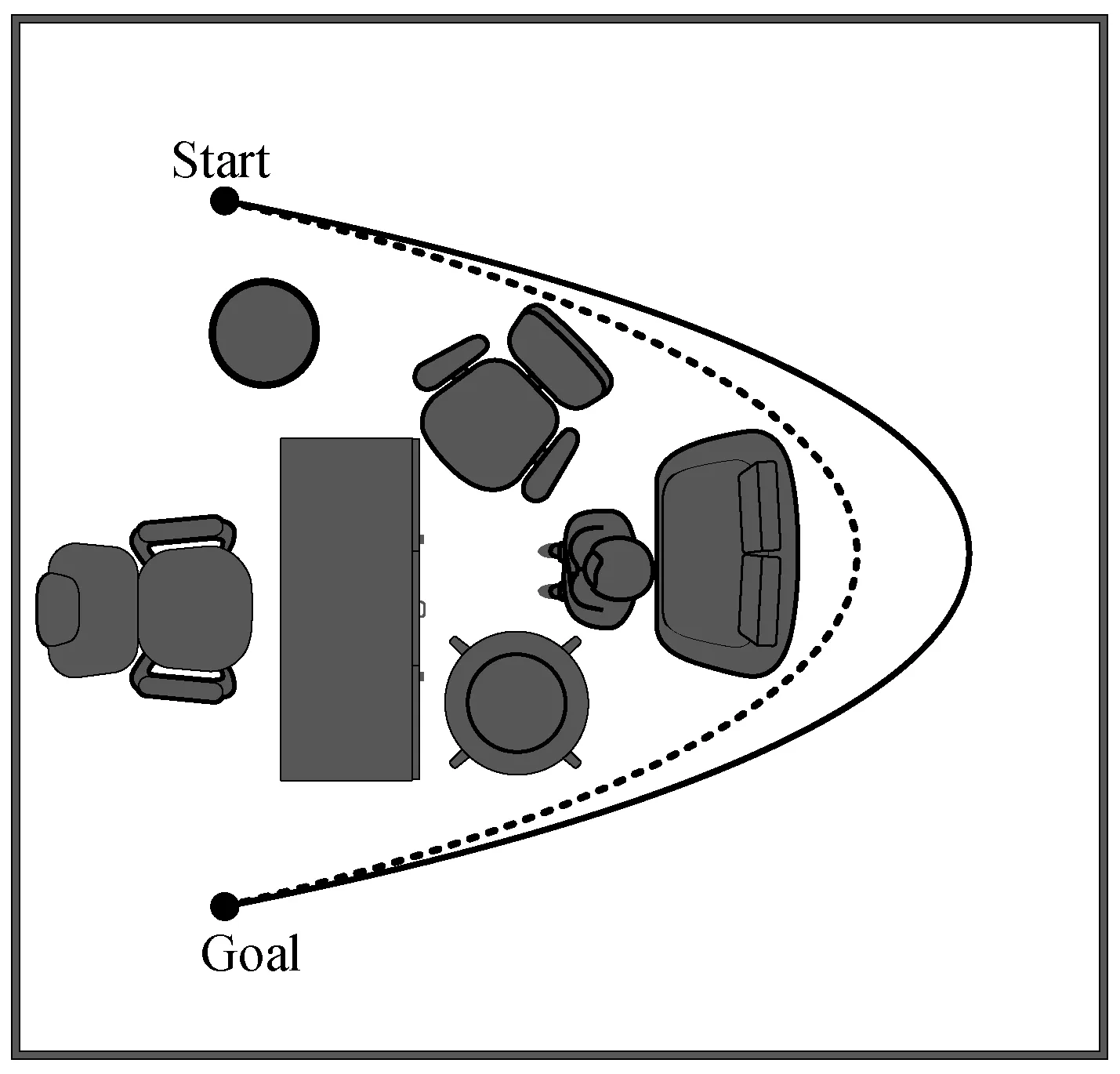
图2 前端搜索路径和后端优化路径

本节提出基于三次均匀B样条的软优化算法优化路径。根据移动小车行进过程中,安全性能是首要因素进行如下改进：由于改变均匀B样条曲线的局部控制点,则相应控制点的分段曲线也会改变,根据均匀B样条曲线恒位于其凸包之内的性质,通过引入软约束总成本函数,分别对控制点间的平滑度、控制点和障碍物的安全距离信息、移动路径上速度和加速度的限制,优化移动路径上的控制点的位置。优化后的移动小车路径和障碍物保持安全距离,并且优化之后的路径更加平滑。下面进行详细说明。

2.1 均匀B样条曲线

均匀B样条曲线是由控制点{Q0,Q1,…,QN}、次数pb和节点向量[t0,t1,…,tM]组成的分段多项式。其中：{Q0,Q1,…,QN}⊂R2,{t0,t1,…,tM}⊂R。控制节点数、次数和节点向量数满足式(13)。

M=N+pb+1

(13)

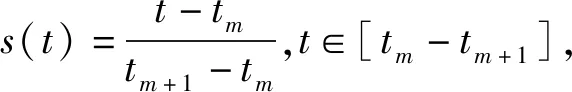
[Bi-pb,pb+1(s(t))Bi-pb+1,pb+1(s(t)) …Bi,pb+1(s(t))]=[1s(t)s2(t) …spb(t)]Mpb+1

(14)

式中：Mpb+1是由次数确定的常数矩阵[15]。本文设置均匀B样条曲线的次数pb=3,常数矩阵M4如式(15)所示。

(15)

则路径P(s(t))如式(16)所示。

(16)

2.2 凸包性质

三次均匀B样条曲线是被每段控制点组成的多边形包围,如图3所示。均匀B样条曲线的导数仍然是均匀B样条曲线。

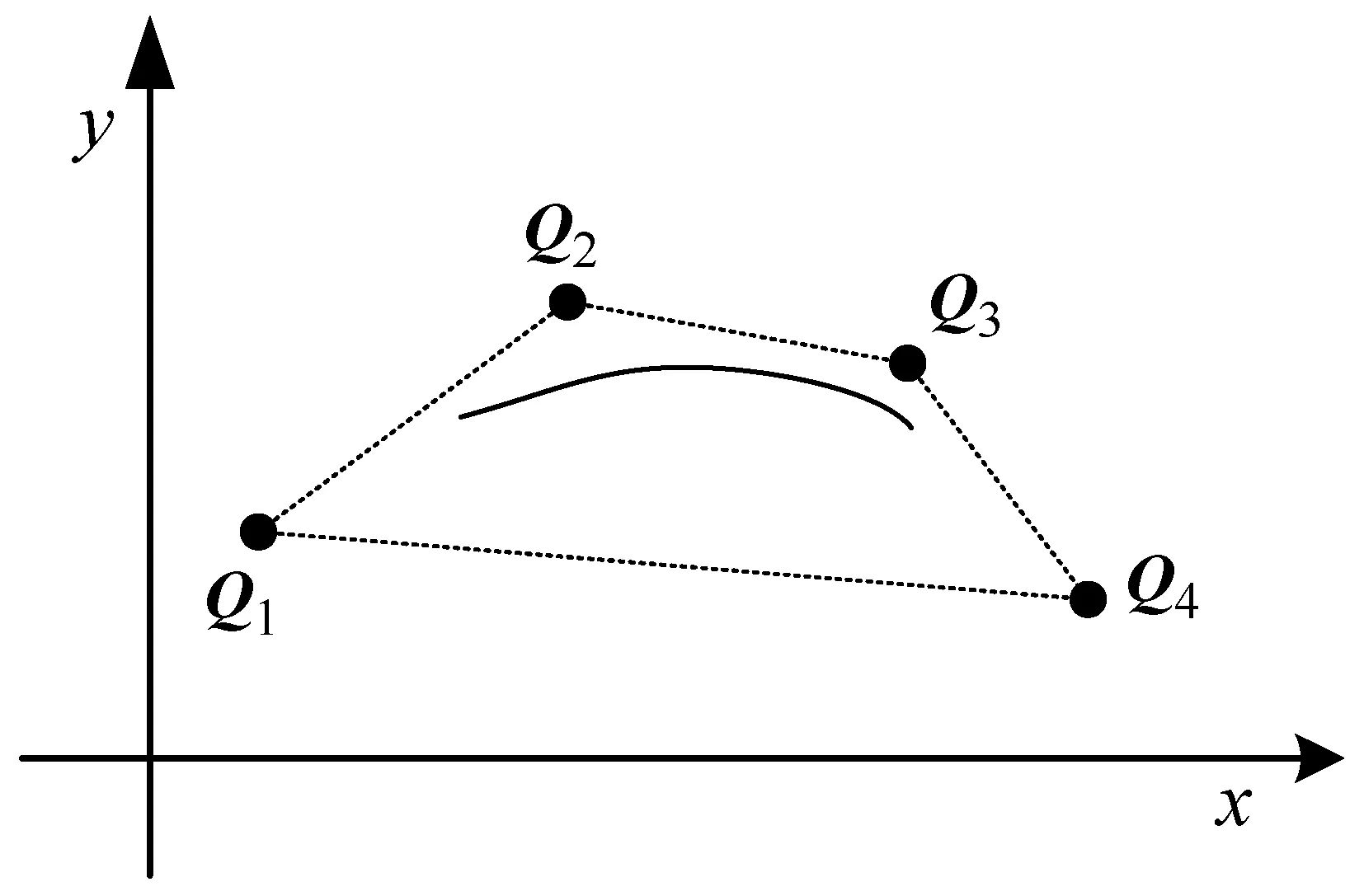
图3 三次均匀B样条曲线

对于运动可行性,只需约束所有速度控制点{V0,V1,…,VN-1}和加速度控制点{A0,A1,…,AN-1},使得Vi∈[-vmax,vmax]2和Ai∈[-amax,amax]2,其中Vi和Ai如式(17)所示。

(17)

安全性是移动小车行进过程中非常重要的因素。在移动小车行进过程中,不仅需要满足移动路径的无障碍物碰撞,而且还要保证移动小车远离障碍物。

根据均匀B样条曲线的凸包性质,则凸包内的路径也是无障碍碰撞的。如图4所示,保证dp>0,其中dp是凸包中的任意一个路径点到栅格障碍物的距离,通过三角不等式,使得dp≥dc-rp,其中：dc是控制点到栅格障碍物的距离;rp是控制点到任意一个路径点的距离。因为P在凸包内,得到控制点到路径点的距离rp≤r12+r23+r34,其中r12、r23、r34是相邻控制点的距离,因此dp>dc-(r12+r23+r34)。为了保证凸包的安全性,只需满足式(18)。

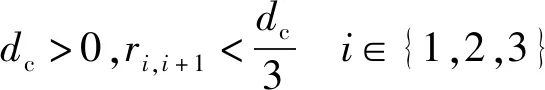
(18)

2.3 软约束方法

三次均匀B样条曲线在本质上是连续的,不需要显式地强制连续性,软约束方法[16-17]利用距离信息将路径推离到距离障碍物较安区的地方,提高了计算效率和收敛速度。由N+1个控制点{Q0,Q1,…,QN}定义的三次均匀B样条路径,本节只需要优化N-5个控制点{Q3,Q4,…,QN-3},前三个和后三个控制点分别对应当前状态和目标状态不需要更改,软约束总成本函数ftotal[18]如式(19)所示。

ftotal=λ1fs+λ2fc+λ3(fv+fa)

(19)

式中：fs是平滑度成本;fc是碰撞成本;fv、fa分别是速度和加速度的限制成本;λ1、λ2和λ3分别是平滑性、安全性、运动可行性的权重值。

本节通过控制点的几何信息并且不依赖时间信息的函数fs来定义平滑度成本如式(20)所示。

(20)

式中：控制点Q1、Q2、QN-2、QN-1是不需要进行优化,但是需要计算总体的平滑度。从物理层面看,式(20)中Qi+1-Qi和Qi-1-Qi分别是连接节点Qi+1、Qi和节点Qi-1、Qi的两个弹簧的结合力。如果所有项都等于零,则所有的控制点都将均匀分布在一条直线上,这是理想状态的平滑。

本节通过作用于控制点的障碍物的排斥力来定义碰撞成本fc,如式(21)所示。

(21)

式中：d(Qi)表示控制点Qi和障碍物之间的距离;Fc是可微分的函数。通过设置指定障碍物距离的阈值dthr来计算惩罚值,如式(22)所示。

(22)

因为碰撞成本函数将控制点推离障碍物,所以式(18)中dc>0显而易见,此外,ri,i+1仅依赖均匀B样条曲线的参数,根据大量实验证明,只需要设置ri,i+1<0.2,路径在大多数情况下符合安全性要求,但是在极端情况下可能是无效的,例如,室内环境非常混乱。即使这样,也能通过重新设置均匀B样条曲线参数,选择较小的ri,i+1,仍然满足式(18)。

本节通过惩罚路径上的速度和加速度超过阈值vmax、amax来定义惩罚项,速度和加速度的惩罚项如式(23)所示。

(23)

由均匀B样条曲线的凸包性质,得到不可行速度和加速度控制点的限制成本如式(24)所示。

(24)

3 仿真实验

本节针对提出的基于均匀B样条曲线的移动小车路径规划方法的实验结果分析和说明。实验平台配备TITAN Xp GPU,Intel Xeon(R) E5-26900 CPU,2.9 GHz×32,64 GB内存,机器人操作系统(Robot Operating System,ROS),Ubuntu16.04操作系统。本文提出的路径规划方法在C++11环境下通过非线性优化解算器NLopt[19]实现。在仿真实验中,路径搜索时间间隔τ=0.5,移动小车半径r=0.1 m,优化设置λ1=10,λ2=1,λ3=0.1,本节提供室内三维环境地图数据来验证基于均匀B样条曲线的移动小车路径规划方法的性能。

3.1 实施细节

当一定移动小车在未知室内环境中运动时,由于传感范围有限,它不得不频繁地重新规划自己的路径。为了提高效率,我们采用了循环时间规划方案,其中路径只在已知空间内生成。一旦路径在该范围之外结束,前端路径搜索就终止,随后是后端路径优化。在未知的空间进行规划往往是徒劳的,因此可以提升路径搜索的速度。

重新规划路径机制在两种情况下触发。首先,如果当前路径与新出现的障碍物发生碰撞,就会触发重新规划路径机制。这确保了一旦检测到任何碰撞,就有新的安全路径可用。其次,在固定的时间间隔调用重新规划路径机制,使得最新的环境信息能够融入到路径搜索中。

3.2 实施结果分析

为了验证基于均匀B样条曲线的移动小车路径规划方法的安全性能,进行仿真实验。本节将初始搜索路径和三次均匀B样条曲线优化后的路径进行安全性能对比。选取了室内三维环境地图进行验证,如图5所示。图6为初始搜索路径和初始搜索路径障碍物距离曲线,可以看出,初始搜索路径存在路径尖峰拐点,并且移动小车质心和障碍物的最短距离最小值约为0.138 m,考虑到移动小车自身半径为0.1 m,在移动小车行进过程中不符合安全性能的需求。

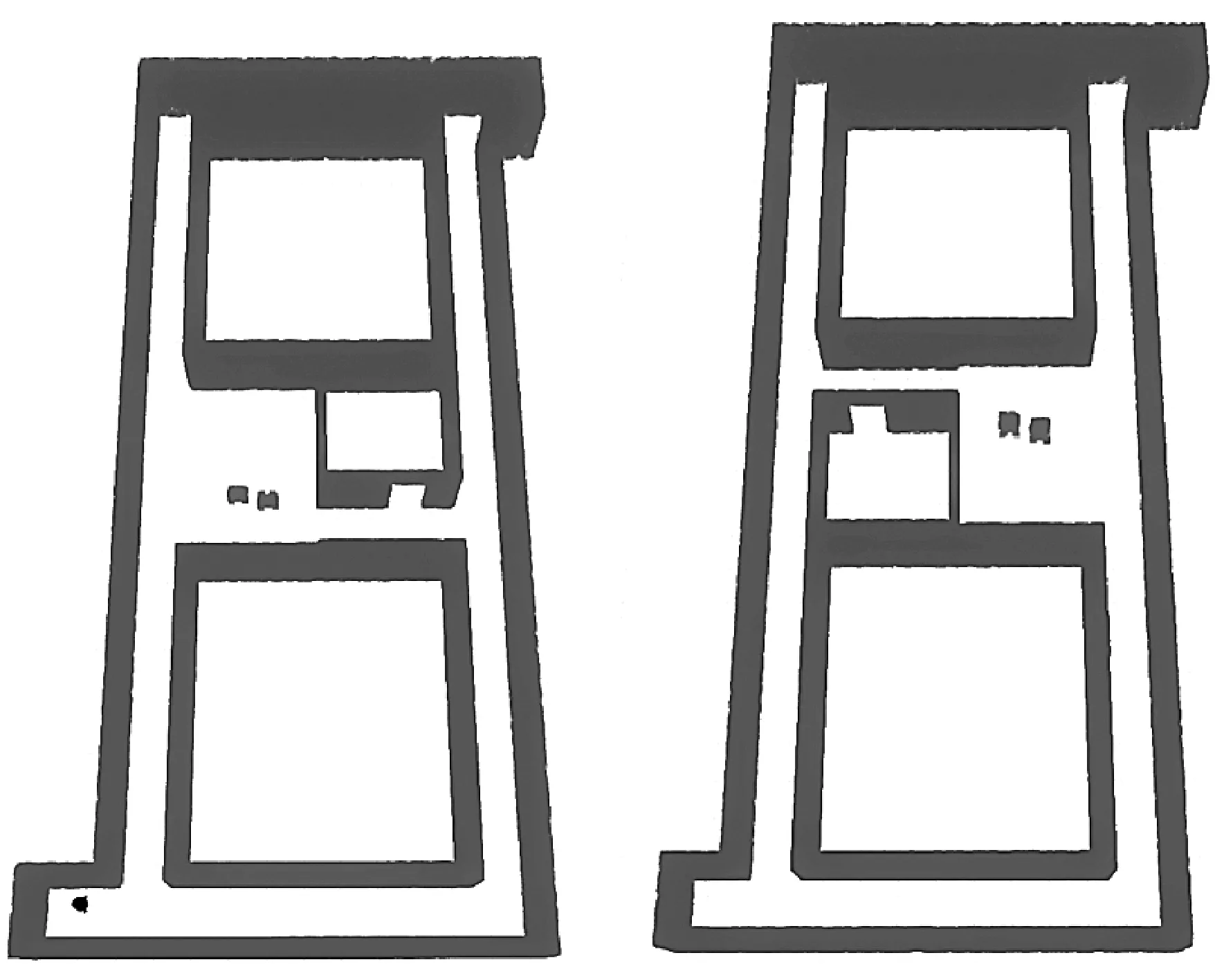
图5 室内三维环境地图

安全性对于路径规划是非常重要的因素。图7为三次均匀B样条曲线优化后的路径和路径障碍物距离曲线,可以看出,优化后的路径消除了路径尖峰拐点,并且移动小车质心和障碍物的最短距离最小值约为0.303 m,优化了移动小车转向时靠近障碍物的路径,优化后的路径满足移动小车行进过程中安全性能的需求。

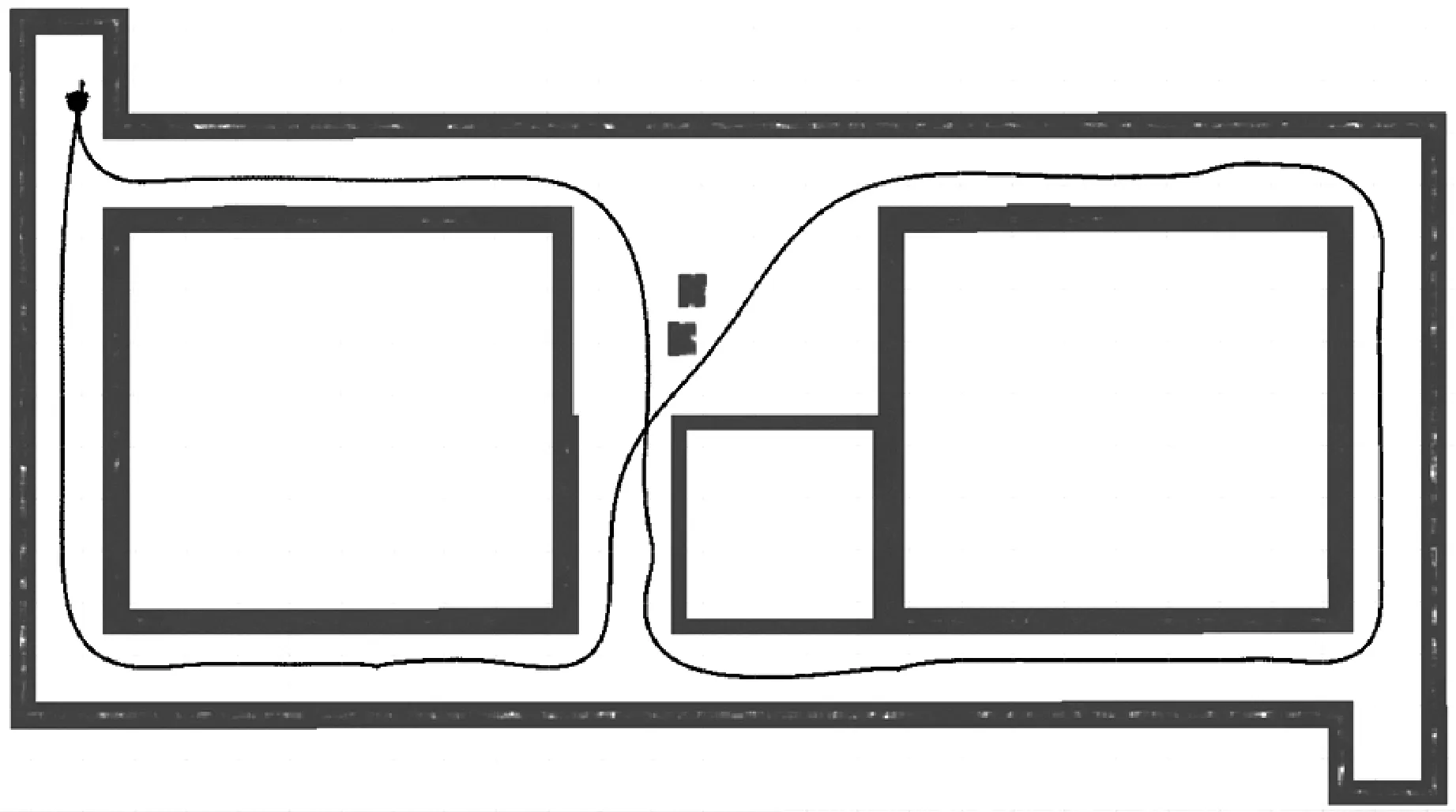
(a) 路径

最后,选取简单室内环境仿真地图,将扩大搜索邻域A*算法和本文算法相比较,设定移动小车起点坐标为(5,-5),两段终点目标分别是(-4,7)和(-5,-7)。图8为两种路径规划算法效果。选择路径长度、搜索时间和采样节点数作为评价指标,记录30次实验的平均值如表1所示。本文算法搜索时间更短、搜索速度更快,在确保路径安全性的前提下,路径变长。

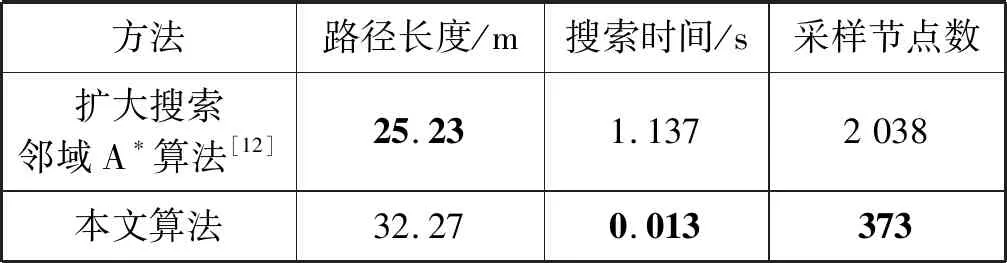
表1 仿真实验对比分析

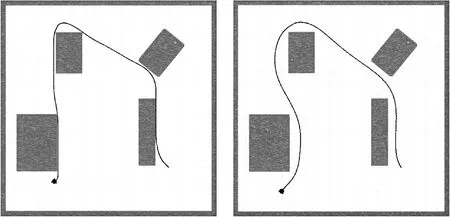
(a) 扩大搜索邻域A*算法 (b) 本文算法图8 两种算法路径规划效果比较

4 结 语

路径规划是移动机器人研究领域的一个重要研究方向。移动小车行进过程中,安全性是首要考虑因素,本文针对安全性提出一种基于均匀B样条曲线的移动小车路径规划方法。前端采用运动路径搜索方法,寻找一条初始路径,后端结合距离信息和均匀B样条曲线优化方法进一步提高路径的安全性和平滑性。利用均匀B样条曲线的凸包性质,与扩大搜索邻域A*算法相比,显著提高了移动路径的安全性和实时性。

从仿真实验来看,基于均匀B样条曲线的路径能够在室内环境下进行仿真验证。在未来的工作中,主要针对大规模或动态环境等极端情况下,验证移动小车路径的安全性。