基于梯次启动与优化算法的多集群风机最优调频方法

陈汝斯,李大虎,周泓宇,周悦,饶渝泽,姚伟

(1. 国网湖北省电力有限公司电力科学研究院,武汉市 430077;2. 国网湖北省电力有限公司,武汉市430077;3. 强电磁工程与新技术国家重点实验室(华中科技大学),武汉市 430074)

0 引 言

随着工业的迅猛发展,化石能源被不断开采利用,其全球储量逐年下降[1],面临逐渐枯竭的危机[2]。可再生能源因其可持续发展[3]和低污染[4]的特点,被认为是解决能源短缺和环境恶化的有效途径[5]。其中,风力发电因其技术相对成熟和市场化程度高等优势[6],已普遍应用于传统发电不足领域[7]。

风力发电机(wind turbines, WT)通过直流(direct current, DC)输电并网是一种主要的风电消纳方式[8],然而WT的转子速度可能会与系统频率解耦,难以为电网提供有效的惯性支撑,严重威胁电力系统的安全稳定运行[9]。其中,双馈异步发电机(doubly-fed induction generator, DFIG)具有运行速度范围广、体积小、成本低等优点,已经成为当前应用最广泛的风力发电机。但与传统的同步发电机(synchronous generators, SG)相比[10],DFIG无法及时对系统频率扰动做出响应。此外,如果风电并网带来的额外有功功率备用容量仅由传统机组提供,那么系统运行成本将大大增加,且造成能源浪费。综上所述,研究大规模风电并网的频率特性和频率调节控制具有重要意义[11]。

近年来,风电场(wind farms, WF)开发了多种频率调节控制策略,主要分为储能控制、卸荷控制、转子转速控制和下垂控制等[12]。特别是,文献[13]和[14]通过释放储能设备的能量实现了交流(alternative current, AC)侧的频率调节,然而,加入储能设备会提高成本。文献[15]采用了卸荷控制来实现一次频率调节,这种控制方法保留了备用电源,但严重阻碍了风能的有效利用。文献[16]运用转子转速控制策略提供系统频率支撑。文献[17]提出在外环控制基础上引入有功功率-频率下垂特性以实现频率调节。特别地,下垂控制能够解决柔性DC系统功率和AC电网频率之间的耦合问题,但其逆变器仍不能提供惯性支撑,不能实现一次频率调节,也不能抑制如SG容量不足造成的负荷干扰。鉴于下垂控制中存在的主要问题,虚拟同步发电机技术应运而生[18]。文献[19]将虚拟调速器引入惯性控制环节,以提供惯性响应并实现一次调频。

风电场参与频率支撑控制策略主要可以分为:转子动能控制、功率备用控制[9]。采用转子动能控制时,为了最大化利用捕获的风能,风电场各风机正常工作时,均采用最大功率点跟踪方式。在该方式下,风电机组可通过附加控制响应频率变化参与系统频率调节,包括惯性控制和下垂控制。采用转子动能控制,风机通过释放转子动能参与频率调节,无需弃风保留备用功率。由于释放转子动能提供调频功率,该控制的时间尺度远快于桨距角控制的时间尺度[20],因此可以认为采用转子动能控制时,风机桨距角保持不变。尽管采用转子转速控制能够使工作在最大功率跟踪方式下的风电机组提供一定的频率支撑功率,但由于缺少功率备用,支撑时间和容量有限[21]。因此,可采用减载控制的方法,使风电机组具有和同步发电机类似的调频备用功率。功率备用控制具体可以分为超速减载备用和变桨减载备用两类:超速减载是将风电机组工作点从最大功率跟踪点右移,使风机工作在减载工作点处,此时风机转速相较于最大功率点跟踪时增大,而风机的输出功率因部分功率备用而小于最大功率;变桨控制则是通过改变风机桨距角实现功率备用。

然而,上述研究仅考虑对电力系统的一次频率下降(first frequency drop, FFD)进行抑制。事实上,在风机转速恢复过程中,二次频率下降(second frequency drop, SFD)也是不可避免的,且当有功功率严重不足时,它比FFD更为严重。因此,文献[22]开发了一种基于海上WF的两级组合控制策略,以提供适当的频率支撑并缓解SFD。然而,上述策略的控制器关键参数是通过试错法确定的,难以保证控制精度和稳定性,且耗费时间多。

为解决二次频率跌落、控制参数选取困难等问题,本文开发了一种基于蒲公英优化(dandelion optimizer, DO)[23]算法的参数优化策略,对梯次启动自适应惯性下垂控制器的参数进行优化,以降低FFD、SFD甚至三次频率下降(third frequency drop, TFD)。DO算法是一种新提出的启发式算法,文献[23]从准确性、稳定性、收敛性、可扩展性等方面证明了DO相较于已有的启发式算法具有更优异的性能。此外,本文的主要贡献可归纳为以下两点:

1)运用梯次启动策略调整控制WF,即每个WF被分为集群1和集群2,分别在负荷变化和转子角速度恢复时进行频率调节,在保证对一次频率下降支撑效果的同时,有效缓解二次频率跌落。

2)采用自适应惯性下垂控制方案,基于DO优化算法调整所设计控制器的8个未知参数,建立柔性直流系统功率与电网频率之间的关系,显著增强系统惯性,提升频率支撑能力。

1 建模与控制方案

1.1 风力涡轮机建模

根据空气动力学原理[24],风轮的功率可以表示为:

(1)

式中:ρ、S以及v分别代表空气密度、WT叶片扫过的面积、风速;R为WT叶片的半径。

WT的输出机械功率为:

(2)

式中:λ和θ分别为叶尖速比和WT的桨距角;ω为WT的转子角速度,rad/s;Cp(λ,θ)为风能利用系数,具体表达式详见文献[25]。需要指出的是,本文仅考虑风电机组参与系统惯性和一次调频过程,时间尺度为10 s左右,因此在这一暂态过程中,可认为风速不变,风机出力大小不变。

由文献[25]可知,WT的风能利用系数Cp由λ和θ决定,其关系如图1所示。由图1可以看出,在一定的桨距角下,随着叶尖速比的增大,风能利用系数先增大后减小。最大风能利用系数随桨距角的增大而减小。因此,通过控制WT在不同风速下的桨距角,可以获得最大的功率输出。此外,为了获取最大功率输出,WT的桨距角θ保持为0°,本文将额定风速设定为12 m/s。

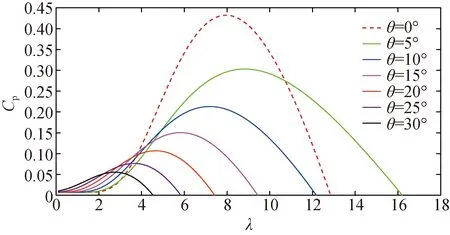
图1 不同桨距角下风能利用系数与叶尖速比的关系

当风机参数固定后,对于特定的一台风机,当风速一定时(即风轮面功率一定时),其风能利用系数与其风机转速相关(风机输入机械功率=风轮面功率×风能利用系数)。不同风速下,风机的最大输出功率均满足:Pe=koptωr3,其中kopt是与风力机叶片面积、风轮半径、空气密度等相关的常数,ωr为转子转速。

1.2 梯次启动自适应惯性下垂控制方案

如图2所示,测试系统采用了基于WF和AC系统的三区四端多端高压直流测试系统(VSC-multi-terminal high voltage direct current system, VSC-MT-HVDCS),该系统包括两个WF、一个VSC-MT-HVDCS和一个AC系统[26]。其中,每个WF包括5个等效WT,它们一起向AC系统传输电能。在本文中,WF1中WT1—WT5的转子角速度依次确定为0.90 pu, 0.95 pu, 0.85 pu, 1.00 pu, 1.05 pu。此外,WT6—WT10的转子角速度也依次确定为0.90 pu, 0.95 pu, 0.85 pu, 1.00 pu, 1.05 pu。注意,只有WF1的WT在频率事件发生,即负荷增加后,才通过梯次启动自适应惯性下垂控制方案参与频率支撑,而WF2的所有WT均在最大功率点(maximum power point, MPP)状态下运行。同时,WF1中的WT根据其转子角速度按一定比例分类为不同的集群。例如,在负荷增加时,WT2、WT4和WT5属于集群1,而若集群分类比为3∶2,则集群2涉及WT1和WT3。相反,在负荷减少时,WT1—WT3被分类为集群1,若分类比也是3∶2,则WT4和WT5被分类为集群2。需要指出的是,由于多端柔性直流的解耦作用,在考虑频率信号在多个交流系统之间传递时,本文直接采用特定通信线路进行频率传递,延时主要包括了信号在发送端的调制延时,信号传输延时,信号在接收端的解调制延时。由于在光纤通信中,信号传输速度接近光速,信号传输延时较低,但是信号调制和解调延时较长。因此,在仿真中考虑了200 ms的信号传递延时。

当风机稳定运行在MPPT模式下时,风机输入的机械功率已经是该风速下对应的最大值,因此当事故发生时,风机只能通过附加控制(包括模仿常规同步机的惯性控制和下垂控制)释放转子动能,向上调频时降低转速,暂时性(风机转速具有安全限值)对系统提供频率支撑的电磁能。

风机的转子运动方程如下所示:

(3)

式中:Pm为输入风机机械功率;ΔP(t)表示风机频率支撑控制中的附加功率值,包含下垂控制部分和惯性控制部分;Tw表示风机转动惯量。

对式(3)两侧积分可得:

(4)

式中:ωr0代表风机调频前的初始转速。

风机转子动能如下:

(5)

由式(4)、(5)可知,风机提供频率支撑的本质是牺牲风机的转子动能换取输入系统的电磁能。综上,风电机组参与系统向上频率调节时,将退出MPPT模式,风机转速下降释放转子动能,从而输出功率增加,提供频率支撑功率。

WT的有功功率参考值Pref,i主要由三部分组成,即该WT实时转子角速度ωi下的最大功率点(maximum power point,MPP)、惯性控制和下垂控制,如图3所示。将频率下垂控制和虚拟惯性控制附加在风电机组的最大功率跟踪控制环节上,风电机组在交流系统发生负荷扰动期间能够通过释放转子动能增发功率,提供主动频率支撑。风机功率转速曲线如图4所示,当事故未发生时,其工作点在PMPPT处。当故障发生后,风机转速下降释放转子动能ΔE,风机输出电磁功率增加,提供频率支撑功率。此时,风机功率将暂时高于MPPT的功率值,其工作点由PMPPT转移到Pop1。由于风机在以上频率支撑过程中通过暂时释放转子动能换取输入系统的电磁能,其转速下降,而风机具有安全转速范围,因此风机在该阶段后需要进行转速恢复。转速恢复的过程可以通过风机工作点由Pop1到Pop2简单描述,与上一阶段相反,该阶段需降低输出电磁功率重新恢复转子动能,该阶段对系统产生的功率缺额需通过适当的转速恢复策略减缓,否则将引起二次频率跌落问题。

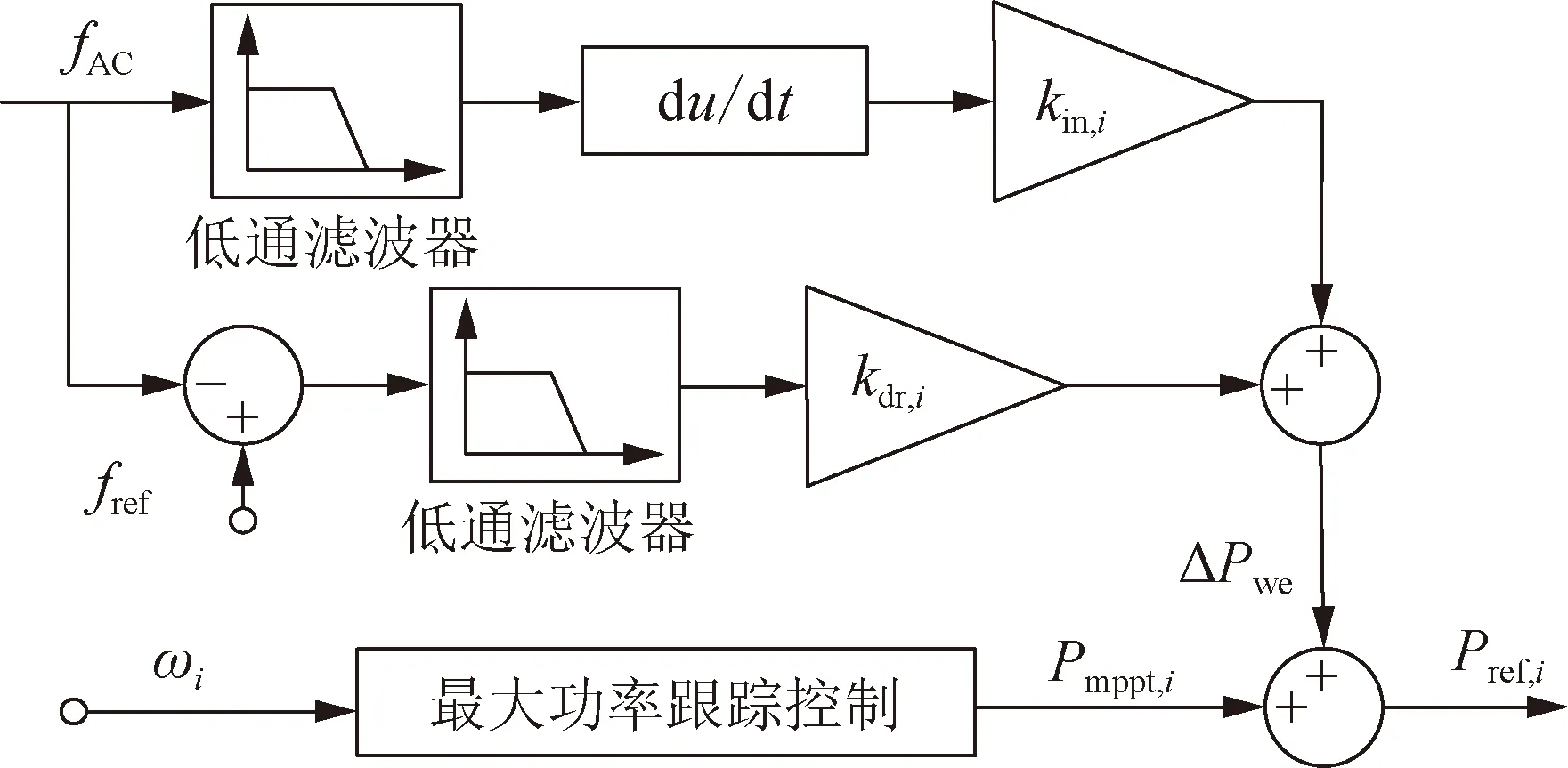
图3 风电机组综合惯性控制

图4 风电机组功率-转速曲线

对于第i个WT,梯次启动自适应惯性下垂控制方案如图5所示。WT经过一定延时Δt后与另一集群的WT进行匹配。也就是说,利用集群1和集群2分别按一定的顺序支撑系统频率。同时,惯性控制系数和下垂控制系数均随ωi自适应变化,具体可描述为:

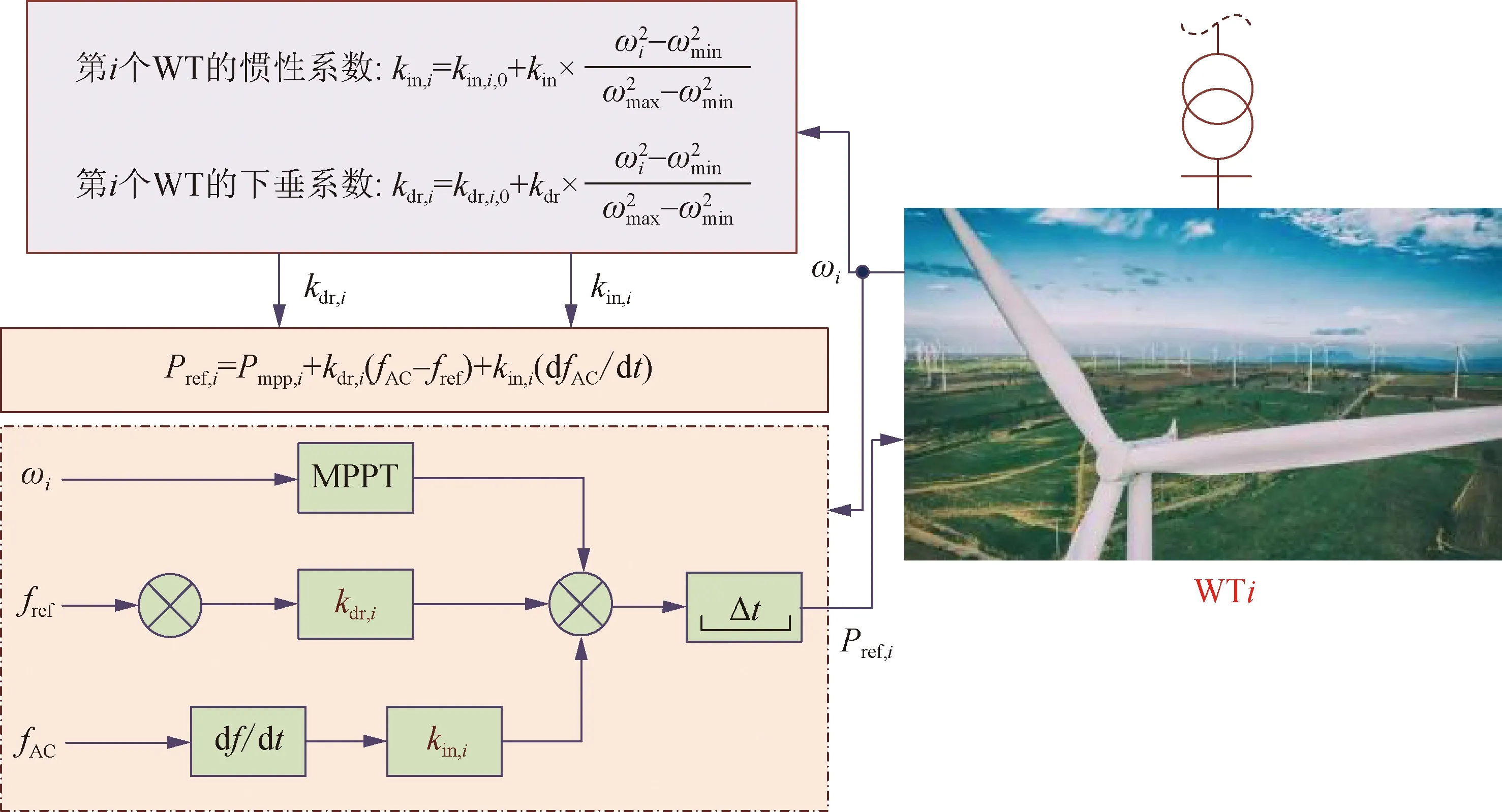
图5 第i个WT的梯次启动自适应惯性下垂控制方案

(6)

(7)

式中:kin,i,0为惯性控制系数初始值;kdr,i,0为下垂控制系数初始值;ωi为第i个WT的转子角速度;ωmin和ωmax分别为WT的最小和最大转子角速度;kin为惯性系数;kdr为下垂系数。由于ωmin和ωmax的限制风机的惯性下垂系数并不会无限制地增大。以风机释放转子动能参与调频为例,在这一过程中,风机转子转速ωi减小,逐渐逼近安全范围最低值ωmin,此时风机的自适应惯性下垂系数kin,i和kdr,i将逐渐减小逼近kin,i,0和kdr,i,0。因此,只要设计合理的初始值kin,i,0和kdr,i,0,就可以保证在参数自适应变化过程中,风机惯性下垂系数kin,i和kdr,i始终保持在合理范围内。

WT的输出功率参考值为:

(8)

式中:fAC为AC系统频率;fref为系统频率参考值;Pmpp,i为WT的MPPT参考值。本文在VSC1中进行测试,设定fref=50 Hz,ωmin=0.70 pu,ωmax=1.20 pu[6]。

与采用常系数的传统下垂控制方法相比,自适应惯性下垂控制系数随WT的实时转子角速度ωi变化,不仅能保证转子在安全条件下运行,而且能提高风能的利用效率,更能及时调整WT的状态。此外,AC系统频率fAC的变化率被用作惯性控制的输入信号。频率响应初级阶段的频率偏差较小,频率变化率较大,自适应惯性控制可快速提供频率支撑[27]。采用下垂控制来模拟SG的一次调频,能够实现频率事件后期的稳态频率改善。

值得注意的是,可以从文献[22]中获得关于整个系统的建模参数和VSC站控制策略的更多信息。

2 基于DO的梯次启动自适应惯性下垂控制器的参数设计

2.1 DO的数学描述

受蒲公英依靠风传播种子的启发,文献[18]提出了一种新颖的DO算法,该算法充分考虑风速以及天气对蒲公英种子传播的影响,可概括为三个阶段,上升阶段、下降阶段以及着陆阶段。

为了更高效地实现种群进化,将种群初始化为:

(9)

式中:p表示种群规模;D为变量维度,每个候选解都在给定上界(BU)和下界(BL)之间随机生成,第i个个体Xi描述为:

Xi=rand×(BU-BL)+BL

(10)

式中:rand为[0,1]间的随机数,BU和BL如下所示:

BL=[bl1,…,blD]

BU=[bu1,…,buD]

(11)

式中:bli、bui(i=1,…,D)分别为上下边界候选解。

此外,将适应度值最优的个体选为初始精英,即蒲公英种子最适合生长的位置。初始精英个体Xelite(以最小值为例)可表示为:

(12)

式中:X{·}代表初始精英个体值;find代表具有相等值的两个索引;f(Xi)代表第i个个体的函数。

在上升阶段,受到风速、空气湿度等天气因素影响,蒲公英种子将会上升至不同高度。特别地,天气可以分为晴朗和阴雨两种情况。

在晴朗情况下,风速可以被认为具有对数正态分布lnY～N(μ,σ2)规律。在此基础上,随机数沿Y-轴分布更为均匀,蒲公英种子能够被随机吹到更远的地方。与此同时,蒲公英种子上方旋涡受风速影响被不断调整,使蒲公英呈螺旋状上升,可以表示为:

Xt+1=Xt+α×vx×vy×lnY×(Xs-Xt)

(13)

式中:Xt为第t次迭代时蒲公英种子的位置;α、vx、vy分别为自适应参数、上升方向系数、下降方向系数;Xs表示迭代期间搜索空间随机选择的位置,其数学表达式为:

Xs=rand(1,D)×(BU-BL)+BL

(14)

式中:rand(1,D)为1行D列的随机矩阵。

此外,lnY服从μ=0和σ2=1的对数正态分布,可以描述为:

(15)

式中:y表示标准正态分布N(0,1)。

自适应参数α用以调整搜索步长,可表示为:

(16)

式中:T为调整系数;tt为搜索时间。

蒲公英因分离旋涡作用而产生的升力系数可表示为:

(17)

式中:γ为-π和π之间的随机数。

在阴雨情况下,受限于空气阻力、湿度等天气因素,蒲公英种子无法随风适当上升。因此,蒲公英种子将在局部领域进行搜索,可以描述为:

Xt+1=Xt×k

(18)

式中:k用于调节蒲公英种子的局部搜索区域,并利用式(19)计算该区域,表示为:

k=1-rand×q

(19)

(20)

综上所述,蒲公英上升阶段的数学表达式为:

(21)

式中:rand()为不限制范围的随机数。

在下降阶段,以布朗运动模拟蒲公英种子的运动轨迹,可以描述为:

Xt+1=Xt-α×βt×(Xmean_t-α×βt×Xt)

(22)

式中:βt表示布朗运动,是标准正态分布的随机数;Xmean_t为种群在第t次迭代的平均位置,其数学公式为:

(23)

在着陆阶段,算法有望收敛到全局最优解,得到的最优解是蒲公英种子最容易存活的近似位置,可以表述为:

Xt+1=Xelite+flevy(ε)×α×(Xelite-Xt×δ)

(24)

式中:Xelite表示蒲公英种子在第t次迭代的最佳位置;δ为代表[0,2]间的线性递增函数;flevy(ε)为飞行函数,可表示为:

(25)

式中:β代表介于0和2间的任意数;s是固定常数,取0.01,w和tr是[0,1]间的随机数。此外,σ的数学表达式为:

(26)

δ计算表达式为:

(27)

2.2 基于DO的控制器参数优化

为了获得最佳的频率调节性能,本节提出基于DO的梯次启动自适应惯性下垂控制器的参数优化策略。一方面,本文主要关注图6所示负荷增加后系统频率fAC的动态响应特性,即FFD、SFD和TFD。其中,fFFD,fSFD和fTFD分别表示FFD、SFD和TFD的最低点。具体而言,在t0处发生频率事件后(即对于集群1的WT,Δt等于0),集群1立即投入运行,而当集群1的转子角速度在tⅠ处开始恢复时(即对于集群2的WT,Δt为0),则启动集群2,风机梯次启动示意图如图7所示。

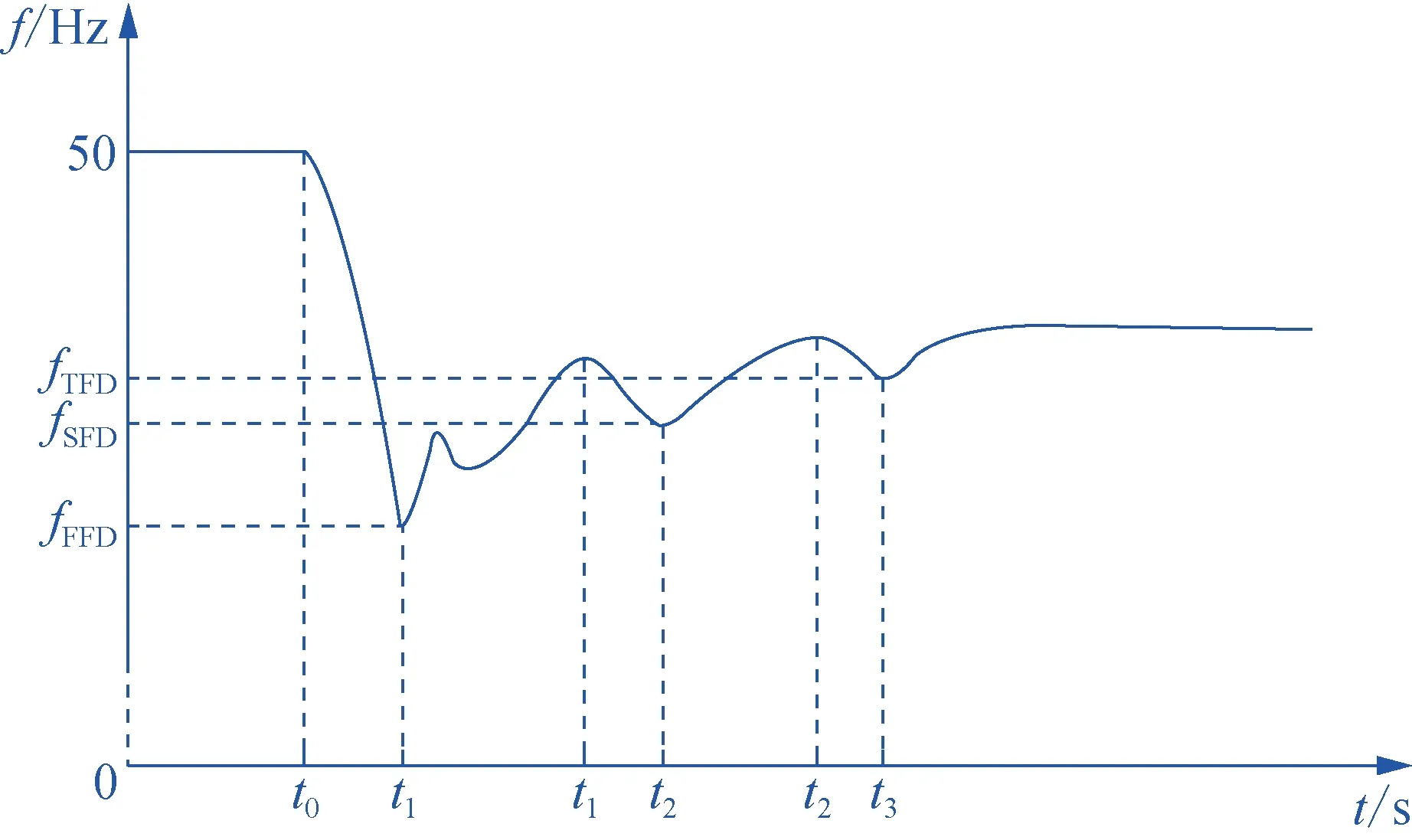
图6 负荷增加时系统频率的一般动态特性

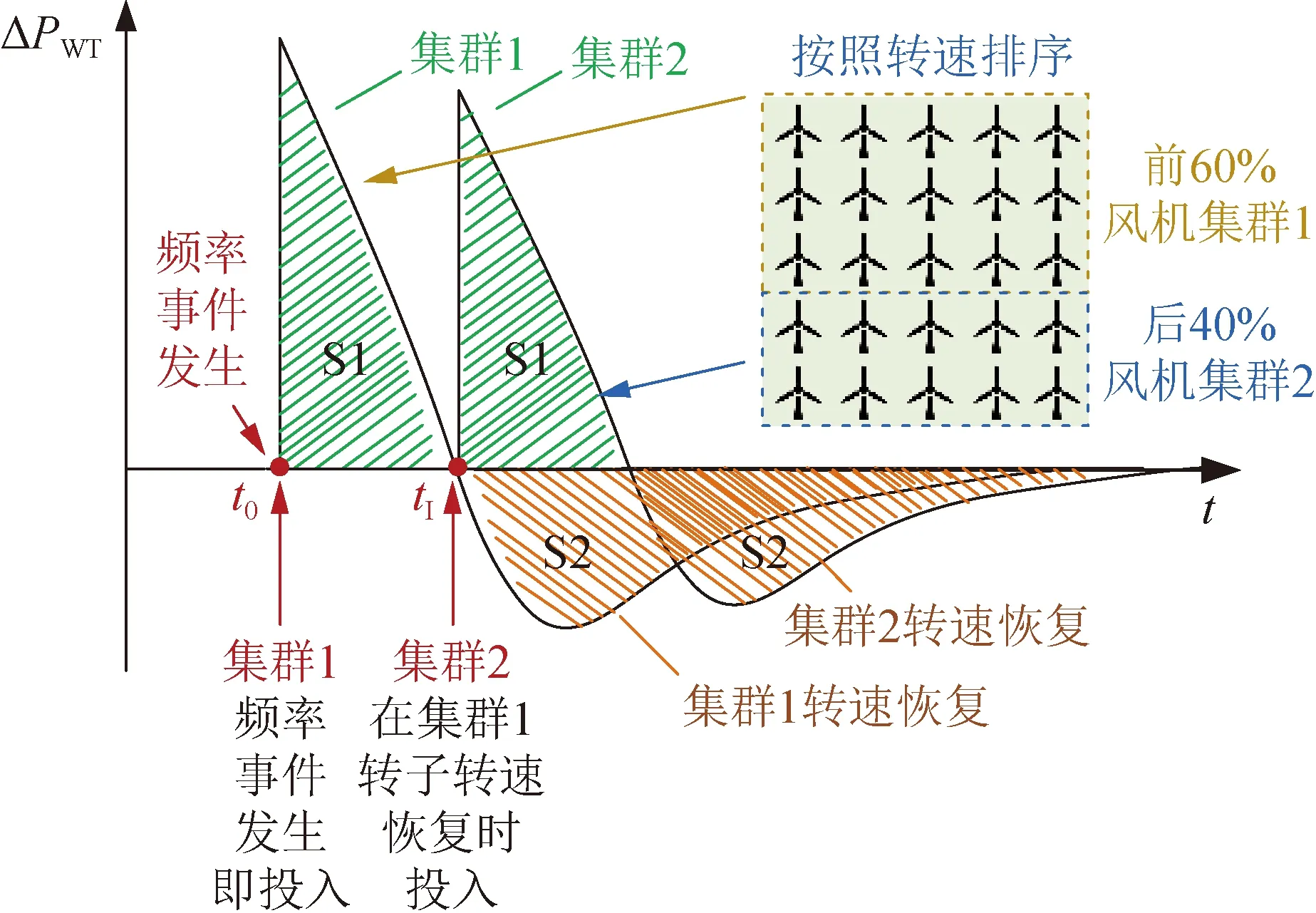
图7 风电机组梯次启动示意图

另一方面,还考虑了频率偏差SIoFD和频率变化率的积分SIoFVR,这两者主要体现了系统频率波动的全局信息。其中SIoFD和SIoFVR可以表示为:

(28)

(29)

如式(30)所示,根据相对重要性为每个指标分配一个系数,并将它们相加作为适应度函数。

Ffit=(SIoFD,SIoFVR,fFFD,fSFD,fTFD)=min{AIoFD+AIoFVR+(200fFFD+100fSFD+100fTFD)·50}

(30)

表1 优化参数的范围

基于DO的梯次启动自适应惯性下垂控制器参数优化伪代码如表2所示。

表2 基于DO算法的控制器参数优化伪码

3 算例研究

本节中,在负荷增加50、100以及150 MW三种情况下,基于DO对梯次启动自适应惯性下垂控制器的参数进行优化,以验证和评估优化参数的有效性。所有案例研究均在MATLAB/Simulink环境下进行,带可变步长解算器。此外,种群规模p和最大迭代次数Tmax分别设置为30和200。注意,所有负荷变化均发生在第5 s。同时,集群1和集群2分别在负荷变化和转子角速度恢复时参与频率调节,即Δt=0 s和Δt=5 s。

表3—5分别给出了在负荷增加50、100和150 MW时,无WF参与调频、试错法和DO算法得到的最优控制参数。

表3 负荷增加50 MW情况下不同方法获得的最佳控制参数

表4 负荷增加100 MW情况下不同方法获得的最佳控制参数

为了验证基于DO参数优化的控制器在负荷增加时的性能,在第5 s时系统负荷分别增加50、100和150 MW。该频率事件中,集群1(即WT2、WT4和WT5)在第5 s立即启动,集群2(即WT1和WT3)在第10 s启动。表6为不同方法获得的FFD、SFD和TFD。图8详细描述了在多种负荷增加下系统的动态频率响应。从图8可以看出,与无WF参与和试错法相比,基于DO优化的系统频率波动最小。此外,基于DO优化参数的控制器有效地抑制系统频率的FFD、SFD和TFD,显著提高电网的稳定性和可靠性。

表6 不同方法获得的FFD、SFD和TFD

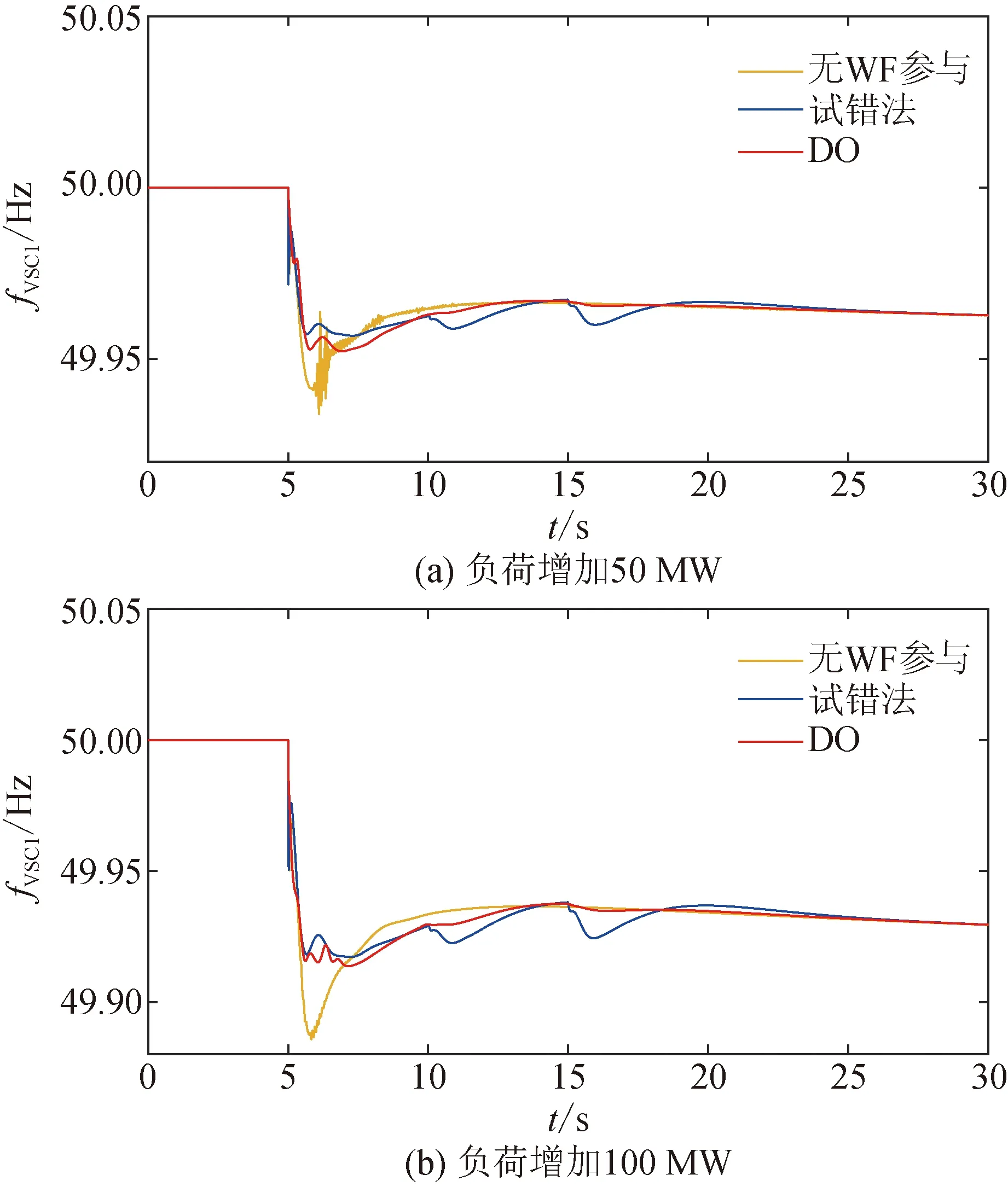
图8 在各种负荷增加变化下通过不同方法获得的频率响应

在本文所设仿真环境下,控制器参数优化过程所需时间约为10.9 h。值得注意的是,为更接近实际电网运行场景,在充分考虑多种因素下,该系统模型复杂,故离线优化与控制时间均较长。虽然本文针对三种不同负荷变化场景分别优化了三组不同参数,但在实际生产中,可根据具体场景可能出现的最大负荷波动情况离线优化出一组参数作为控制器的最终参数,以满足在线应用的实际需求。

4 结 论

本文针对多集群风机提出一种基于DO的控制参数优化策略,其贡献可概括为以下三点:

1)分别基于两个WF(各包括5台WT)提出梯次启动自适应惯性下垂控制策略,以实现电网系统频率支撑。其中,WF1中的WT按角速度被分为集群1和集群2。前者在负荷发生变化时立即参与频率调节,后者在前者的转子角速度恢复时运行,实现风机的梯次启动,进而显著减少一次、二次甚至三次频率跌落。

2)为了降低现场调参复杂度与试错法的不确定性,提高控制器的自适应能力,设计了基于DO的梯次启动自适应惯性下垂控制器参数设计框架,用于调整控制器的8个未知参数。

3)仿真结果表明,本文所提控制器参数优化框架与试错法相比,在各种负荷增加场景下均能获得良好的频率支撑效果。尤其是当负荷增加50 MW时,基于DO的SFD和TFD分别为0.0365 Hz和0.034 5 Hz,相比试错法(SFD和TDF分别为0.0411 0 Hz和0.040 0 Hz),稳定性提高了11.34%和13.74%。

本文仅考虑风电机组参与系统惯性和一次调频过程,时间尺度为10 s左右,因此在这一暂态过程中,可认为风速不变,风机出力大小不变;并且考虑到转速限制,认为载荷不会影响风机的调频能力。若要考虑更长时间尺度的调频控制策略,则风速随时间变化的特性不可忽略,这也是本文后续研究内容之一。