功能梯度材料板在热环境与横向载荷共同作用下的非线性振动分析

朱江辉,林华刚,张雪莉,常晓通

(1. 西北工业大学 自动化学院,西安 710072;2. 中国飞行试验研究院,西安 710089;3. 西北工业大学 力学与土木建筑学院,西安 710072)

功能梯度材料(FGMs)是一种专门为极限环境下工作而设计,具有理想性能的复合材料,因此广泛地应用在航空航天领域。FGMs的优点是它们可以在高热梯度环境中生存,同时能保持结构完整性。Jha[1]指出,用于特定应用的FGMs材料必须同时满足抗热载荷和机械载荷的能力。

很多学者对FGMs板的热弹性、静态和动态特性进行了研究。Loy等[2]利用3阶剪切变形板理论研究了FGMs壳、圆板在热、机械载荷耦合作用下的静、动力学响应。Woo等[3]研究了FGMs板壳在机械载荷和温度场作用下的大挠度问题,结果表明,热-力耦合效应是决定系统响应的主要因素。Ng等[4]选取了两个截断模态来研究FGMs板在平面内和周期激励下的稳定性,发现材料组成可以显著改变稳定区域的大小和范围。Javaheri等[5]在热场中讨论了FGMs板在面内载荷作用下的屈曲问题,给出了FGMs板的屈曲载荷和临界温度。夏贤坤等[6]对人环境中功能梯度材料剪切板屈曲后的自由振动进行了分析,讨论了材料组分指数、温度场等参数变化所带来的影响。燕秀发等[7]采用了半解析数值方法对线性梯度和指数梯度功能材料板分别受恒定位移、均匀拉伸载荷和弯曲载荷作用进行了分析。吴晓等[8]讨论分析了中性面位置、梯度指数、温度等因素对功能梯度材料圆板非线性振动及屈曲的影响。黄小林等[9]研究了轴向运动功能梯度材料板的自由振动与屈曲特性。

Hao等[10]研究了功能梯度板非线性动力响应,重点研究了横向荷载和面内激励作用下平板的1∶1内共振和参数共振。Kazemirad等[11]研究了轴向弯曲运动梁的热-力学非线性动力响应,特别考虑了3∶1内共振的特性。Yang等[12]研究了纵向循环载荷作用下不同边界的FGMs圆柱板的热场参数激励问题。Hamed[13]利用频率响应方程、相平面技术和Lyapunov方法研究了FGMs平板在混合激励下的非线性振荡和混沌动力学,分析了系统解的稳定性。郝育新等[14]研究了两对边简支另两对边自由的功能梯度板材料的周期与混沌运动。田建辉等[15]采用混合数值方法分析了功能梯度材料板中瞬态热响应问题。针对外载荷和温度载荷同时作用下,FGMs结构非线性主共振的动力学特性研究较少。

本文针对FGMs板非线性振动进行了研究,首先建立系统的非线性动力学模型,利用伽辽金方法将偏微分方程截断为常微分方程;采用多尺度法得到了系统的近似解析解和幅频响应;然后,研究了FGMs板在不同温度场下固有频率的变化及热屈曲问题,讨论了不同参数对FGMs板幅频响应的影响,当激励频率接近固有频率时系统的幅值急剧增大,系统呈现出硬特性,且存在多值和跳跃现象。通过数值解与解析解的比较,验证了分析的有效性。

1 理论分析

1.1 功能梯度材料

假设由陶瓷和金属材料组成的FGMs板,示意图如图1所示,在热环境下受到均匀分布的横向激励作用。板的宽度、长度和厚度分别为a,b,和h,陶瓷和金属的体积分数沿厚度方向分布为

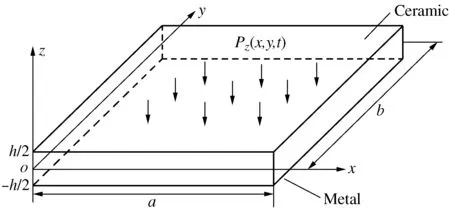
图1 功能梯度板示意图Fig.1 Schematic diagram of a functional gradient plate

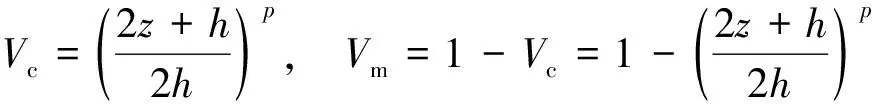
(1)

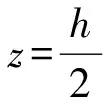
FGMs通过逐渐地改变材料成分的体积百分比含量而不使其在界面上产生突变,由于这种特殊的微观组织特征,从而使它的物理性能可以从低温侧的金属到高温侧的陶瓷进行平滑而连续的变化,可在极高温度梯度下工作。幂率公式用来计算FGMs的有效参数P(z,T)为

(2)

式中:PU,PL分别为FGMs板上表面和下表面的有效参数。FGMs有效材料属性:弹性模量E,泊松比ν,密度ρ和热膨胀系数α可以表示为温度的函数,即

P=P0(P-1T-1+1+P1T+P2T2+P3T3)

(3)

式中:T=T0+ΔT(z), ΔT(z)为厚度方向的温度增量;P0,P-1,P1,P2,P3是温度T(K)的系数。

E,ρ,α和ν可以进一步表示为:

(4)

1.2 运动微分方程

FGMs板的位移场可以用Reddy的3阶剪切变形理论来表示,即

(5)

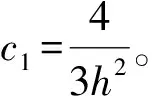
根据Von-Karman理论,非线性应变-位移关系为

(6)

将式(5)代入式(6),可以得到

(7)

其中:

当温度升高ΔT(z),FGMs板在热载荷作用下会产生热应变,则

(8)

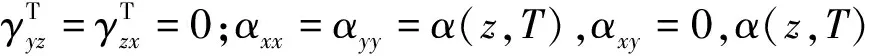
根据胡克定律,考虑到温度的影响,FGMs的应力-应变关系最终可以表示为:

(9)

其中:

根据哈密顿原理,可以建立运动方程为

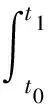
(10)

其中,应变能的变化δU可以表示为

τyzδγyz+τzxδγzx)dzdxdy=

(11)

板的内力可表示为:

(12)

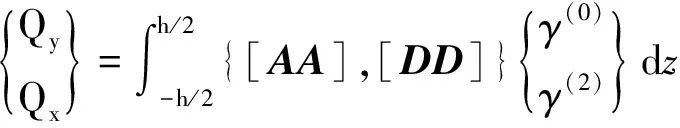
(13)

板的面内弯矩为:

(14)

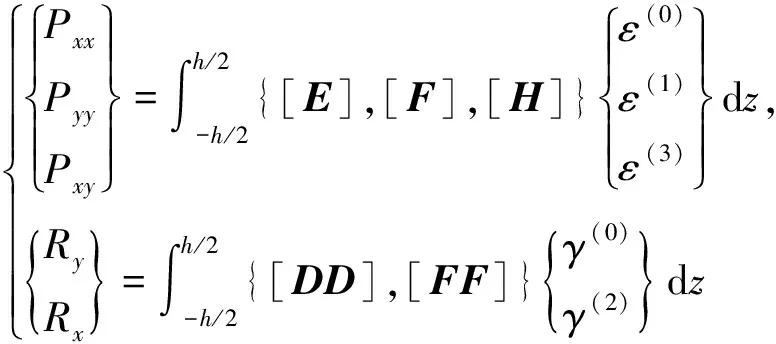
(15)

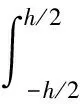
(16)

外荷载的虚功为

(17)

将式(11)、式(16)和式(17)代入式(10),可以得到:

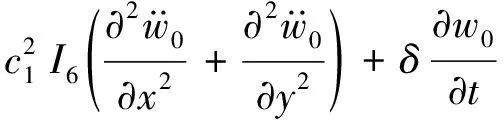
(18c)

(18d)

(18e)

四边简支壁板的位移函数可以表示为:

(19)

由于面内运动和旋转的惯量与横向运动的惯量相比很小,可忽略不计,因此平面内运动和旋转的位移可以用横向位移来表示。uij,vij,φxij和φyij可以通过式(18a)～(18e)由wij表达。将结果代入式(18c),得到FGMs板的控制方程为

ξ3w3(t)=k0p0cosωt

(20)

式中:Pz=p0cosωt,p0为外载荷的幅值;ω0为系统的固有频率;ξ1,ξ2和ξ3分别为系统的非线性系数。

1.3 热载荷

假定FGMs板在一个温度恒定的热环境中,温度只沿厚度方向变化。这是一维热传导问题,沿厚度方向的热传导方程为

(21)

热力学边界条件为

(22)

式中:ΔTU和ΔTL分别为上层和下层变化的温度。

式(21)的解为

T(z)=T0+ΔT(z)

(23)

对于 FGMs 板,则有

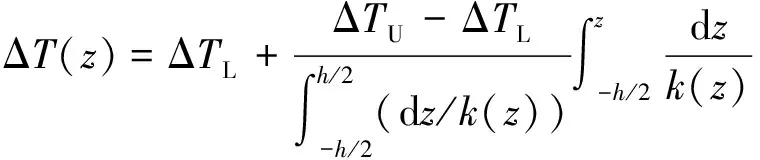
(24)

2 主共振分析

(25)

其中:

对于主共振问题,引入小参数ε,令η1=2με2,η2=α2ε,η3=α3ε2,k=Kε2。式(25)可以改写为

(26)

采用多尺度法求解式(26),得到2阶近似解。引入调谐参数σ,Ω=1+ε2σ。式(26)的近似解为

(27)

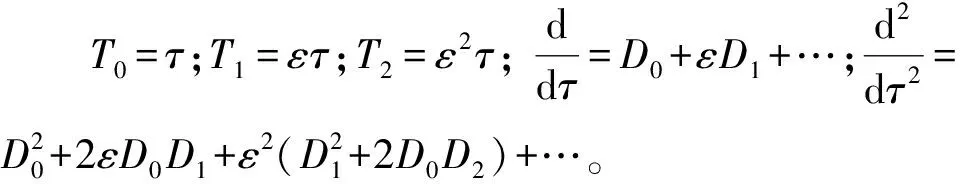
将式(27)代入式(26),可得:

(28)

式(28)中第一个方程的解为

(29)

式中cc为共轭项。将式(29)代入式(28)中第二个式子,则

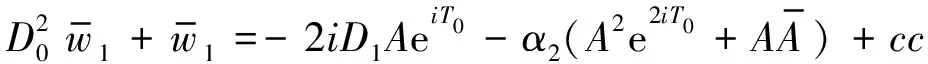
(30)

D1A=0 orA=A(T2)

(31)

则式(30)的解为

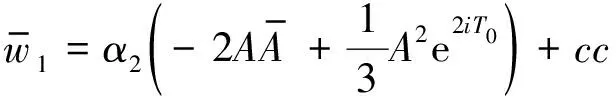
(32)

将式(32)代入式(28)中的第三个式子,有

eiT0+cc+NST

(33)

NST包含e±3iT0的比例项,消除久期项,则

(34)

式(31)可以表示为复合函数的形式,则

(35)

将式(35)代入式(34),将实部与虚部分离,则:

(36)

令(σT2-β)=γ,对应于系统的稳态运动,α′=0,γ′=0,则:

(37)

消除γ,可以得到系统频率响应方程为

(38)

3 解的稳定性分析

考虑系统在稳态运动中的稳定性问题,则

α=α0+α1,γ=γ0+γ1

(39)

对小扰动α1和γ1进行泰勒展开,得到1阶线性近似为:

(40)

将原系统周期解的稳定性分析转化为系统零解的稳定性分析。式(40)的特征方程为

(41)

可以写为

λ2+c1λ+c2=0

(42)

其中:

式(42)的特征值可以表示为

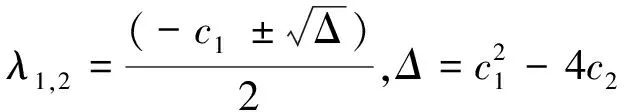
(43)

根据Routh-Hurwitz准则,当μ>0时,可以得到系统稳定的重要条件

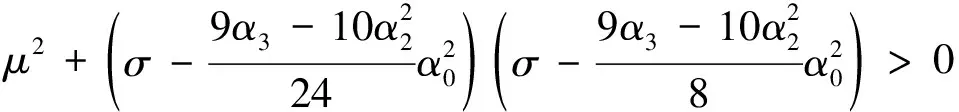
(44)

4 数值结果

以简支FGMs平板为例,对结构进行屈曲和非线性振动分析。随温度变化的弹性模量E, 泊松比为ν, 密度为ρ,热膨胀系数为α,导热系数为k,具体参数见表1。

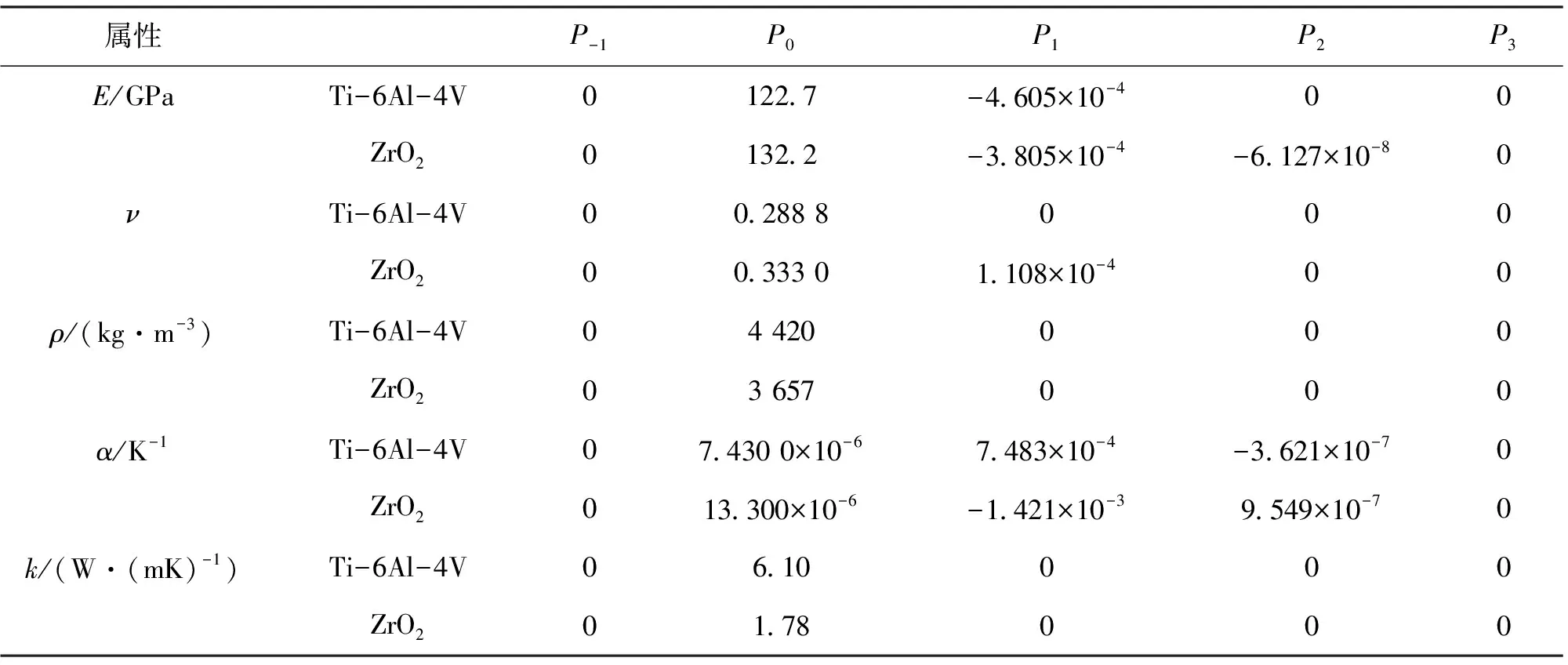
表1 FGMs材料参数Tab.1 Material parameters of FGMs

4.1 参数分析

首先对3种工况下温度对FGMs板性能的影响研究。工况1:室温(300 K, 图2a));工况2:ΔTL=0,ΔTU=300 K(图2b));工况3:ΔTL=ΔTU=300 K(图2c))。发现,弹性模量不再是沿厚度方向的固定值,高温使材料的弹性模量显著降低。当板结构上下表面存在温度差时,弹性模量逐渐减小,当体积分数小于1时,弹性模量在中间位置出现峰值。

图2 弹性模量沿厚度方向的变化Fig.2 Changes of elastic modulus along thickness direction

FGMs板中当p=2时不同热环境下弹性模量和热膨胀系数的变化曲线(图3,图4)。温度越高,弹性模量越小。在图4中,对于金属材料,温度越高,热膨胀系数越大,而对于陶瓷材料,结果恰恰相反。对于热膨胀系数,在中间位置有一个交点。

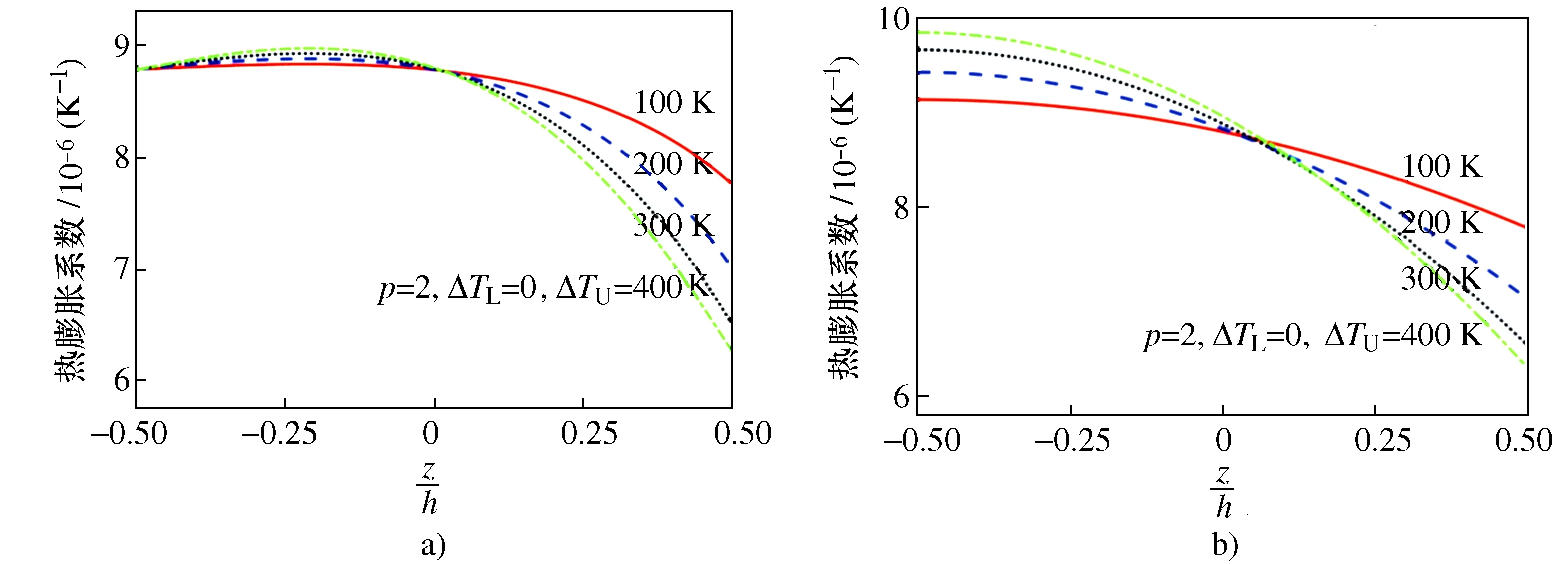
图4 不同热环境下热膨胀系数的变化Fig.4 Changes of thermal expansion coefficient under different thermal environments

4.2 模型验证

简支平板的频率方程为

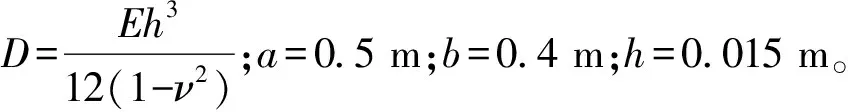
当p分别为0和100%时,陶瓷和金属材料平板的频率如表2所示。

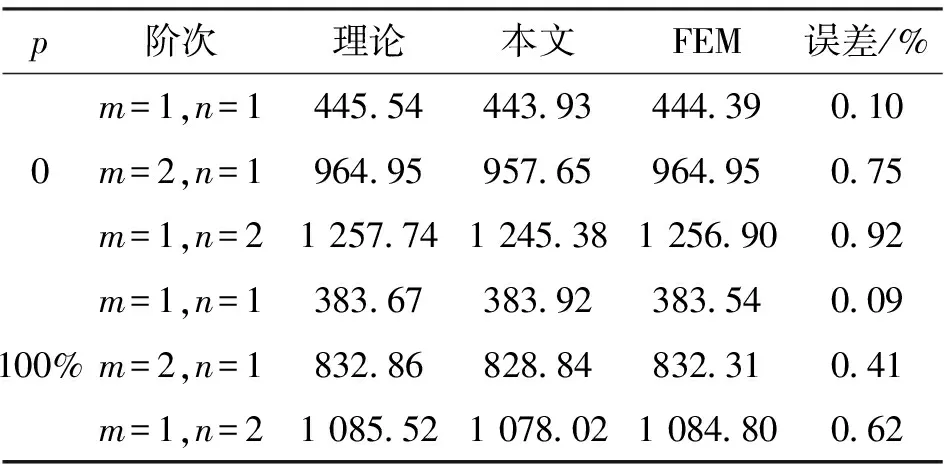
表2 平板的频率 Tab.2 Frequency of the plate Hz

Ansys计算的系统固有频率与理论值吻合,随着阶数的增加,相对误差略有增加,但不超过1 %。表3显示,FGMs板频率随着金属体积分数的增加,前两阶频率逐渐减小。当体积分数达到10%时,频率变化很小。

表3 不同体积分数的FGMs板频率Tab.3 Frequency of FGMs boards with different volume fractions

4.3 温度对结构特性的影响

当热环境设置为ΔTL=0,ΔTU≠0,FGMs板的频率列于表4和表5。发现,随着温度的升高,结构的固有频率降低,这主要是由于结构的弹性模量降低引起的。当温差达到735 K,最高温度达到1 035 K(室温为300 K)时,结构发生热屈曲。当p=2时,频率显著降低,屈曲温差为456 K,低于单一材料壁板在p=0时的屈曲温差。

表4 FGMs平板频率随温度变化(p=0)Tab.4 Variation of FGMs plate frequency with temperature (p=0,ΔTL=0,ΔTU≠0)

表5 FGMs平板频率随温度变化(p=2,ΔTL=0,ΔTU≠0)Tab.5 Variation of FGMs plate frequency with temperature(p=2)

当热环境为ΔTL=ΔTU时,板的频率如表6与表7所示。在相同体积分数下,结构热屈曲温度明显小于ΔTL=0工况。当ΔTL=0,ΔTU≠0时,屈曲温度随体积分数的变化如表8所示,屈曲温度随金属体积分数的增加而降低。

表6 FGMs平板频率随温度变化(p=0,ΔTL=ΔTU)Tab.6 Variation of FGMs plate frequency with temperature(p=0)

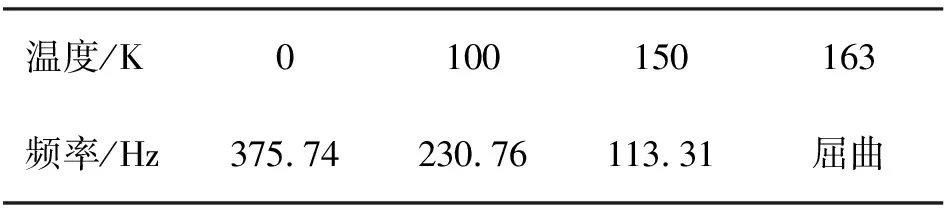
表7 FGMs平板频率随温度变化(p=2,ΔTL=ΔTU)Tab.7 Variation of FGMs plate frequency with temperature(p=2)

4.4 系统参数对幅频响应的影响

激励幅值、阻尼、体积分数和厚度对幅值频响的影响如图5所示。

图5中,黑色粗线为稳定解,红色线为不稳定解。当激励频率接近固有频率时,幅值迅速增大,支撑曲线族的骨架向着频率增大的方向弯曲,表现出硬特性,而且存在多值和跳跃现象,表现出典型的非线性动力学特征。当激励幅值增大时,阻尼减小,体积分数增大或厚度减小,相同激励频率下稳定解明显增大。随着厚度的减小,共振区域逐渐变宽,而对应相同的频率,且共振被激发的条件下,稳定解的幅值随板厚度的减小有明显的增加。以h=0.012 m的幅频曲线为例,当激励频率达到一定值时,曲线存在着多值和跳跃现象。在激励频率远离固有频率的情况下,系统频率与振幅存在一一对应的关系,也就是说,系统只有唯一解,且由解的稳定性判别条件可知,这个解是稳定的。

4.5 温度对幅频响应的影响

随着温度的升高,结构响应的共振区域会变宽,如图6所示。温差越大,稳定解的最大振幅越大。ΔTL=ΔTU=100 K状态下的幅值大于ΔTL=0,ΔTU=100 K状态下幅值,表现出硬特征,响应曲线存在着多值和跳跃现象。在共振频率处,频率响应幅值显著增大,温度的变化带来了显著的非线性现象。

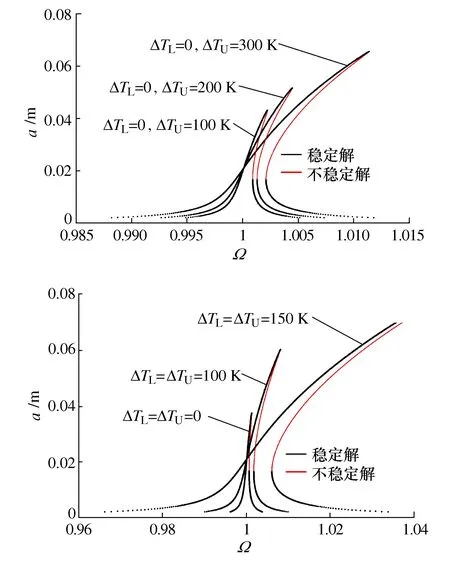
图6 不同温度条件下幅值频率响应曲线Fig.6 Amplitude frequency response curves under different temperature conditions

结构的幅频响应数值解如图7所示。当激励频率从低到高扫描时,系统响应幅值随着频率升高逐渐增大。当频率进一步升高时,曲线会从A点跳到B点,振幅会突然减小。响应幅值随Ω的增加而减小。振动的幅值随着激励频率的增加,在A点处的幅值最大。当激励频率由高向低反向扫描,刚开始时的响应幅值增大,然后从C点到D点发生跳变。在D点出现拐点,振幅减小。使用本文方法的解析结果与数值结果吻合较好,证明了主共振频响方程的正确性。图8可以看出,稳态响应幅值接近于平板的厚度,而体积分数对周期运动幅值影响不大。

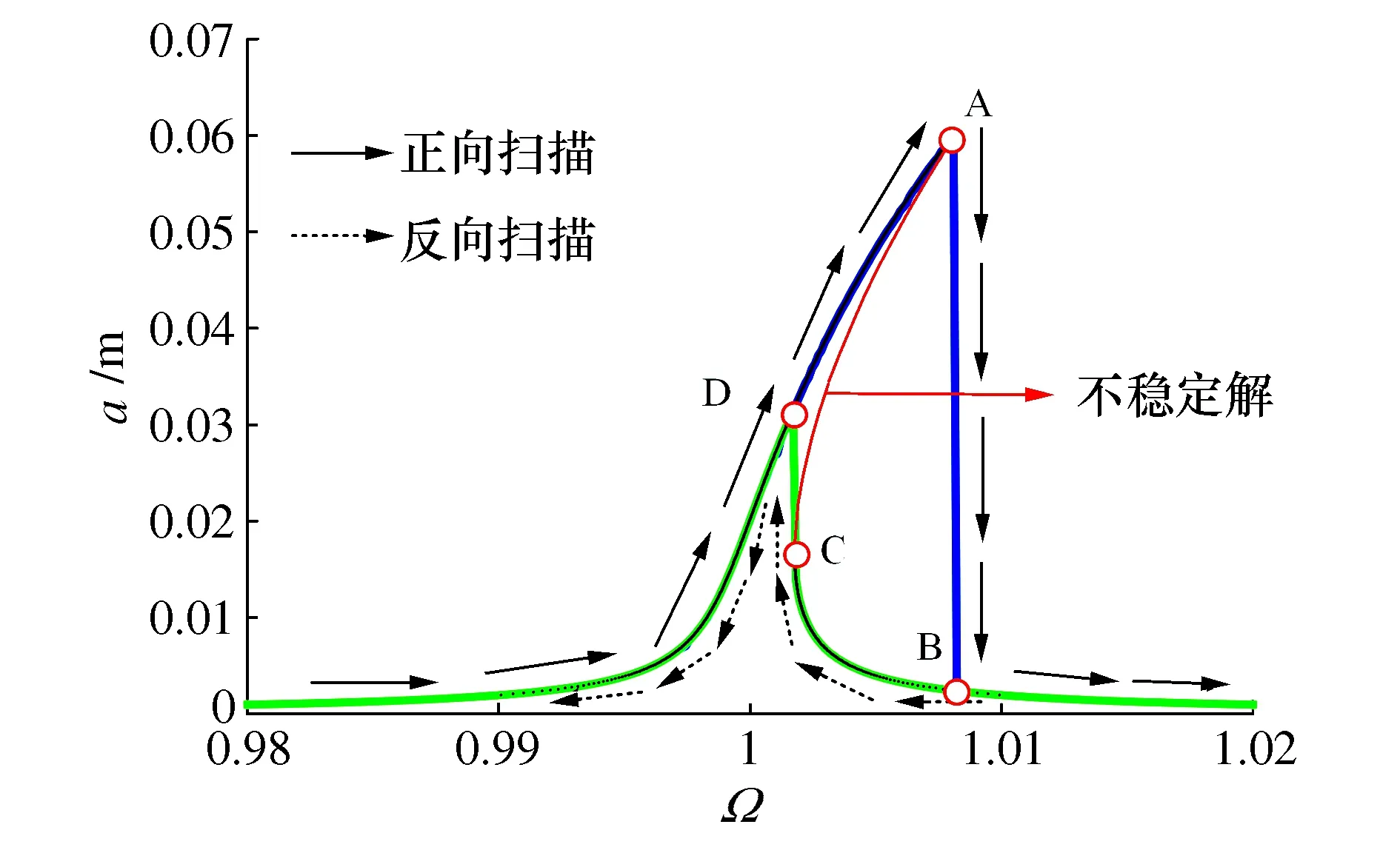
图7 幅频响应Fig.7 Amplitude-frequency response

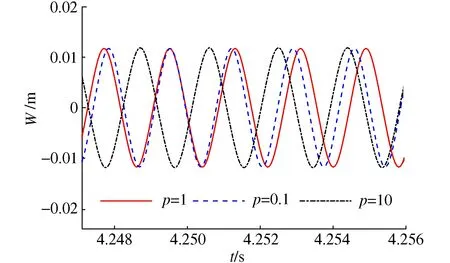
图8 时程曲线 Fig.8 Time history curve

6 结束语

本文研究了横向激励和热载荷作用下FGMs板的主共振和稳定性。采用多尺度法得到了系统的主共振和幅频响应方程。通过数值解与解析解的比较,说明了主共振幅频响应方程的正确性。结果表明,在温度载荷作用下,结构的固有频率减小,屈曲温度随金属体积分数的增加而降低。当激励频率接近固有频率时系统的幅值急剧增大,支撑曲线族的骨架朝频率增大的方向弯曲,呈现出硬特性,而且存在多值和跳跃现象,表现出典型的非线性运动学特征。