商业建筑重特大火灾事故防控策略分析

闫金花讲师

(西南科技大学 土木工程与建筑学院,四川 绵阳 621010)

0 引言

商业建筑内部空间大,火灾荷载大,没有或缺少实体分隔,火灾从初起到蔓延的过程发展迅速,火势猛烈,扑救难度大,造成的损失也很大。目前,我国面积大于5万m2的大型商业综合体超过5000座,其中10万m2以上的超过1400座,且仍呈继续增长态势[1]。对于建筑火灾风险的研究主要集中于对单体建筑火灾风险的评估,如Hansen等[2]建立一种火灾风险模型(Fire Risk Model),可根据高层建筑的建筑特征、消防安全特征对居住者的生命安全水平和财产损失风险水平进行评估;Li等[3]提出高层建筑火灾评估指标体系,并采用灰色关联度、层次分析法和模糊评估法建立数学模型,可应用于高层建筑火灾风险分析中;Matellini等[4]提出利用贝叶斯网络模型研究住宅火灾,以提高住宅火灾安全评估的可信度。这些研究多集中于高层建筑和住宅,较少涉及商业建筑,而且主要是针对单体建筑进行火灾风险评估,不能对目前已有建筑尤其是商业建筑的总体消防灭火水平进行有效评估,而且很多指标在评估过程中过度依赖专家的经验和知识背景。由于各位专家的研究领域及工作性质不同,因此在评估过程中无法更客观和全面地进行指标打分,从而影响了评估结果的准确性。

我国在消防灭火方面的研究多集中于消防灭火战略战术的研究和消防管理对策分析,对灭火过程中的隐患研究甚少。笔者认为灭火过程不应只包含消防灭火这一个阶段,还应该从系统、发展的观点来看待消防灭火过程。从发现火灾到灭火的全过程中,存在诸多影响因素,如火灾自动报警、初期人员报警、灭火装备、灭火条件等,这些都有可能导致灭火的失败。本文通过对已发生重特大火灾事故的商业建筑进行消防灭火分析,建立火灾模糊故障树模型[5-6],数据分析方面采用区间上的L-R型模糊数的分布函数作为模糊故障树中基本事件概率的隶属函数[7-8],然后通过模糊故障树分析,得到系统模糊数的总体概率分布函数,最后通过敏感度分析,给出商业建筑灭火过程的防火策略,从而有效消除大空间商业建筑的消防隐患。

1 消防灭火故障树模型

特别重大火灾指造成30人以上死亡,或者100人以上重伤,或者1亿元以上直接财产损失的火灾;重大火灾指造成10人以上30人以下死亡,或者50人以上100人以下重伤,或者5000万元以上1亿元以下直接财产损失的火灾(源自公安部办公厅公传发[2007]245号《关于调整火灾等级标准的通知》)。通过对我国商业建筑重特大火灾事故进行统计调查,全过程分析消防灭火失败的原因,可知:消防灭火与火灾自动报警时间是否延迟、初期人员报警延迟、室外消火栓是否有效发挥作用、消防装备条件、起火位置隐蔽、灭火条件、施工现场是否有人监管、消防通道是否畅通、建筑物内是否设置有消防电梯、安全通道是否上锁等情况都有关联。当灭火时间延迟和灭火条件不具备同时发生时会导致消防灭火失败,而灭火时间延迟是由火灾报警时间延迟或报警后消防车到达延迟造成,火灾报警时间延迟是由初期火灾发现延迟或人员报警延迟造成,初期火灾发现延迟是由火灾自动报警系统报警失败且人员察觉火灾发生时间延迟造成。火灾自动报警系统报警失败是由未安装火灾自动报警系统或安装后被拆除等基本事件造成,用b1,b2,…,b6表示;人员察觉火灾发生时间延迟是由值班人员未及时巡查等基本事件造成,用c1,c2,c3表示;人员报警延迟是由报警电话未设置或设置不当等基本事件造成,用l1,l2,…,l4表示;灭火条件不具备是由消防通道不畅等基本事件造成,用l5,l6,…,l16表示。报警后消防车到达延迟和灭火战术不适当为非基本事件,不做讨论,由此建立商业建筑消防灭火失败故障树模型,如图1。

2 故障树模糊分析

2.1 隶属函数

为确定系统中各基本事件的概率,需要选用合适的模糊分布来确定其模糊数的隶属函数。考虑到各基本事件的概率是在[0,1]之间的某一值左右波动,选用中间型的模糊分布较为合适。在中间型模糊分布中,线性分布的基本事件发生概率的模糊数是直线与横轴的2个交点之间的区间,其隶属度在[0,1]之间变化,而在这一区间外点的隶属度为0;在非线性分布中,基本事件概率分布在某一点处为峰值点,其隶属度为1,由该峰值点处向左、右无限延伸,取概率值[0,1]之间的各点的隶属函数作为基本事件概率的模糊分布,不存在隶属度为0的点[9-12]。由于火灾数据的缺乏,无法判定基本事件概率模糊数中隶属度为0的点,无法将其概率限制在某一区间内,因此,选用非线性的模糊分布较为合适,考虑到基本事件概率是在[0,1]之间的某一值附近波动,于是选取[0,1]区间上对称的L-R型模糊数的分布函数作为模糊故障树中基本事件概率的隶属函数,记为(m,α,β),m为模糊数的均值,α、β为模糊数的左、右分布,概率均值的隶属度取1。

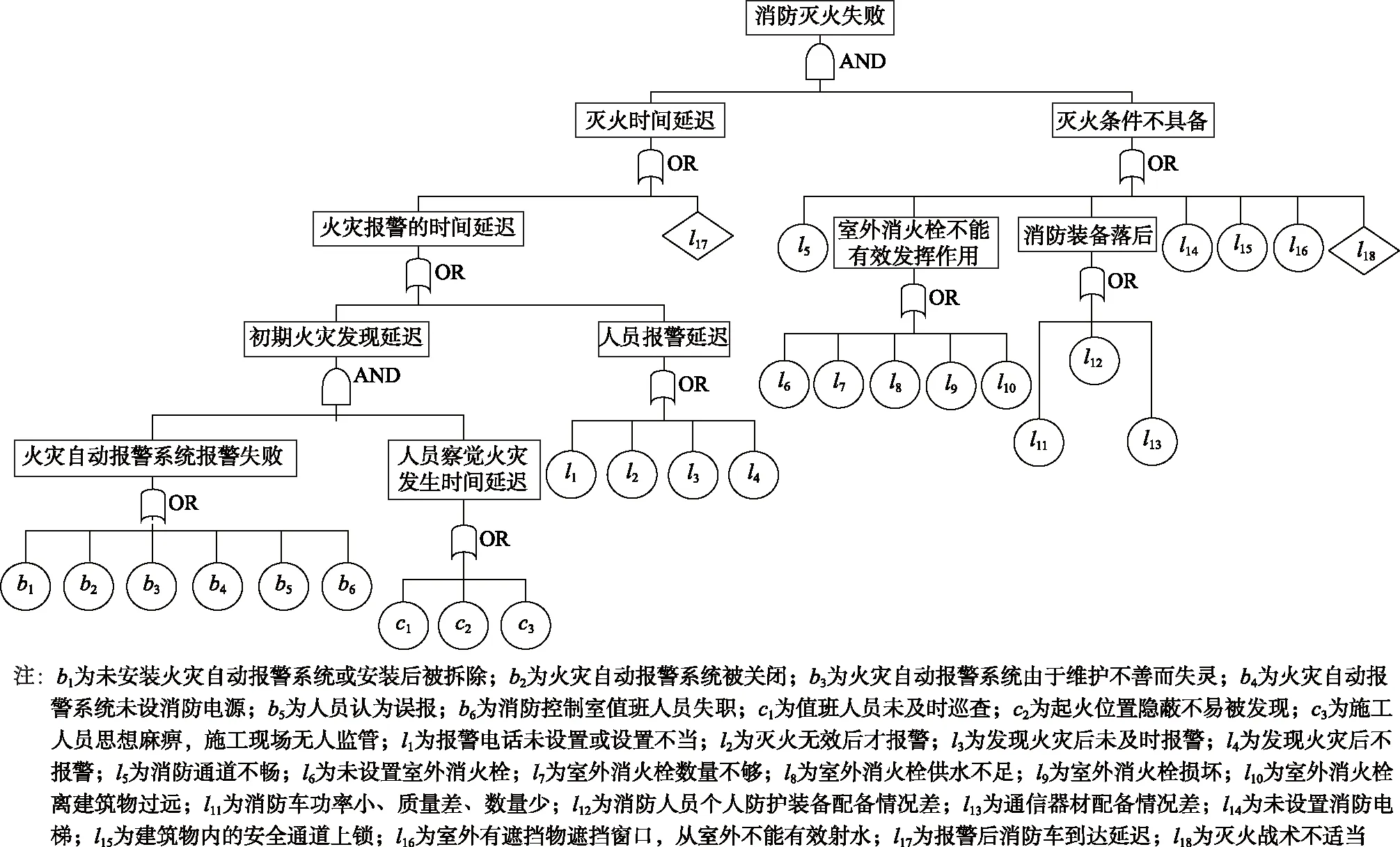
图1 商业建筑消防灭火失败故障树Fig.1 The fault tree for the fire extinguishing in commercial buildings

x∈R

(1)

x∈R

(2)

x∈R

(3)

其中,mj,mk,mn分别为基本事件bj,ck,ln概率模糊数的最大似然估计。

图2 基本事件模糊数的分布Fig.2 The of distribution of the fuzzy number of the basic events

2.2 总体概率分布函数

商业建筑消防灭火失败故障树的结构函数为:

ψ=[(b1+b2+…+b6)·(c1+c2+c3)+(l1+l2+l3+l4)]·(l5+l6+…+l16)

其中:b1与b2,…,b6之间互斥,b2,…,b6之间相互独立;c1,c2,c3之间相互独立;l1,l2,l3,l4之间相互独立;l6与l7,…,l10之间互斥,l7,…,l10之间相互独立;l5,l11,…,l16之间相互独立。

总体概率分布函数为:

(4)

2.3 敏感度分析

应用泛函分析中距离的概念定义模糊敏感度,从而反映出模糊集之间的整体差异。

1 若U={u1,u2,…,ur}是有限集,定义

(5)

2 若U=[a,b]是实数集上有限闭区间时,定义

(6)

对于有界模糊数,可以利用模糊数的中值来计算模糊重要度。

可推导得:

(7)

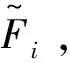
仍为有界模糊数,其中值为mTe[19～21]。

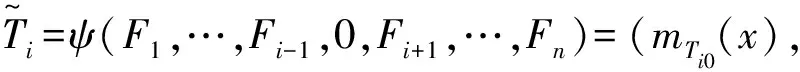
STi=mTe-mTie≥0

(8)

3 应用分析

调查并分析商业建筑特大火灾案例情况[22],根据公式(1)-(3),得到消防灭火失败故障树各基本事件模糊数的均值及左、右分布,见表1。

表1 基本事件模糊数的均值及左、右分布Tab.1 The mean value, and the left and right distributions of the fuzzy number of basic events

由式(4),得到商业建筑消防灭火失败模糊故障树总体概率分布函数:

根据式(7)、(8),得到商业建筑消防灭火失败故障树各基本事件的模糊敏感度,见表2。

对基本事件的模糊敏感度结果进行分析得知:

(1)c1事件——值班人员未及时巡查对消防灭火的影响最大;其次是b1事件——未安装火灾自动报警系统或安装后被拆除,两者对灭火失败模糊故障树顶事件的影响最大,影响的模糊敏感度数量级达到10-1。

(2)在人员察觉火灾发生的时间延迟事件中,l3事件——发现火灾后未及时报警对故障树顶事件的影响最大,影响的模糊敏感度数量级达到10-2。

表2 基本事件的模糊敏感度Tab.2 The fuzzy sensitivity of basic events

(3)在消防装备落后事件中,l11事件——消防车功率小、质量差、数量少,l12事件——消防人员个人防护装备配备情况差对故障树顶事件的影响最大。

(4)在室外消火栓情况中,l8事件——室外消火栓供水不足对消防灭火的影响最大。

(5)在火灾自动报警系统中,b2事件——火灾自动报警系统被关闭对故障树顶事件的影响最大。

(6)施工过程中的c3事件——施工人员思想麻痹,施工现场无人监管的问题突出。

(7)在消防设施中,l5事件——消防通道不畅问题最突出。

(8)c2事件——起火位置隐蔽,不易被发现,如吊顶等处火灾发生时不易被发现,当人员察觉到火灾发生时,往往火灾已经发展到难以扑灭的程度。虽然对消防灭火影响较小,但火灾发现晚造成的损失较为严重,因此,针对这一点,应注意预防。

综上分析,结果与实际相符,报警延迟对消防灭火的影响最大,因此大空间商业建筑首先应加强日常人员的巡查工作,发现火灾及时报警,同时安装火灾自动报警系统并保证其处于开启状态;其次应改善消防灭火装备以及消防车、消防人员个人防护装备配备情况;最后应解决室外消火栓供水不足的问题,这样才能有效地提高商业建筑消防灭火的可靠度。

4 结论

(1)通过对已发生重特大火灾事故的商业建筑进行分析,建立了商业建筑消防灭火模糊故障树模型,评估了我国目前商业建筑的总体消防灭火水平。

(2)找到已建商业建筑内部确实存在的消防隐患,通过模糊敏感度分析,给出了商业建筑消防灭火的策略,可以有效地提高商业建筑消防灭火的可靠度。

(3)所建立的模型对于商业建筑的灭火处置和灭火过程中所遇到的困难没有做更多的讨论,还可以做进一步的细化研究,使模型趋于更加完善。