基于机器学习的低弹性模量钛合金建模和预测的研究
潘 登, 李 谦, 李 强
(1. 上海大学 材料基因组工程研究院, 上海 200444;2. 上海理工大学 机械工程学院, 上海 200093)
目前,钛合金已经在人工关节、牙科种植和外科器械中得到了广泛使用,但是钛合金的生产工艺相对复杂,加工难度大,造成成本较高,限制了其广进一步发展[1]。目前,大范围使用的钛合金成分为Ti-6Al-4V 合金(TC4 钛合金),医学临床研究发现,TC4 钛合金在人体内会向血液释放Al 离子和V 离子,这些离子会诱发阿尔兹海默症、神经系统病变、骨骼软化症等疾病。TC4 钛合金的弹性模量远高于人骨的,因此,会造成“应力屏蔽”现象,不利于新骨的生长。近年来,通过加入不同配比的合金元素(如Ta、Mo、Nb),获得匹配人骨弹性模量的高强度无毒β 型钛合金是目前医用材料研究的重要方向之一[2]。
计算相图是一种常用的设计方法,它基于热力学平衡原理和试验数据,并结合了计算机模拟和优化算法,旨在提供对合金体系中各种相的形成和稳定性的深入理解。尽管计算相图方法在预测和计算相图方面非常有用,但它仍然依赖于试验数据和热力学数据库的准确性。钛合金的制备和加工较为复杂,组成元素种类繁多,大幅增加了材料性能试验量,所以会造成上述性能测试方法成本高、周期长、效率低,给新型钛合金的开发带来了诸多挑战。
基于数据驱动方式的机器学习建模无需明确内部的复杂机制,仅依靠数据训练来构建关系模型,目前已成为材料研究的热点之一[3-5]。主要的机械学习方法有多层感知器(multi-layer perceptron,MLP)、卷积神经网络(convolutional neural networks,CNN)、随机森林网络(random forest regression,RFR)等。MLP 是一种常见的前馈神经网络模型,由多个节点组成的多个隐藏层构成,每个节点都是一个人工神经元,接收来自前一层的输入,并将加权和输入进行非线性变换后传递给下一层[6]。CNN 是一种依靠卷积核从输入数据中提取局部特征,并通过卷积核的滑动获得输入数据特征图的神经网络[7]。RFR 是一种集成学习方法,通过组合多个决策树模型来进行预测和分类[8-9]。采用机器学习的方法,是从数据和算法的角度建立模型,揭示数据和性能的相关性和显著性,在合金成分设计和性能预测方面具有一定的指导意义[10-13]。
上世纪80 年代末,日本学者Morinaga 等[14]提出,采用反映元素电负性的d-电子结合能(Md)和反映d 轨道电子结合强度的d-电子结合次数(Bo)来评估元素原子尺寸、电负性及合金化等因素的影响。各合金元素的Md和Bo按照原子分数取加权平均值,即为合金的d-电子平均结合能()和d-电子平均结合次数()的影响水平。根据计算结果可以确定合金的相稳定性,为合金设计提供理论依据。Mo 当量([Mo])常被用于钛合金中确定β 相的稳定程度。本文针对钛合金弹性模量快速预测的需要,利用已有的钛合金弹性模量,并通过合金设计公式转换得到钛合金的[Mo]、、三种参数作为原始数据;基于数据驱动建立钛合金元素配比与其弹性模量关系模型,并对模型预测性能进行验证与对比分析。
1 机器学习过程
1.1 合金元素数据转换与分析
基于钛合金设计公式及机器学习的多层感知器理念建立数学模型,利用模型揭示钛合金元素配比与弹性模量之间的关系。图1 是模型数据集转换流程。
首先,数据集收集具有β 相的钛合金数据,使用箱型图描述这个数据集的样本分布,横轴为不同参数的名称,纵轴为相应元素参数值;然后,利用相应公式转换成为、、[Mo]三种参数作为相关模型原始输入数据直接进行处理,转换公式为:
式中:xi为 合金元素i的 原子分数; (Bo)i为合金元素i的Bo值; (Md)i为合金元素i的Md值[15]。在数据集进行转换之后依旧使用箱型图描述这个数据集的样本分布,用来分析数据集的稀疏值和异常值。
数据集经过转换后,只有[Mo]、3 个输入标签值,利用斯皮尔曼(Spearman)计算方法来获得三者与弹性模量之间的相关性热力图与相应的P值判断相关性的显著程度。
通过Spearman 计算所得的P值是用于衡量两变量相关性是否具有统计学上显著性的指标。Spearman 相关性系数衡量了两个变量之间的线性强度,取值范围为-1~1。
相关性ρ计算公式如下:
式中:R(x)为x元素的当前取值;R(y)为y元素的当前取值;为x元素的平均值;为y元素的平均值;n为元素观测总数。
在训练过程中,所有模型将数据集按照8:2 的比例进行分割,其中80%用于模型训练,20%作为测试集验证模型性能。为提升模型在训练过程中的收敛速度,将数据集送入模型前进行归一化处理,并采用式(5)将输入量归一化至区间[0, ε],采用式(6)将输出量归一化至区间[-ε, ε]。
式中:x、y分别为转化后的输入标签值以及合金的弹性模量;x′、y′分别为归一化后所得相应输入、输出值; ε为缩放系数。
钛合金中,钛占比一般不超过80%,因此,本文将 ε设定为0.8。
1.2 机器学习模型的建立
本文分别使用CNN、RFR 和MLP 三种模型,通过Python 软件进行建模和计算。
1.2.1 MLP 模型
图2(a)为MLP 模型的训练示意图,其中,输入层接收原始数据或特征向量作为输入,隐藏层进行加权和非线性变换,输出层根据具体任务产生相应的输出结果。隐藏层和输出层之间的连接由权重参数决定,各层之间皆使用激活函数进行连接,这些参数通过训练进行优化。
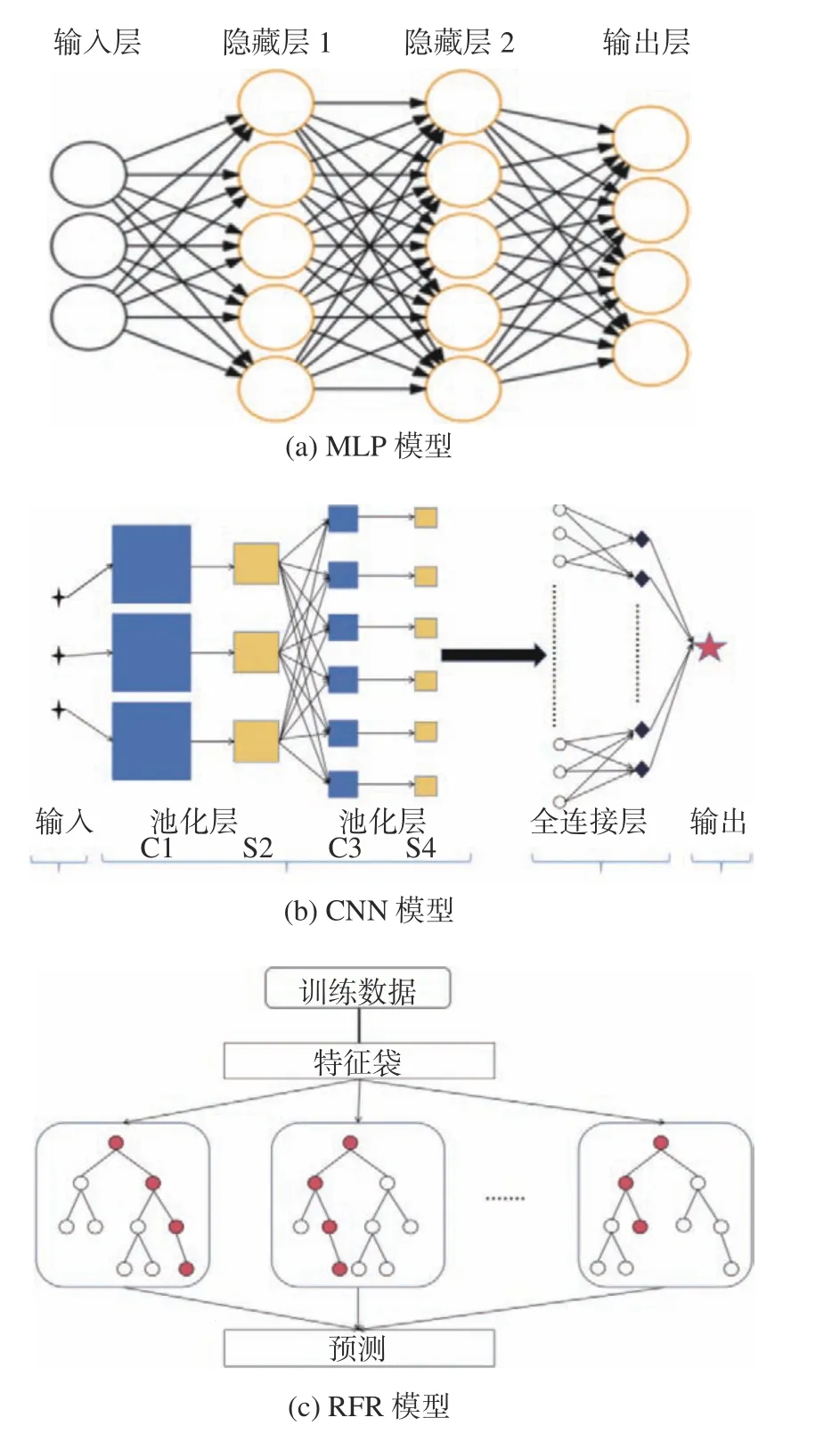
图2 三种模型内部结构图Fig. 2 Internal structure diagrams of the three models
MLP 模型的核心思想是通过非线性变换(通常是使用激活函数)将输入数据映射到更高维的特征空间。MLP 模型的训练方法通常使用反向传播算法,该算法通过计算损失函数对于权重参数的梯度,不断调整权重参数以最小化损失函数。具体表达如下:
式中:y为输出值;hk为输出层神经元的输入加权和。R为使用的激活函数为整流线性函数(rectified linear unit,R),其表达式为:
在神经网络中,R函数的导数恒为1 或0,不存在梯度消失的问题,因此,能够更好地训练深层神经网络。R函数在输入值为负时输出为0,因此,可以使神经网络中的一部分神经元处于关闭状态,增加了网络的稀疏性,减少了模型的复杂程度[16]。
1.2.2 CNN 模型
CNN 模型(见图2b)在经过多个卷积、池化操作后,能挖掘数据中隐含的深层特征[17-18],CNN模型中卷积层公式如下:
式中:W为图像宽度;H为图像高度;S为卷积核步长;p为图像边缘增加的边界像素层数。
在CNN 模型中,输入数据只能是图片,所以对于转换后的合金元素数据进行图像化三维处理,随后放入CNN 模型中进行训练。
1.2.3 RFR 模型
RFR 模型(见图2c)通过构建多个决策树,并对它们的结果进行综合,从而提高了整体预测的准确性和稳定性。每个决策树都是独立的分类器,最后预测结果由所有决策树的投票或平均所决定。RFR 模型的优点包括具有处理高维数据和大规模数据集的能力、对缺失值或异常值的鲁棒性较强、参数调整需求较少[19-24]。
1.3 机器学习模型的预测
为量化各个预测模型在验证集上的预测性能,评价指标采用相关指数(r-square,R2),均方根误差(root mean square error, RMSE)两种性能指标对模型性能进行量化,RMSE 指标越小表明模型预测性能越优,R2 指标越趋近于1,则模型预测能力越具有可信度,R2 指标公式如下[25-28]:
式中:yi为 观测值;为回归模型预测值;为所有实际观测值的均值。
RMSE 公式如下:
式中:ti为 每一批次计算过程中的标签;yi为每一批次计算过程中的输出。
所有模型训练完成后,储存相关系数和权重,将数据集中20%未经训练的数据作为验证数据放入模型中进行验证,通过比较其RMSE 和R2 指标来判断各个模型的优劣[28]。
RFR 模型作为机器学习模型在参数确定的情况下,预测性能指标均为确定值[29-31],而CNN 模型和MLP 模型具有特殊的结构,对具有神经网络结构的模型进行多次预测,对预测结果取平均值,比较性能优劣来判断模型预测性能。本文将分别对CNN 模型、MLP 模型进行5 次训练和预测[32-35]。
2 结果与讨论
2.1 数据集分析
图3 为未转换前数据的箱型图。在数据集中,钛合金中的Ti 最大质量分数为88.2%,弹性模量分布在24.7~116.0 GPa。图3 中除了Ti 以外,Nb 质量分数中位数高于其他合金元素,它是开发低弹性模量钛合金时添加最多的合金元素。其次是Zr,它与Ti 同属一族,具有与Ti 相似的物理化学性质,可用于强化合金和调整β 相稳定性。数据集中,三元和四元钛合金最多,所以,钛合金数据集中一组合金成分常常缺失一种或多种合金元素,从而导致数据集具有较强的稀疏性。由于这些合金元素在数据集中稀疏性太大,所以它们配比中位数接近零。需要指出的是,稀疏性太大的数据集对于神经网络训练是非常不利的。

图3 数据集未转换前合金元素统计箱型图Fig.3 Statistical box plot image of the alloy elements before dataset conversion
图4 是数据集转换后参数统计箱型图。图4 中除了[Mo]参数以外,、两个输入值几乎没有异常数据,通过钛合金成分设计公式转换得到的数据集稀疏性减少,为模型的训练提供更适合的原始数据,更有利于模型的训练和拟合。
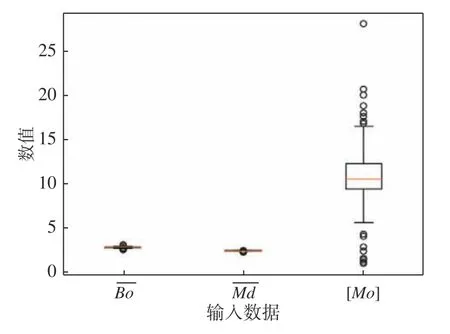
图4 数据集转换后参数统计箱型图Fig. 4 Statistical box plot image of the parameter after dataset conversion
2.2 参数与弹性模量的相关性分析
图5 是采用Spearman 系数计算数据集各参数同弹性模量所得的相关性系数的热力图。如果计算得到的Spearman 相关性系数具有较小的P值(通常小于选定的显著性水平,如0.05),则可以认为观察到的相关性系数不太可能是由随机因素导致的,存在着真实的相关性。这意味着可以拒绝零假设,并认为两个变量之间存在显著的线性相关性。由图5可知,[Mo]与钛合金的弹性模量(E)相关性最大,相关性系数为0.29。在本文数据集中反映出[Mo]与弹性模量呈正相关;在数据集中与弹性模量的相关性系数为-0.22,说明与弹性模量之间呈负相关;与弹性模量相关性系数为-0.10,说明与弹性模量呈负相关。

图5 采用Spearman 系数计算数据集各参数同弹性模量(E)所得的相关性值的热力图Fig. 5 Heat chart of the Spearman coefficient-calculated correlation value between each parameter in the dataset and elastic modulus (E)
表1 是通过Spearman 计算所得数据集之间的P值,弹性模量与[Mo]、之间的相关性<0.05,它们之间具有显著的相关性。与弹性模量的P值>0.05,所以和钛合金的弹性模量不具有明显的相关性。
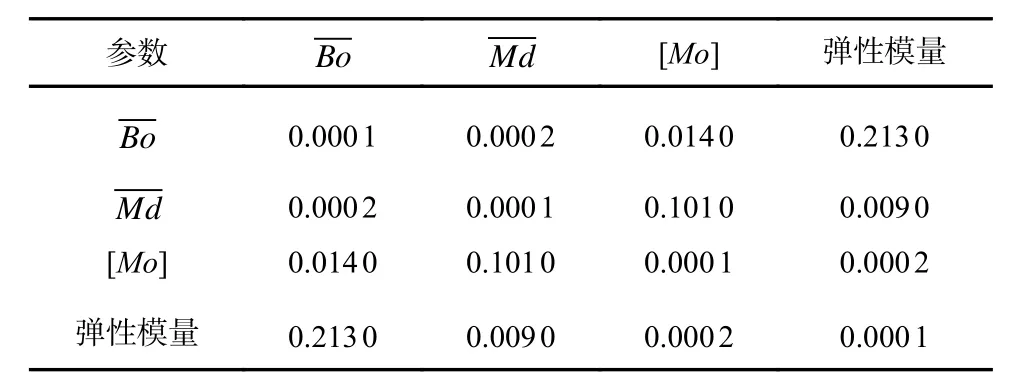
表1 数据集参数之间的P 值Tab.1 P-values between the parameters in the dataset
Bo、Md、[Mo]三者之间的P值<0.05,所以它们之间具有显著的相关性,这说明对于钛合金的弹性模量的影响是间接的。
2.3 模型比较
三种模型经过计算和迭代后,最终确定MLP 结构为3-8-10-1,因此模型的输入节点为3,隐藏层第一层节点数为8,隐藏层第二层节点数为10,最后输出层的节点为1;CNN 模型采用10 个3×3 的卷积核,全连接层节点数为128;RFR 模型的决策树数量为120。
图6 是训练好的MLP、CNN、RFR 模型对验证集数据进行验证所得预测对比图。图6 中红色点线为验证集中钛合金所对应的实测弹性模量,而蓝色则是模型通过大量训练以后预测所得到的相应合金的弹性模量,可以看出,MLP 模型可以很好地去模拟合金的元素配比和弹性模量之间的相应关系,预测值的数据和实测值的数据较为贴合,具有可靠预测合金性能的能力。
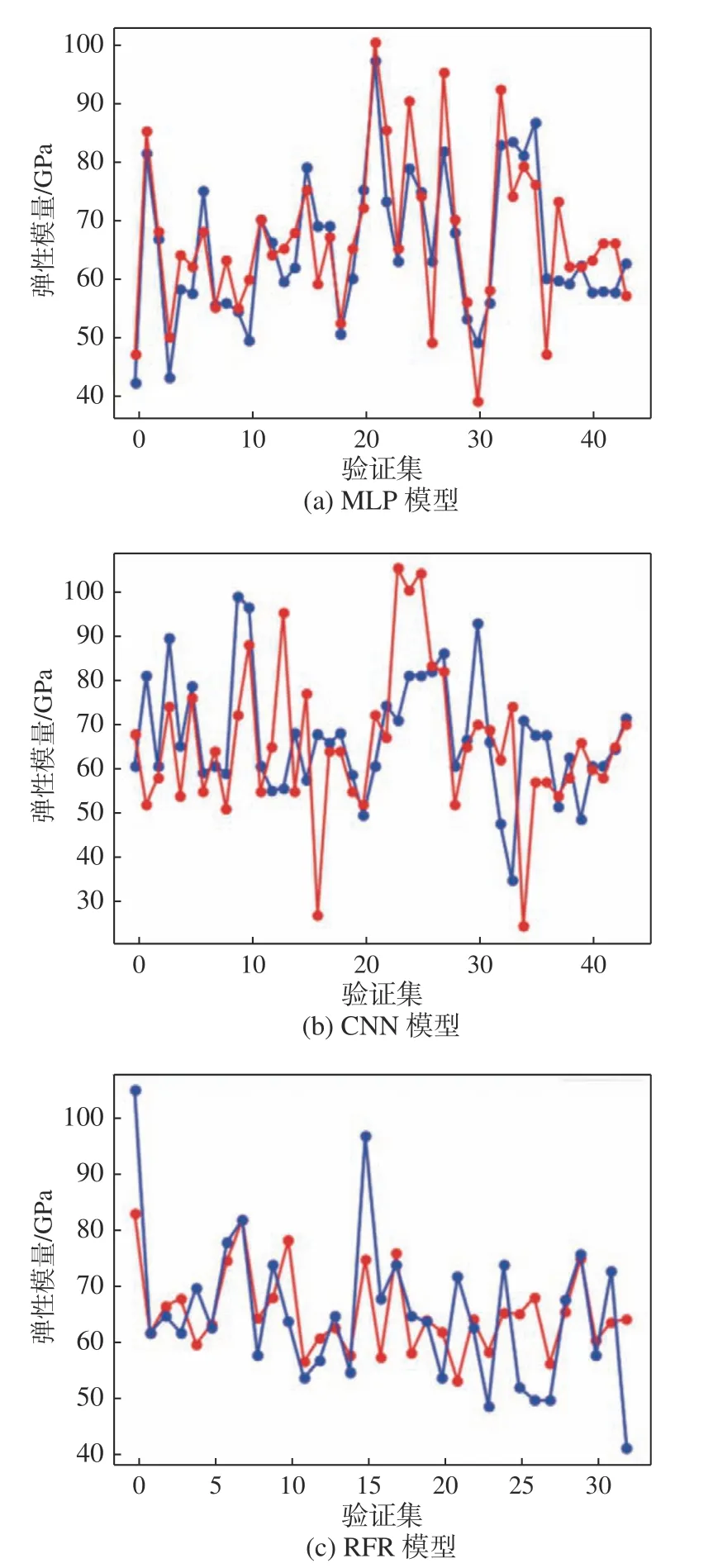
图6 机器学习模型验证集预测图Fig. 6 Prediction images of the validation sets obtained by machine learning models
表2 为预测模型性能指标。从表2 可以看到,MLP 模型的RMSE 和R2 指标平均值分别是7.54 GPa和0.66;CNN 模型的RMSE 和R2 指标平均值分别是3.58 GPa 和-0.61;RFR 模型的RMSE 和R2 指标平均值分别是10.03 GPa 和0.40。当R2 的评分大于0 时才能证明模型的预测结果具有可信度,比较三者R2 评分可知,MLP 模型对于钛合金弹性模量的预测建模是可信度最高的。RMSE 代表预测结果和实际模量之间的偏差,MLP 模型的RMSE 于3 个模型中处于中游。在模型评价中,R2 指标的权重大于RMSE 的,模型的第一评价标准是R2。综合可知,MLP 模型在本文数据集中的预测性能最佳,CNN 模型具有一定的预测能力,但是可靠性不高,RFR 模型的预测能力介于二者之间。MLP 模型综合性能指标相较于其他两个模型更具优势,模型预测结果更为可靠。

表2 预测模型性能指标Tab.2 Performance indicators of the prediction models
为了更加直观地表达MLP 模型在全部数据集上的预测效果,通常采用拟合优度图进行直观判断。图7 是MLP 模型对所有数据集的预测拟合图,图中蓝色圆形点集表示模型在训练集的预测值,红色圆形点集表示模型在测试集上的预测值。从图7 中可以看出,MLP 模型在测试集上的预测值大部分靠近中心线,数据散点分布更紧凑,表明预测值更接近实际值。图7 也反映了MLP 模型对数据集的较好拟合情况。
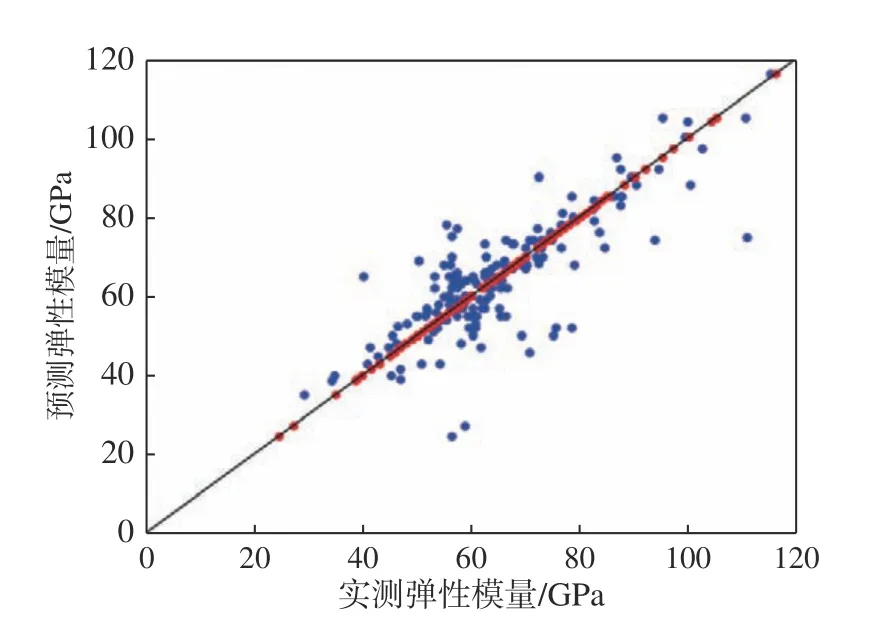
图7 MLP 模型拟合图Fig.7 Fitting graph of the MLP model
2.4 预测结果
为了进一步说明MLP 模型的可靠性,从测试集中选取5 组常见的钛合金进行模型预测分析。表3是5 组常见钛合金的弹性模量实测值与预测值,二者的偏差在MLP 模型的RMSE 范围内,说明预测结果均是合理的,即MLP 模型的预测能力是可靠的。

表3 5 组常见钛合金的弹性模量实测值与预测值Tab.3 Measured and predicted elastic moduli of five groups of common titanium alloys
3 结 论
本文利用合金设计公式转换后的数据集作为原始数据集,建立机器学习模型。通过验证和分析模型的预测性能,得出以下结论:
(1)利用合金设计公式对原始数据集进行转换,解决了原始数据集稀疏值较大的问题。
(2)弹性模量的大小与[Mo]呈显著的正相关,与呈显著的负相关,而与弹性模量之间无显著相关性。通过影响[Mo]、来间接影响钛合金的弹性模量。
(3)建立了基于CNN、REF、MLP 的三种钛合金弹性模量预测模型。其中,MLP 模型对钛合金弹性模量预测的RMSE、R2 指标平均值分别为7.54 GPa、0.66,相较于RFR 模型、CNN 模型,MLP 模型具有更优的预测性能和预测精度。

