S翼型水力优化及非稳态绕流研究

李 忠，马存志，周俊杰，丁 磊

（江苏大学 能源与动力工程学院，江苏镇江 212013）

0 引言

在众多反向对称翼型中，具有极佳绕流性能的S翼型被广泛应用于双向轴流式水力机械［1］，确切的说S翼型作为双向叶轮的设计基元，其水动力特性是影响双向轴流式水力机械能量性能的决定性因素。而S翼型的水力性能与其非稳态绕流特性间存在一定的关联关系，因此为提升S翼型的绕流性能，必须深入探究S翼型非稳态流动特性，揭示诱发S翼型水动力特性恶化的关键因素。

纵观S翼型绕流现状研究，大部分学者基于试验和CFD数值计算开展了S翼型绕流时的气动、水动力特性研究。谢传流［2］对正、负攻角下S翼型的空化特性展开了研究，研究表明在正攻角时S翼型的空泡首先出现在吸力侧，且其冲角越小空化性能越佳。康灿等［3］对不同入流条件下S翼型周围流态展开了研究分析，研究表明S翼型吸力侧的流态随着攻角的增大逐渐失稳，且其尾部的复杂流态受雷诺数的影响较大。李景银等［4］利用试验测得了若干组S形对接机翼的气动特性，研究表明此种机翼的气动性能受尾部形状的关键影响。BALABASKARAN等［5］开展了S翼型的内流试验研究，研究表明S翼型的绕流性能受其最大拱度及厚度的影响。RAMACHANDRAN等［6］利用闭式水洞试验台对不同组合形式的S翼型开展了试验研究，研究指出S翼型的受力特性受攻角的影响较大，应用拱度小于0.05的S翼型可以有效地提升全可逆式潮汐水轮机的性能。MADHUSUDAN等［7］利用可视化试验手段详细探究了S翼型边界层内的流动状态，研究表明S翼型的绕流流场受其型线曲率的影响较大，当翼型壁面为凸曲面时，其对应边界层内的剪切应力最小。综上简述，现有研究关注S翼型水动力特性与几何参数间的关系，并未侧重其水力性能与非稳态流动特性间的内在关系，尤其是缺乏对S翼型非稳态内流特性的试验研究。

本文利用自动寻优流程得到水力性能较优的新翼型，采用数值计算与可视化试验开展了S翼型非稳态流动研究［8］，揭示了S翼型水力性能改善的诱因，为应用于双向轴流式水力机械的S翼型提供设计参考与基础理论。

1 优化设计

1.1 基于CST参数化的S翼型重构

CST参数化方法采用类函数和型函数对翼型轮廓进行精确分析，在翼型优化设计中广泛应用，其数学表达式如下：

式中，C（τ）为类函数；S（τ）为型函数；y为翼型纵坐标；C为翼型弦长；n1，n2为控制系数；Ai为系数因子；Bi（τ）为伯恩斯坦多项式；N为阶数。

为保证翼型前缘型线的曲率连续性，将型函数中的控制系数n1和n2分别取为0.55和1。为保证拟合精度，本文选取N=8，对翼型曲线进行控制，S3525翼型通过CST参数化曲线拟合如图1所示。

图1 S3525的CST拟合效果Fig.1 CST fitting rendering of S3525

1.2 优化方案

以绕流特性较优的S3525翼型作为研究对象，鉴于基础翼型的反向对称结构，其前缘至0.5C范围内的翼型型线决定整体翼型的轮廓特征，因此仅需对0～0.5C范围内的翼型型线进行参数化。

选取攻角、最大厚度及控制翼型形状的系数因子Ai作为自变量，对目标自变量进行适当的范围控制有利于快速寻找到性能优良的参数组合。根据基础翼型的尺寸特征，选定攻角的约束范围为3°～9°。参考轴流泵叶轮设计中翼型截面的最大厚度，将最大厚度的约束范围取为3%～10%。系数因子Ai的约束范围取为-0.1～+0.1。

1.3 优化流程

基于ISIGHT多学科优化平台搭建的自动寻优流程如图2所示。

图2 寻优流程Fig.2 Optimization procedure

其中，DOE为整个优化流程的控制核心，用来提供优化变量、控制自变量的变化范围；MATLAB软件用来实现整个S翼型的外形重构；ICEM和FLUENT软件分别用来划分流域网格和实现绕流域的数值模拟，而CALCULATOR则用来计算所需的优化结果。

优化方法采用Latin Hypercube法，选取升阻比为优化目标，进行500轮单工况优化。从优化结果中筛选出升阻比较高且型线较为光滑的S翼型，标记为OP翼型，与原S3525翼型，标记为OR翼型展开非稳态数值计算及LDA光学试验，就其水力性能的提升诱因进行对比剖析。

图3，4分别示出优化前、后S翼型从前缘至中部的型线和三维模型对比。由图可知，OR翼型的前缘为尖角，而优化后OP翼型的前缘为椭圆角，OP翼型前缘处的拱度及厚度均大于OR翼型。

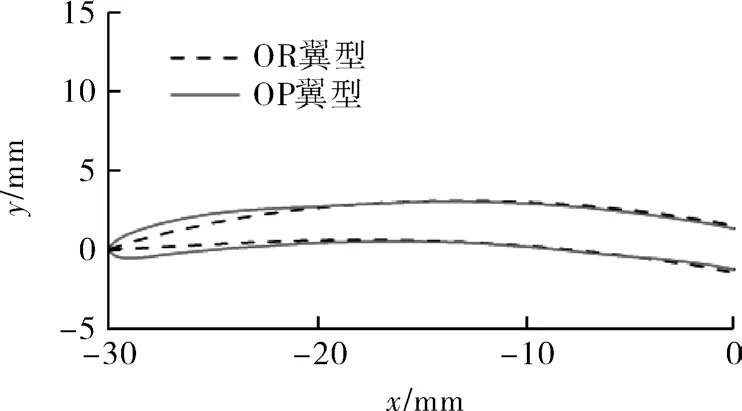
图3 OP与OR翼型分半型线对比Fig.3 Comparison of split-half profiles between OP hydrofoil and OR hydrofoil

图4 OP与OR翼型模型对比Fig.4 Comparison of model between OP hydrofoil and OR hydrofoil

2 试验及数值计算

2.1 试验系统

用于翼型绕流域内单点测速的非接触式光学测试系统的测试域四周均为有机玻璃，以方便LDA激光透射。

2.2 试验模型及测点布置

OP，OR三维试验模型如图5（a）所示，将试验模型布置在如图5（b）所示的矩形可视域中段，其中翼型弦长为60 mm，矩形测试域长为250 mm、高为100 mm、宽为20 mm，通过在其展端固连直径为70 mm的安装圆盘，并在圆盘背部开设定位销孔，利用定位销实现攻角的精准调节。

图5 试验模型及其测试区域Fig.5 Experimental models and testing area

在翼型展向中间截面处按图6所示位置处布置相应的LDA测点，重点探究优化前、后S翼型绕流域及尾迹区内瞬态速度变化规律及其差异。

3 数值计算方法及其验证

3.1 数值计算域

图7示出S翼型的计算域网格划分，计算域大小与试验保持一致，并且在翼型壁面附近的网格采用渐变加密，控制壁面及其附近的Y+值小于1，以满足LES方法对网格的精度要求。

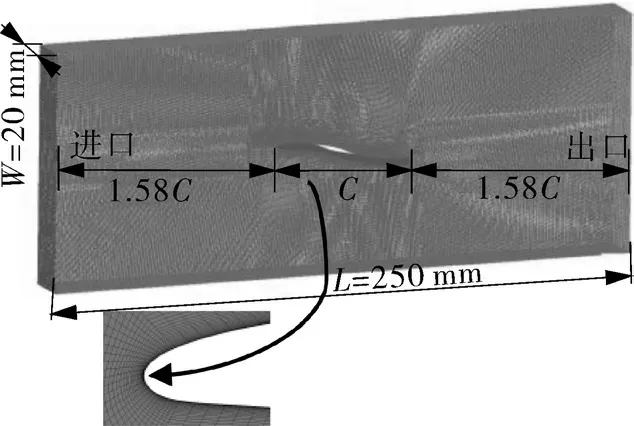
图7 三维计算域及翼型局部网格Fig.7 Three-dimensional computational domain and local grids of hydrofoil

图8示出网格无关性验证。由图可知，当网格数大于171万时，升阻比保持在15.7附近，网格数的提升对升阻比计算精度的提高较小，综合计算资源，最终确定网格总数约为309万。

图8 网格无关性验证Fig.8 Grid independence verification

3.2 计算方法

分别选取速度进口和压力出口作为进、出口边界条件，选用适用于多条件下复杂模型绕流特性预测的K-KL-ω模型，求解方程除梯度以外均采用二阶迎风格式，收敛精度为10-5，速度-压力耦合采用SIMPLE算法。以定常计算结果为基础，利用LES方法开展S翼型非定常数值计算。采用参考文献［9］中确定时间步长的计算方法，其对应的计算式为：

式中，Δt为设定时间步长，s，Δt=0.000 2 s；U∞为来流速度，m/s，U∞=3 m/s；D为弦长。

3.3 计算方法验证

为验证数值计算方法的准确性，结合LES方法和LDA试验在P1监测点的速度频谱展开对比分析，如图9所示。由图可知，两种方法的速度频谱分布特征得到较好的还原，其涡脱频率均为29 Hz左右。

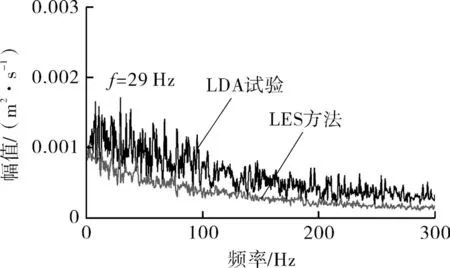
图9 速度频谱对比Fig.9 Comparison of velocity spectrum

引入St数进行量化分析见表2。由表可知，数值计算所得St数略大于试验测得值，但两者的计算结果吻合度极高，对应相对误差不超过3.3%。其中，St数对应的计算式为：

表2 St数对比Tab.2 Comparison of St numbers

综上所述，本文所用数值计算方法准确且可靠，LES方法可准确地捕捉优化前、后S翼型的非稳态绕流信息。

4 水力性能及非稳态绕流特性分析

4.1 翼型性能

图10示出了在不同攻角下OP，OR翼型的升阻比、升力及阻力系数。由图可知，OP翼型的升阻比较OR翼型有大幅的提升，其最大升阻比为29，较原始翼型提升了30%，其对应最优攻角为8°并大于OR翼型对应的6°攻角，同时在对应最优攻角附近OP翼型升阻比下降率明显小于OR翼型，由此表明OP翼型具有更高效的运行范围。由升力、阻力系数变化可知，不同攻角处OP翼型的升力系数大于OR翼型，其平均增值达到0.27，其阻力系数也明显降低。综上所述，升力的可观提升、阻力的大幅降低是优化后OP翼型水力性能提升的主因。

图10 优化前、后翼型的升阻比、升力系数CL及阻力系数CDFig.10 Lift-drag ratio，lift coefficient CL and drag coefficient CD of hydrofoil before and after optimization

4.2 数值计算分析

图11示出了在6°及8°攻角下OP，OR翼型展向中间截面处的Z向涡演化，其中优化前、后S翼型同一攻角处的演化周期基本相同。由图可知，S翼型吸力侧存在较为显著的流动分离现象，并在主流强剪切和逆压梯度的干涉下，分离流无法维持原流态并逐步演化成条带涡，由于受到上述两种干涉能量的持续作用，条带涡的能量进一步耗散并分化成若干圆状破碎涡。相比较而言，压力面处的流态较为稳定，仅在其尾缘处发现流动分离现象，并随时间的演化逐步发展成破碎的涡团。压力侧的正向涡与吸力侧的负向涡随主流向下游发展，形成正、负交替的尾迹涡。

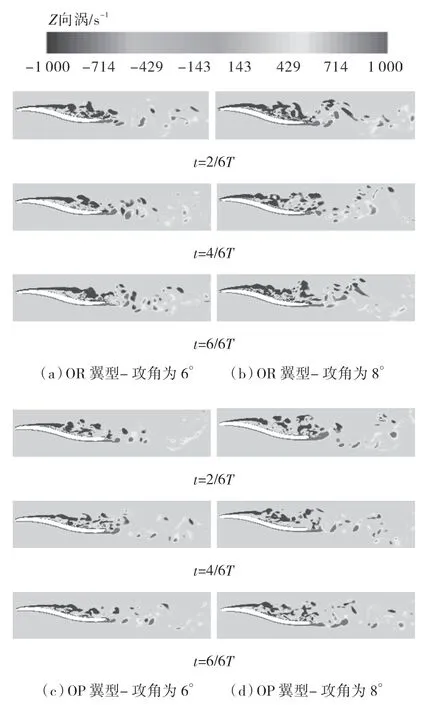
图11 不同攻角下，优化前、后翼展中间截面上Z向涡演化Fig.11 Z-direction vortex evolution on the middle section of the hydrofoil span at different attack angles before and after optimization

对比相同攻角下OP，OR翼型的Z向涡分布可知，OP，OR翼型绕流场中的漩涡演化及分布趋势未有明显差异，但是同一周期内OP翼型吸力侧及尾迹区条带涡的尺度及范围明显小于OR翼型，其吸力面尾缘上方的小尺度涡也逐步消散，且随着攻角的增大该现象愈发显著。上述现象说明OP翼型可以抑制S翼型绕流时产生的大尺度高涡量区，由此预测OP翼型可有效降低非稳态激励源的强度。

图12示出了1个周期内不同攻角下OP，OR翼型表面摩擦系数的变化过程。由图可知，优化前、后S翼型表面摩擦系数从前缘起近乎垂直陡降，再呈小幅陡升，最后沿弦向变化极为缓慢并保持在10量级左右；而从0.45倍弦长起表面摩擦系数逐渐提升。从前缘至0.05倍弦长处，吸力面的表面摩擦系数大于压力面；而从0.05倍弦长至0.1倍弦长处，吸力面及压力面的表面摩擦系数则未有较大差距。

图12 不同攻角下优化前、后S翼型表面摩擦系数Fig.12 Skin friction coefficient on the hydrofoil surface at different attack angles before and after optimization

相比较而言，虽然OP，OR翼型压力面前缘处表面摩擦系数的变化趋势基本一致，但是OP翼型表面摩擦系数明显小于OR翼型；而在吸力面前缘处，OP翼型表面摩擦系数也明显较小且其峰值的降幅大于压力面。从前缘至0.1倍弦长处，OP，OR翼型吸力面处表面摩擦系数的变化呈现差异性，OR翼型的表面摩擦系数先大幅陡降再小幅陡升，最后平缓变化，整个过程呈“L”型，而OP翼型则明显过渡平缓，呈“C”型。同时随着攻角的增大，OP翼型相较于OR翼型其表面摩擦系数的降幅也得到了提升。上述现象表明了OP翼型椭圆型的前缘可以使来流绕S翼型过渡更为合理，有效优化了因液流冲击诱发的不良绕流结构，因而其前缘处的表面摩擦系数得到有效降低，特别是在S翼型吸力面前缘处其绕流状态得到更为显著的改善。

值得注意的是，在攻角为6°下，从OR翼型吸力面0.35倍弦长处起表面摩擦系数出现了明显的波动，而OP翼型不同时刻处对应系数曲线基本吻合，并未呈振荡现象，结合吸力侧的涡量分布可知，OP翼型可以削弱吸力侧涡团的尺度和范围、有效抑制流动分离现象。由此表明，对吸力侧流动结构的优化是OP翼型性能提升的主要原因。

4.3 试验分析

采用湍流强度IT量化S翼型绕流时的速度脉动能量，其计算表达式为：

优化前、后部分监测点处的湍流强度如图13所示。由图可知，S翼型吸力侧的湍流强度沿弦向递减且略大于尾迹区，OP翼型的湍流强度小于OR翼型且其降幅随着攻角的增大而递增，8°攻角下Q2，Q3点的平均降幅可达48%及70%；OP翼型尾迹区部分测点（P1，P11，P12，P5，P51，P52）的湍流也均小于OR翼型，在6°及8°攻角下尾迹近尾缘区（P1，P11，P12）湍流强度的平均降幅皆在36%左右，而P5，P51，P52测点处湍流强度的降幅差异较大，在6°及8°攻角下其降幅分别为8%和17%。由此表明，优化翼型可以削弱尾迹区及吸力侧部分区域的湍流强度，强化了上述区域内的流动稳定性，因而有效优化了非稳态绕流结构。

5 结论

（1）优化后OP翼型的升阻比较OR翼型有大幅的提升，其最大升阻比为29，较原始翼型提升了30%，其对应最优攻角为8°并大于OR翼型对应的6°攻角。

（2）椭圆形S翼型前缘可以降低前缘处的表面摩擦系数，使来流过渡更为合理，有效改善前缘处的不良绕流结构、减少了流动损失。

（3）S翼型吸力侧存在显著的流动分离现象并伴随有周期性涡脱，通过对吸力侧流动分离现象的抑制，可以有效地改善S翼型的非稳态绕流特性，从而实现其水动力特性的提升。