基于WPT 和SSA-BP 的直流充电桩充电模块故障诊断
姚望,张英,王明伟,马永超
(1. 贵州大学电气工程学院,贵阳 550025;2. 贵州电网有限责任公司电力科学研究院,贵阳 550002;3. 清华大学电机系,北京 100084)
0 引言
近年来,新能源汽车的普及推动了充电设施的发展[1]。在碳排放目标以及新基建的激励下,汽车充电设施将会出现新一轮的高速增长[2-4]。其中,直流充电桩具有充电高效、快速等优点,逐渐取代交流充电桩,成为当下热门的研究领域[5]。
充电模块是直流充电桩的核心部件,其主要功能是为电动汽车动力电池充电。充电模块一般由前级和后级两个模块组成[6]。前级模块的作用是将电网输出的交流电转化为稳定的直流电输入到后级,后级模块的作用是将直流电二次转换变换为汽车所需的直流电,具有电压变换和电气隔离的功能。前级结构以三相Vienna整流器为主体来获取稳定直流电,后级结构使用全桥LLC谐振变换器,该结构利用软开关技术可以在极大程度上减小开关损耗,提高系统整体效率[7-8]。
开路故障和短路故障是直流充电桩最为常见的两种故障。短路故障会导致过电流过大,并在短时间内烧毁设备,危害极大。一般在电路中配有熔断装置,保护电路动作将短路转化为开路[9-10]。开路故障虽然不会在一瞬间产生过流,但会导致电网侧电流发生畸变。同时,装置元件应力会因此变大,造成二次故障[11]。因此,对充电模块开路故障的诊断显得十分重要。
目前,对充电模块开路故障的研究仅局限于针对单级结构功率开关开路故障。目前,主流检测手段有两种:电流检测法和电压检测法。文献[12]搭建了充电模块脉宽调制(pulse width modulation,PWM)整流器前级模型,通过仿真得到了频带和频率的故障数据,将这些数据作为特征量进行处理,整理成故障编码的形式,最终实现了对充电模块前级部分的开路故障诊断。文献[13]通过对充电桩前级整流器输出电压进行检测,利用深度神经网络实现充电桩实时故障诊断。文献[14]以V2G充电桩前级结构为研究对象,设置功率开关开路故障仿真模型,分析其电网侧输入电流波形,结合小波包分析法和随机森林算法实现故障诊断。文献[15]建立了两级结构模型,选定电网输入侧电流波形为研究对象,运用电流检测法检测系统运行状态,并且使用传统BP神经网络进行故障诊断。
针对上述分析,本文参考了当下直流充电桩充电模块常用结构,建立了完整的两级结构模型,全面研究了开路故障输出波形特点。同时,选取后级模块输出电压为研究对象,与直流充电桩实际工程应用更契合。本文应用麻雀搜索算法迭代寻优,确定BP 神经网络的全局最优参数,能够改善BP 神经网络的不足,进一步提高模型的诊断率。最后,对本文提出的方法进行仿真分析,以验证所提诊断模型的有效性。
1 充电模块拓扑结构及故障分析
1.1 充电模块拓扑结构
作为直流充电桩最为重要的模块,充电模块主电路一般采用两级变换结构。图1 为本文研究充电模块的前级整流模型,采用三相Vienna 整流器结构,为后级电路提供稳定直流电。
图1 中,ua、ub、uc为三相电网电压,La、Lb、Lc为电感值相等的滤波电感,全控型器件Sa、Sb、Sc和各自并联的4 个二极管组成三相功率开关,Da1、Da2、Db1、Db2、Dc1、Dc2为快速恢复型二极管,C1、C2为直流侧滤波电容。
后级模型采用全桥LLC谐振变换器,能够输出满足汽车需要的直流电,其结构拓扑如图2所示。
图2 中,Q1—Q4是构成逆变电路的4个功率开关管,各自并联一个体二极管和寄生电容。原边谐振回路由谐振电感Lr、励磁电感Lm和谐振电容Cr构成。DR1、DR2、DR3、DR4为输出侧4 个整流二极管,C0和R0分别为滤波电容与输出电阻。
充电模块三相Vienna整流器电路采用单周期控制。单周期控制的优点在于结构简单,能够在一个周期内就实现负反馈控制[16-17]。相比于传统的双闭环控制策略,不仅不需要乘法器,而且无需外加中点平衡电路,能有效解决输出中点电压平衡问题。
本文充电模块后级电路选择电流内环模糊PI控制策略。此控制策略是对传统电压电流双闭环控制的一种优化改进,优点是具有更好的稳定精度和跟随性,克服了传统控制方式下,电压电流突变导致稳定性和跟随性差的问题[18-20]。
1.2 故障分析
前后两级电路所有器件中,电解电容和功率开关故障这两种情况是较为常见且无法避免的[21-23],本文研究重点是电容器件和功率开关的开路故障。由于前后级模块控制电路在整个充电桩系统中起着中枢控制作用,控制着前后级功率开关的导通与关断,其发生故障将导致充电模块功率开关无法正常运作,后果十分严重,因此把此类故障情况也列为研究对象。
由于多个器件同时发生故障的概率较小,本文主要研究单个器件开路的情况,包含正常状态在内共总结出了13种故障类型,故障分类如表1所示。
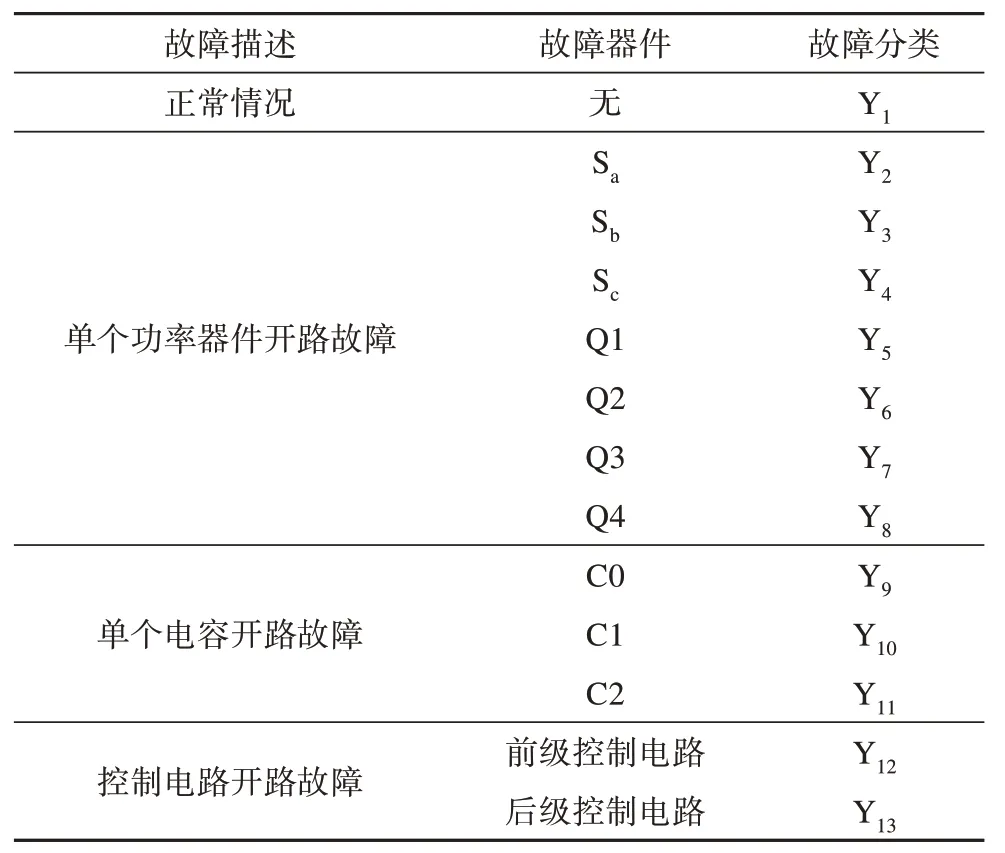
表1 充电模块器件开路故障分类Tab. 1 Classification of open circuit fault of charging module device
2 故障特征提取
2.1 小波包分解
小波包分析在小波分析的基础上进行的扩展,它具有更高的时频分辨率,是挖掘故障特征信号的有效工具[24]。不同类型开路故障的输出电压时域波形中蕴含着频率特征,本文借助小波包分析法对故障输出电压进行小波包分解。由于不同故障类型下各频带能量分布不同,就可以根据频带能量分布的差异,以更直观的形式将频率特征展现出来。图3以3层小波包分解为例进行说明。

图3 三层小波包分解示意图Fig. 3 Diagram of three-layer wavelet packet decomposition
图3 中S(0,0)为原始信号,S(i,j)(i=0,1,2,3;j= 0,1, ···,7)为分解树第i层的第j个节点。初始信号经过三层小波包分解后,表示为:
利用小波包分解得到故障信号特征量,其实现具体步骤如下:1)对采样信号进行小波包分解;2)小波包分解系数重构;3)求取各节点信号能量;4)确定故障特征向量。
利用频带信号能量构造故障特征向量T。
当能量值较大时,为了便于对数据的计算和处理,要对特征向量进行归一化处理。
式中:E(p,j)为p层j节点小波包重构信号能量;E为输出电压第3层小波包分解的频带总能量。
2.2 故障电压特征量提取
本文建立的故障仿真模型输出电压信号特征量提取步骤如下。
1) 搭建故障仿真模型,在不同类型故障下对充电模块输出电压即输出负载两端电压进行采样。根据奈奎斯特采样定律,只有采样频率高于信号最高频率两倍才能确保采样信号完整且不失真[25]。通过对故障信号的频率分析,采样频率设定为1 600 Hz。
2) 经过仿真试验多次对比,选用db3 小波包,对采样信号进行3 层小波包分解,可以得到8 个节点。
3) 重构小波包分解系数,求取不同故障下各频带对应小波包能量值,最后归一化处理得到一组新的故障特征量。
在实际运维检测中,通过检测装置测量到的故障波形往往都是故障发生一段时间后的数据。因此,为了更贴合实际现场检测情况,本文选择故障波形重新稳定后的部分为研究对象。在对原始故障电压信号进行分析后发现,信号中直流分量占据主导,导致小波包分解后的能量谱分布区分度较低。于是,对原始故障信号进行预处理,剔除直流分量后,再进行小波包分解。由于有些故障类型能量谱分布较相似,导致后续故障诊断区分度较低。通过对输出电压波形分析,不同故障类型的输出电压直流分量幅值存在较大差异,即可以将直流分量也看作一个特征量和处理后新的能量谱特征向量作为新的故障特征量。本文的最终确定的故障特征向量:T=[Ud,E0,E1,E2,E3,E4,E5,E6,E7]。式中:Ud为直流分量;E0—E7为归一化后的能量谱值。
3 麻雀搜索算法(SSA)优化BP神经网络
3.1 BP神经网络
BP 神经网络一般由多层组成,典型的三层BP神经网络模型,由输入层、隐含层和输出层构成。
如图4 所示,在BP 神经网络中,输入量沿着正向传播,由输入层到输出层。BP 神经网络在训练后具有储存历史故障信息的能力,可以运用BP神经网络进行故障诊断。对已有数据信息进行网络训练,将当前数据和历史信息数据比较,从而确定故障类型。本文利用BP 神经网络,将提取的特征量和故障类型实现对应,进行故障诊断。但是传统BP 神经网络存在一定局限性,例如对初始权重敏感,由于传统神经网络在训练过程中会给定一个随机初始权重,导致BP 神经网络往往不可重现。另外,容易陷入局部最优或训练速度过慢也是其存在的不足。在实际应用中,往往采用优化后的BP算法。
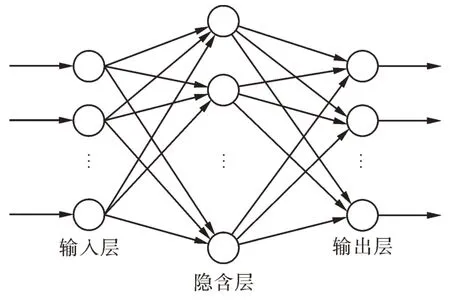
图4 BP神经网络结构Fig. 4 BP neural network structure
3.2 麻雀搜索算法(SSA)
麻雀搜索算法(sparrow search algorithm,SSA)是受麻雀的捕食行为和警戒行为的启发而提出的一种群智能优化算法[26]。
在麻雀群体中,一般有两种不同类型的麻雀,一种是发现者,另一种是加入者。其中,有大约10%~20%数量的麻雀负责侦察预警,称之为警戒者。发现者给加入者提供捕食的区域和方向,加入者通过发现者来获取食物。一旦麻雀发现捕食者,就会发出预警信号,当预警值大于安全值,发现者就会将加入者带到别处安全区域寻找食物。麻雀搜索算法的数学模型就是根据麻雀的这类行为提出的。
根据以上描述,将麻雀的行为理想化,可总结出数学模型如下。
发现者具有较高的能量,有更好的个体适应度,发现者位置按式(4)进行更新。
式中:t为迭代次数;G为最大迭代次数;Xi,d为第i个麻雀在第d维中的位置;α为(0,1]间的一个随机数;R2为预警值,是一个位于(0,1)的随机数;S为安全值,取值范围为[0.5,1];Q1为一个随机数,按正态分布;L为1×d的矩阵。
对于加入者来说,当它们察觉发现者寻觅到好的食物,会立刻去抢夺。如果抢夺成功,就会获得发现者的食物。要是自身能量较低,它们会去其他地方去寻求更多能量。加入者位置更新如式(5)所示。
式中:为当前找到最佳食物源的发现者所处位置;为全局最差位置;Q为一个服从高斯分布的随机数;A为1×d的矩阵,矩阵中每个元素为1或-1,且A+=AT(AAT)-1;当i>n/2 时,说明第i个加入者适应度低,没有获取到食物,需要飞往其他地方获取能量。
警戒者位置更新如式(6)所示。
式中:β为全局最优位置,是一个服从高斯分布的随机数;K为取值范围在[-1,1]的随机数,为防止分母为0,设置一个较小常数ε;fi为第i个加入者适应度值;fg、fw分别为整体最佳和最差适应度值;为全局最佳位置。
3.3 SSA优化BP神经网络
选择合理的权值和阈值将会有效提高BP 神经网络的诊断效果。本文利用SSA 算法良好的全局搜索能力,优化BP 神经网络的初始权值和阈值,改善BP 网络性能。图5 为SSA 优化BP 神经网络流程图,算法优化步骤如下。

图5 SSA优化BP神经网络流程图Fig. 5 Flow chart of SSA optimized BP neural network
1) 数据归一化预处理。将样本数据归一化,解决奇异样本导致神经网络收敛慢、训练时间长的问题。
2) 确定BP 神经网络结构。本文设置了9 个故障特征量,输入神经元数量为9。输出变量为故障类型即故障1,2,…,13 为单输出,所以输出神经元数量为1。通过反复实验比较,选定隐含层神经元数量为12 时诊断效果最佳,因此BP 神经网络结构为9-12-1。
3) 初始化SSA 参数。初始化SSA 算法相关参数,包括种群规模、最大迭代次数、预警值、发现者和加入者比例等。
4) 确定适应度函数,计算初始适应度值。先对BP 神经网络进行初次训练,将训练集预测误差和测试集预测误差的和作为适应度函数,适应度值越小,表明误差越小。确定当局最优的适应值和对应的位置。
5) 更新麻雀的位置。判断预警值和安全值的大小,更新发现者的位置。加入者的位置根据它们自身的适应度在不断变化。警戒者的初始位置是随机产生的,根据麻雀个体的适应度值和当局最优适应度值的比较,不断更新警戒者的位置。
6) 计算麻雀位置更新后的新适应度值并与之前最优适应度值相比较,更新全局最优信息。
7) 判断迭代次数是否满足预定值。若不满足,返回继续迭代。反之则停止迭代,得到网络最优权值和阈值,生成最优的BP网络模型。
4 仿真结果及分析
本文利用MATLAB/Simulink 搭建直流充电桩充电模块仿真模型,前后级主电路设计如图1—2所示,关键参数设计如表2 所示。整个充电模块输入相电压为220 V,额定输出电压为750 V,输出电流为20 A,输出额定功率为15 kW。交流侧前级整流电路输入滤波电感具有能量储存和滤波作用,考虑到跟踪输入电压能力和电流纹波,电感取值为4 mH,直流输出侧电容为2 500 μF。全桥LLC 谐振变换器谐振器件Lm、Lr和Cr的参数值分别为95.8 μH、23.95 μH 和105.78 nF,输出滤波电容容值为1 500 μF。为使仿真更接近实际情况,仿真实验均考虑到功率开关的导通电阻等因素。

表2 充电模块主电路设计参数Tab. 2 Design parameters of main circuit of charging module
在进行故障仿真时,故障设定在1 s 处,仿真总时长为8 s。图6为充电模块正常工作时和发生故障状态下输出电压波形(同一种故障类型波形相似,基本重叠)。从图6 中可以看出,故障波形在6.5 s后趋于平稳。同一种故障类型时域波形差别不大,前级单个功率开关开路故障波形和正常波形在平稳区段有部分重叠。本文所研究的故障类型均表现为对输出电压产生不同程度的畸变,所以单从波形图分析,并不能准确区分故障类型,需借助小波包分解技术提取有效特征量。
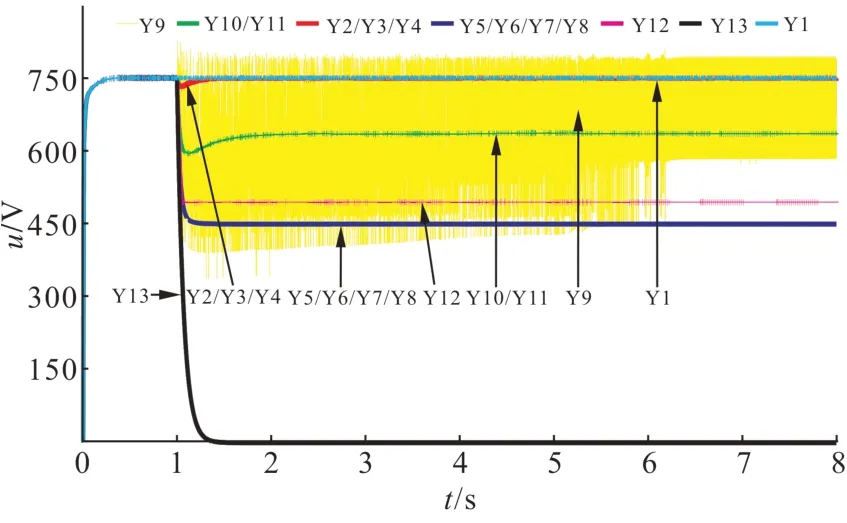
图6 故障状态输出电压波形图Fig. 6 Fault state output voltage waveform
图7 为滤波电容C0、前级功率开关Sa、后级功率开关Q1 开路故障下输出电压能量频带能量分布对比图。可以看出,无故障状态和故障状态下的输出电压频带能量值分布明显不同,即使同种类故障,频带分布也有差异。综上所述,每个频带对应的能量值就可以被看作是一个充电模块故障特征向量。

图7 小波包能量谱图Fig. 7 Wavelet packet energy spectrum
本文采集样本数据时,分别考虑额定负载、0.8 倍欠载和1.2 倍过载情况,每种负载下均考虑到输出滤波电容的容值波动,最终确定了50 种工况。样本总数13×50=650 组数据,将650 组数据分为两部分,455 组数据当作训练集,195 组数据当作测试集。将数据带入9-12-1 结构的BP 神经网络中,利用SSA 算法优化BP 网络权值和阈值。不断迭代计算适应度值,麻雀个体的适应度变化如图8所示。
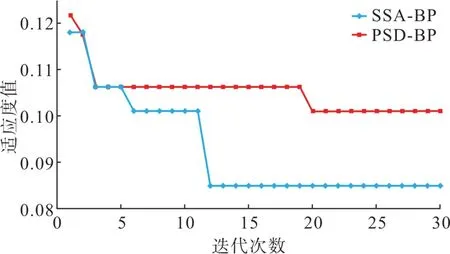
图8 算法适度曲线Fig. 8 Algorithm fitness curves

图9 算法预测结果对比Fig. 9 Comparison of algorithms prediction results
从适应度函数曲线可以看出,通过不断迭代更新麻雀的位置,整体误差不断下降,得到最优解即为BP神经网络的最优权值和阈值。
为了验证所提出方法的优越性,本文分别采用传统BP、PSO-BP 和SSA-BP 这3 种方法对455 组训练样本进行训练。为了保证对比结果的有效性,3种方法采用相同的BP 网络参数:最大迭代次数1 000,学习率0.01,训练目标误差1 × 10-3,激活函数选用logsig。其中,PSO-BP 算法[27-28]和SSABP 算法的参数见表3。195 组测试集的分类结果表明,经过SSA 优化后的神经网络迭代和收敛速度更快,均方误差更小,故障分类的准确率有所提高,结果如图8—9和表4所示。

表3 算法参数设置Tab. 3 Algorithms parameters setting

表4 算法结果比较Tab. 4 Comparison of algorithm results
5 结语
本文针对直流充电桩的充电模块进行了深入的研究,分析了充电模块的工作原理和故障类型;搭建了仿真模型,并利用小波包分解,提取输出电压的有效故障特征向量作为故障诊断的依据,实现故障定位。针对传统故障诊断方法的不足以及传统BP 神经网络存在的局限性,本文提出了一种基于SSA-BP 的充电模块故障诊断方法。利用SSA 算法较好的全局搜索能力优化BP 神经网络初始权值和阈值,以提高故障诊断率。通过仿真实验验证,SSA-BP 算法故障分类准确率达到93.85%,同条件下比传统BP和POS-BP诊断模型分别提高了7.70%和4.62%,故障诊断率满足要求,表明了本文所提诊断方法对直流充电桩故障诊断有一定的现实指导意义。

