考虑负荷重要程度含DG 中压配电网电压调控策略

欧阳森，于业辉，张真

（1. 华南理工大学电力学院，广州 510640；2. 国网浙江省电力有限公司嘉兴供电公司，浙江 嘉兴 314033）

0 引言

随着光伏电源在电力系统中渗透率不断提高，光伏电源并网容量和数量不断增加，光伏发电产生的剩余能量馈入电网导致线路中潮流双向流动，同时光伏出力具有随机性，导致各负荷的节点电压各时段波动较大，合理地调控配电网母线的电压对改善用户的电压质量具有重要意义［1-5］。

各负荷的重要程度对电压调控具有重要的指导意义。文献［6］建立负荷重要程度指标体系指导可靠性评估，确保重要负荷优先供电，可将该思路引入电压调控策略中。文献［7］的传统电压调控策略仅考虑了母线电压合格率，无法针对负荷重要程度不同提供最优的调控方案，存在一定的盲目性。总之，用户负荷对用电电压的需求不同［8］，对电网电压调控策略有较大的影响，因此考虑负荷重要程度对电压调控具有的重要指导价值。文献［9］采用一种改进层次分析法（analytic hierarchy process，AHP），通过构造最优传递矩阵简化一致性检验，并以五标度法构建判断矩阵简化了计算。客观评价方面传统熵权法［10］忽略了指标数据相关性和冲突性带来的价值信息，对客观数据的利用不够全面。同时现有评估模型缺乏对主、客观两方面价值信息的有效融合，无法有效反映指标劣化程度，进而辨别负荷节点电压调控的需求程度。

目前，针对中压配电网电压调控的相关研究较多［11-12］，但讨论在高渗透光伏下，从源-网-荷三方面组合变权法评价用户负荷重要程度并指导电压调控的文献较少。文献［13］分析在无功补偿资源匮乏下，提出中压母线电压质量调控及评价方法，但该方法无法适用于涉及高渗透光伏入网导致电压剧烈波动的场景。文献［14-15］均考虑了接入大量光伏引起逆向潮流导致电压越限，但是未能区分电压正越限与负越限两种情况的调控侧重点以及各节点负荷的重要程度。文献［16］结合含分布式电源的电压调控现状，归纳了现有研究方法。文献［17］分析了电压抬升现象产生的原因，提出了一种有功无功协调控制策略。文献［18］讨论诸多限制因素对并网点电压的影响，并对比分析不同电压质量补偿方案。现有调控策略仅保证电压不越限，未区分调控的重点以尽可能地满足用户的需求。综上所示，现有电压调控策略缺乏对负荷重要程度的考虑；同时无法有效解决高渗透光伏接入后电压双向越限和剧烈波动的问题，调控策略具有盲目性。

因此，本文提出一种考虑负荷重要程度和高渗透率光伏接入的中压配电网电压调控策略。从用电用户和供电部分两个角度分析负荷重要程度指标，采用改进层次分析法和改进指标相关性权重法（criteria importance through intercriteria correlation，CRITIC）综合权重，并利用劣化度构造变权函数修正综合权重，依据用户的评估值确定用户负荷重要程度系数；依据调控前后负荷的电压正负偏差和电压波动的改善大小，结合负荷重要程度系数建立调控效益模型，并以调控效益最大为目标，针对光伏逆变器的可调无功容量、有载调压变压器分接头以及电容器投切组数进行优化，求解多场景和多时段下配电网最优电压调控方案，通过改进的高渗透率光伏下的IEEE 33节点系统验证方法的有效性。

1 负荷重要程度评估指标

高渗透率光伏下中压母线上的用户电压存在双向偏差，电压调控不可能同时改善所有用户电压质量，而现有调控策略缺乏对部分重要用户的针对性。因此本文引入负荷重要程度指导各用户电压调控，用以区别用户负荷的差异性是有必要的。考虑从源-网-荷三方面分析负荷的重要程度，在电源侧DG 出力波动率以及电压越限会限制其并网功率，若该负荷点能够得到重视，可通过电压调控提高DG 消纳率，发挥其潜在价值；在电网侧除了需要考虑传统电压偏差指标之外，还需分析在高渗透率光伏下的电压波动、三相不平衡等电压质量指标；在负荷侧社会效益决定供电部门对用户负荷的重视程度，社会效益包括用户用电量以及用户用电满意度，此外还需考虑用户的负荷等级，等级越高调控所带来的效益则越高。综上所述，本文考虑选取新能源效益、电压质量、负荷社会效益3 个一级指标。

1.1 新能源效益指标

接入高渗透率光伏的中压配电网因光伏出力的随机性导致节点电压越限，进而限制并网容量、消纳率。因此电源侧考虑DG的弃光率和渗透率。

弃光率越高代表该负荷点光伏出力受电压约束越严重，电压调控能够提高消纳率的空间越大，因更加重视该负荷点的电压调控，计算公式如式（1）所示：

式中：ξpvi为第i个光伏电站的弃光率；T为统计周期；为tk时段的并网功率；为统计周期内光伏电站实际可发出的总功率。

渗透率反映负荷点接入光伏电量的大小，渗透率越高代表该负荷点向电网输送功率越高，火电厂的耗煤量降低，经济效益越高，因此电压调控时更加重视这些节点的电压改善程度，计算如式（2）所示：

式中：γpvi为第i个光伏电站的渗透率；PG，tk为tk时段发电厂发出的有功功率之和。

1.2 电压质量指标

高渗透率光伏接入中压配电网会对电压质量的谐波含量、三相电压不平衡度、电压波动等产生较大影响。其中，对配电网电压质量中的电压偏差、电压波动影响尤为突出。当配电网接入光伏后，使沿馈线各负荷节点处的电压被抬高甚至越限，影响用户的供电质量和安全性；光伏发电输出功率具有随机性，使得系统电压整体波动较大。综上本文选取电压偏差、电压波动、三相不平衡和谐波电压畸变率作为电压质量评估指标的二级指标。

1） 电压偏差指标。

文献［19］规定10 kV 及以下三相供电电压的电压偏差限值为在标称电压±7%以内，而电压偏差在±3%以内时，电压的分布特性最优，则负荷点j的电压偏差水平可由式（3）计算求得：

式中：ξj，tk为负荷点j在tk时段的电压偏差；Uj，tk为负荷点j在tk时段的电压值；UN为系统标称电压。

2） 电压波动指标。

电压波动指标反映光伏随机波动导致整个周期内各时段变化的电压幅值波动，采用相邻两个时刻电压的标准差与采样周期内电压监测值的均值之比反映节点的电压波动水平，如式（4）所示。

式中：ɛj为负荷点j的电压波动值；为负荷j点在检测周期内的电压均值。

3） 谐波电压畸变率指标。

光伏并网逆变器的大量引入使得系统谐波含量显著增加，负荷点谐波含量越高，该负荷点越需要得到改善。

式中：THDj，tk为负荷点j在tk时段的谐波电压畸变率；Uj，tk，h、Uj，tk，1分别为tk时段负荷点j的基波电压和h次谐波电压值。

4） 三相不平衡度指标。

单相光伏及负荷的接入使得系统三相电压不对称，影响系统安全稳定运行。

式中：βj，tk为负荷点j在tk时段的三相不平衡度；、分别为tk时段负荷点j的正序分量均方根值和负序分量均方根值。

1.3 用电负荷效益指标

电压调控也应注重用户负荷侧的需求，一方面不同等级负荷的电压需求不同，负荷等级越高时对电压调控的需求越高，另一方面为反应用户侧的用电服务及管理水平，需获取用户用电意见，反馈电压调控的效果，引入用户满意度指标，通过电力用户的评价意见为电压调控提供指导价值。此外用户用电量直接决定供电部门对不同负荷点的重视程度。因此负荷侧考虑采用负荷等级、用户满意度以及用户用电量3个指标。

电力负荷依据文献［20］可分为3 个等级，不同等级负荷对社会产生的效益不同，因此不同等级负荷的重要程度不同，可采用不同分值进行定性量化。用户满意度指标可通过设计调查问卷对周期内用电体验进行评估，求取各负荷点的平均得分。用电量指标指在检测周期内各负荷点的用电总量，单位为kWh。

1.4 负荷重要程度指标体系

从源-网-荷三方面分析电压调控时各负荷节点的重要性，负荷点越重要电压调控后所取得的效益越高，从新能源效益、电压质量、用电负荷效益3个方面建立负荷重要程度指标体系，如图1所示。

图1 负荷重要程度评价指标体系Fig. 1 Evaluation index system of load importance

图2 考虑负荷重要程度的配电网电压调控优化流程图Fig. 2 Flow chart of distribution network voltage regulation optimization considering load importance

2 负荷重要程度评估方法

2.1 改进AHP确定主观权重

由于传统层次分析法通过九标度法建立判断矩阵常出现数据繁杂、容易出现严重不一致性的问题，且需要经过多次调整才能一致性检验合格，计算繁琐。因此本文使用三标度法构建判断矩阵，再由最优矩阵导出拟优一致矩阵，直接求出权重，使其自动满足一致性条件，从而不需要一致性检验［21］。计算步骤如下。

1） 综合R位专家意见比较G(i)与G(j)的重要程度对指标打分，构建比较矩阵A为：

式中：aij为比较矩阵元素；G（i）为第i个指标的重要程度。

依据比较矩阵元素计算判断矩阵元素为：

式中：cij为判断矩阵元素；ri为矩阵A第i行的对角元素与上三角元素之和；rmax和rmin分别为ri中的最大与最小元素；n为指标数量。

进一步通过判断矩阵计算拟优一致矩阵D：

式中dij为第i、j项指标相对重要程度之比的修正值。

计算第α位专家所确定的矩阵D的特征向量qα，然后求解专家组确定的主观权重为：

式中：为第j项指标的主观权重；为第α位专家所确定第j项指标的主观权重；R为专家人数。

2.2 改进CRITIC法确定客观权重

CRITIC 法相比较于传统客观赋权法不仅考虑了指标所含信息量的大小，还充分计及了不同方案间的对比和评估指标间的冲突性。鉴于电网侧电能质量各指标间具有较强的相关性，用户负荷效益指标具有较强的离散性，本文对CRITIC 法［22-23］做如下改进：考虑引入相关系数描述指标间对比强度；修正原相关系数为绝对值描述指标间冲突程度；采用冗余信息熵描述指标间离散程度。计算模型如下：

式中：j，j'= 1，2，…，n；j≠j'；为指标Pj由改进 CRITIC 所确定的客观权重；m为指标个数；Mj为指标Pj所含信息量，且Mj越大，Pj所具有的信息量越大，Pj越重要；rj、rj'分别为指标Pj和Pj'的变异系数；为指标Pj的归一化指标值均值；ρjj'为指标Pj和Pj'的相关系数；cov(pj，pj')为标准矩阵中第j列和第j'列的协方差；pij为对象Oi的指标Pj的归一化指标值；Ej为指标Pj的冗余信息熵；bij为归一化值。

2.3 负荷重要程度综合评估

依据改进AHP 和改进CRITIC 法得到的主观、客观权重采用最小鉴别信息原理求解组合权重wi，为增强不同需求场景下对恶劣指标的反应灵敏度，本文引入变权函数φi(x)修正组合综合权重为变权计算模型如下：

式中：ω'=[ω'1，…，ω'n]T为指标的变权权重向量；φi(·)为第i项指标变权函数；μi为第i项指标的劣化度，本文采用梯形函数确定劣化模型［24］。

式中：δi为第i项指标的状态值；δ0i为指标正常范围的边界；劣化度μi∈[0.01，1]，其值越小表征指标的劣化程度越高。

本文依据双激励线的原理构造三段式的惩罚和激励变权函数：

式中：β为变权系数；本文β取0.1表征弱强度的奖惩力度；当劣化度低于0.75时，采用较重的惩罚力度；当劣化度高于0.9 时，采用较轻的激励力度；若劣化度在（0.75，0.9］范围内则不惩罚也不激励。

则评估对象Si的综合评价值为yi：

式中bij为第i个评估对象第j项指标的归一化值。

依据评价值计算方法可知：综合评价值越大，即代表该负荷节点的相对重要程度越高，在电压调控过程中更应注重该类点电压改善程度。依据负荷点的评估值设定各点的重要程度系数如表1所示。

表1 负荷点评估值及负荷重要系数Tab. 1 Load point evaluation value and load importance coefficients

3 考虑负荷重要程度的电压调控优化模型

在面向高渗透率光伏接入后，传统电压质量仅用电压合格率，已难以体现波动性电压及双向越限对配电网造成的影响。因此根据电压质量评估结果动态调控各节点电压以获取最大效益更有研究价值。本文提出一种考虑负荷重要程度和高渗透率DG 的电压调控优化模型，为衡量电压调控策略的优劣性，设各负荷点电压偏差和电压波动调控效益分值如表2所示。

表2 电压偏差及电压波动调控分值Tab. 2 Voltage deviation and voltage fluctuation control score

3.1 目标函数

在一个完整调度周期（24 h）内，通过优化每一个时段内DG 的时序无功功率出力、变压器抽头档位以及电容器组数使得系统节点电压质量得到最大改善，本文将电压双向越限和电压波动改善分值加权求和，并乘以负荷点重要程度系数作为调控效益，目标函数如式（16）所示：

式中：Fsys（tk）为tk时段的系统电压调控效益值；λi为第i个用户负荷的重要程度系数；fi（tk）为tk时段第i个用户负荷的电压偏差调控分值；gi（tk）为tk时段第i个用户负荷的电压波动调控分值；ξ为电压正负偏差的比例系数；本文取ξ=0.5。

3.2 约束条件

为保证高渗透光伏下配电网能够安全稳定的运行，本文建立以下约束条件：系统安全运行约束、交流潮流功率约束、DG 运行约束、变压器和电容器组运行约束。

1） 系统安全运行约束

式中：Umin、Umax分别为节点电压最小、最大允许值；Imax为支路电流最大允许值；ui为节点i各时段电压幅值的平方；lij为支路ij电流幅值的平方。

2） 交流潮流功率约束

式中：Ptk，ij、Qtk，ij、Itk，ij分别为tk时段交流系统中注入支路ij的有功功率、无功功率、电流幅值；Rij、Xij分别为支路ij的电阻和电抗；Ωb为节点集合。

3） DG出力约束

式中：、分别为tk时段节点i处DG 实际发出的有功功率和无功功率；为DG 的额定容量；λmax系统最大允许DG 渗透率；Ptk，E为tk时段系统额定功率；、分别为tk时段节点i处DG允许最大和最小无功出力。

4） 变压器与电容器组运行约束

式中：为tk时段与节点i相连的可调变压器档位；vtk为档位数；nD为最大可调档位数；Dmin相邻两个档位之间的距离；为tk时段节点i处投入的电容器组数；、分别为节点i处电容器组最大和最小允许投入组数。

针对传统遗传算法（genetic algorithm， GA）采用固定的交叉与变异概率导致前期全局搜索能力不足，后期已陷入局部最优的缺陷［25］。本文考虑迭代初期设置较大交叉概率以增强全局搜索能力，后期又稳定于一个较小值以保证优秀个体不被破坏，依据指数模型构造交叉概率随进化代数增大而递减趋势如式（24）所示，且最终稳定于预设较小值Pc.min。为抑制算法早熟，本文赋予适应值较优的个体较小的变异概率，适应值较差的劣质个体则赋予较大的变异概率，利用适应度值与当前种群最优值差值率调整变异概率，以提高算法的收敛速度，变异模型如式（25）所示。

式中：mtmp为一个中间计算变量；TGen为预设的最大进化代数；t为当前进化代数；Pc.min与Pc.max分别为预设置的最小与最大交叉概率；Pc（t）为当前第t代种群的交叉概率：Pm.max与Pm.min分别为预设置的最大、最小变异概率；f（Xi）为个体Xi的适应值；fmax与fmin分别为种群的最大与最小适应值；Pm（t）为第t代种群中个体Xi的变异概率。

3.3 考虑负荷重要程度配电网电压调控优化流程

本文考虑负荷重要程度和高渗透光伏接入对系统电压调控的影响，建立中压配电网电压调控优化模型。首先从新能源效益、电压质量以及用电负荷效益三方面建立中压配电网负荷重要指标体系；采用改进AHP 和改进CRITIC 法求解指标权重，采用指标劣化度实现综合权重变权，进而确定各用户负荷点重要程度系数；然后，建立以系统各负荷点电压调控效益最大为目标的系统电压调控优化模型；采用改进遗传算法对电压调控模型进行求解，从而确定各时段DG 时序无功出力、变压器抽头档位以及电容器组投入组数。配电网电压调控优化流程图如2所示。

4 算例分析

高渗透率光伏下的改进IEEE 33 节点系统拓扑结构如图3 所示，节点18、33、22、11、26 分别接入额定容量为0.9 MVA、0.6 MVA、0.1 MVA、0.1 MVA、0.4 MVA 的光伏组件，无功调节范围设为有功功率的±20%，且可作为无功支撑。在节点6、13、29 分别装设6、8、6 组并联电容器，每组电容器容量为25 kvar。本文依据不同的光伏出力曲线进行场景划分为3 种场景。采用改进GA 进行求解，使用MATLAB R2018 a进行编程，种群个数为100，最大迭代次数为100 次，交叉概率范围为［0.7 0.9］，变异概率为［0.05 0.2］。

图3 高渗透率光伏下的改进IEEE 33节点系统Fig. 3 Improved IEEE 33-node system under high permeability photovoltaic

4.1 负荷重要程度评价结果

为对比分析改进前后评估方法的优势，各用户重要程度指标的权重计算结果如表3 所示。通过AHP 与IAHP 所得主观权重变化一致，指标P21 权重最高，P24 权重最低，但IAHP 将一致性检验步骤改进为构造一致性矩阵，省略了一致性检验可能造成的繁琐计算。传统的熵权法因弃光率和渗透率指标差异小且指标值的熵值接近1 的较多，导致P11 与P12 权重过大，所得综合权重因此不合理；改进CRITIC 法可有效避免指标值微小变化引起权重大幅变化，而导致赋权结果不理想的情况，同时也拉开各指标之间差距，通过劣化度计算变权函数修正综合权重实现变权，劣化度高指标赋予较大权重，劣化度低指标赋予较小权重。

表3 负荷重要程度指标权重Tab. 3 Load importance index weight

对比分析各用户的重要程度评估值以及重要程度系数如图4 所示，传统方法与改进方法均判断出负荷节点18、28、33 对于电压调控的重要程度较高。但传统方法计算的评估值差异较小，导致无法拉开负荷重要程度系数的差距，失去重要程度评估的意义。而改进评估方法计算的评估值区分度较大，同时可有效突出重要负荷节点并赋予其较高的系数，为后续电压调控提供指导。

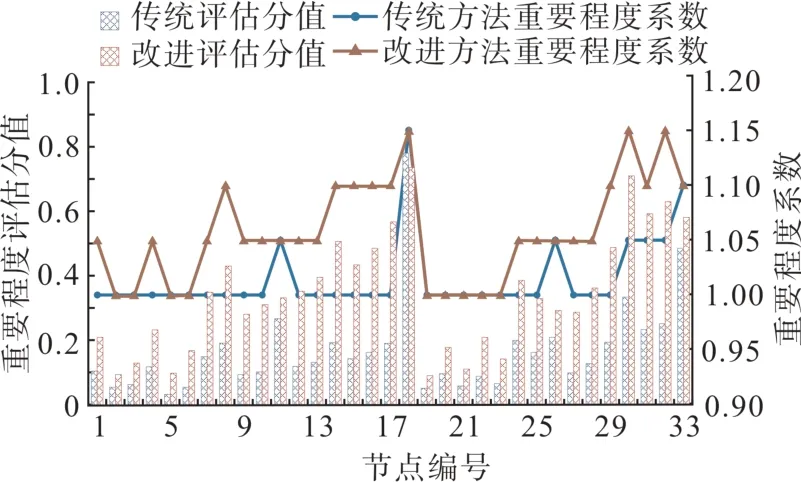
图4 评估结果及重要程度系数对比Fig. 4 Comparison of evaluation results and importance coefficient

4.2 电压调控策略优化结果

4.2.1 云朵效应场景下电压调控策略结果

选取云朵效应场景下采用本文改进赋权方法确定负荷重要程度，求解各时段内变压器分接头档位、并联电容器投入组数以及光伏组件无功出力情况结果如图5 所示。在云朵效应场景下，时段10—12 和16—18 光伏系数骤降，此时光伏组件有功出力减小，电压下降且电压剧烈波动。为降低电压偏差和减小电压波动，电压调控采取调整抽头位置，图5（a）中10—12、16—24 抽头处于5%位置；同时增加并联电容器投入组数，图5（b）中10—12 和16—18 时段内电容器组数显著增加，20—22 时段内数量增加是由于该时段内出现负荷高峰，并且夜间无光伏有功功率出力，为提高电压需投入较多电容器组数；最后调节光伏逆变器无功功率出力，同理在上述时段内无功功率出力显著增加，在1—8 以及22—24 时段内吸收无功功率是由于负荷较轻，且抽头位置较高，电压偏高需要吸收无功以减缓电压上升趋势。

图5 各时段变比抽头、电容器投入组数及光伏无功出力Fig. 5 Transformation ratio taps, number of capacitor input groups and photovoltaic reactive power output in each period

通过上述决策变量可求得系统电压分布，对比电压调控前后系统的电压偏差和电压波动如图5 所示，图6（a）中在电压调控前节点电压在时段10—12和16—20 内呈现较大的负偏差，在9、12—14 时段内呈现较大的正偏差，因此导致电压在10、12、16等时段内产生波动剧烈，接近10%左右如图5（c）中所示。如图6（b）所示，在电压调控之后电压偏差大部分处于正偏差，符合预期使电压尽可能的正偏差，且偏差率小于5%，同时电压整体波动小于2%如图6（d）所示，本文电压调控策略可有效减小电压偏差和平衡电压的剧烈波动。

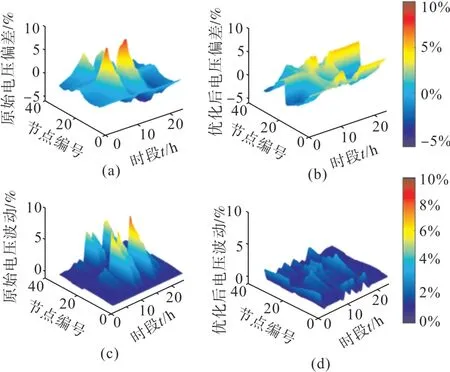
图6 优化前后电压偏差和波动对比曲面图Fig. 6 Comparison surface diagram of voltage deviation and fluctuation before and after optimization

4.2.2 采用不同重要程度系数的电压调控策略对比

进一步对比分析在场景2 下，不考虑负荷重要程度（方法1）、传统方法确定重要程度系数（方法2）以及本文方法确定重要程度系数（方法3）对电压条调控策略的影响。3 种方法计算求得的电压调控效益如图7 所示，不考虑负荷重要系数会因各负荷点缺乏区分度，导致调控效益值最低；而采用改进方法确定的负荷重要程度系数可有效提高电压调控的效益。如图8 所示优化后节点平均电压偏差小于+4%，平均电压波动降低到小于1%，本文电压调控策略有效减小电压偏差和波动。对比3 种方法可知，采用方法3 时重要程度较高的负荷节点（18、30 以及33）平均电压偏差和波动可获得更好的调节。方法可有效捕捉关键节点的信息并提供给电压调控策略进行优先治理，使得调控策略更具针对性。

图7 场景2下3种不同方法的优化结果对比Fig. 7 Comparison of optimization results of three different methods under scenario 2

图8 不同方法下节点电压平均偏差和波动对比图Fig. 8 Comparison diagram of average deviation and fluctuation of node voltage under different methods

4.2.3 新能源和负荷效益指标对电压调控的影响

为分析新能源效益和负荷用电效益指标对电压调控的影响，本文选取光伏场景2 下的光伏出力曲线，进一步选取弃光率、用户负荷等级以及用户满意度3个指标进行分析，划分以下4种需求情况。

1） 需求场景1：新能源的弃光率相同且所有用户负荷等级和满意度均一致，满足电能质量标准即可；

2） 需求场景2：拟定在场景1 下节点18、33 的弃光率较大，要求电压调控侧重降低系统的弃光率；

3） 需求场景3：场景1 下使得节点16—18、31—33用户满意度较低，要求提高用户群的满意度；

4） 需求场景4：场景1 下设节点8—10、30—31负荷为一级重要负荷，电压偏差小于±2%。

不同需求场景下求的各指标权重如表4 所示，各负荷节点的重要程度系数如图9 所示。相对于场景1，场景2 中弃光率（P11）、场景3 中用户满意度（P32）以及场景4 中负荷等级（P31）权重显著增大。由于不同场景下对应指标差距变大，权重增大可有效体现各个负荷节点之间的需求差异。场景2 中节点18、33 重要程度系数高于场景1，这是由于节点18和33处电压越上限导致弃光率较高，同时P11权重较高，故负荷重要程度系数较大，认为其节点电压调控更为迫切，所带来的新能源效益较高；场景3 中用户满意度权重高，满意度较低的重要程度系数高，满意度较高的重要程度系数低，电压调控将针对性的注重满意度较低节点电压进行调节，弱化满意度较高节点的调节；场景4 中负荷等级权重高，社会效益占主导，一级负荷的重要程度系数高于其余节点，调控节点电压可提高系统整体社会效益。

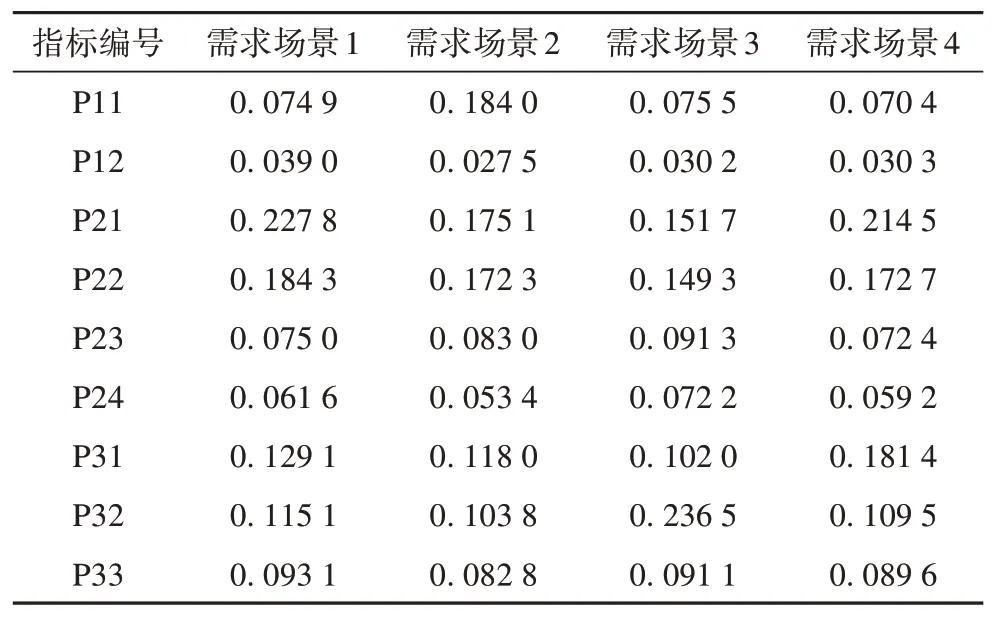
表4 不同需求场景下负荷重要指标综合权重Tab. 4 Comprehensive weight of important load indicators under different demand scenarios

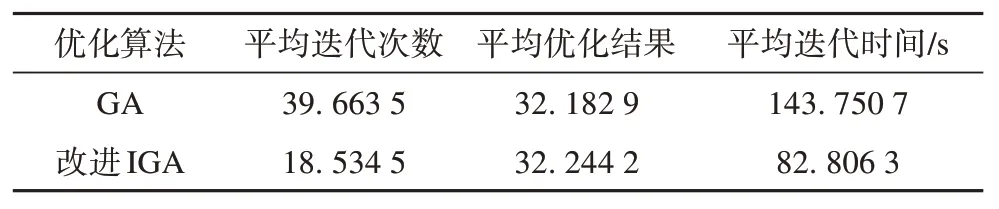
表5 算法全天计算结果对比Tab. 5 Comparison of whole day calculation results of the algorithm

图9 不同需求场景下各节点的重要程度系数Fig. 9 Importance coefficient of each node under different demand scenarios

场景1、2 调节结果如图10 所示，在满足相同的电能质量需求下，如图10（a）中场景2 在12—14时段，通过降低主变档位，降低系统整体电压、降低弃光点功率因数，使得18、33 节点光伏并网功率增加，14 时段弃光率由16.69%降低至7.08%，调控效益由33.013 增大至34.715。如图10（b）所示，C3投入组数减小可降低弃光点电压，C1—2负责提高非光伏接入点电压。因为此时弃光点的重要程度系数大，场景2 的调控方式所带来的效益更高。

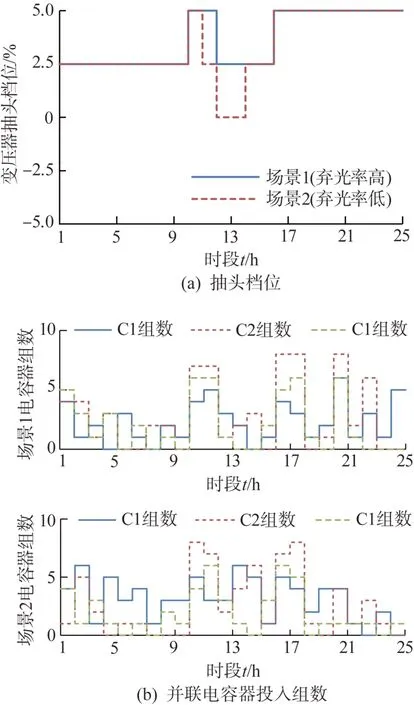
图10 场景1和2电压调控策略图Fig. 10 Scenario 1 and 2 voltage regulation strategy diagram

场景1 和3 下采取不同的电压调控策略后节点电压分布如图11所示，场景1中两个用电满意度较低的用户群（节点16—18、31—33）电压偏差范围分别为［-0.03，0.05］，［-0.03，0.03］，而场景3 下分别为［-0.01，0.02］，［-0.02，0.01］，电压偏差和波动显著减小，调控效益增大。这是由于场景3用户的用电质量不满意度增加，表4 中P23 权重增大，节点重要程度系数增大，调控策略集中无功资源优化满意度较低区域的电压以提高用户满意度，取得最大调控效益。

图11 场景1和3用户满意度较低节点电压分布图Fig. 11 Voltage distribution of nodes with low user satisfaction in scenario 1 and 3

同理分析场景1 与场景4，两个重要负荷区域（节点8—10、30—31）电压偏差范围均为［-0.03，0.03］，而场景4 下均为［-0.02，0.02］，电压偏差和波动显著较小，重要负荷电压质量得到保证，在可满足重要负荷更高的电压需求，从而增大调控效益。

电压调控策略可以在电压满足基本要求下，面对不同用户和新能源需求时仍能进行针对性的电压治理。可有效调动有限的无功调压资源针对性的处理光伏接入导致的电压问题，提高系统光伏接入量，降低弃光率，提供新能源效益。同时针对性解决重要负荷高用电质量要求且用户负荷的用电满意度较低等问题，达到降低投诉率效果，提高社会效益。

4.3 算法对比分析

本文分别采用传统遗传算法和改进遗传算法对场景2 下进行电压调控，如图12 所示，在时段11传统GA 出现了局部收敛现象，计算效率低；如表4 所示，相比GA 本文改进的IGA 平均迭代次数少，收敛速度较快，平均计算时长段。

图12 场景2迭代对比图Fig. 12 Scenario 2 iteration comparison diagram

5 结论

针对传统电压调控策略难以应对高渗透率光伏接入中压母线后电压的双向越限且波动剧烈，欠考虑负荷重要程度影响电压调控策略的问题。本文主要开展了以下工作。

1） 从源网荷三方面建立负荷重要程度指标体系，基于改进AHP 和改进CRITIC 的组合变权法可有效增大节点评估值的区分度，并突出不同场景下指标的薄弱环节，劣化度较高的指标权重较大，电压调控需求较高节点赋予较高的效益系数，权衡源网荷侧的调控效益。

2） 建立了考虑负荷重要程度的含DG 配电网的电压调控优化模型，在不同光伏出力下策略均可改善电压双向偏差和减小电压波动。同时可有效捕捉关键节点的信息并提供给电压调控策略进行优先治理，使得调控策略更具针对性。

3） 本文对传统GA 算法进行改进，相较于传统算法其迭代次数少、可有效避免局部收敛，计算结果准确，计算效率高。