三角代数上的可乘映射

刘 磊, 李开鹏, 王绪迪

(1.西安电子科技大学 数学与统计学院, 陕西 西安 710071; 2.西安理工大学 理学院, 陕西 西安 710054)

多年来,如何刻画代数上在某点可导的映射受到许多数学家的关注。对于某些代数,几位作者讨论了G分别为零、单位元、非平凡幂等元、可逆元素的情况[1-6]。

受可导映射启发,如果对S,T∈A使得ST=G时就有φ(ST)=φ(S)φ(T),则称可加映射φ在G处可乘。对于可乘映射的研究也有相关结果。Zhu等[7]研究了矩阵代数上在可逆元和单位元处可乘的映射。Gong等[8]研究了矩阵代数上某些点Jordan可乘的映射。Li等[9]刻画了在含有单位元的Banach代数上分离点和单位元点处可乘的映射。Burgos等[10]在研究了C*-代数上在零点、单位元点和投影点上可乘的映射。

如何刻画三角代数上在任一固定点可乘的映射是一个很自然的问题。但是,到目前为止,还未见到此方向上的研究成果。本文描述了在三角代数上任一固定点可乘映射的结构,将结果应用到了套代数上。

1 预备知识

2 主要结论与证明

(i) 对任意的a∈A,存在某个正整数n满足nIA-a在A中是可逆的;

(ii) 对任意的b∈B,存在某个正整数n满足nIB-b在B中是可逆的。

则对任意的A,B∈T,φ(AB)=φ(A)φ(B)成立,即φ是T到U上的同态映射。

断言1对任意的a∈A,有f12(a)=0,f22(a)=0。

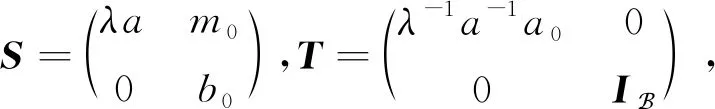
(1)

其中:

由式(1)可得,对于任意可逆的a∈A,有:

由此可知,对于任意可逆的a∈A,有f12(a)=0,f22(a)=0。

由假设 (i)得,对于任意a∈A,存在正整数n,使得nIA-a在A中可逆。因此,对任意的a∈A,有f12(nIA-a)=0,f22(nIA-a)=0。又由于nIA在A中可逆,故对于任意a∈A,f12(a)=0,f22(a)=0。

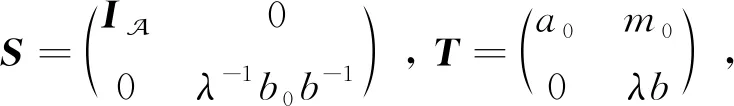
断言2对任意的b∈B,h11(b)=0,h12(b)=0。

断言3对任意的m∈M,g11(m)=0,g22(m)=0。

(2)

其中Δ=(g22(m0-λm)+h22(b0))(ID+g22(m))。

由式(2)可知,对任意的m∈M,有:

(3)

g22(m0)+h22(b0)=

(g22(m0-λm)+h22(b0))(ID+g22(m))

(4)

由式(3)、(4)可得:

g11(m)+g11(m)g11(m)=0

(5)

g22(m)+g22(m)g22(m)=0

(6)

将等式(5)和等式(6)中的m用-m替换,有:

-g11(m)+g11(m)g11(m)=0

(7)

-g22(m)+g22(m)g22(m)=0

(8)

对任意的m∈M,比较等式(5)和等式(7),有g11(m)=0。类似地,比较等式(6)和等式(8),有g22(m)=0

(9)

断言4对任意的a∈A和m∈M,g12(am)=f11(a)g12(m)成立。

(10)

由式(10)可得:

g12(m0)=λf11(a)g12(m)+g12(m0)-λg12(am)

因此有g12(am)=f11(a)g12(m)。 由假设 (i)可知,对任意的a∈A,存在一个整数n使得nIA-a在A中是可逆的。所以对任意的a∈A和m∈M,有g12((nIA-a)m)=f11(nIA-a)g12(m)。注意到nIA是可逆的,最终推断出对任意的a∈A和m∈M,有g12(am)=f11(a)g12(m)。

断言5对任意的b∈B和m∈M,有:g12(mb)=g12(m)h22(b)。

断言6对任意的a1,a2∈A,f11(a1a2)=f11(a1)f11(a2)。

对任意的a1,a2∈A和m∈M,应用断言 4,一方面,有:

g12(a1a2m)=f11(a1a2)g12(m)

另一方面,再一次使用断言 4,有:

g12(a1a2m)=f11(a1)g12(a2m)=

f11(a1)f11(a2)g12(m)

比较这两个等式可知:

(f11(a1a2)-f11(a1)f11(a2))g12(m)=0

由于φ是满射并且N是忠实的,所以从上式可得对任意的a1,a2∈A,f11(a1a2)=f11(a1)f11(a2)。

对任意的b1,b2∈B和m∈M,应用断言 5,一方面,有:

g12(mb1b2)=g12(m)h22(b1b2)

另一方面,再一次应用断言 5,有:

g12(mb1b2)=g12(mb1)h22(b2)=g12(m)h22(b1)h22(b2)

通过和断言6类似地讨论,易得如下断言。

断言7对任意的b1,b2∈B,等式

h22(b1b2)=h22(b1)h22(b2)成立。

断言8定理1成立。

由等式(9)及断言 4～7可知,对任意的

直接计算可得:

即φ是T到U上的同态映射。

3 应 用

令H是实或复的Hilbert空间。众所周知,H上的套是H上的正交投影链,在强算子拓扑中是封闭的,并且包含0和单位算子I。如果一个套包含至少一个非平凡投影,则称其为非平凡的套。由algN表示与N关联的套代数,它是由所有保持N不变的有界线性算子组成的算子代数。很明显,每个非平凡的套代数都是三角代数。所以有以下推论。

证明由条件易知与N关联的套代数可以用H=ran(P)⊕ran(P)⊥和H=ran(Q)⊕ran(Q)⊥表示为两种三角代数,并且满足定理1中的条件。因此由定理1可得φ是algN上的自同构。又因为套代数上的每个自同构都是空间的(参见文献[12]),所以存在可逆算子S∈algN满足对任意的A∈algN,有φ(A)=SAS-1。

4 结 论

本文刻画了三角代数上在固定点可乘的可加映射,证明了在任一固定点可乘的可加满射一定是同态映射。作为应用,证明了套代数上在固定点可乘的可加双射在一定条件下一定是自同构。