交错布局轻型四坡房屋群风致干扰效应研究

颜卫亨, 王西凤, 代 鹏

(长安大学 建筑工程学院, 陕西 西安 710061)

轻型四坡房屋布置方便快速、机动性强,广泛应用于野营房屋、灾后安置和大型工程建设项目临时用房中,同时也属于风敏感低矮房屋,风荷载往往是其控制荷载。而此类房屋使用时常以群体布置出现,交错布局也是群体布置的常见形式。群体布置当房屋间距小于临界间距时,房屋之间存在风致干扰效应。而我国《建筑结构荷载规范》[1]仅规定了平面矩形高层建筑相互干扰的群体效应,对低矮建筑的群体风致干扰效尚未明确规定。国外荷载规范对低矮建筑群风致干扰效应也未见取值方法[2-3]。国内外关于群体干扰效应的研究大多针对大型冷却塔、高层建筑和其他形体低矮房屋[4-9],对于轻型四坡房屋在交错布局下的群体干扰效应尚未有相关研究。实际应用中若仅参考单体房屋体型系数进行交错布局抗风设计,则存在安全隐患。

本文通过与TTU实测结果对比验证数值模拟可行性,确定数值风洞主要技术参数,利用数值模拟方法进行交错布局四坡房屋群风致干扰效应研究,以期有效应对干扰效应的不利影响,为轻型四坡房屋群体规划布局和结构设计提供参考依据。

1 数值模拟基础性研究

1.1 边界条件的设定

数值模拟时计算域入口设置为速度入口,出口采用完全出流,侧壁和顶面设置为对称边界,流场地面和模型表面设置为无滑移壁面[6, 10-11]。选取非平衡壁面函数能更好地模拟气流在钝体周围的碰撞、分离、再附、回流和旋涡等复杂流动现象。

大气边界层平均风剖面按文献[1]采用指数率描述如下式:

(1)

数值模拟时与TTU实测对应,A类地貌取α=0.12,U0取离地10 m高度处平均风速10 m/s。

流域入口湍动能k和湍流耗散率ε取值如下:

k=1.5(UIu)2

(2)

ε=0.090.75k1.5/l

(3)

式中:l=0.07L代表湍流积分尺度,其中L为建筑物特征尺寸;湍流强度Iu参照文献[3]给出的取值范围。

利用UDF编程将以上公式与Fluent作接口导入。

1.2 计算域大小

数值模拟精度与计算域大小密切相关,计算域太大会增加网格数量,影响计算效率,太小则无法准确模拟建筑物风压分布特性。对于低矮建筑,若其高度为H(群体布置为最高建筑物高度Hmax),计算域入口距建筑迎风面应大于4～5H,顶壁和侧壁与建筑顶面和侧面的距离应大于4H。建筑模型背风面后的气流流动应能够充分发展,通常情况下模型背风面与出口的距离应大于9～10H。同时,数值模拟时模型的阻塞比不宜大于5%[6,11-12]。

基于计算流体动力学软件Fluent,控制阻塞比小于3%,建立三种不同尺寸的计算域对图1中90°风向角下TTU低矮建筑模型横向中轴线1～11监测点进行数值模拟,结果见图2。图2中,为提高计算效率,在首先保证计算精度的基础上,计算域尺寸选用150 m×100 m×60 m精度较高。

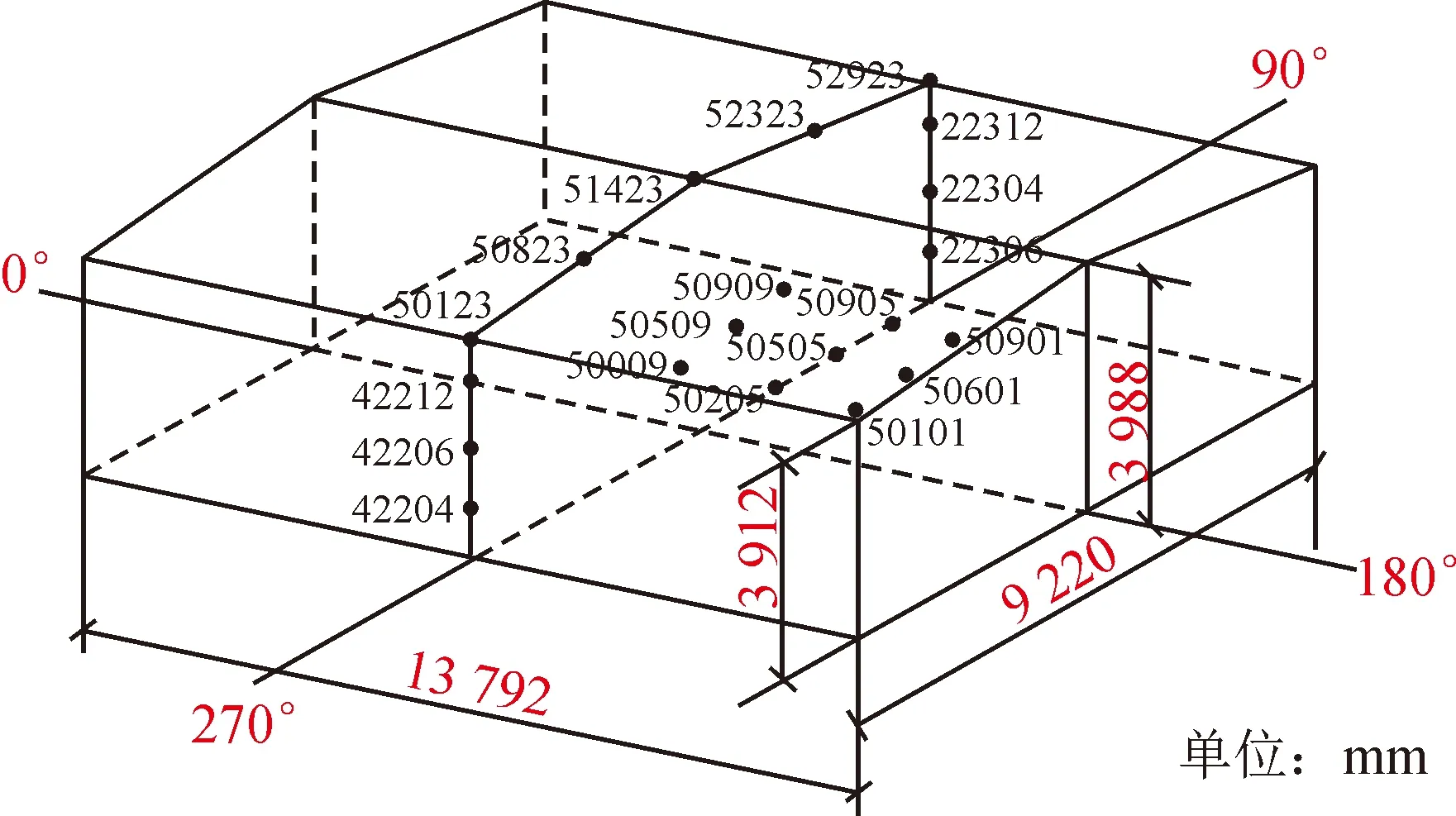
图1 TTU低矮建筑尺寸及典型测点分布

图2 不同计算域大小下TTU模型1～11测点平均风压系数

1.3 网格划分方式及数量

网格是CFD数值模拟和分析的载体,也是分析模型的几何表达方式。网格分为结构化网格和非结构化网格,结构化网格节点排列有序、相邻点之间的关系明确,网格适应了几何体的规则形状。非结构化网格无法用固定法则对节点位置加以命名,网格生成复杂,但其对复杂边界有极强适应性和有效性。本文为提高计算效率,采取在模型所在的核心区采用灵活的非结构化网格,在外围区域采用计算效率高的结构化网格的分区混合网格划分形式[11-12]。

选择计算域大小为150 m×100 m×60 m,对三种网格数量下TTU模型进行数值模拟计算,所得结果见图3。由图3,网格数量越大,数值模拟与实测结果越接近,但网格过密则计算耗时过长,考虑计算精度同时兼顾计算效率,取网格数量为224.6万,数值模拟时控制网格数量在2.5个/m3左右。

图3 不同网格数量下TTU模型1～11测点平均风压系数

1.4 湍流模型和离散格式

控制单参数变化,对不同湍流模型和离散格式下TTU模型进行数值模拟,结果见图4。

图4 不同湍流模型及离散格式下TTU模型1～11测点平均风压系数

由图4(a),除标准k-ε模型在背风向误差偏大外,其他4种湍流模型均能较好的预测各监测点的风压系数,对比知RNGk-ε模型精度较高,本文湍流模型采用RNGk-ε模型。由图4(b),三种对流项离散格式中,一阶迎风格式数值耗散较大,作定量分析误差较大,而二阶迎风格式计算精度较高,故本文采用二阶迎风格式。

综上,采用数值模拟方法对TTU低矮建筑进行分析与实测数据吻合较好,说明利用数值模拟对低矮房屋表面风压分布规律进行研究是可行有效的。

2 轻型四坡房屋群数值模拟

2.1 研究对象

本文研究对象为应用较广泛的轻型四坡房屋,房屋外形和三维尺寸见图5(a)。群体布置时房屋表面较单体会出现放大和遮挡效应,气流在房屋表面的碰撞、分离、再附、回流和旋涡等流动现象比单体表面复杂。结合四坡房屋表面物理分区和双轴对称特点,选取0°,45°,90°三种风向角并对房屋表面分区见图5(b)所示。

2.2 群体交错布局及参数选取

由文献[13],群体布置时房屋之间应有大于2 m的人行通道。经对图6(a)中0°风向角下三个四坡房屋交错布置的试算,由图6(b)知,房屋间距达到24 m时,房屋表面各区平均风荷载系数与单体基本相同,因此可认为24 m为群体干扰效应消失的无干扰间距,房屋间距布置在2～24 m之间。

结合轻型四坡房屋使用情况,设计了如图7所示8个四坡房屋交错布局的布置方式。为反映群体布置的疏密程度,探讨群体风致干扰效应随疏密程度的变化规律,根据交错布局时四坡房屋间距与房屋平面对应尺寸的相对关系,定义无量纲的疏密系数为:

图7 四坡房屋交错布局

Rx=Sx/L= 0.5, 1, 1.5, 3, 5

(4)

Ry=Sy/B= 0.5, 1, 1.5, 3, 5

(5)

式中:Rx、Ry表示横、纵向疏密系数;Sx、Sy为交错布局的横、纵向间距,取Sx= 0.5L,L, 1.5L, 3L, 5L,Sy= 0.5B,B, 1.5B, 3B, 5B,其中L和B分别为房屋长度和宽度。图7中黑体房屋为所研究的目标房屋,各风向角下处于迎风前排的房屋为目标房屋一,处于后排的为目标房屋二。

2.3 风压系数等值线

以3个风向角和5种横、纵向疏密系数为参数,进行75种工况数值模拟,得到目标房屋表面风压系数等值线。限于篇幅,本节取90°风向角时最具代表性的Rx=0.5,Ry=0.5和Rx=3,Ry=5时的目标房屋表面风压系数等值线云图进行分析,目标房屋各区域风压系数等值线见图8～11。

由图8,90°风向角下,单体房屋迎风山墙C区受正压控制,风压系数呈环状分布,迎风山墙中上部出现正压极值0.9,由中心向外侧递减,直至迎风山墙边缘处出现负压,负压极值为-0.2。目标房屋一C区风压分布基本不受疏密系数变化的影响。当Rx=Ry=0.5时,由于上游及同排房屋的遮挡和干扰,与单体房屋相比,目标房屋二迎风山墙风压系数出现变号现象,表现为整个C区受负压控制,负压极值为-0.36。当Rx=3,Ry=5时,由于房屋群布置间距较大,目标房屋二迎风山墙风压分布规律与单体房屋相似,但风压系数值较单体房屋为小。

由图9,单体房屋背风山墙D区受负压控制,负压极值-0.25。交错布局下,当Rx=Ry=0.5时,目标房屋一背风面主要承受负压,D1和D2区负压值外侧较内侧为大。但由于房屋布置较密,流经背风面的气流受到后排房屋的碰撞后形成回流,在目标房屋一背风面中下部出现小块低正压区域,从而使其背风面平均风荷载系数绝对值较单体减小。Rx=3,Ry=5时目标房屋一D区风压分布与单体近似。不同疏密系数下目标房屋二D区风压分布与单体近似。

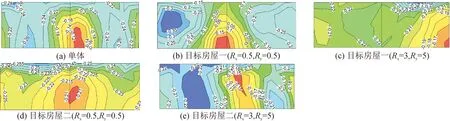
图9 90°风向角典型疏密系数下目标房屋背风山墙风压系数等值线

由图10,单体房屋屋面受负压控制,负压极值-1。流经屋面的气流在迎风屋面C区屋脊线附近出现较强的气流分离,屋脊线处出现高负压区域,然后经屋脊线向后发展并再次附着到侧风屋面和背风屋面上,形成再附。Rx=Ry=0.5时,目标房屋一同排及后排其他房屋的存在抬升了经由其迎风屋面屋脊线处出现分离而向后发展的气流,减弱了气流在侧风和背风屋面的再附程度,目标房屋一侧风屋面A、B区及背风屋面D区风压系数绝对值较单体有所减小,出现遮挡效应,D3和D4区遮挡效应最为明显;但对于目标房屋二,来流经上游房屋抬升使其迎风屋面C3和C4区风压系数绝对值较单体有所增大,出现了放大效应。Rx=3,Ry=5时,由于房屋群间距较大,两目标房屋屋面风压分布与单体近似。

图10 90°风向角典型疏密系数下目标房屋屋面风压系数等值线

由图11,单体房屋侧面B区受负压控制,侧面上游B1区边缘处风压系数变化梯度大,B1区风压系数绝对值也较大,负压极值-0.85,侧面下游B2区负压值较小,梯度变化均匀。Rx=Ry=0.5时,在交错布局下,房屋布置较密,目标房屋一与两侧其他房屋间形成狭窄气流通道,此时顺风向纵向间距较小,气流流经此通道时形成急流出现峡谷效应,导致目标房屋一B1、B2区风压系数较单体有所增大,出现了放大效应;同时,由于上游房屋的干扰和遮挡,目标房屋二B区出现了遮挡效应,B1区上游脚部出现小块低正压区域。Rx=3,Ry=5时,目标房屋B区风压分布与单体相似。

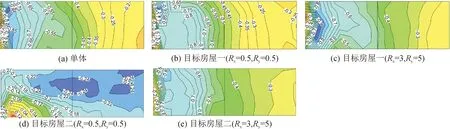
图11 90°风向角典型疏密系数下目标房屋侧面风压系数等值线

3 风致干扰效应

为分析群体交错布局时的风致干扰效应,引入干扰因子IFμ量化交错布局下目标房屋相对于单体房屋的受扰程度。干扰因子IFμ定义为:

(6)

式中:μSI为单体房屋的平均风荷载系数;μSA为受扰后房屋的平均风荷载系数。

IFμ绝对值大于1,说明出现放大效应;IFμ绝对值小于1,说明出现遮挡效应;IFμ小于0,说明受扰前后风压反向;IFμ绝对值在[0.95, 1.05]时,认为无干扰[6,14]。本节以45°和90°风向角时为例对风致干扰效应展开分析。

3.1 45°风向角干扰效应

45°风向角下目标房屋干扰因子变化趋势分别见图12和图13。

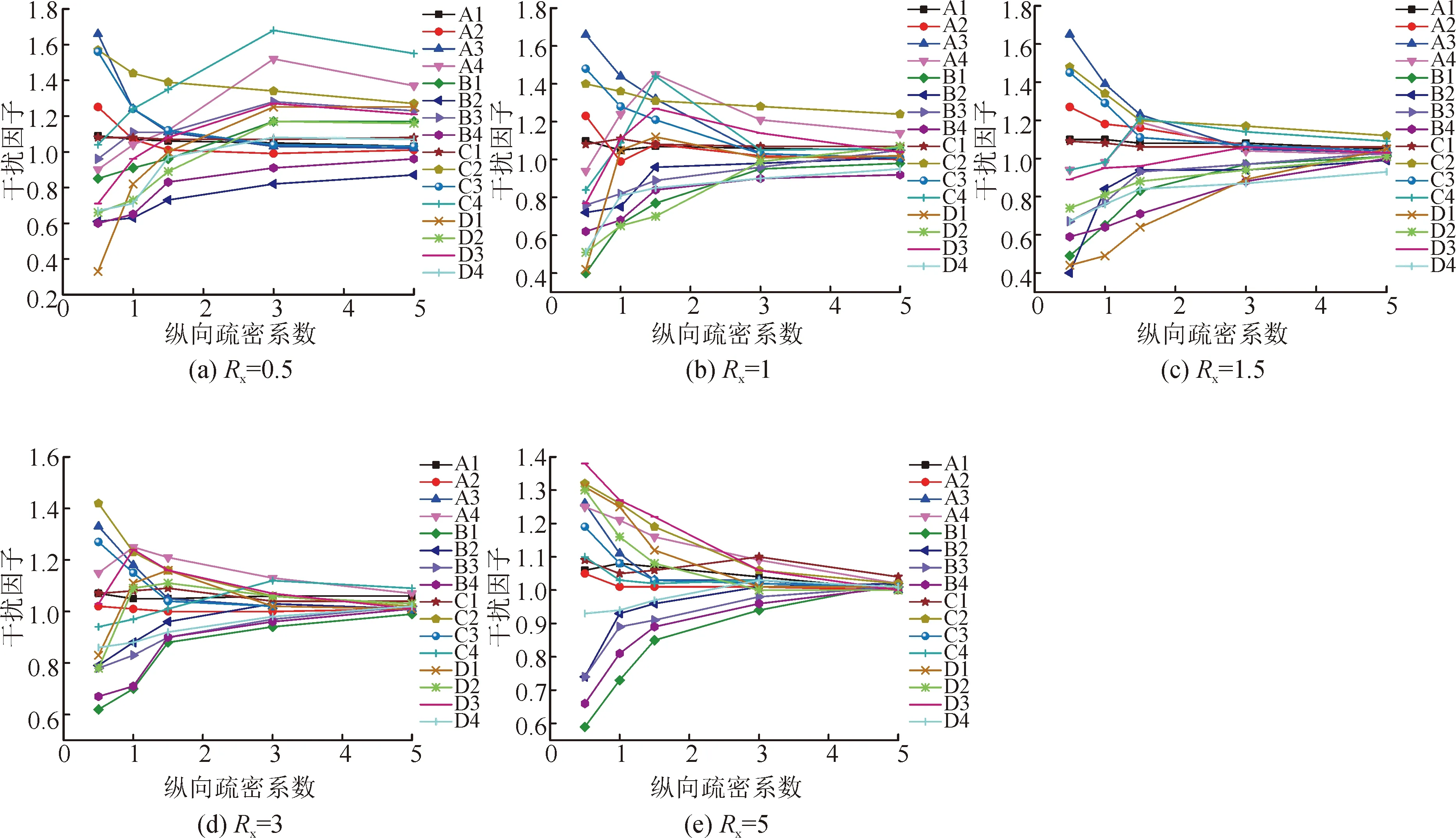
图12 45°风向角目标房屋一干扰因子

图13 45°风向角目标房屋二干扰因子

见图12,交错布局下目标房屋一表面各区域既有放大效应也有遮挡效应。当疏密系数较小,Rx=0.5和0.5≤Ry≤1.5时干扰效应最为显著。此时,目标房屋表面大部分区域均出现较强的放大效应,如迎风屋面A4、C3区,迎风山墙C2区,背风山墙D2区及背风屋面D3区干扰因子最大值均大于等于1.38。该风向角下最大干扰因子1.68出现在Rx=1.5且Ry=3时的C4区,平均风荷载系数较单体增大了68%,群体风致干扰效应不可忽略。随着纵、横向疏密系数的增加,目标房屋表面所有区域干扰效应趋于稳定,干扰因子值逐渐接近于1。当Rx≥3且Ry≥5时,干扰效应基本消失。

见图13,目标房屋二表面出现明显放大效应和风压反号现象,干扰效应强于目标房屋一。当疏密系数较小,Rx=0.5和0.5≤Ry≤1.5时干扰效应最为突出,迎风屋面A4、C3、C4区,迎风山墙C2区,背风山墙D1、D2区和背风屋面D3区的干扰因子最大值均大于等于1.70。该风向角下目标房屋所有区域的干扰因子最大值3.41出现在Rx=3且Ry=0.5时目标房屋二A3区,平均风荷载系数较单体增大了241%,干扰效应较强,设计时应予以重视。迎风屋面上游A3、C3区为受干扰程度最重的区域,房屋布置较密,0.5≤Rx≤1.5且0.5≤Ry≤1.5时,这两个区域出现明显的风压变号现象,最大负干扰因子-3.03出现在Rx=0.5且Ry=0.5时C3区,相比于单体房屋,风压变号且平均风荷载系数绝对值增大了203%。随着疏密系数的增加,目标房屋表面各区干扰效应趋于稳定,干扰因子值逐渐接近于1。当Rx≥3且Ry≥5时,干扰效应基本消失。

综上,45°风向角下群体风致干扰效应不可忽略。疏密系数为影响群体风致干扰效应强弱的关键参数,0.5≤Rx≤3,0.5≤Ry≤1.5时,干扰效应较强;随着疏密系数增大,当Rx≥3且Ry≥5时干扰效应消失。

3.2 90°风向角干扰效应

90°风向角下目标房屋干扰因子变化趋势分别见图14和15。

见图14,目标房屋一大部分区域表现为放大效应,局部出现弱遮挡效应。除Rx=0.5时D1和D2区外,其他区域干扰因子随疏密系数的增大而接近于1。0.5≤Rx≤1.5,0.5≤Ry≤3时,目标房屋一各区干扰因子随Ry变化而变化幅度较大,此时保持Ry不变,干扰因子随Rx增大而逐渐减小。目标房屋一最大干扰因子1.64出现在Rx=0.5且Ry=3时迎风屋面C区。对于Rx=0.5时背风面D1和D2区,随着Ry由0.5增至5,干扰因子由0.79增至1.56,0.5≤Ry≤1.5时出现遮挡效应,3≤Ry≤5时出现放大效应。这是因为Rx较小,顺风向的Ry也较小时,气流经目标房屋一与两侧房屋间形成的狭窄气流通道向后发展时与后排房屋碰撞形成回流,导致背风面负压绝对值值较单体为小。而Ry较大时,气流能充分向后发展,在背风面出现较高负压,Ry=5时放大效应最强,较单体放大了1.56倍。Rx≥5且Ry≥3时,各区域干扰因子接近于1,干扰效应基本消失。

见图15,目标房屋二主要表现为遮挡效应,但局部区域的放大效应不容忽视。Rx=0.5且Ry=1时A1和B1区遮挡效应最强,平均风荷载系数较单体分别减小了75%和82%。当0.5≤Rx≤1.5,0.5≤Ry≤1.5时,C区干扰因子为负,表明该区在交错布局房屋间距较密时相比单体会出现风压反向现象。然而90°风向角下最大干扰因子1.67出现在Rx=1且Ry=0.5时背风面D区,平均风荷载系数较单体房屋增加了67%,这表明,对于处于下游受遮挡位置的目标房屋二,虽然其表面大部分区域出现遮挡效应,但房屋部分区域仍会出现较强放大效应,放大效应不可忽略。随着疏密系数的增大,干扰效应逐渐减弱,当Rx≥5,Ry≥3时,干扰效应基本消失。

综上,90°风向角下,群体风致干扰效应不可忽略。疏密系数为影响群体风致干扰效应强弱的关键参数,当0.5≤Rx≤5,0.5≤Ry≤3时,干扰效应较强;随着疏密系数增大,当Rx≥5且Ry≥3时干扰效应消失。

4 风荷载体型系数

表1为单体房屋各区平均风荷载系数和目标房屋各区最大干扰因子。当房屋间距小于临界间距时,干扰效应不可忽略。实际应用时若仅参考单体体型系数进行群体抗风设计,则存在安全隐患。为计及交错布局带来的放大效应,根据四坡房屋使用情况,房屋表面没有分区且不会有特定迎风面、侧面、迎风屋面或背风面,在表1基础上,结合四坡房屋双轴对称的特点,按照最不利系数包络原则,将房屋表面简化为迎风山墙、其他山墙和屋面三个区域,在单体房屋表面各区域体型系数上乘以最大干扰因子作为放大因子,得到交错布局时的风荷载体型系数见图16。

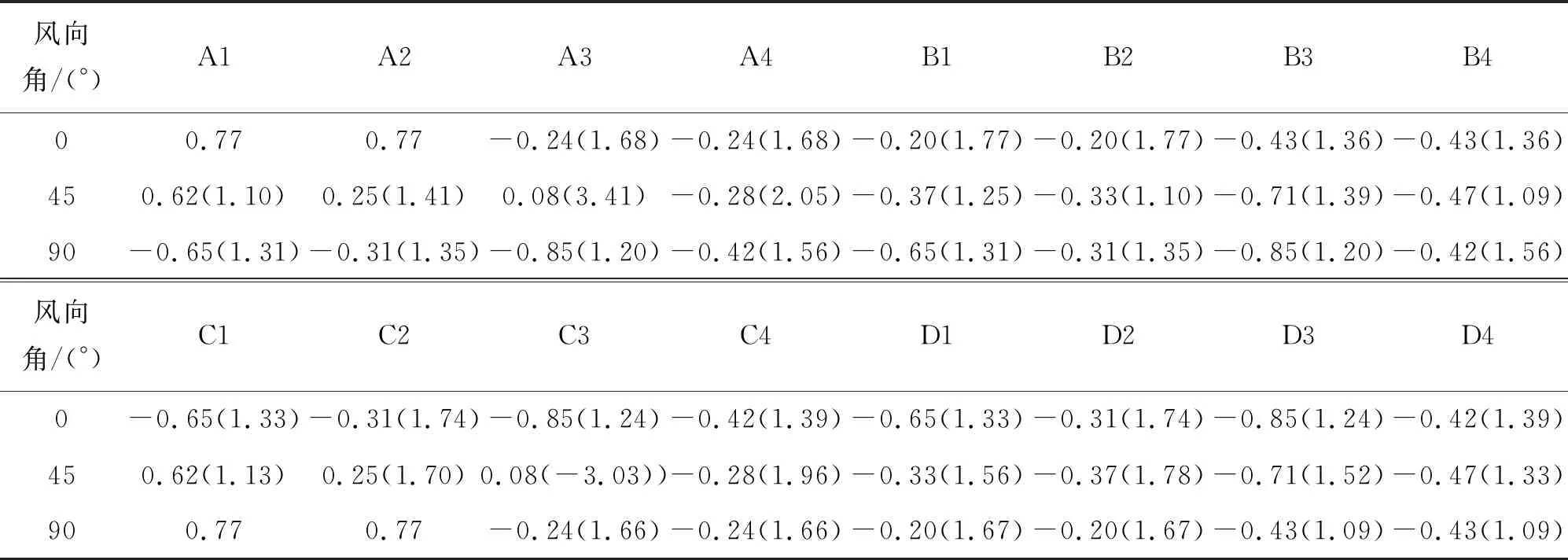
表1 单体房屋各区平均风荷载系数和目标房屋最大干扰因子

图16 交错布局下轻型四坡房屋风荷载体型系数

图16中正号表示风压力,负号表示风吸力,括号中数值为放大因子,交错布局轻型四坡房屋风荷载体型系数为单体房屋体型系数与放大因子的乘积,Rx≥5且Ry≥5时群体干扰效应基本消失,此时可按单体房屋体型系数进行抗风设计。

5 结 论

1) 对于交错布局轻型四坡房屋群风致干扰效应的数值模拟控制网格数量2.5个/m3,湍流模型采用RNGk-ε模型,离散格式采用二阶迎风格式是可行有效的。

2) 风向角一定时,疏密系数为影响群体风致干扰效应强弱的关键参数。交错布局房屋布置间距分别为:0°风向角下1倍房屋长度和1倍房屋宽度、45°风向角下3倍长度和1倍宽度、90°风向角下1倍长度和0.5倍宽度时干扰效应最强。

3) 0°风向角交错布局房屋布置间距大于等于3倍长度和5倍宽度;45°风向角大于等于3倍长度和5倍宽度;90°风向角大于等于5倍长度和3倍宽度;所有风向角下大于等于5倍长度和5倍宽度时干扰效应消失。

4) 0°,45°,90°风向角下,群体交错布局时目标房屋与单体房屋相比,出现最强放大效应区域的平均风荷载系数分别放大了1.77倍,3.41倍,1.67倍;45°风向角时干扰效应最强。房屋群间距小于临界间距时,群体干扰效应不可忽略,实际设计中应引起重视。

5) 在单体房屋体型系数基础上乘以放大因子以计及交错布局相对于单独布置的干扰效应,得到交错布局轻型四坡房屋风荷载体型系数(见图16)。