强震作用下反倾薄层岩质斜坡倾倒破坏机制及动力响应研究

龚逸非, 姚爱军, 谷坤生, 李彦霖, 田 甜

(北京工业大学 城建学部,北京 100124)

三江流域横跨深切的青藏高原东南部和青藏高原北部,该区域内地形、气候多变,新构造运动强烈,地震活动频繁,导致地质灾害频发[1-2]。2008年的汶川地震诱发了两千多处滑坡,根据地震诱发的大量滑坡调查统计[3],在地震作用下顺层岩质滑坡所占的比例最大,但是反倾岩质斜坡岩层往往包含多种岩性,呈现软硬互层、厚薄互层等现象,岩层内部还往往发育着节理、裂隙,构成层状复合岩体边坡[4],对于其的研究更具有难度。目前对于岩质斜坡的动力响应规律以及变形破坏模式的方法主要有现场调查、数值模拟和物理模型试验三种方法。

其中数值模拟以其适应广、数据全、成本低等优势被广泛应用,其中三维离散元程序在模拟完整岩石的破裂过程、岩石断裂现象及裂隙发育过程等具有巨大优势[5],常常作为现场勘查的反演和试验结果验证的方法来使用。杨忠平等[6]采用振动台试验与数值模拟结合,对比了顺层和反倾两类岩质边坡在反复微小地震作用下的稳定性。谢良甫[7]引入了新的斜坡稳定性评价指标,利用数值模拟的方法,分别基于最大位移、总位移以及变形区范围3个指标进行讨论,并结合3个指标进行斜坡稳定性的敏感性分析,并引入能量场的概念,详细分析了倾倒变形的变形演化阶段。岑夺丰等[8]用颗粒流PFC(平行黏结模型)模拟方法对反倾厚层边坡的破坏演化机制进行了研究。言志信等[9-10]运用Flac3D分别建立受地震作用的含软弱层岩质边坡以及顺倾岩质边坡锚固数值模型,着重研究了水平和竖向相互耦合的地震波下的锚杆锚固界面上的剪切作用。

振动台模型试验能直观的研究地震荷载下各类斜坡的破坏问题,具有可重复性等优点,被广大研究者所采用。我国对振动台的研究从1960年开始,前期发展较为缓慢[11],自2008年汶川地震后引起国家和学者对地震引发的滑坡灾害的重视,促进了振动台试验对于滑坡模拟的飞速发展。巨能攀等[12]采用地质详勘和案例类比的方法,构建并完善了顺层和反倾岩质斜坡变形破坏的概念模型,并采用大型振动台试验对比两者在强震条件下的动力响应和失稳模式。刘汉东等[13]进一步深入研究了反倾层状岩质斜坡对低频输入波的高程放大效应和对高频的趋表效应。杨国香等[14-15]采用振动台试验分析了地震动参数对反倾层状岩质边坡动力放大系数影响,得出在接近斜坡自振频率时加速度放大系数最大,讨论了幅值变化对于动力响应以及坡体分布规律的影响。Gischig等[16]对地震波在岩质斜坡中的放大效应与同震位移之间的相关性进行敏感性分析,着重讨论坡度、岩性差异和岩体结构对放大效应的影响。

经大量研究表明斜坡在受地震作用下的破坏模式和破坏程度受岩层在发育的结构面的影响(包括断层、软弱夹层等)很大[17]。张家明[18]提出软弱夹层使得研究岩质斜坡的变形-破坏机理更为复杂,严重影响其稳定性。周逸飞等[19]对含软弱夹层的斜坡在地震作用下的动力特征做了初步研究。上述研究表明,输入地震动参数和岩层中发育的各种结构面影响斜坡的动力响应和破坏机制。

目前对于含软弱破碎带的薄层反倾岩质斜坡在地震作用下的响应及变形破坏的研究并不充分,同时对于岩质边坡的地震波输入方案,多选用土壤波和正弦波,考虑基岩地震波输入的研究较少。本文以金沙江左岸宗绒反倾岩质斜坡为研究原型,通过振动台缩尺试验研究了薄层反倾岩质边坡的动力响应和变形-破坏阶段,采用改变地震动参数以及地震波类型,研究反倾岩质斜坡从位移变化、宏观变形到的起裂和失稳的临界条件,着重讨论了软弱破碎带对斜坡动力响应的影响。

1 振动台试验概况

1.1 模型概化

本试验以金沙江左岸历史性堵江滑坡宗绒滑坡为原型设计振动台试验。根据现场调研,宗绒滑坡所在边坡地层出露的主要岩性从下至上依次为云母片麻岩、古生界蛇绿岩(斜长角闪岩)构成的反倾层状岩质边坡。现场调查表明,该滑坡为反倾岩层的倾倒破坏导致的,预计体积5×107m3,坡底分布大量滑坡堆积物、残余滑坡体以及湖相沉积物。根据湖相沉积物的年代测序,表明滑坡至少发生于2 600年前,现场调查滑坡内存在正断层其位置为云母片麻岩、斜长角闪岩的分界面。滑坡前缘在板状、千枚状、片状、劈理化等变质地层中可见小规模的倾倒变形,滑坡后缘可见滑坡滑动面擦痕,产状为NE∠34°～38°,沟底有F17惠远寺-勒吉普断裂穿过。

经过现场岩石点荷载试验和室内力学试验测定岩体的物理力学参数(如表1所示)。此外,该滑坡距离巴塘断裂仅48 km,靠近活动断裂且该区域内地震频发,未来仍可能发生M≥7.0 级的强震,发生崩塌滑坡的可能性较大。

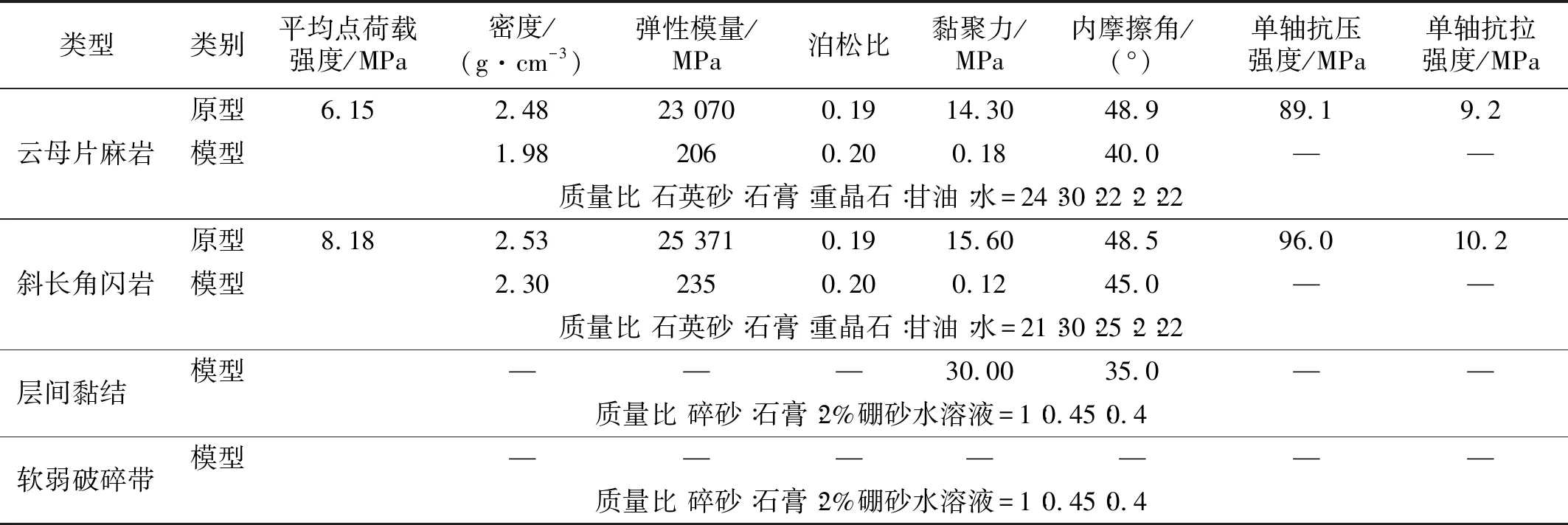
表1 原型与模型材料的主要物理力学参数

1.2 相似材料与模型设计

Cg=Ca=Cρ=Cφ=1,

Ct=(CL/Ca)1/2,

CL=CD=100,

Cc=CE=100,

(1)

式中,Cg,CL,Cρ,CE,CC,Cφ,Ca,CD,Ct,Cf分别为重力、几何尺寸、密度、弹性模量、黏聚力、内摩擦角、加速度、位移、时间、频率的相似系数。

本次振动台缩尺试验以地层结构和岩性作为主要的模拟内容,模型边坡的主要特征为:①模型长(160 cm)×宽(120 cm)×高(100 cm),并选取斜坡发生变形破坏区域为研究对象;②模型坡度与实际一致;③岩性一致,整体保持斜坡角度为45°;④薄层层状反倾岩质斜坡,岩层倾角为50°,并根据原型边坡中各层的厚度比例确定模型边坡中各层的厚度。在詹志发等[21]的研究基础上,由石英砂、石膏、重晶石、甘油和水五种材料制备成半径为25 mm,高度为100 mm的试样,石英砂为骨料,石膏起胶结作用,甘油起保水作用。在经过击实、烘干、脱模和养护等环节后成两种试验的相似材料单元板(长×宽为240 mm×120 mm,厚度分别为12 mm和9 mm)并测得试样物理参数(见表1)。 在采用单元板搭建物理模型模型时为了保证层面完整性,采用错缝搭接方式,各岩层接触面之间采用碎砂、石膏、2%硼砂水溶液按照一定的比例配制后,以薄层状(约2 mm)均匀地填充在岩层间。最后,在岩层表面覆盖一层薄层石膏砂浆抹面,保持表面光滑且平整。为减小模型箱效应的影响, 在模型边界和亚克力板之间放置10 cm厚的聚乙烯泡沫板,以减小模型箱对输入地震波的反射和折射(如图1所示)。

图1 搭建完成的斜坡模型

本次振动台模型试验中的传感器共包括加速度传感器(18个水平和4个竖向)、速度传感器(2个水平向)和坡表位移传感器(4个拉线4个激光),其中激光位移传感器测定斜坡水平向位移,拉线位移传感器测定斜坡竖向(沉降)位移,具体布置如图2所示。

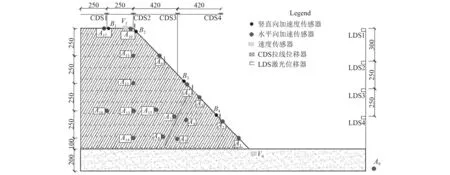
图2 各类传感器布置图(mm)

1.3 输入波的选取及加载顺序

为研究地震动参数和输入波类型对斜坡动力响应的影响,本次试验选取正弦波、汶川卧龙波、汶川茂县波、人工合成波作为输入波。每阶段输入波加载完成后采用白噪声进行扫频,以获得斜坡的动力特性,具体加载工况如表2所示。由于采集到的天然波中常混有其他噪声,且会存在基线飘零的现象,因此在对天然波进行基线校准,处理后的地震波时域图和频域图如图3、图4所示。

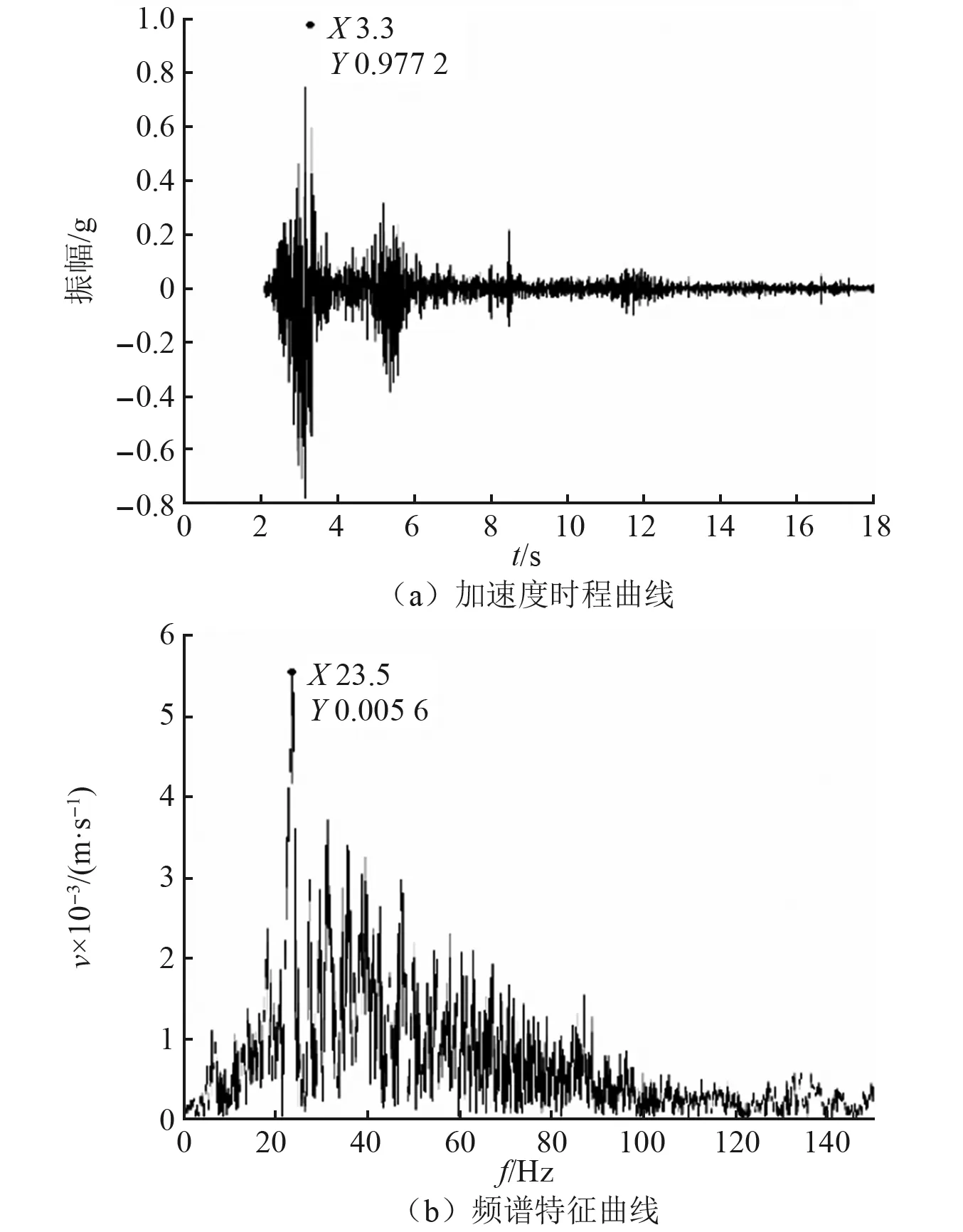
图3 汶川卧龙波

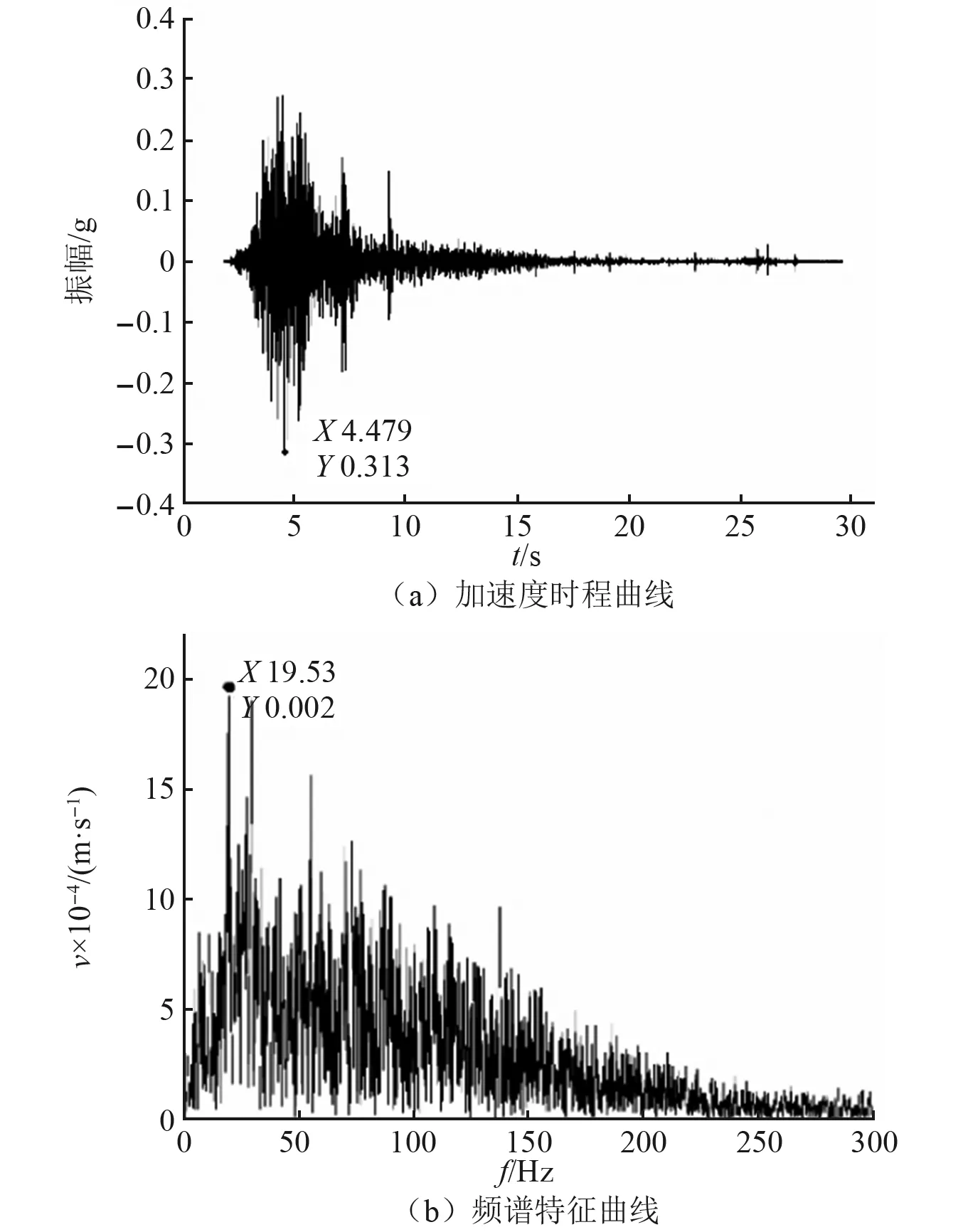
图4 汶川茂县波

表2 地震波加载工况

本次试验在北京工业大学结构试验大厅开展,试验数据采集对象主要包括加速度数据,速度数据和位移数据。通过IMC系统将电信号转换为加速度时程曲线,在不同工况地震波加载前加载白噪声,得到斜坡在当前条件下的动力特性。试验分为2个阶段:第一阶段为天然波,幅值从0.1g～0.5g方向为x方向击振,主要研究斜坡的动力响应特征;第二阶段为正弦波加载,频率从10 Hz～35 Hz,间隔5 Hz。最后,增加输入天然波的幅值,分析斜坡在地震作用下的破坏过程。加载完每一级振幅后,暂停试验10 min,记录比较斜坡变形情况,也为位移传感器记录斜坡的位移变化留下了足够的时间。

2 斜坡固有频率特征

本文基于试验过程中施加白噪声激励获取的斜坡内在动力相应规律,得到在不同工况地震波加载前白噪声的相对传递函数虚部曲线,试验过程中共进行11次白噪声,获取某一时刻的斜坡自振频率。斜坡的自振频率从初始值28.67 Hz(如图5(a)所示),经过各工况地震波加载完成后最终值为21.38 Hz(如图5(b)所示),降低7.29 Hz。

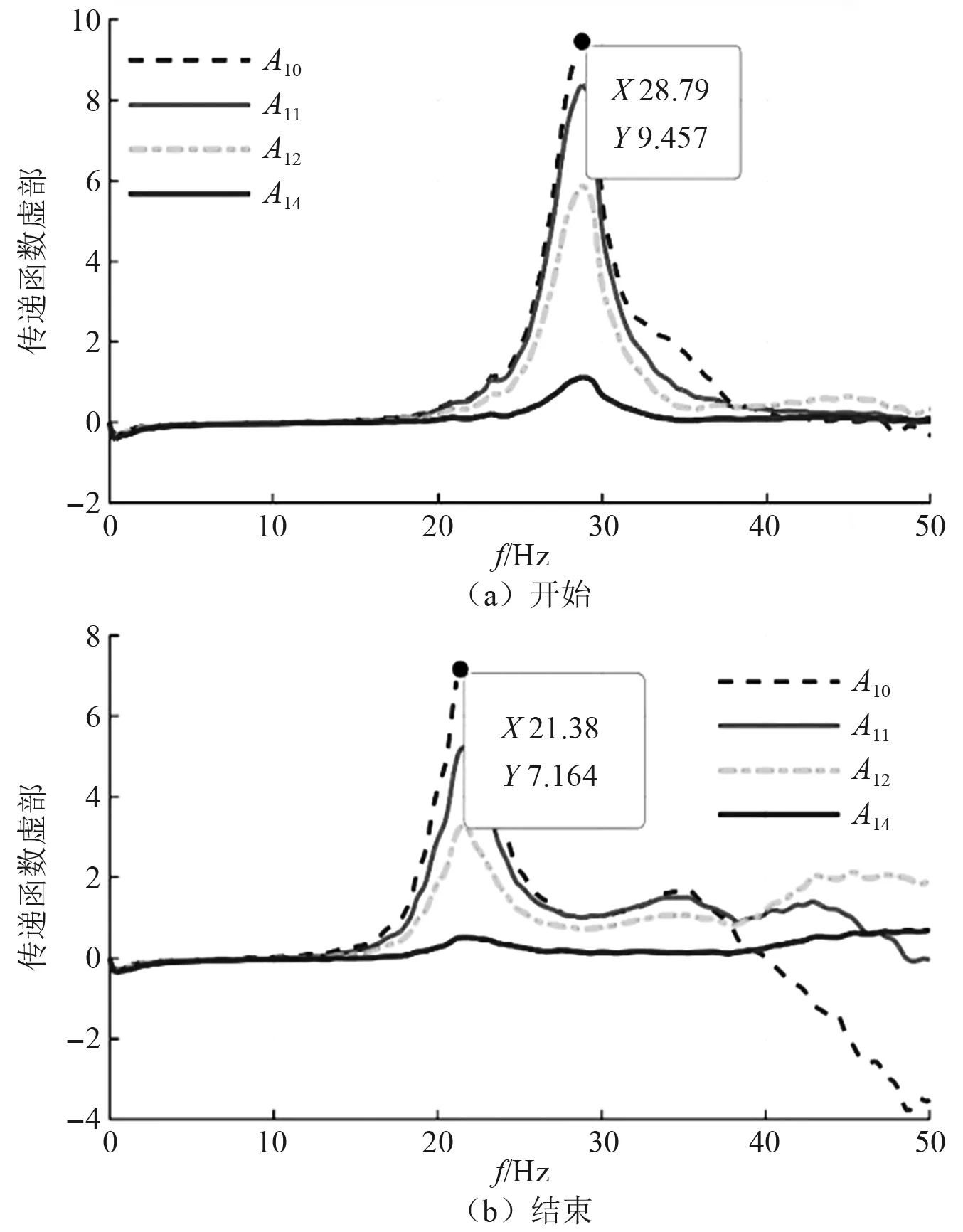
图5 斜坡自振频率变化图

随着输入波幅值的增加,斜坡的自振频率整体呈下降趋势,阻尼比呈上升趋势,曲线呈现出两次明显的线性变化阶段(如图6所示),其输入波幅值区间为0.4g～0.8g,斜坡自振频率下降,阻尼比上升明显,斜坡表面开裂和浅层的倾倒-滑移。输入波幅值超过0.8g,斜坡自振频率急剧下降,斜坡阻尼比先下降后上升,且斜坡大变形,出现塑性区发生大规模块状滑移-倾倒。同时在以往的试验中对于斜坡特性分析主要集中在自振频率上,对于阻尼比鲜少分析求解,在本次试验中表明阻尼比与自振频率呈现反相关关系,作为反应斜坡耗能指标的重要参数能直观的体现斜坡在动力作用下的特征。

按《水利水电工程地质勘察规范》（GB 50287—99）规定，饱和砂或饱和少黏性土的N63.5值小于按公式算出的液化临界击数Ncr时，可判为液化土。

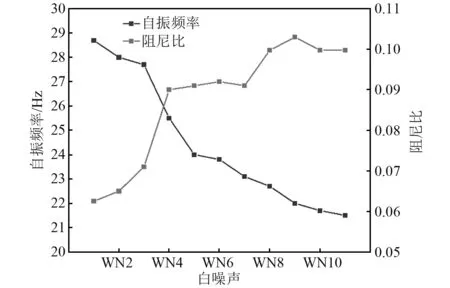
图6 各工况下斜坡自振频率及阻尼比

3 反倾岩质斜坡破坏过程分析

由不同幅值地震波作用下边坡的失稳破坏过程可以发现,0.3g是边坡启裂的临界动力条件,当输入地震动幅值大于0.3g时(如图7所示),边坡坡顶和坡中处产生大量张拉裂缝,坡脚处产生压剪裂缝,坡体表面块体碎裂化程度随着幅值的增加而增强,边坡由线性阶段进入到非线性阶段。0.7g～0.8g(如图8所示)为边坡破坏的临界动力条件,此时斜坡表面块体滑落,坡脚处压剪裂缝贯通并向上发展,坡顶处张拉裂缝向边坡内部发展,与下部压剪裂缝形成主滑面。

图7 岩层开裂-变形

图8 岩层浅层滑移-块状倾倒-失稳破坏图

斜坡整体发生块状倾倒破坏,强震作用下的含结构面反倾岩质斜坡破坏模式可以总结为3个主要阶段:坡顶张拉裂缝和坡脚剪切裂缝的形成→裂缝的扩展和浅层块体的剪切破坏滑动-结构面以下岩层块状倾倒→斜坡浅层的主滑面的形成。

当输入波幅值小于等于0.3g时,斜坡无明显位移。当输入波幅值大于等于0.3g时,坡趾及坡中处均发生竖向位移(如图9所示),其中坡顶发生显著沉降;水平位移在坡高1/3处为峰值。当幅值到达0.6g～0.7g时,斜坡水平位移增加了10 mm;斜坡坡顶竖向位移增量达到30 mm。试验加载工况结束后,竖向位移达到最值出现在坡肩处,与试验中观察到的斜坡早坡顶处发生了明显的下陷相符;水平位移最大值位置在1/3坡高处,整体斜坡变形过程从坡顶开始,1/3坡高处以下变形破坏最为强烈,坡顶下沉严重,结构面的存在对于斜坡受动力影响巨大,结构面以下岩层呈现滑移-块状倾倒现象。

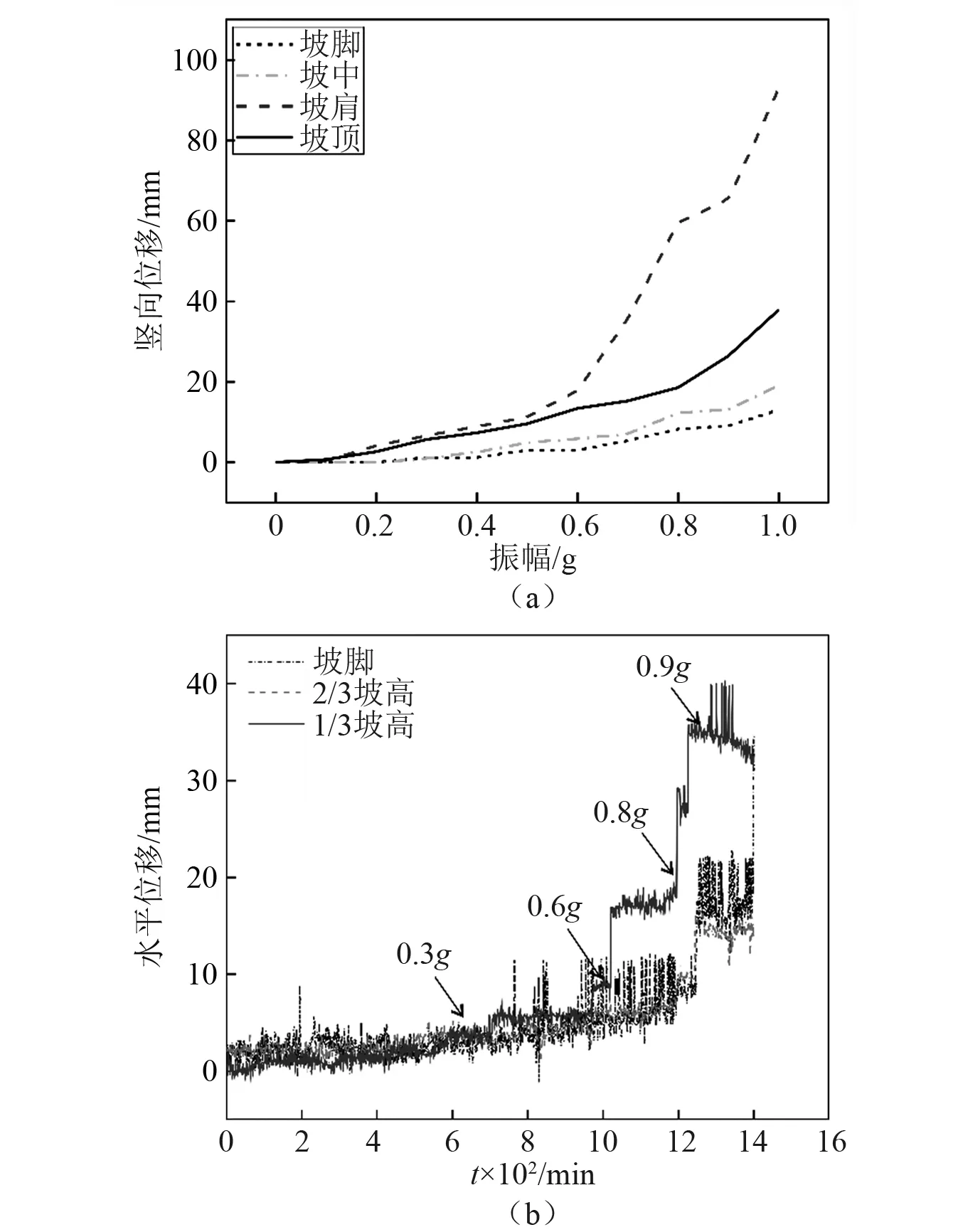
图9 斜坡表面不同位置水平与竖向位移图

4 反倾岩质斜坡动力响应规律

由于斜坡自身存在阻尼,对于地震波有吸收作用,具体体现为高频波过滤,低频波放大,用峰值地面加速度(peak ground acceleration,PGA)放大系数反映各监测点的峰值加速度与振动台台面监测点的峰值加速度之比,直观体现斜坡不同位置对于动力响应的强弱关系[22]。选取幅值为0.2g和0.6g茂县波作为动力输入条件,研究线性阶段和非线性阶段斜坡动力响应规律。根据加速度传感器的监测结果,做出不同幅值下斜坡的PGA等值线图(如图10所示)。在 0.2g茂县波作用下,斜坡具有明显的“高程放大效应”,加速度放大系数在坡顶处达到峰值;在加载0.6g茂县波时,高程放大效应扩散的范围更广,在坡中处呈现急剧增的趋势。斜坡加速度放大系数沿水平方向表现出节律性的变化,表现为越趋于坡表,加速度放大系数越大,且随着幅值和高程的增加,“趋表效应”越明显。

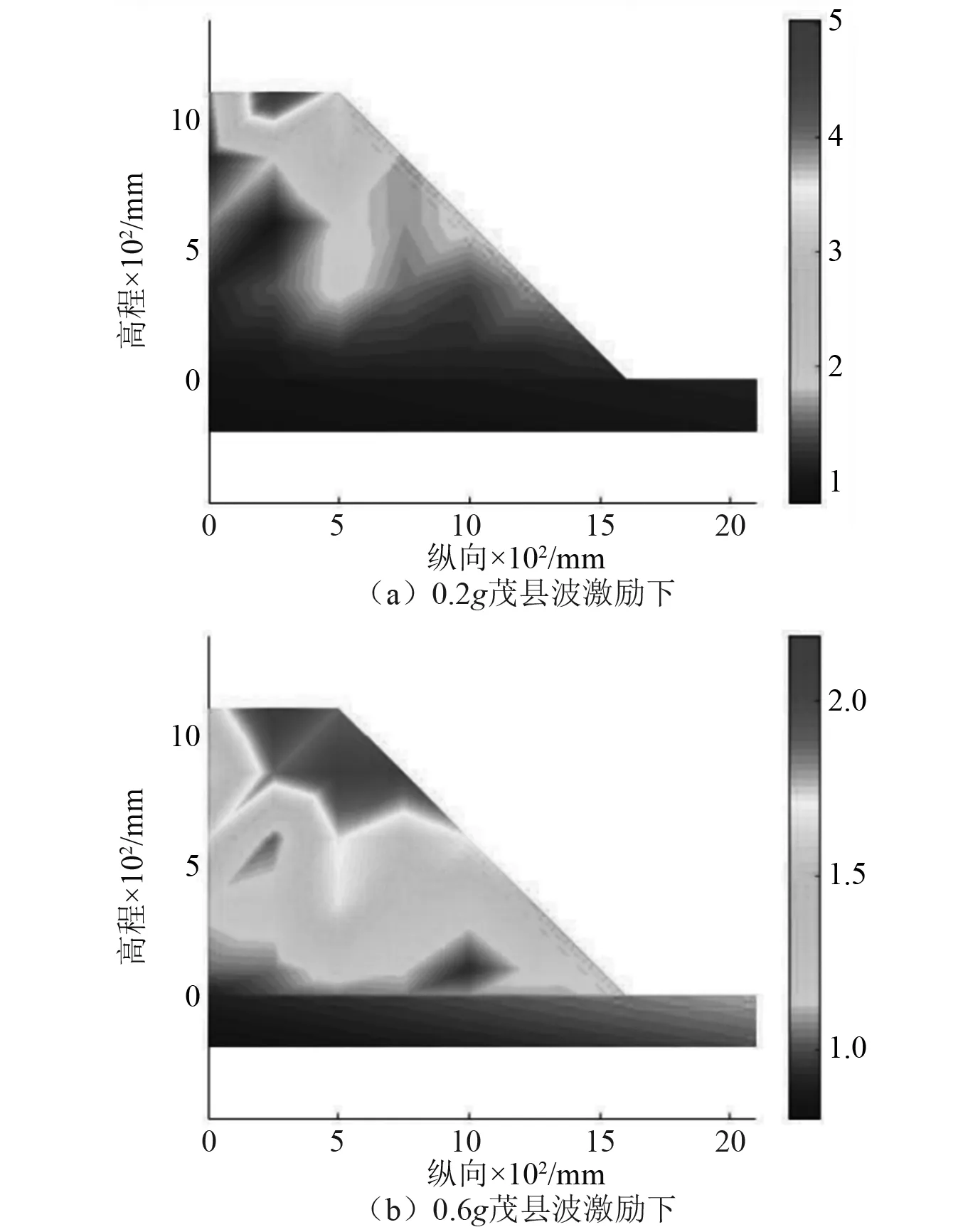
图10 不同幅值下斜坡加速度放大系数等值线云图

斜坡加速度放大系数在不同幅值地震波作用下随高程的变化趋势,如图11所示。在0.2g茂县波作用下,斜坡加速度放大系数的峰值出现在坡顶位置;在0.6g茂县波作用下,高程放大效应范围更广,在坡高1/2以上处呈现急剧增的趋势。斜坡加速度放大系数沿水平方向表现出规律性的变化,表现为越靠近坡表,斜坡的加速度放大系数越大。

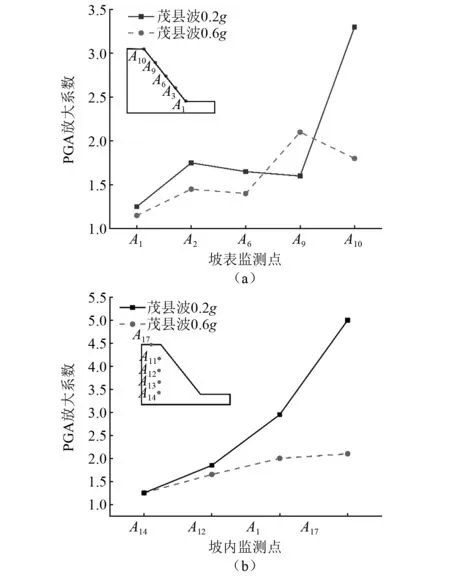
图11 不同幅值下坡表和坡内加速度放大系数曲线

4.1 输入波频率的影响

图12为0.3g正弦波作用下不同频率的坡面和坡内加速度放大系数变化规律。加速度放大系数随着输入频率的增大呈现先增大后减小的趋势,当正弦波输入频率小于20 Hz时,边坡表面和坡体内部的加速度放大系数随输入频率的增大而增大。当输入频率超过20 Hz时,加速度放大系数随输入频率的增大而减小,并且这种现象随着坡高的增加而愈加明显。坡趾处的加速度放大系数随输入频率的增加变化不明显;在某些情况下,甚至会削弱地震波的放大效应。

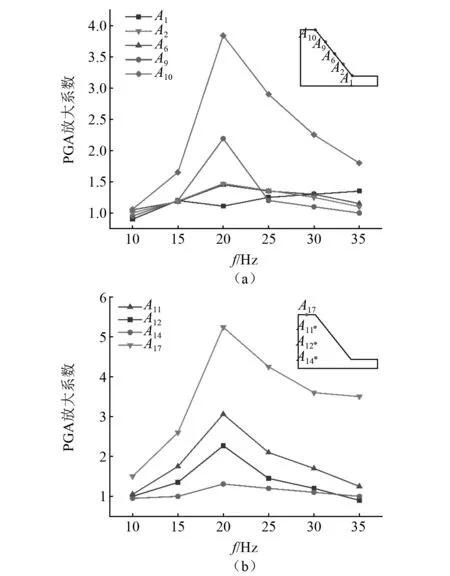
图12 正弦波0.3g幅值下斜坡加速度 放大系数随频率变化图

图13为0.3g幅值正弦波作用下不同频率的加速度放大系数随高程的变化趋势。在不同频率的正弦波作用下,坡面加速度放大系数随高程的增加呈非线性增大;对于不同频率的输入波,斜坡加速度放大系数的出现拐点位置也明显不同。频率20 Hz的正弦波,加速度放大系数在坡高1/2处急剧增大,而对于其他频率,加速度放大系数在坡高3/4处急剧增大,呈现出相似的特性。坡体内部加速度放大系数随高程增加基本呈线性增长趋势,在不同频率正弦波作用下增长速率不同,放大系数增长速率拐点出现在边坡自振频率附近。

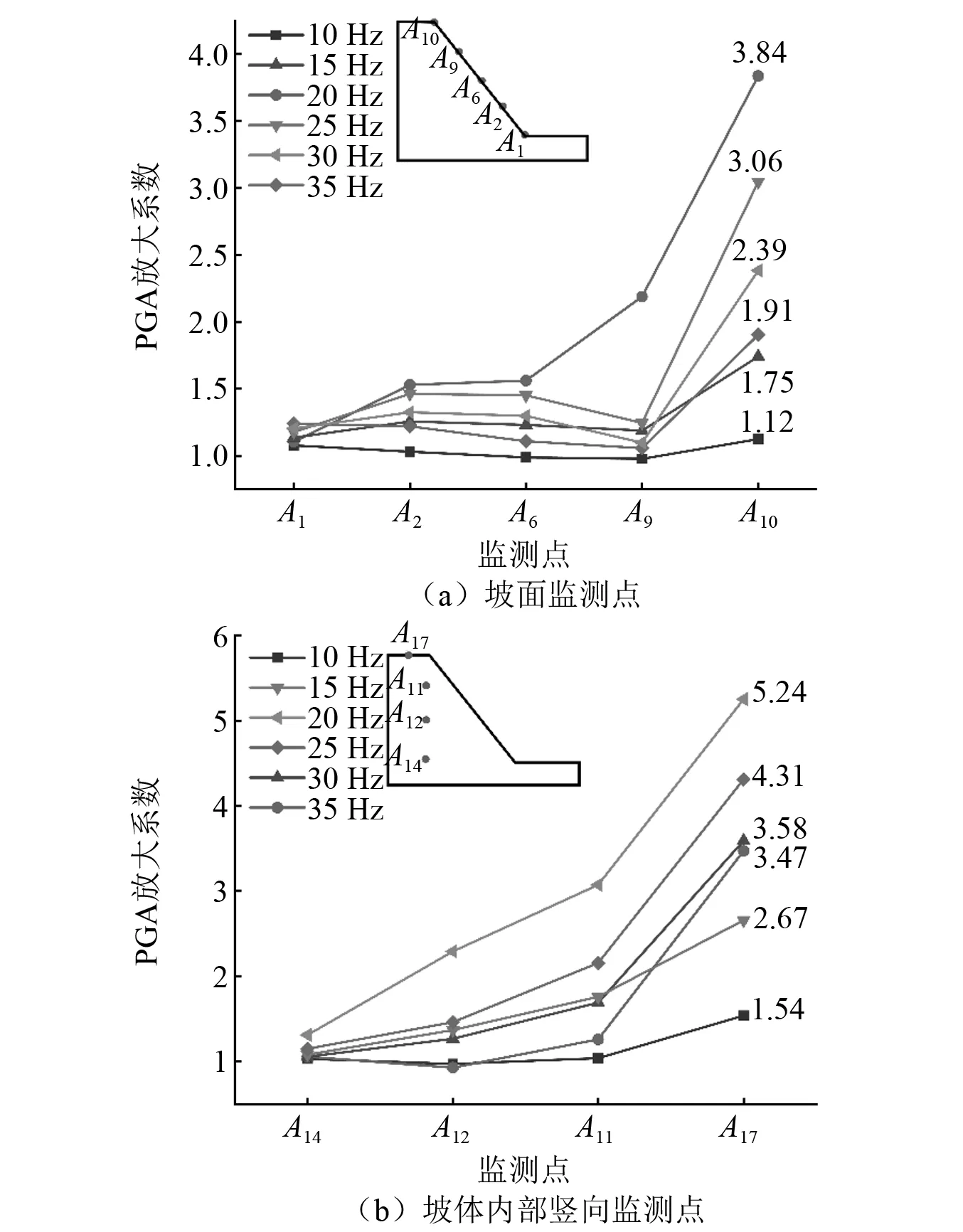
图13 不同频率下加速度放大系数随高程变化

4.2 输入波幅值影响

由图14可知,坡面加速度放大系数随着幅值的增大先增大后减小,当输入地震动幅值小于0.3g时,坡面加速度放大系数随着幅值的增大而增大。当输入地震波的幅值超过0.3g时,PGA随着输入幅值的增大而减小,并且在0.3g时达到峰值。与刘汉香等反倾斜坡振动台试验得到的幅值对斜坡动力响应特征的总体趋势相符,即斜面加速度放大系数随着幅值的增加呈现先增加后减小的趋势,但在本次试验中放大系数最大值对应的幅值高于原结论(0.2g)。坡内加速度放大系数变化规律坡表趋势相同,也存在先增大后减小的现象,在输入正弦波振幅为0.3g时达到峰值。

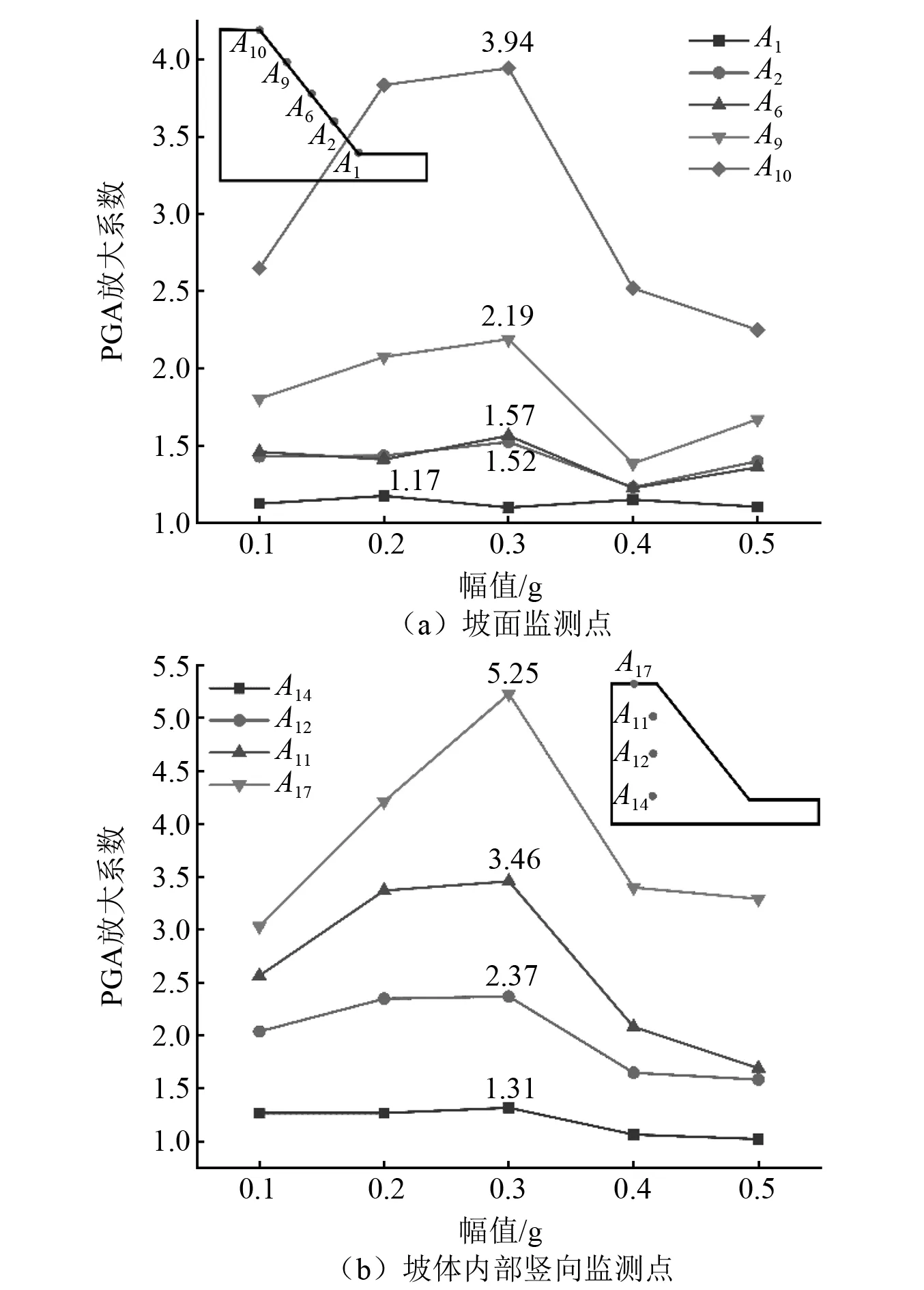
图14 不同幅值下的加速度放大系数

图15为不同幅值正弦波作用下边坡加速度放大系数随高程的变化图,坡面加速度放大系数随高程的增加并非呈线性增大趋势。当正弦波振幅小于0.3g时,在1/2坡高以下PGA缓慢增长,在1/2坡高处为拐点,PGA急剧增大,在坡顶处达到最大值。当正弦波振幅大于0.3g时,加速度放大系数在坡高3/4处显著增大。加速度放大系数沿坡体内部竖直方向呈线性增长,幅值变化对加速度放大系数增长速率影响不大。

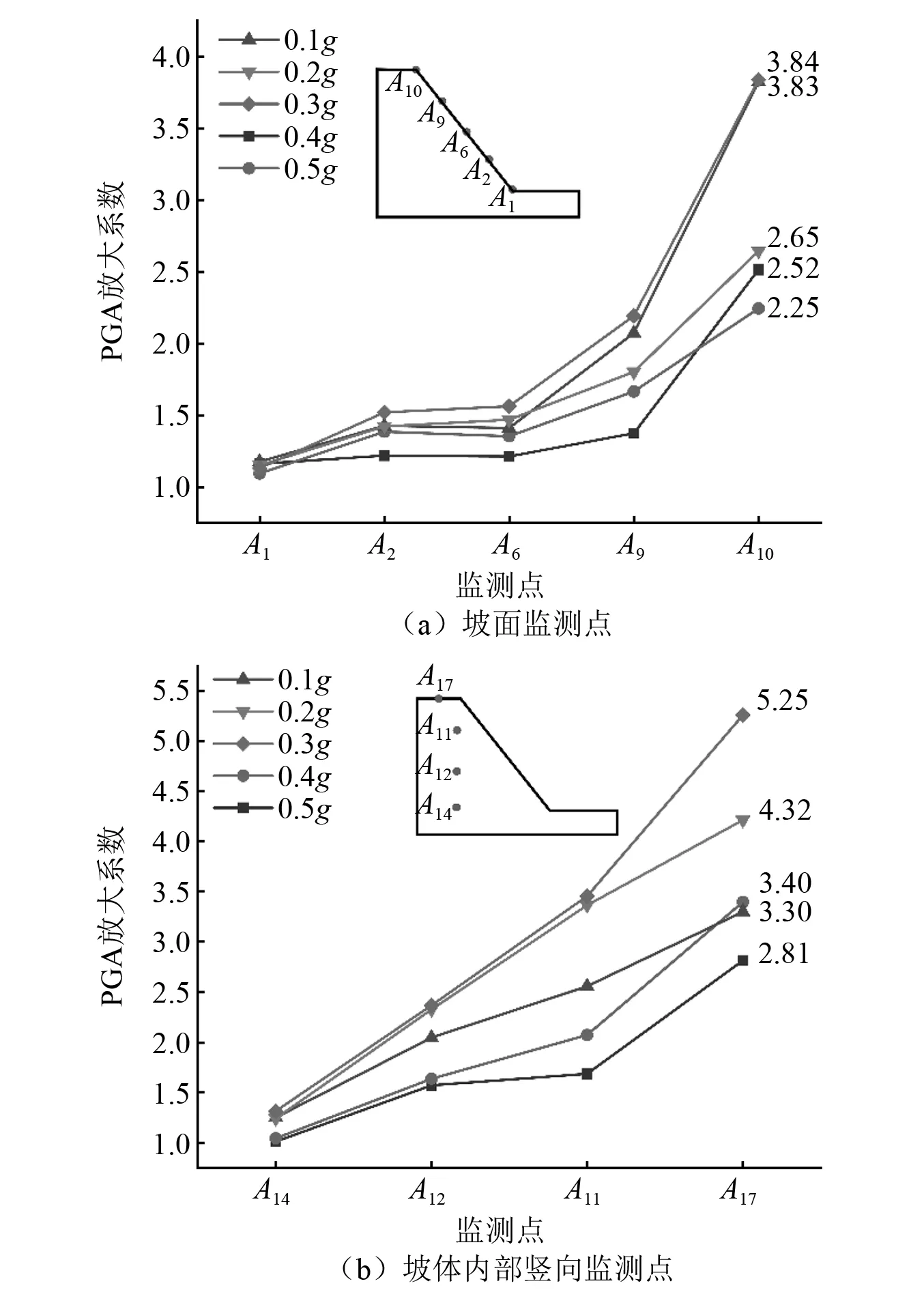
图15 加速度放大系数在不同幅值下随高程变化

基于以上对边坡动力响应的分析,频率和幅值共同影响边坡动力响应,控制坡面加速度放大系数以及出现拐点的位置。当输入波接近边坡自振频率或波幅小于0.3g时,坡面加速度放大系数在坡面中部开始急剧增大。当输入波频率高于或低于边坡自振频率或幅值大于0.3g时,坡面加速度放大系数的增长拐点都出现在坡高3/4处。坡体内部竖向加速度放大系数的增大趋势受频率和幅值的影响较小;但输入波频率对加速度放大系数增长率的影响高于幅值。当输入波频率越接近边坡自振频率时,加速度放大系数曲线增长速率越快。

4.3 输入波类型的影响

地震波作为一种随机波,频谱成分复杂,因而其对边坡的影响也不尽相同。本研究以茂县基岩地震波、卧龙土层地震波、基于研究区合成波、正弦波作为动力输入条件,分析了不同地震波类型下斜坡动力响应特征。斜坡对不同类型地震波的放大效应差别较大(如图16所示),对于坡面监测点(除坡肩处),天然波的坡面动力放大效应均高于正弦波和合成波,茂县基岩波的坡面动力放大效应更大。斜坡对合成波的放大作用不明显,在正弦激励下,坡顶对地震波的放大效应最大。对于随着高程的增加,坡内对正弦波的放大作用逐渐增强,造成这种现象的原因可能与输入的固有频率和频带有关,前文所述茂县基岩波的卓越频率为19.3 Hz,卓越频段在19.3 Hz～80 Hz,低于斜坡的自振频率,且频段宽度较宽,导致振动过程中斜坡产生的能量越大,因此斜坡的放大效应越强;汶川卧龙波的卓越频频率虽然接近边坡自振频率且谱值较茂县波高,但是频带宽度较窄,导致斜坡的放大作用并不明显。因此关于岩质斜坡的动力研究,输入地震波选取基岩地震波较为合适。

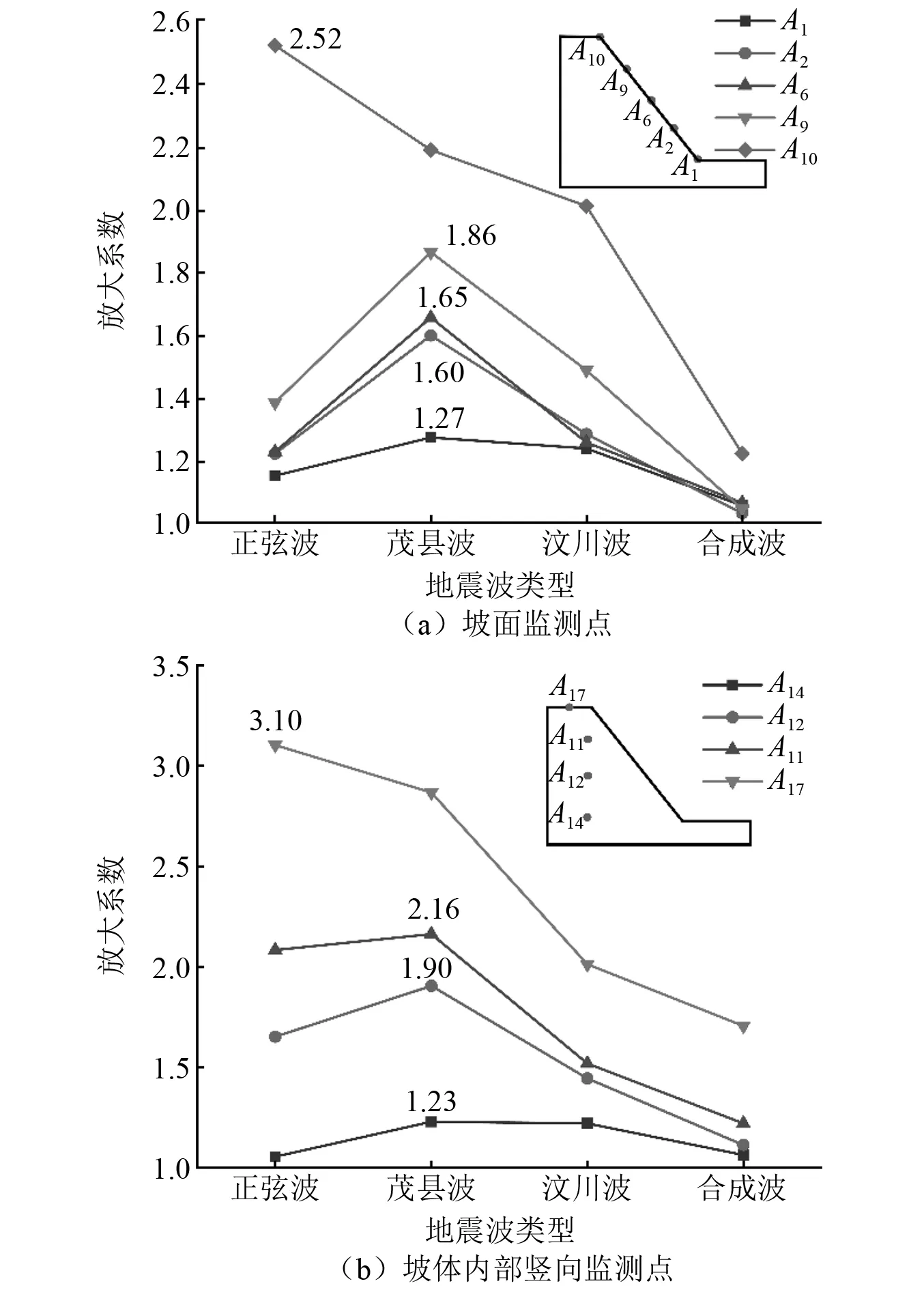
图16 不同地震波类型下的加速度放大系数

4.4 结构面的影响

软弱破碎带的存在对斜坡的动力响应有显著的影响,本文在结合实际断层的基础上采用下薄上厚的楔形状结构面。同时在软弱夹层上下各布置3个加速度传感器,用来研究结构面对反倾岩质斜坡的动力响应的影响和对输入地震波的影响,其中上层加速度传感为A6,A7,A8,下部传感器为A3,A4,A5。试验分析结果如图17所示。

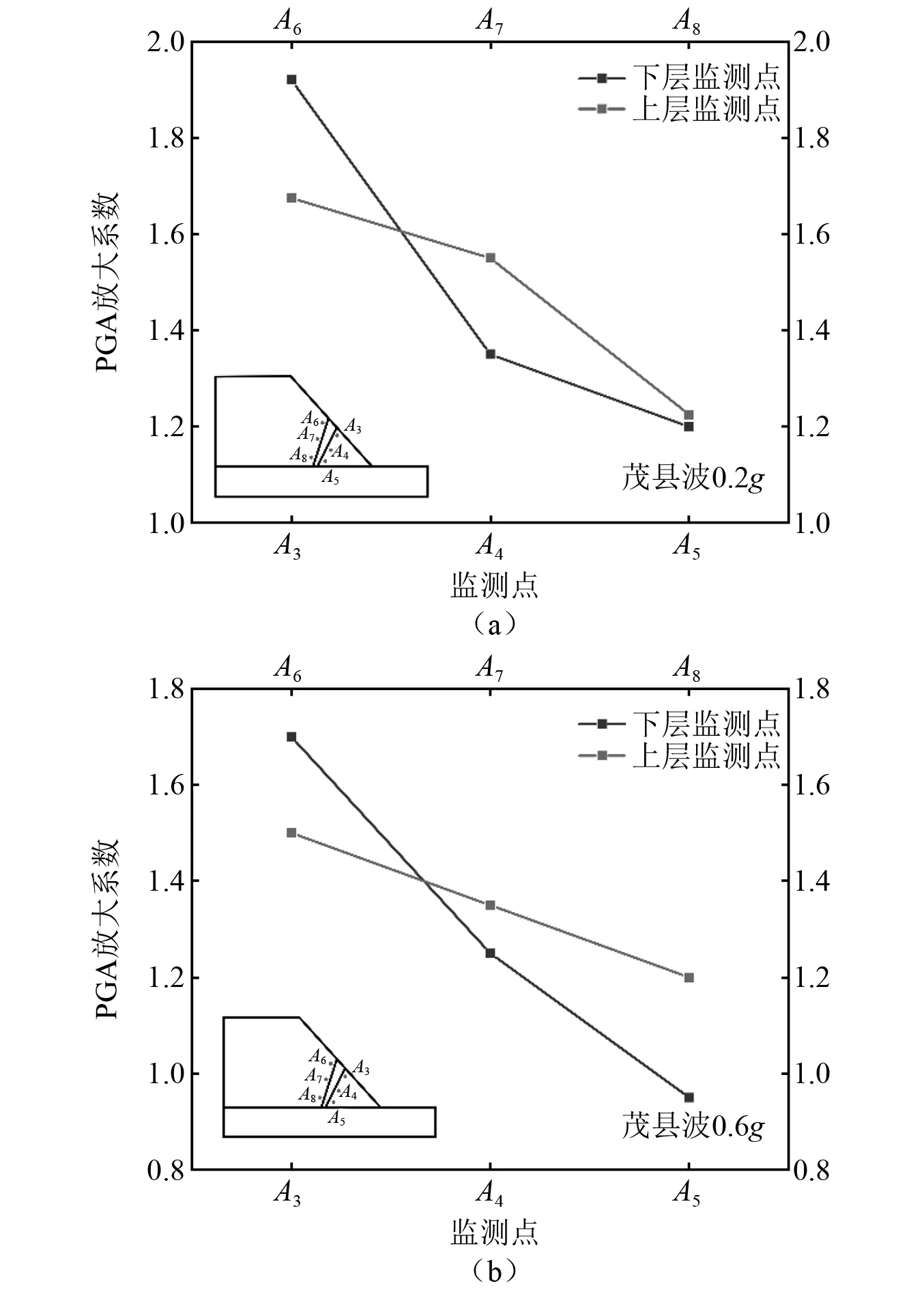
图17 不同幅值下结构面上下层放大系数

试验中设置的软弱破碎带厚度不一致,导致不同位置放大效应不同。当地震波幅值较低,坡底处软弱破碎带对地震波的放大作用不明显;随着高程增大,监测点A6～A8的PGA体现出先大后小的现象,即地震波经过结构面中部时放大效应明显,趋于坡表体现为抑制放大效应。当输入地震波的幅值为0.6g时,结构面下层的放大作用明显增强,结构面中部的放大效应较低幅值地震波作用更弱。傅里叶谱反映了输入地震波在频域内的特性,实现了地震波从时域分析到频域分析的转换,可以清晰的看出各频段内的地震动响应程度和振动能量在各频率范围内的分布情况,进而对地震波在斜坡的传播过程进行深入的研究。为了更加直观的分析软弱破碎带对输入地震波的影响和对斜坡动力响应的影响,采用快速傅里叶变换得到 0.2g茂县波和0.6g茂县波作用下,软弱夹层两侧测点傅氏图,如图18所示。

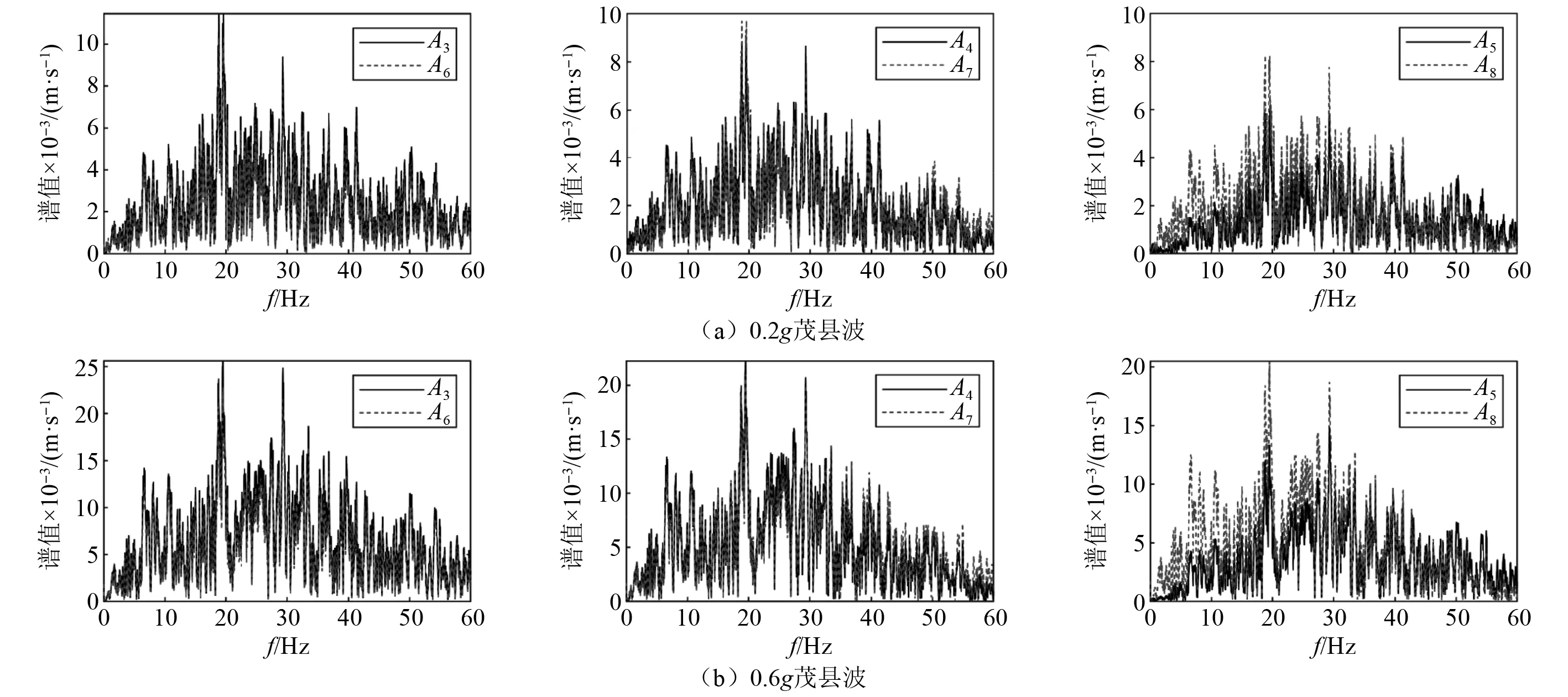
图18 不同幅值结构面上下测点傅里叶谱图

由于软弱破碎带厚度不一致,导致地震波频段在穿越不同位置软弱破碎带时发生的改变也不尽相同。坡底软弱破碎带较薄,地震波由下层监测点到上层监测点,8 Hz～21 Hz频段发生了明显的放大作用;对于软弱破碎带中部监测点,地震波经过软弱破碎带,在20 Hz～25 Hz 频段内有所放大;对于接近坡表的监测点,软弱破碎带的存在抑制了斜坡对地震波的放大作用。由以上分析可以看出,不同厚度软弱破碎带对地震波在斜坡内的传播影响不同,软弱破碎带厚度较薄时,对输入的地震波起到放大作用,随着软弱夹层厚度的增加,这种放大效应逐渐减弱,当超过某一厚度时,会抑制斜坡对地震波的放大作用。产生该现象的原因是由于软弱破碎带较薄时,地震波在软弱破碎带上层和下层发生反射和折射,增强了地震波的能量。

5 结 论

本文采用北京工业大学西区结构试验大厅3 m×3 m的振动台,以宗绒滑坡为试验原型,建立了几何相似比为1∶100的缩尺反倾岩质斜坡模型,开展了大型振动台模型试验,研究了强震作用下反倾岩质斜坡的动力学响应规律,分析了斜坡的启裂和失稳临界动力条件。得到以下结论:

(1)随着输入波次数的增加,斜坡自振频率逐渐降低,在0.3g输入波加载后,斜坡进入了非线性阶段。强震作用下斜坡对地震波产生明显的高程放大效应和趋表效应,且幅值越大,现象越明显,斜坡的动力放大效应的分布范围与幅值正相关。

(2)低幅值作用下,斜坡加速放大系数在输入波频率接近斜坡自振频率时达到最值;高幅值作用下,斜坡加速度放大系数最大值出现在低于斜坡自振频率附近。同时加速度放大系数增长速率受频率的影响更大,越接近斜坡的固有频率,加速度放大系数曲线上升的越快。

(3)软弱破碎带的存在对斜坡动力响应和稳定性具有很大的影响,其厚度对放大效应存在明显的差异,整体上表现为厚层段抑制,薄层段放大。幅值0.3g～0.4g是斜坡启裂的临界动力条件,0.7g～0.8g是斜坡失稳破坏的临界动力条件。