卫生型快开人孔整体有限元模型及钩锁强度分析

卢海山* 龚曙光 沈 壮 唐 芳

（湘潭大学 机械工程与力学学院）

0 引言

卫生型快开人孔装置因具有开闭顶盖便捷，无死角、易于清洗等优点，近年来被广泛应用在医药、食品等行业中具有高洁净要求的压力设备，如各类发酵罐、配液罐等[1]。目前尚无此类人孔的设计标准，仅有温州工业设计院编制的QBJ—B01.01～01.07—2013《卫生型 快开人、手孔》可用于参考[2]。设计人员通常依据经验进行设计，尽管多数情况下能满足使用要求，但在罐体压力试验或实际运行中，常出现人孔法兰泄漏现象[3]。同时，文献[3]指出人孔法兰泄漏的主要原因是钩锁结构不合理导致强度不足。

随着有限元方法和分析设计的普遍应用，设计人员基于单一的部件模型开展了各类快开结构的应力分析[4]与优化设计[5-6]。然而尽管文献[7]表明采用单一的部件模型可对快开法兰进行强度评定，但是难以对该文所述卫生型快开人孔中的钩锁等结构进行准确的应力分析，因此有必要考虑各部件的接触关系建立整体有限元模型进行结构分析，避免计算部件之间的相互作用载荷[8-9]。本文将建立人孔的三维整体有限元模型，分析人孔的强度并为人孔设计提供指导。

1 结构描述

某制药用压力容器的设计压力为0.4 MPa，设计温度为146 ℃。人孔安装于容器顶部的封头，人孔的规格为DN400 mm，其结构如图1 所示。

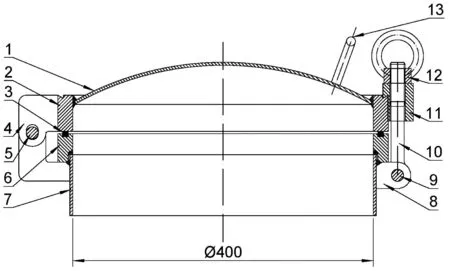
图1 快开人孔结构示意图（单位：mm）

人孔的球冠形封头与上法兰焊接组成人孔的顶盖，且顶盖可绕销轴转动开启或关闭。人孔的下法兰与筒节焊接，且筒节底部焊接在容器顶部的封头。沿人孔的上、下法兰圆周方向均布8 只钩锁，通过拧紧环形螺母使钩锁压紧上、下法兰及二者之间的O型圈，从而实现人孔密封效果。钩锁的结构如图2 所示，其缺口角度为α。

图2 钩锁结构示意图

2 整体有限元模型

2.1 分析模型

为了准确分析人孔各部件的强度，以整体人孔装置为计算对象，仅忽略对结构强度影响甚微的耳板、销轴和把手，建立人孔的整体模型，如图3 a）所示。由图3 a）可知，该整体模型具有对称性，可沿周向取人孔整体结构的1/8 进行分析，如图3 b）所示，从而减小有限元计算量。图3 b）中的模型包括球冠形封头、上法兰、O 型圈、下法兰、筒节、活节螺栓耳板、活节螺栓销轴、活节螺栓、环形螺母和钩锁等部件，其中，以焊接相连的部件在建模时作为整体部件。如球冠形封头与上法兰，下法兰与筒节及活节螺栓耳板。此外，为了简化模型，将环形螺母与活节螺栓也作为整体部件，其余部件之间均处理为接触关系。

图3 实体模型

选取节点自由度为UX、UY和UZ的八节点六面体单元为网格划分类型，并采用映射方式将所有三维实体划分为六面体规整网格。得到的网格模型如图4所示，网格模型的节点总数为2 288 013，单元总数为1 177 231。同时，为了模拟环形螺母拧紧时活节螺栓的预紧载荷，在活节螺栓的中间位置建立了预紧单元。

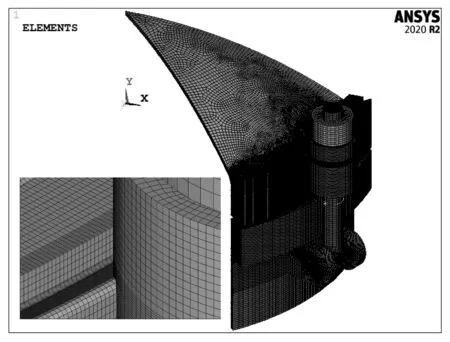
图4 网格模型

在处理为接触关系的部件之间利用目标和接触单元定义接触对，模拟部件之间的实际接触状态，包括上法兰与O 型圈、下法兰与O 型圈、环形螺母与钩锁、钩锁与上法兰、活节螺栓与活节螺栓销轴以及活节螺栓销轴与活节螺栓耳板，如图5 所示。

图5 模型接触对示意图

2.2 材料参数

直接与介质接触的金属部件，即球冠形封头、上法兰、下法兰和筒节的材质为S31603 不锈钢，其余非直接接触介质的部件，包括环形螺母、钩锁、活节螺栓、活节螺栓销轴以及活节螺栓耳板等，其材质为S30408 不锈钢。在整体有限元模型中，S31603 和S30408 材料可采用线弹性模型进行模拟，仅需定义弹性模量与泊松比即可。O 型圈的材质为硅橡胶，为超弹性材料，采用2 阶的Mooney-Revlin 模型进行模拟[10]，其表达式为：

式中：W——应变势能函数；

I1，I2——分别为第1 和第2 应变不变量；

c10，c01——分别为S31603 和S30408 材料常数；

d——材料不可压缩参数；

J——弹性体变形梯度的确定参数。

此外，在接触对的模拟中需设置不锈钢与不锈钢、不锈钢与硅橡胶之间的摩擦系数。各类材料参数如表1 所示。

表1 材料参数

2.3 约束与载荷

图6 为模型约束及载荷示意图。由于取人孔整体结构的1/8 作为分析模型，因此在模型两侧的剖切面施加对称约束，同时限制底部端面的轴向位移为0。由于考虑预紧载荷与内压的共同作用，因此在活节螺栓中间位置的预紧单元处施加轴向压缩位移0.5 mm，模拟预紧载荷，并在模型内壁面施加设计压力0.4 MPa。显然，该方法考虑了各部件的接触关系建立人孔的三维非线性整体有限元模型，从而避免了采用单一部件模型分析结构强度时，面临各部件之间相互作用载荷难以准确计算的问题。

图6 约束及载荷的示意图

2.4 求解设置

采用Newton-Raphson 方法，分为2 个载荷步求解整体有限元模型，其中载荷步1 获得预紧载荷下的结构响应，载荷步2 获得预紧载荷和内压共同作用下的结构响应。由于O 型圈的材质属于超弹性材料，因此开启程序中的大变形开关，以捕捉可能产生的大应变。在求解过程中，由程序自动选择载荷增量的步长，以在保证计算精度的前提下提高收敛速度，同时开启程序中的预测器和线性搜索，以进一步加快非线性求解的收敛速度。

3 结果分析及讨论

3.1 结果分析

图7 为α=60°时人孔的应力强度分布情况。由图7 可知，人孔各部件的应力强度值较低。定义应力线性化的路径，如图8 所示，分别为路径A～H。应力线性化及评定结果如表2 所示。由图7 和表2 可知，球冠形封头、上法兰、下法兰、筒节、活节螺栓销轴与活节螺栓耳板等部件的强度均满足要求。

表2 沿路径的应力评定

图7 人孔的应力强度分布情况（单位：MPa）

图8 应力评定路径示意图

由图7 e）可知，钩锁为主要承压元件，其局部位置的应力强度值较大，且最大应力强度位于钩锁的缺口根部，最大值为415.1 MPa。显然该最大应力强度值已经超出了S30408 的屈服极限，因此在实际使用过程中，钩锁的局部位置较易发生塑性变形。

3.2 讨论

由于不同缺口角度下钩锁受到的载荷大小不同，因此有必要分析缺口角度对钩锁应力强度的影响。图9 为不同缺口角度下钩锁的应力强度分布云图。由图9 可知，在不同缺口角度的情况下，钩锁的应力强度分布形式一致，其最大值均位于钩锁缺口根部的外侧，且随着缺口角度减小，其最大值的覆盖范围沿缺口根部向钩锁内侧扩展。

图9 不同缺口角度下的钩锁应力强度分布情况（单位：MPa）

图10 为不同缺口角度下的螺栓力和最大应力强度值。由图10 a）可知，不同缺口角度下的螺栓力基本一致，因为不同缺口角度下人孔顶盖所承受的内压是相等的，即上、下法兰之间所需要的压紧力基本一致，因此轴向方向上的螺栓力基本一致。然而随着缺口角度减小，钩锁的最大应力强度值急剧增大，如图10 b）所示。这是因为钩锁与上法兰之间接触斜面上法向接触力的轴向分力提供上、下法兰之间的压紧力，而上、下法兰之间的压紧力基本一致，则缺口角度越小，钩锁承受的载荷越大，从而导致钩锁的最大应力强度值越大。因此采用较大的缺口角度有利于降低钩锁的局部应力强度。

图10 不同缺口角度下的螺栓力与钩锁最大应力强度

4 结语

（1）考虑部件的接触关系，建立了含超弹性密封圈的人孔三维非线性整体有限元模型，得到了预紧力和内压共同作用下的人孔应力强度,避免了采用单一部件模型分析部件强度时载荷难以准确计算的问题。

（2）人孔各主要受压元件的应力强度值较低，满足强度要求，但钩锁的缺口根部存在严重的应力集中情况，若结构设计不合理，则钩锁容易出现强度不足，从而导致人孔法兰泄漏失效的风险。

（3）钩锁的缺口角度越大，钩锁的最大应力强度值越小，建议采用较大的缺口角度，以改善钩锁缺口根部的应力集中情况。