高速磁浮列车长定子直线同步电机铁耗分析

马金虎, 卢琴芬, 李焱鑫

(浙江大学电气工程学院, 浙江 杭州 310027)

1 引言

高速磁浮列车作为21世纪交通高速化领域的研究热点,不仅能够达到比轮轨交通更高的运行速度,而且具有启动速度更快、环境污染更小、维护成本更低以及更明显的经济、能源等方面的诸多优势[1-3]。我国一直重视高速磁浮列车的应用,近年来,高速磁浮成套技术和工程化能力不断提升。

高速磁浮列车牵引和悬浮系统的重要部件是长定子直线同步电机(Long-stator Linear Synchronous Motor, LLSM)。与普通电机相同,LLSM的损耗主要为绕组铜耗和铁心损耗(铁耗)[4,5]。铁耗与运行频率(运行速度)紧密相关,故准确计算并分析其影响因素对系统高速运行性能十分必要。

电机铁耗的计算和分析方法已有较多的研究。在结合已有计算模型研究方面,文献[6]利用分段变系数铁耗模型获得了变频供电的感应电机在多种运行条件下转子铁耗变化特性;文献[7]通过修正传统的Steinmetz损耗计算公式,对非正弦激励下的铁心材料非晶合金的损耗特性进行了计算和测量;文献[8]通过求解电机使用的硅钢叠片横截面积中磁扩散方程和使用静态磁滞Preisach模型表示磁化定律来计算硅钢片中的磁通密度和损耗变化,与使用非磁滞定律相比,这种计算方法精确度更高;文献[9]提出了一种基于直流偏磁特性和视在频率的具有小回路的一般磁滞回线的铁耗计算方法,适用于磁通密度波形中含有高次谐波的情况;文献[10]提出了一种应用于感应电机的铁耗预测改进方法,将铁心中的磁场分布与通用正弦磁通密度波形下叠片的功率损耗分析评估相关联,并对一台7.5 kW的四极电机进行了测试,结果表明改进的方法具有更高的精准度;文献[11]基于经典Steinmetz方程和频率分离方法,对比分析了高密度集中绕组内置式的永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)在三种不同磁体形状和不同转子拓扑结构下的铁耗;文献[12]提出了一种可以在正弦电源以及变频供电时对感应电机铁耗进行计算的方法;文献[13]提出修正延伸到矩形波激励计算的Steinmetz公式和在非正弦激励下的铁耗分离方法,对纳米晶铁心损耗进行了计算;文献[14]通过建立场路耦合模型来分析电机损耗和探究脉宽调制(Pulse Width Modulation, PWM)供电频率对永磁电机转子的损耗和温升情况;文献[15]改进了现有多环等效模型计算方法,构建了轴向磁通非晶合金电机空载铁耗的解析计算模型,分析了槽口和气隙长度对铁耗的影响;文献[16]提出一种计及铁耗、铜耗以及永磁体损耗的混合励磁电机建模方法,比传统模型计算精度更高;文献[17]基于铁耗分立计算模型提出了考虑温度、应力等多重物理因素下的高速PMSM的铁耗模型,通过试验对比,验证了模型的正确性;文献[18]利用开关磁阻电机(Switched Reluctance Motor, SRM)的磁动势和气隙磁导模型计算了其各部分的磁通密度,然后通过修正的Steinmetz模型来估算SRM铁耗。

在基于有限元方法进行计算方面,文献[19]利用有限元法通过在理想输入电流中注入与逆变器开关频率相同阶次的谐波,来计算牵引电机损耗,并与实际损耗相对比;文献[20]基于有限元方法研究了低速运行下的PMSM的负载变化对其转矩脉动和铁心损耗的影响,得出了铁心损耗的变化规律;文献[21]利用有限元法和铁耗分立计算模型,对一台5 kW的PMSM的空载铁耗分布特性进行了分析计算,通过对比试验,验证了计算的正确性;文献[22]采用有限元法对双边初级永磁型游标直线电机在不同参数下的推力和铁耗进行了分析,与实际试验结果一致,验证了分析方法的有效性。从上述文献和学者的研究中可以看出,目前对电机的铁耗计算多是先通过磁场分析,然后利用现有的计算模型来进行计算,其中铁耗分立计算模型应用较为广泛,但研究对象多集中于单一叠片或旋转电机,对直线电机的研究很少。对于高速磁浮列车LLSM的铁耗,高速运行下包含谐波的铁耗测试很难完成,因此本文基于有限元方法计算并分析,这也是电机铁耗分析常用的分析方法。

本文首先基于三种有限元模型仿真分析得到LLSM定子与动子铁心各部分磁通密度波形,再进行频谱分析得到各次磁通密度分量;然后基于通用的铁耗分立计算模型计算了各次磁通密度分量对应的铁耗,再由铁耗叠加方法将三个区域磁通密度分量产生的损耗相加计算得到一段1.2 km长定子下LLSM的铁耗。对比了不同时速和不同材料时LLSM的铁耗,分析了运行速度以及铁心材料对铁耗的影响,为磁浮列车的性能分析提供借鉴。

2 LLSM铁耗计算模型

在不考虑谐波的理想情况下,LLSM长定子中铁耗是由励磁磁场与电枢磁场的合成行波磁场基波分量产生,而动子中铁耗则为零,因为动子与行波磁场同步。而实际上,由于铁心开槽引起的齿槽效应和励磁/电枢磁场的非正弦,铁心中存在比较大的谐波分量,导致铁心损耗增加,故铁耗计算时需要考虑谐波磁场。此时可以采用Giorgio Bertotti所提出的一种应用较为广泛的三项分立模型,因为其能够很好地考虑磁场各次谐波分量Bn产生的铁心损耗PIron[23]:

(1)

式中,Phy为磁滞损耗,由铁心中的交变磁通引起;Pcl为涡流损耗,由铁心中感生电势的涡流压降引起;Pex为附加损耗,由铁磁材料的巴克豪森效应产生,所占铁耗比例很小,可忽略不计;kh、kc和ke为三项损耗分别对应的损耗系数,kh和ke可以通过对硅钢片在不同频率和磁通密度下损耗的实测数据进行拟合得到,kc与材料的质量密度、厚度以及电导率有关;n为磁场谐波次数;f为电源频率。式(1)中各物理量均为国际单位。

可见,在求得LLSM铁心磁通密度的基波与谐波分量后,基于上述模型就可以计算得到各次磁通密度分量对应的铁耗。LLSM中所采用的M800-50A硅钢材料在5个频率下的损耗系数kh、ke见表1,采用参数拟合后就可以得到不同频率下的损耗系数。

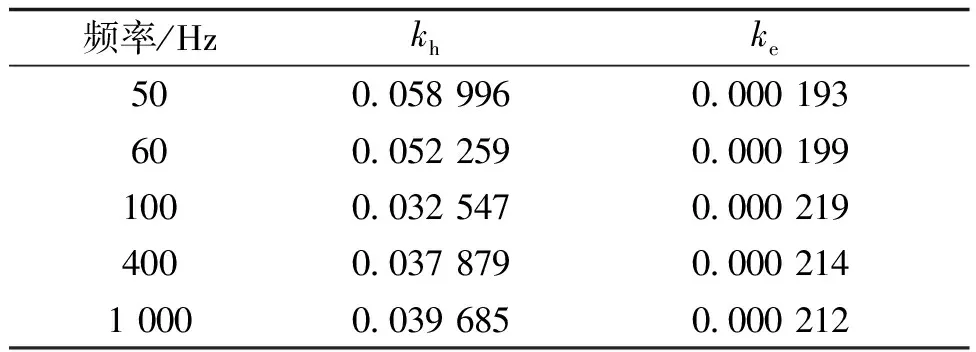
表1 M800-50A不同频率下损耗系数Tab.1 Loss coefficient of M800-50A

由式(1)可以看出,电机铁耗的大小主要由磁通密度各次分量幅值Bn和频率f决定,这两者可以从铁心磁通密度波形中获得,同时,也需要考虑磁通密度分布不均匀的问题。因此,本文采用了瞬态有限元模型来计算磁通密度波形,为了简化计算,磁通密度分布不均匀是根据磁场分布特性,在有限元模型中选择典型位置来求取平均值的方法解决。即通过有限元模型可以得到定动子齿部与轭部磁通密度各次分量的平均幅值,这也是目前铁耗分析中有效的计算手段。

3 LLSM结构与有限元模型

图1为TR08型高速磁浮列车下长定子直线同步电机结构和有限元计算模型示意图,列车轨道两侧为长定子段,每段铁心均匀分布开口槽,三相电枢绕组为单匝集中整距的波绕组结构,采用分段供电技术,每段LLSM定子长度通常为1.2 km。动子(悬浮磁极)采用电励磁的模块化结构,安装在列车下方,其长度由车辆编组数决定。端车一侧有7.5个悬浮模块,中车一侧有8个悬浮模块,以5编组为例,LLSM动子一侧长度为39个悬浮模块。

图1 LLSM结构和2D有限元模型Fig.1 Structure and 2D finite element model of LLSM

动子长度比长定子段要短,铁耗主要分布在动子覆盖区域的LLSM铁心中,而未被动子覆盖区域的定子铁耗很小,因为该区域的磁通密度很小,将这两部分分开计算。而对于被动子覆盖的区域,LLSM两端会受到端部效应的影响,中间部分则可以认为是分布相同的,因此需要通过两种模型来分析之间的差异。三种模型结构如图1所示,主要结构参数见表2。

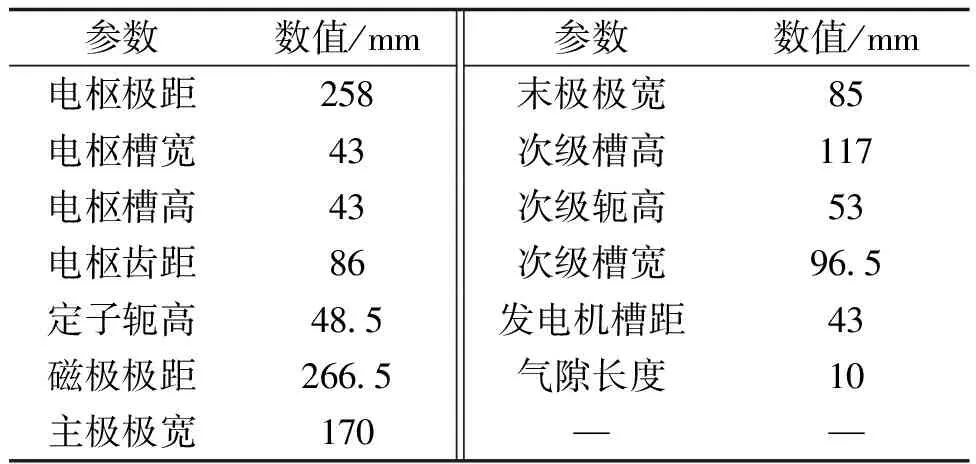
表2 LLSM主要结构参数Tab.2 Main structural parameters of LLSM

图1(b)为未被动子覆盖的长定子段;图1(c)为被动子覆盖的两个边端,其等效于两端的两个半悬浮电磁铁模块,长定子比动子要长,以实现瞬态运行仿真;图1(d)为被动子覆盖的中间部分,模型两端设置为对称边界条件。

以一个悬浮电磁铁模块进行建模分析,其包含10个中间主磁极和2个端部末磁极,主磁极极面宽于末磁极,且在磁极齿面上均匀开槽,嵌入绕组构成直线发电机。定动子铁心由M800-50A硅钢片叠压而成,图2为其磁化曲线和损耗曲线。

图2 M800-50A电磁性能曲线Fig.2 Electromagnetic performance curve of M800-50A

LLSM三种模型中定动子铁心表征齿部与轭部磁通密度的几个典型位置标注如图3所示。

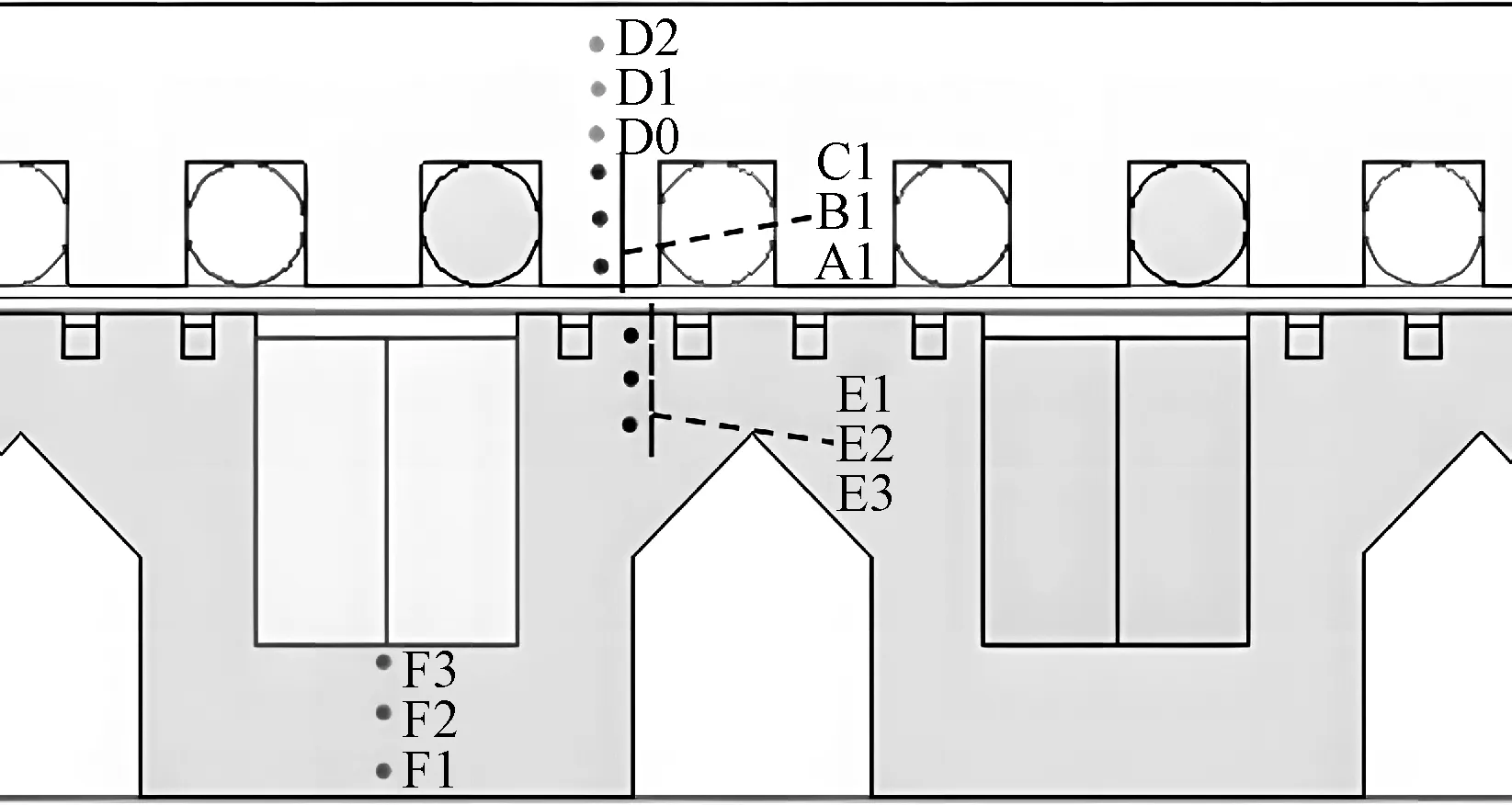
图3 LLSM齿部与轭部磁通密度的典型位置Fig.3 Typical positions of tooth and yoke magnetic flux density in LLSM

(1)定子铁心:考虑到定子开槽和漏磁的影响,故在定子齿部和轭部分别取3个位置A1、B1、C1和D0、D1、D2。

(2)动子铁心:受磁极形状与定子齿槽效应的影响,动子齿部磁通密度将会有较多的谐波分量,故在齿部部分取3个典型位置E1、E2、E3;对于轭部部分,其受谐波磁场的影响较小,磁通密度变化不大,选取3个典型位置F1、F2、F3。

基于以上三个瞬态LLSM有限元模型(电枢电流激励1 200 A,励磁电流激励20 A),在列车速度600 km/h下,仿真运行一个电周期就可以计算得到这些位置的磁通密度波形,其包括径向磁通密度BR(垂直分量)和切向磁通密度BT(水平分量)。经过频谱分析,就可以得到对应的磁通密度分量幅值BRn和BTn,从而得到式(1)中磁通密度幅值Bn为:

(2)

4 铁心磁通密度

4.1 未被动子覆盖的定子铁心磁通密度

图4为定子齿部与轭部3个位置的磁通密度波形(为了区分用W1/W2/W3和Y1/Y2/Y3来表示)。可以看出,未被动子覆盖的定子段铁心齿部和轭部的磁通密度幅值都很小,且主要为基波分量,故其铁耗占比很小。

4.2 动子覆盖端部区域定子铁心磁通密度

图5为动子覆盖端部区域定子铁心齿部和轭部的磁通密度垂直分量BR和水平分量BT的波形。从磁通密度波形中可以明显发现,齿部和轭部3个位置的磁通密度存在一些差异,分布不均匀。对于齿部,主要是因为漏磁的影响,同时齿部磁通密度以垂直分量BR为主。

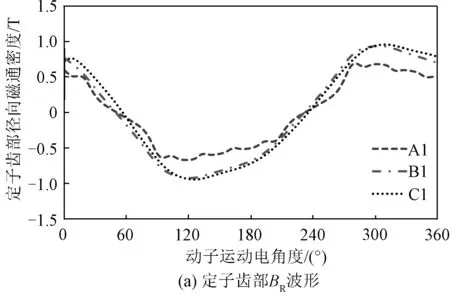
图5 动子覆盖端部LLSM定子铁心磁通密度及频谱分析Fig.5 Magnetic flux density of LLSM stator core in end area covered with mover and its frequency spectrum

通过对齿部和轭部各点的BR和BT进行频谱分析,分别求取各次磁通密度分量的垂直分量与水平分量,按式(2)求得各点的磁通密度幅值,再平均后就可以得到齿部和轭部的磁通密度,如图5(e)、图5(f)所示。可见,除基波分量外,定子齿部磁通密度还存在较多的谐波分量,其中3次、5次和7次等奇数次谐波影响较为显著,基波磁通密度幅值为0.906 T,3次谐波为0.091 T,5次谐波为0.062 T,7次谐波为0.027 T。LLSM的磁极形状如图3所示,其为凸极结构,一对极下对应6个定子槽,极弧系数为0.638,磁极形状导致气隙磁阻不均匀,在电机铁心未达到饱和时,气隙磁场中的3次谐波很大,同时,电机长定子部分为齿槽结构,存在明显的齿槽效应,会导致气隙磁场中存在5次、7次谐波,与文献[24]研究相关直线电机齿槽效应影响的结论一致。

分析图5中磁通密度波形可知,与定子齿部磁通密度相比,定子轭部磁通密度的谐波分量相对较小,即开槽所带来的齿谐波影响主要是影响定子齿部磁通密度。但是,通过频谱分析,如图5(f)所示,其同样也存在一些奇数次谐波,其中基波磁通密度幅值为0.829 T,3次谐波为0.046 T,5次谐波为0.011 T。同时可知,由于本模型考虑了纵向端部,其会导致端部磁场发生变化,产生空间上静止的磁场分量[25],即在定子齿部和轭部的磁通密度分量中均含有一定的直流分量,其在定子铁心中不产生铁心损耗;但是由于动子以同步速运行,则在动子铁心中产生的磁场为基波分量,所以会在端部区域的动子铁心中产生相应的铁心损耗。对于实际长定子下的LLSM,磁极连续布置,所以非端部的磁极不受纵向边端的影响,即由于边端效应引起的直流磁场,将导致端部区域动子铁心的铁耗要大于非端部区域。

4.3 动子覆盖中间区域定子铁心磁通密度

图6为动子覆盖中间区域定子铁心齿部和轭部3个位置的磁通密度波形。可见,中间定子铁心齿部与轭部的磁通密度变化趋势与端部定子铁心大体相同。通过频谱分析,如图6(e)和图6(f)所示,得到定子齿部基波磁通密度幅值为0.956 T,定子轭部基波磁通密度幅值为1.118 T,两者均比端部定子铁心的磁通密度分量大,故中间定子铁心损耗要比端部定子的大一些。

4.4 动子端部铁心磁通密度

图7为动子端部铁心齿部和轭部3个不同位置的磁通密度波形。由于动子运动,故在仿真求解模型中,所研究选择的位置是随动子一起运动的,这与定子部分所选择的固定位置不同。可见,动子铁心齿部的磁通密度波形呈现6次波动,这与前面分析受齿槽效应影响的结果一致。

图7 LLSM动子端部铁心磁通密度及频谱分析Fig.7 Magnetic flux density of LLSM mover end core and its frequency spectrum

从图7(e)和图7(f)的磁通密度频谱分析中可知,动子端部铁心齿部磁通密度除了直流分量,主要是6次谐波分量,其幅值为0.186 T,另外还有由前述所分析的端部定子磁场直流分量引起的基波分量。与动子齿部磁通密度相比,动子轭部磁通密度波形接近直流,谐波分量很小,即齿槽效应的影响主要集中于齿部,这一点与定子部分是相同的。频谱分析也表明,动子轭部磁通密度的6次谐波分量小于齿部,故其对铁耗的影响变小,另外,跟动子铁心齿部相同,其存在与6次谐波大小相近的基波分量。

4.5 动子中间铁心磁通密度

图8为选择的动子中间铁心齿部和轭部3个不同位置的磁通密度波形,其频谱分析如图8(e)和图8(f)所示。可见,与动子端部铁心磁通密度相比,两者的变化趋势相同,并且6次谐波磁通密度幅值相近。不同的是,动子中间铁心齿部和轭部磁通密度中不包含基波分量,故其损耗会小于端部动子的损耗。

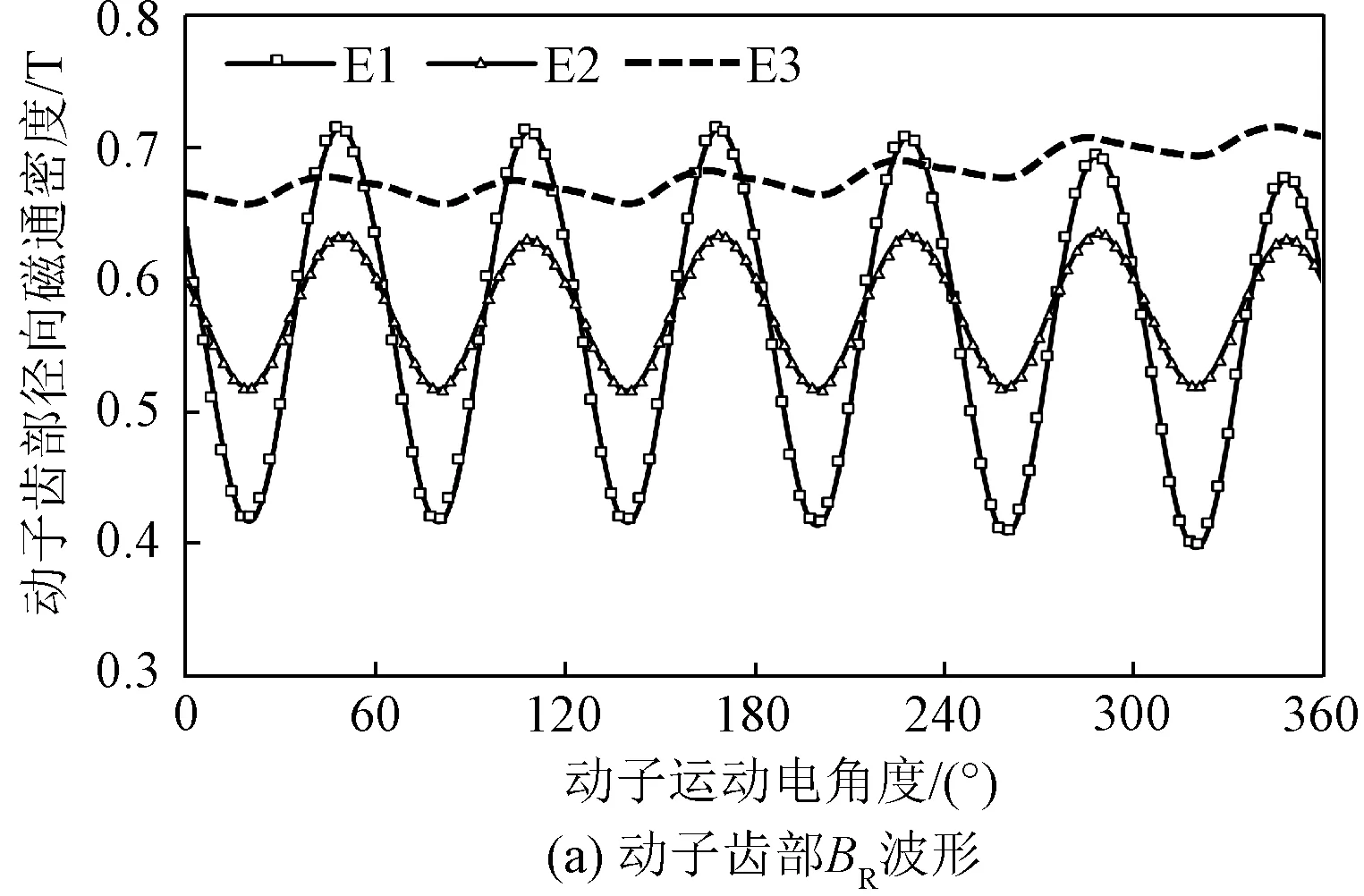
图8 LLSM动子中间铁心磁通密度及频谱分析Fig.8 Magnetic flux density of LLSM mover middle core and its frequency spectrum

从定动子铁心不同位置的磁通密度变化波形及频谱分析中可以看出,无论是定子铁心还是动子铁心,其磁通密度均含有谐波分量,其中定子铁心磁通密度以基波和奇数次谐波为主,动子铁心磁通密度则以6次及6倍次谐波为主。根据求得的LLSM铁心各部分磁通密度分量,基于铁耗计算模型,就可以得到各次磁通密度的谐波铁耗,再考虑未被动子覆盖的定子段、动子覆盖下的端部和中间的不同,叠加后就可准确计算出一段长定子下LLSM的铁耗。

5 铁耗分析

5.1 定子铁耗计算

考虑7次及以下的谐波,将动子覆盖端部和中间区域LLSM的定子铁心齿部和轭部磁通密度各次谐波分量分别代入式(1),就可以得到LLSM两个区域的定子齿部和轭部单位铁耗,见表3。

由表3可知,对于定子单位铁耗来说,在动子覆盖区域的定子铁心,齿部和轭部铁耗主要都由基波磁通密度产生,但端部区域与中间区域高次磁通密度谐波对应的铁耗所占分量不同。在端部定子铁心齿部铁耗中占15.8%,在轭部铁耗中占3.7%;在中间定子铁心齿部铁耗中占15.1%,在轭部铁耗中占2.3%。可见,高次磁通密度谐波产生的损耗主要在定子齿部。

对于未被动子覆盖的定子铁心,用上述同样的方法进行铁耗计算,可得其齿部单位铁耗为0.15 W/kg,轭部单位铁耗为0.1 W/kg,与动子覆盖下的定子铁心的单位铁耗相比要小很多,故其占整体铁耗比例很小。

根据LLSM的定子结构参数和所使用的铁心材料规格可计算得一个悬浮电磁铁模块下定子一段铁心的总质量为97.98 kg,其中定子齿部29.99 kg,定子轭部67.99 kg,故可得动子覆盖端部区域定子一段的铁耗为2.72 kW,有限元仿真结果为2.84 kW;动子覆盖中间区域定子一段的铁耗为4.16 kW,有限元仿真结果为4.26 kW。计算误差一方面是忽略了磁场中更高次谐波,另一方面是采用了3个位置所得到的平均磁通密度,是个近似值。

5.2 动子铁耗计算

与定子铁耗的计算方法相同,LLSM动子铁耗计算亦是将动子的齿部和轭部分开,将齿部与轭部磁通密度频谱分析后求得的各次谐波磁通密度均值,代入式(1)计算得到动子端部和中间齿部与轭部的单位铁耗见表4。

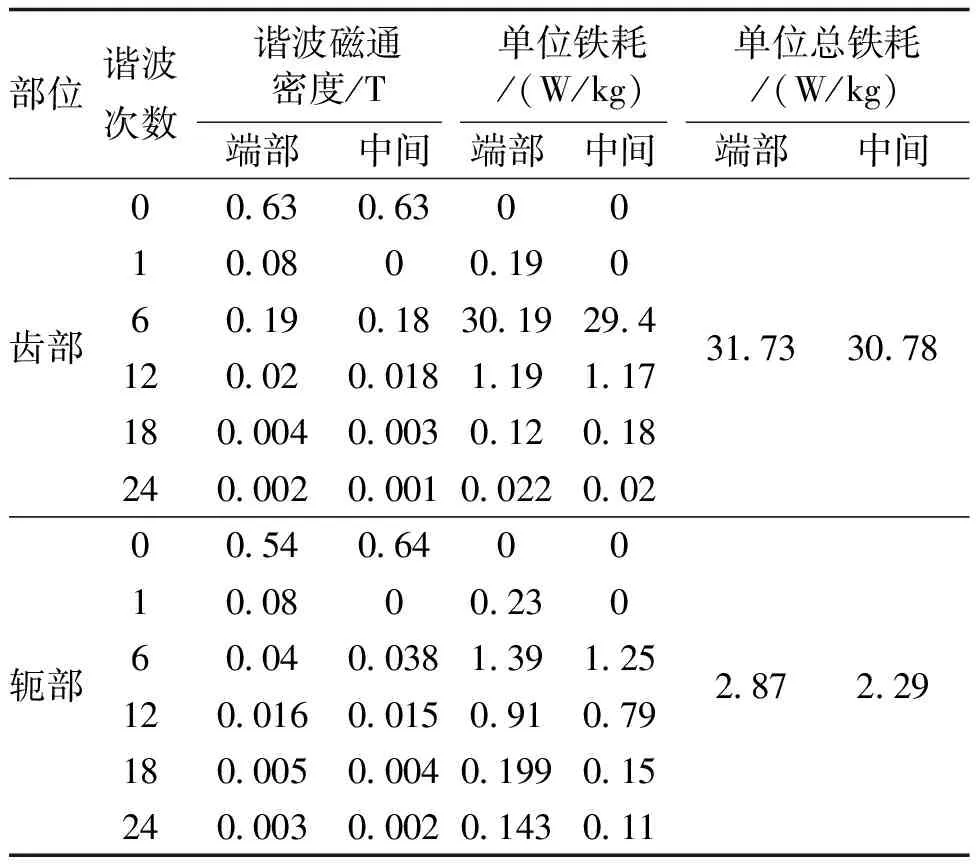
表4 LLSM动子单位铁耗Tab.4 Unit iron loss of LLSM mover

从表4中可以看出,动子铁耗主要由6次谐波磁通密度产生,齿部铁耗比轭部铁耗大,即铁耗主要集中在齿部,并且由于端部动子铁心受到定子侧直流磁场的影响,其铁耗比中间动子的要大。根据LLSM动子结构参数和铁心材料计算得一个悬浮电磁铁模块下动子部分的总质量为375.23 kg,其中动子齿部225.37 kg,动子轭部149.86 kg,依据表4中各部分单位铁耗,可计算得端部动子铁耗为7.59 kW,有限元仿真结果为7.84 kW;中间动子铁耗为7.28 kW,有限元仿真结果为7.44 kW。

结合定子部分的铁耗计算,可计算出一段1.2 km长定子下的LLSM定子总铁耗为469.485 kW,动子总铁耗为285.125 kW,动子铁耗值是定子铁耗的60.7%。

6 LLSM铁耗的影响因素

6.1 运行速度

假设LLSM的电流(电枢电流与励磁电流)保持不变,随着车辆运行速度增加,LLSM的电枢电流频率也随之增加。由式(1)可以看出,如果磁通密度保持不变,在电源频率随速度同步增加时,铁耗也随之增大。表5为利用上述同样计算方法得到的磁浮列车在不同运行速度下一段1.2 km长定子下LLSM的铁耗。显然,在1 000 km/h时,其铁耗值是600 km/h时的2.14倍。

表5 列车不同速度时LLSM铁耗Tab.5 Iron loss of LLSM at different speeds of train

在磁浮列车悬浮高度稳定时,此时可认为励磁电流保持不变,而电枢电流跟随列车运行状态、运行速度(加速、减速或匀速)发生变化。在不同速度下,计算得到列车的风阻、导轨磁阻力与直线发电机阻力等运行阻力,并假设加速度一定(0.8 m/s2),就可以得到LLSM所产生的电磁推力、相应的电枢电流与铜耗。一段1.2 km长定子下的LLSM铜耗与铁耗的对比如图9所示。可以看出,随着运行速度的提高,LLSM的铁耗和铜耗都在不断增大,且速度愈高,增加幅度愈大。由于列车速度与电源频率成正比,故电机定子的电枢电流频率也在同步增加,铁耗基本与电源频率的1.5次方成正比增大。

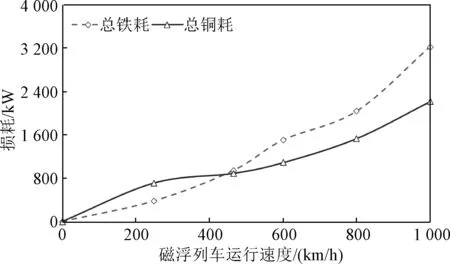
图9 列车不同速度下LLSM的铁耗和铜耗(加速度一定)Fig.9 Iron and copper loss of LLSM at different speeds of maglev train(fixed acceleration)

由图9可见,在中低速范围内,铜耗大于铁耗,而高于400 km/h后,铁耗就大于铜耗了。如果加速度增大,铜耗会随之增加,从而转折的速度点也会提高,理论上加速度大到一定值后,整个运行区域铜耗都会大于铁耗。实际运行时,高速时加速度比较小,低速时加速度比较大,即在高速时铁耗会比铜耗大。实际运行时,还存在线路馈电电缆的铜耗,这里的分析中没有包括在内。

磁浮列车匀速运行在600 km/h时,考虑未被动子覆盖的定子段铁耗,以及动子覆盖下端部和中间的铁耗差异,计算得一段1.2 km长定子下LLSM铜耗为1.09 MW、铁耗为1.52 MW,以现有高速磁浮列车系统配置为例,铁耗是总输出功率的0.064倍。

6.2 铁心材料

若要降低铁心损耗,LLSM铁心材料可以采用电机中常用的M470-50A。采用前述相同的分析方法,以图1(c)所示的动子覆盖下的端部模型为例,在保持相同的有限元仿真设置下得到定子齿部和轭部磁通密度波形,并与前面采用M800-50A所得到的波形进行了对比,如图10所示。可以看出,不同铁心材料下定子铁心齿部和轭部的磁通密度变化趋势相同,齿部磁通密度幅值非常接近,而轭部磁通密度略有不同,动子铁心磁通密度的对比与定子侧相似。同样,在列车运行速度为600 km/h时,利用上述相同计算方法可计算得到一段1.2 km长定子下LLSM铁耗值为1.34 MW,比使用前者M800-50A材料时损耗下降11.8%。因此,在其他条件相同的情况下,磁浮列车LLSM铁心材料采用M470-50A时,铁耗会降低,从而列车运行效率提高。

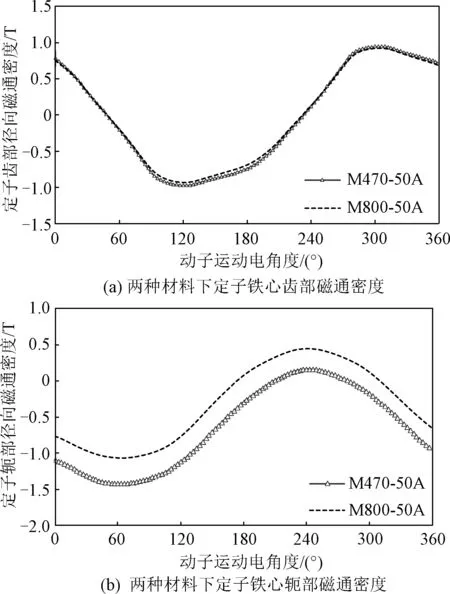
图10 两种材料下定子铁心齿部和轭部磁通密度Fig.10 Magnetic flux density of stator core teeth and yoke by adopting two different materials

以上LLSM铁耗结果是先基于有限元分析软件计算铁心磁场然后再计算得到的,如果要进行实验验证,必须要在实际线路或大型试验台高速运行状态下测试,目前国内不具备相应的测试条件和测试环境。虽然无法进行实验测量,但是基于有限元方法仿真计算是电机领域常用的有效手段,所建立的模型结构参数与实际应用相同,也得到了充分的验证,因此分析得到的磁场与铁耗都是可信的。

7 结论

基于LLSM的三种瞬态有限元模型,在不考虑电机变频器供电电流谐波的影响下,分析了LLSM不同位置的磁场分布,获得了铁心各部分磁通密度的基波和谐波分量。基于铁耗分立计算模型,计算了不同运行速度和不同铁心材料下LLSM的铁耗。得到的相关结论如下:

(1)由于定子齿槽效应,LLSM动子铁心中也存在铁耗,主要由6次及6倍次谐波磁通密度产生并主要分布在动子齿部,一段1.2 km长定子下的LLSM动子铁耗是定子铁耗的60.7%。

(2)受端部效应的影响,LLSM动子端部铁心磁通密度中存在基波分量,导致其损耗比动子中间铁心的要大。

(3)随着磁浮列车运行速度的提升,LLSM铁耗不断增大。当匀速运行于600 km/h时,铁心采用M800-50A时铁耗是总输出功率的0.064倍,而采用M470-50A时则可下降为0.055,列车的运行效率会提高。

本文研究内容及结论对高速磁浮列车的设计与控制提供了参考,下一步将研究考虑LLSM变流器供电下定动子的铁耗。