流线型长度对重联高速列车明线运行气动性能的影响
谢子豪,武振锋,李健,安乐
(1.中南大学 交通运输工程学院 轨道交通安全教育部重点实验室,湖南 长沙,410075;2.中南大学 轨道交通安全关键技术国际合作联合实验室,湖南 长沙,410075;3.中南大学 轨道交通列车安全保障技术国家地方联合工程研究中心,湖南 长沙,410075;4.兰州交通大学 机电工程学院,甘肃 兰州,730070)
影响列车气动性能的因素主要有列车自身结构形状、天气环境和道路结构等[1-4]。随着运行速度不断提高,列车运行的平稳性和安全性所面临的挑战也越来越严峻。通过数值模拟、缩比模型试验以及实车试验等方式探究不同形状的列车在不同环境下运行时的气动特性,分析和归纳各种变量对列车气动性能的影响,这一直是列车空气动力学领域的研究热点[5-8]。杜健等[9]将鲨鱼表皮非光滑沟槽结构运用于列车表面,仿真结果表明采用仿生结构的新型高速列车减阻率可达6%以上。NIU 等[10]将数值模拟方法和全尺寸试验相结合,优化了风挡的结构形式,有效提升了列车气动性能。于梦阁等[11]将多目标遗传算法与传统计算流体力学方法相结合,依据算法不断地修改列车参数化模型,进行自动寻优设计,以提高列车在侧风作用下的气动性能。KU 等[12]通过优化算法,改进了列车头部的几何外形,降低了列车进入隧道产生的微气压波强度。CHEN等[13]分析了车鼻长度对横风下列车空气动力性能的影响,发现鼻尖长度显著影响头车迎风侧和尾车背风侧的压力系数。为了进一步保障大风地区的行车安全,杨伟超等[14]设计了2 种挡风墙端部的气动缓冲结构。LI 等[15]通过增大隧道两端截面面积和减小隧道中部截面面积的方式,缓解列车进入隧道时的气动效应,并通过动模型试验验证了数值模拟计算结果的准确性。
与普通客运列车相比,高速列车虽然速度有很大提升,但是多为8 辆或16 辆固定编组,在编组方式上缺乏灵活性。为了提高运输效率,将2列8辆编组的高速列车连挂在一起,组成16辆编组的重联高速列车来提高运输能力已经成为一种常态化现象。虽然重联高速列车在高速铁路运输系统中扮演越来越重要的角色,但以重联列车为研究对象的列车空气动力学研究未广泛展开[16]。LI等[17]研究了重联区域车鼻间隙对重联列车气动性能的影响,发现重联列的阻力随着车鼻间隙增大而增大。NIU等[18]通过数值模拟的方法,研究了重联列车在多种环境下运行时的气动特性。梁习锋等[19]使用改进的延迟分离涡模拟(IDDES)方法,研究了横风环境下转向架和风挡的平滑程度对重联高速列车气动性能的影响。但两者所使用的计算模型均为4辆编组的重联高速列车,并未包含中间车。黄志祥等[20]通过风洞试验发现,8辆编组的高速列车在数值模拟计算时可以简化为“头车+中间车+尾车”这种3 辆编组形式,也指出了忽略中间车的2 车编组计算模型会增大尾车气动力偏差。GUO 等[21]研究了重联列车在横风环境下运行时的气动特性,并指出重联区域的存在会增大列车气动阻力。李爽等[22]使用滑移网格方法,模拟了重联列车进出隧道的动态过程,发现重联区域进入隧道时产生的压缩波和膨胀波时间间隔较短,导致膨胀效应和压缩效应相互抵消,进而使得列车表面压力以及隧道壁面压力无明显变化。上述2项研究内容均以某一运行条件下重联列车与非重联列车的气动性能差异为重点,当运行条件改变时,2种列车的气动性能的变化有待进一步探究。
综上所述,国内外对于非重联列车的气动性能优化的研究主要集中于优化列车自身形状以及挡风墙、隧道截面等外界线路条件这些方面。对于重联列车而言,现阶段研究内容仍集中于对比其与非重联列车在相同环境下运行时的气动性能差异。列车头型、头车流线型长度、横风速度、隧道长度、隧道断面形状等因素对重联列车气动性能的影响尚不明晰。为此,本文以流线型长度为切入点,选取列车在明线匀速运行这一代表性工况进行研究。
1 几何模型
在实际运营时,重联高速列车通常由2列8辆编组的高速列车连挂组成。为了保证计算精度并提高计算效率,列车计算模型均会有所简化。郗艳红[23]研究表明,当气流流过头车顶部一定距离后,列车壁面扰流边界层结构和各项气动力变化已经趋于稳定。因此,将8辆编组的计算模型缩短为3辆编组的计算模型,这不会改变列车流场结构的基本特征。本文将采用的列车模型简化为6辆编组。流线型长度为12 m 的列车计算模型如图1所示。由图1 可知:非重联列车由1 节头车、1 节尾车以及4 节中间车组成;重联列车由2 节头车、2节尾车以及2 节中间车组成。2 种形式的列车头车长度均为27 m,中间车长度均为25 m。重联列车总长度为158 m,非重联列车总长度为154 m。除了通过缩短列车长度来简化计算模型外,本文还对所采用的计算模型表面进行了光滑处理,各节车辆之间采用全封闭式风挡平滑过度,删除受电弓、雨刮器等车体外表面装置。由于计算模型数量较多(共计6 组),相同类型的计算模型除头尾车流线长度有所不同,头车长度、列车总长度以及其余位置的结构样式和形状尺寸完全一致,故图1仅展示2列完整计算模型。
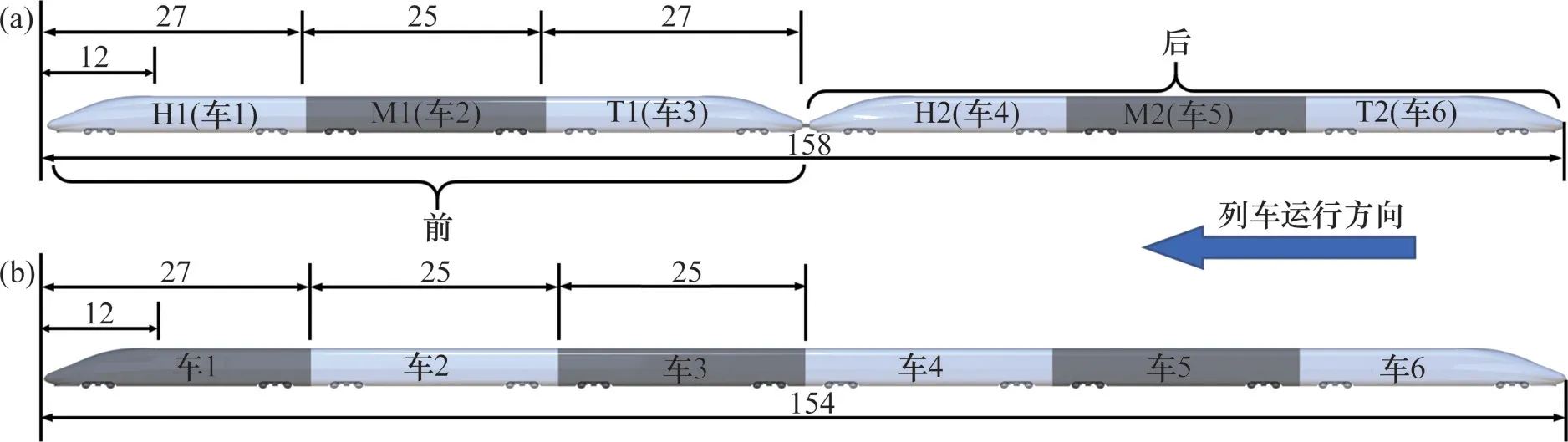
图1 整车计算模型Fig.1 Calculation model of whole train
此外,为了方便后续表述与对比,按照列车前进方向对各节车辆进行了单独命名。图1中6辆编组高速列车的各节车辆分别以车1、车2、…、车6进行命名。重联列车车体结构具有对称性,为便于单独分析讨论,故再次对其各节车辆进行单独命名。如图1(a)所示,H1,M1,T1分别代表前半部分列车的头车、中间车、尾车;H2,M2,T2则分别代表后半部分列车的头车、中间车、尾车。图2展示了3种不同流线型长度的头车模型,是对计算模型的补充。

图2 不同流线型长度的头车模型Fig.2 Head car with different streamlined lengths
2 数值模拟
2.1 计算域、网格及边界条件
在实际运行时,列车周围的流场可以视为无限大。但数值模拟只能在有限区域内进行求解计算。由于列车是明线匀速运行,因此,可使列车静止,通过设定计算域入口来流速度来模拟列车的实际运行状态。根据《铁路应用空气动力学第4部分:列车空气动力学性能与数值仿真规范》的相关要求,计算域须以列车高度h(h=4.0 m)为特征尺寸。列车明线匀速运行时的计算域及边界条件如图3所示。由图3 可知:计算域的高度为10h,宽度为20h,计算域的上游边界(面ABCD)距离列车头部鼻端为10h,计算域下游边界(面GHEF)距离列车尾部鼻端为40h。计算区域的上游边界(面ABCD)设为速度入口,计算域下游边界(面GHEF)设为压力出口,计算区域底部边界(面BCFH)设为无滑移运动壁面,速度与列车运行速度相同方向相反。其余边界(面ABHG、面ADEG、面DCFE)均设为对称边界条件。
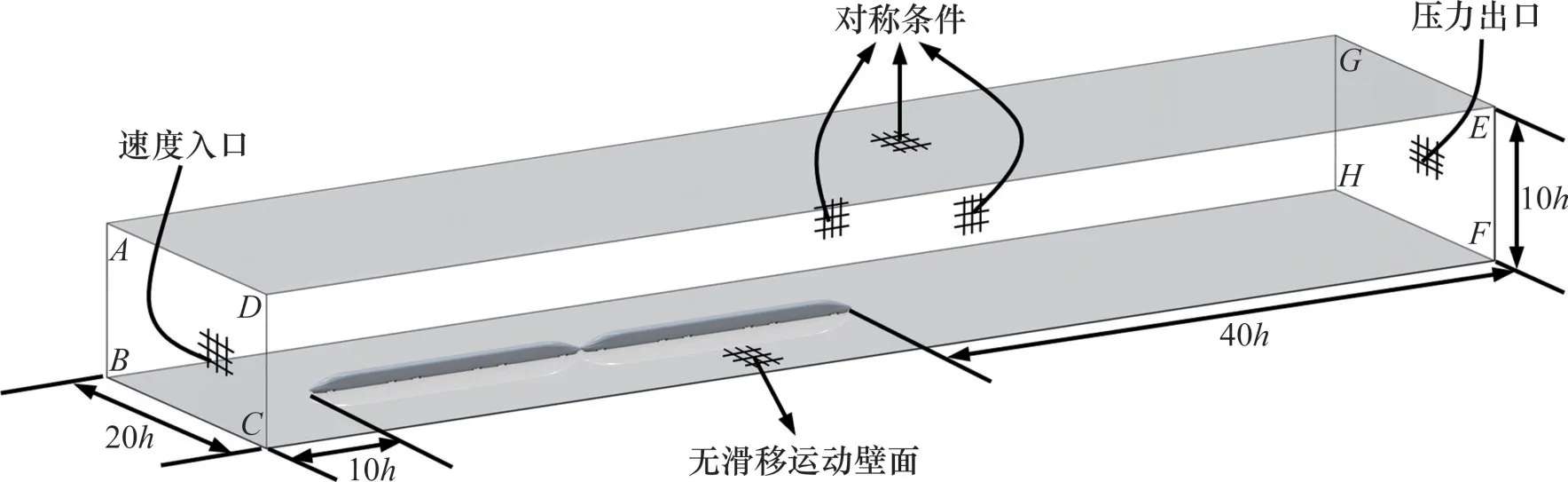
图3 计算域及边界条件Fig.3 Calculation domain and boundary conditions
网格划分是CFD 计算的重要前处理环节,网格质量以及网格数量会直接影响计算结果。为了保证计算精度,同时避免过多的网格数量影响计算效率,在进行计算域网格划分时,对车体近表面区域的网格进行加密处理,对远离车体表面区域的网格,应适当扩大网格尺寸以降低网格数量。对于排障器、裙板以及其他车体表面曲率变化较大的区域则需要减小网格尺寸,确保最大程度地还原列车表面特征形状。此外,为确保近壁面区域流动的模拟准确性,列车表面需划分边界层网格。本文在计算模型表面设置10 层边界层网格,第1 层网格厚度为0.2 mm,增长率为1.2,车体表面y+分布在40~200 之间。列车表面网格以及计算域体网格如图4所示。

图4 头车面网格及计算域体网格Fig.4 Surface mesh of head car and volume grid of calculation domain
2.2 网格独立性验证
为排除网格数量对计算结果准确度的影响,将流线型长度为12 m 的重联高速列车模型作为验证模型,划分A、B、C共3套网格,网格数量分别为1 300万、2 500万和3 800万。对比列车以300 km/h的速度匀速运行时头车、尾车的阻力和升力,判断网格数量是否满足计算精度要求。网格无关性验证计算结果见表1。由表1可知:B、C两套网格的计算结果最大相对误差仅为1.22%,继续增加网格数量对计算结果影响甚微。因此,综合考虑计算精度和计算成本,网格数量控制在2 500万左右较合适。

表1 网格无关性验证计算结果Table 1 Calculation results of mesh independence
2.3 数值计算方法可靠性验证
由于列车在明线匀速运行,且最大速度不超过350 km/h,故采用三维、定常、不可压缩N-S方程和标准k-ε两方程湍流模型进行模拟计算。为了确保计算结果的准确性,需对计算方法进行可靠性验证。张在中等[24]在中国空气动力研究与发展中心的风洞第2试验段完成了CRH2型高速列车的相关气动参数测试。试验模型比例为1∶8,列车模型为3辆编组形式,即头车+中间车+尾车,车辆之间采用半封闭外风挡连接,且安装了转向架。本文根据文献[24],将计算区域的来流速度分别设为30、60和90 m/s、并按照上述方法对CRH2型高速列车进行气动性能模拟计算。CHR2型高速列车计算模型如图5所示。

图5 CRH2高速列车计算模型Fig.5 Calculation model of CRH2 high-speed train
为方便将模拟数据与风洞试验数据进行对比,将阻力系数Cd及升力系数Cl定义如下:
式中:ρ为空气密度,取1.225 kg/m3;v为来流速度,m/s;S为与列车形状尺寸相关的参考面积,CRH2型高速列车的迎风面积为11.2 m2,试验模型比例为1∶8,故此处取0.175 m2;Fd为气动阻力;Fl为升力。
通过数值模拟得到列车的气动阻力系数,计算结果与风洞试验结果对比情况见表2。由表2 可知:CRH2型列车计算模型头车、尾车的阻力系数模拟值与实验值的最大相对误差为-5.5%。CRH2型列车计算模型的升力系数模拟值与实验值的最大相对误差为8.0%。计算值与实验值存在误差主要有2个方面原因:
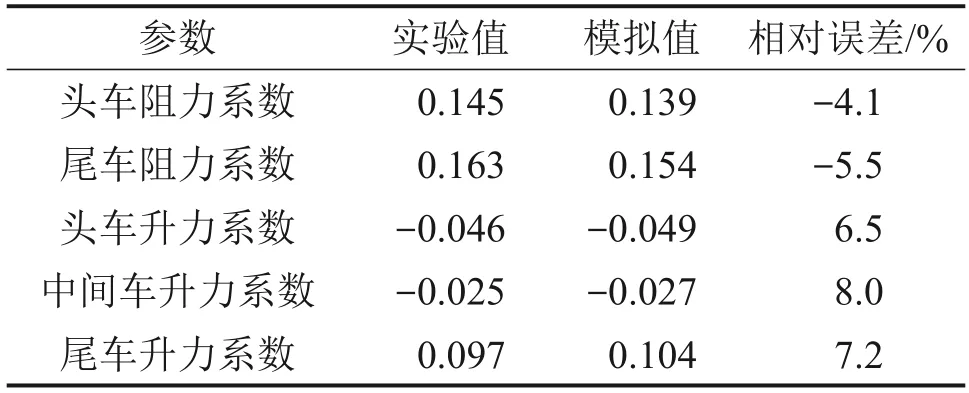
表2 CRH2型列车气动力系数实验值与模拟值对比Table 2 Comparison of experimental results and simulation results on aerodynamic coefficients of CRH2 train
1)风洞实验采用的等比模型与模拟计算采用的数字模型无法保证完全一致;
2)在数值模拟过程中,来流为均匀风,而风洞实验由于受洞壁、地面等因素的影响,不能完全保证均匀送风。
由以上分析可知,数值模拟计算结果与风洞实验结果之间的误差在合理范围内,即证明了本文所采用的数值模拟方法的合理性。
3 结果与分析
3.1 流线型长度对阻力的影响
在列车运行时,气动阻力是衡量列车气动性能的关键指标。在不同速度下,3种流线型长度的重联列车与非重联列车的总阻力如图6所示。

图6 不同速度下的列车气动总阻力Fig.6 Total aerodynamic drag of train under different running speeds
由图6 可知:无论是重联列车还是非重联列车,列车气动阻力均随着流线型长度增加而减小;在流线型长度从6 m 增加到12 m,重联列车在250、300以及350 km/h这3种速度下,阻力降低幅度均在16%左右;在相同速度等级下,非重联列车阻力降幅平均为12.6%。虽然重联列车阻力降低幅度要大于非重联列车,但是从图6可以看出,重联列车的总阻力要明显大于非重联列车的总阻力。由此可知,随着流线型长度增加,2种列车的阻力差距逐渐减小。
为了深入分析造成2种列车阻力产生差异的原因,需要关注各节车辆的阻力分布情况,各车辆气动阻力随速度变化曲线如图7所示。
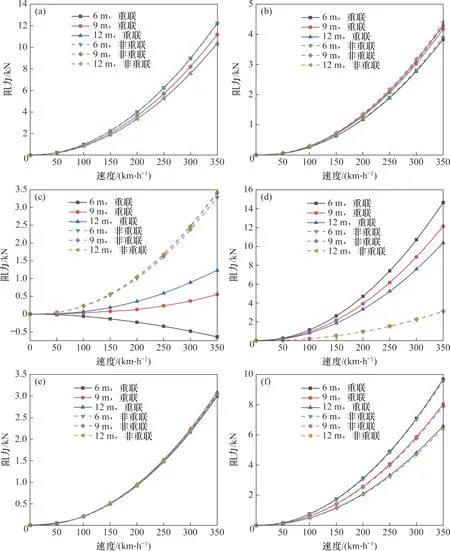
图7 各车辆在不同运行速度下的气动阻力Fig.7 Aerodynamic drag of each car under different running speeds
由图7(a)和图7(f)可知:流线型长度对头车和尾车的阻力有明显影响,且重联列车的头车阻力、尾车阻力分别与非重联列车头、尾车阻力基本一致,头车阻力和尾车阻力降低幅度分别为15%和30%。具体降低幅度见表3。

表3 头车及尾车阻力降低幅度(流线型长度为12 m)Table 3 Drag reduction of head car and tail car(streamlined length is 12 m)
由图7(c)和7(e)可知,不同颜色的虚线近乎完全重合,即对于非重联列车而言,流线型长度变化时,中间车气动阻力基本不变。而车2由于与头车相邻,故流线型长度变化会对其阻力产生一定程度的影响。由图7(b)可知,头车流线型长度越长,车2的阻力越大。
对于非重联列车而言,车3、车4 均为普通车辆。而重联列车在相同位置的车辆则是T1 和H2,分别对应前方列车的尾车以及后方列车的头车。与非重联列车的车3和车4之间的无缝平滑过渡不同,受列车头部流线型形状的影响,T1车辆和H2车辆构成的重联区域存在V形缺口,这是导致T1、H2两节车辆的阻力和车3、车4两节车辆的阻力有显著区别的主要原因。由图7(c)可知:非重联列车车3 的气动阻力要明显大于重联列车T1 的气动阻力;随着流线型长度增加,重联列车T1 车辆的阻力逐渐增大,并经历了由负到正的变化过程。这与通常情况下流线型长度增加、列车阻力减小的规律相反。由图7(d)可知:在速度相同时,非重联列车车4 的气动阻力明显小于重联列车H2 车辆的阻力,且H2车辆的阻力随着流线型长度增加而逐渐减小。
由于重联列车具有结构对称性,故将其分为前后2 列3 辆编组的列车,对阻力变化进行讨论。不同速度下重联列车前后两部分的气动阻力对比如图8所示。
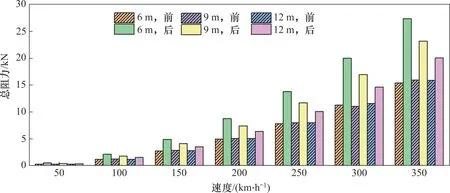
图8 不同速度下重联列车前后两部分的气动阻力Fig.8 Aerodynamic drag of head car and tail car of double unit high speed train under different running speeds
由图8可知:随着流线型长度增加,后方列车的阻力逐渐降低,而前方列车的阻力则无明显变化;当流线型长度为6 m 时,前方列车的阻力最小;当流线型长度为9 m 和12 m 时,前方列车阻力差距较小。由图7(c)可知:当流线型长度为6 m时,T1(车3)车辆的阻力为负值,故此时H1、M1、T1 这3 节车辆的阻力之和最小;随着流线型长度增加,T1 车辆的阻力增大,H1 车辆的阻力减小,二者相互抵消,导致前半部分列车的总阻力变化幅度较小。
不同位置处头车和尾车的阻力系数如图9所示(参考面积S为12.02 m2)。由图9(a)可知:车1和车4 分别作为前后2 列列车的头车,阻力系数均随着流线型长度增加而逐渐降低,但车4的降低幅度更大;当流线型长度从6 m增加到12 m,车4阻力系数降低了29.2%,车1 阻力系数仅降低15.2%;当流线型长度为12 m 时,两车阻力系数接近;当流线型长度为6 m 时,车4 的阻力系数比车1 高出16.2%。这说明随着流线型长度增加,两者的气动特性逐渐趋同。
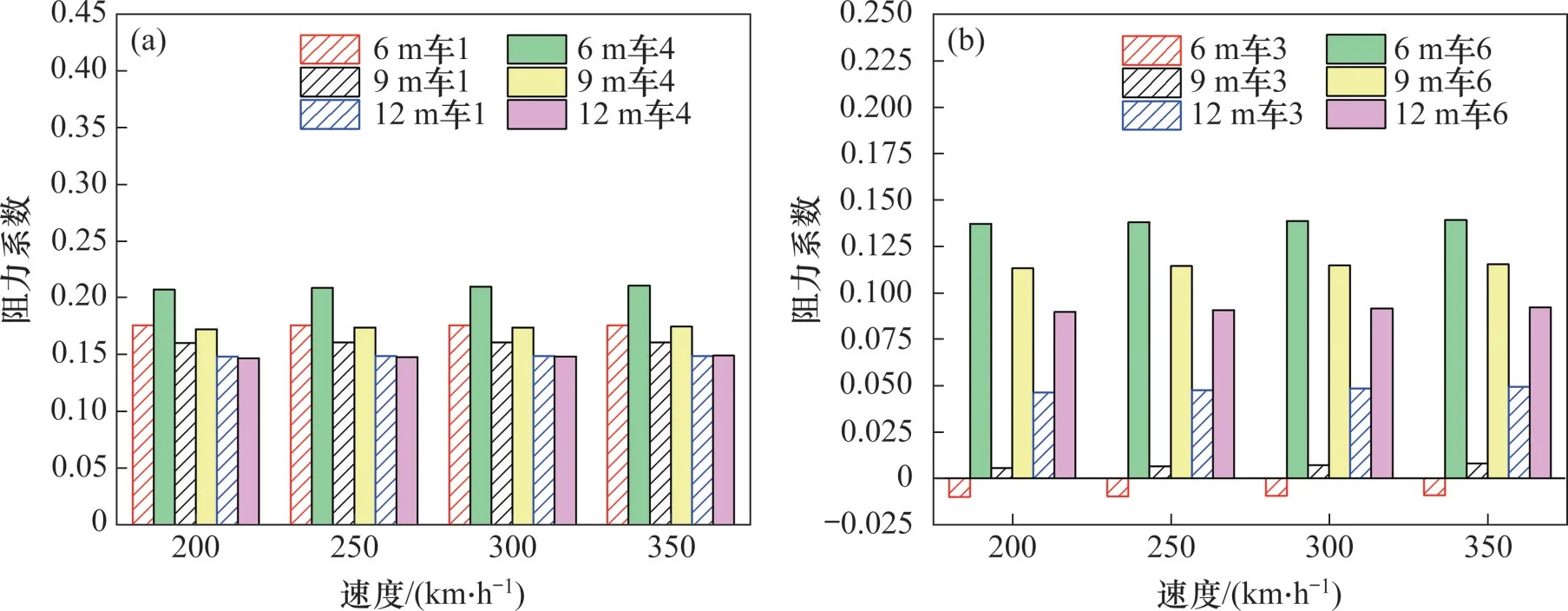
图9 重联列车头车及尾车阻力系数对比Fig.9 Comparison of drag coefficients of head car and tail car of double unit high speed train
由图9(b)可知:车3 和车6 的阻力系数无论是数值上还是变化趋势上均无任何相似性,但随着流线型长度增加,二者的阻力系数不断接近。虽然流线型长度为12 m 时,二者的阻力系数仍相差46.5%,但流线型长度6 m 时,两者阻力系数相差106.6%。可以发现随着流线型长度增加,阻力系数趋同的特点在尾车上也有所体现。
3.2 流线型长度对升力的影响
由于列车各节车辆的气动升力相对独立,没有气动阻力那样的求和关系,故需对各车辆气动升力单独讨论。各车辆在不同速度时的升力变化如图10所示。由图10可知:流线型长度变化对头车(车1)和尾车(车6)升力影响最直接;当运行速度为350 km/h 时,流线型长度从6 m 增加到12 m,重联列车头车升力降低了27.8%,尾车升力降低了43.7%;非重联列车头车、尾车升力的降低幅度与重联列车基本相同。重联列车和非重联列车相比,升力区别主要集中于车3(T1)和车4(H2)这2 节车辆。非重联列车车3 和车4 这2 节车辆均是形状相同的普通中间车,因而升力基本一致。由于这2节车辆处于整列车的中间位置,故流线型长度变化对这2 节车辆升力影响甚微。T1、H2 车辆分别为重联列车前半部分的尾车和后半部分的头车,受重联区域V形缺口的影响,2节车辆的升力要显著大于非重联列车车3和车4的升力。

图10 各车辆在不同运行速度下的升力Fig.10 Aerodynamic lift of each car under different running speeds
单独观察重联列车升力变化曲线发现:头车(H1、H2)升力均为负值,尾车(T1、T2)升力均为正值,但流线型长度变化对这4节车辆的升力的作用效果并不一致。H1头车和T2尾车位于整列车的前后两端,其升力和变化趋势与非重联列车的头车、尾车基本一致,即升力随着流线型长度增加而逐渐降低。如图10(c)和图10(d)所示,T1 和H2两节车辆的升力变化曲线迥然不同。T1 车辆作为重联列车前半部分列车的尾部,升力为正且绝对值随流线型长度增加而逐渐减小。H2 车辆作为后半部分列车的头车,升力为负且绝对值随流线型长度增加而增加。
3.3 流线型长度对表面压力的影响
3.1节和3.2节详细说明了流线型长度变化对列车气动阻力和升力的影响,但仍需分析列车表面压力分布以及流场内压力分布,以便解释气动力变化的原因。计算域纵剖面压力分布如图11所示。
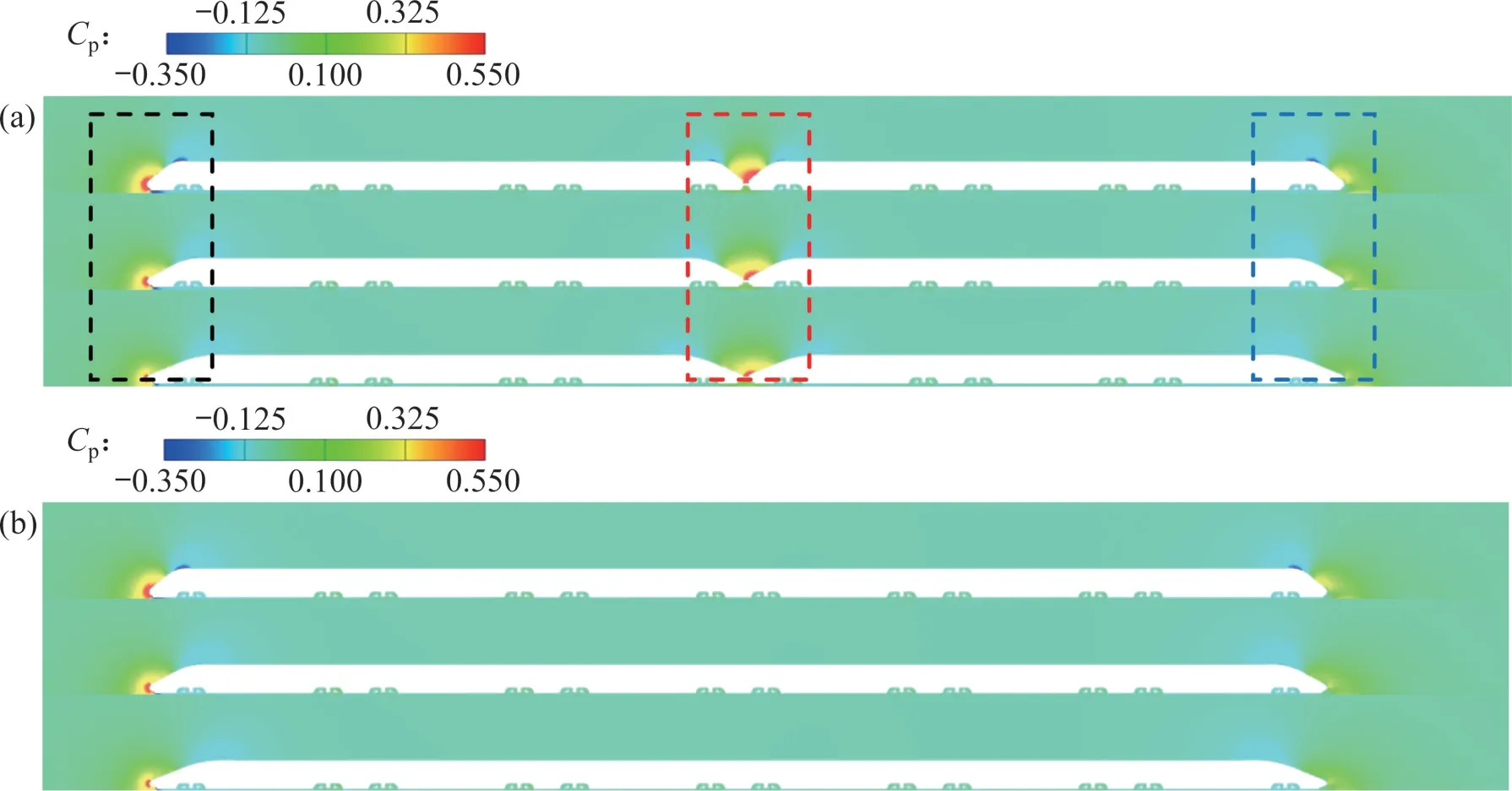
图11 计算域纵剖面压力分布Fig.11 Pressure distribution on longitudinal section of domain
从图11 可以发现:重联列车纵剖面压力分布与非重联列车纵剖面压力分布高度相似,仅在重联区域有明显差异。如图11(a)中黑色线框围成的区域所示,流线型长度变化会对列车鼻尖四周以及头车司机室顶部这2处区域的压力分布产生直接影响。流线型长度增加,列车鼻尖处的深红色高压区范围逐渐减小,司机室顶部的深蓝色低压区范围也逐渐减小并最终消失。图11(a)中的蓝色线框所围区域中的高压区范围和低压区范围也随着流线型长度增加而逐步减小。高压区范围减小直接使得头车前后的压力差减小,进而使得压差阻力降低。因此,流线型长度通过影响列车前后两端的压力差来影响阻力。
图11(a)中的红色线框所围的重联区域压力变化趋势也与上述情况相同,但对重联区域前后2节车辆的影响结果不同。当流线型长度为6 m时,重联区域的高压区范围最大。T1 车辆前后两端的压力差小于0 kPa,这是T1 车辆在流线型长度为6 m时,阻力为负值的根本原因。随着流线型长度逐渐增大,重联区域高压区范围逐渐缩小。此时,对于T1 车辆而言,车辆前后两端的压力差逐渐增大,阻力也随之增大。对于H2车辆而言,车辆前端的压力减小,导致车辆两端的压力差减小,故阻力也随之降低。此外,随着流线型长度增加,重连区域V 形缺口逐渐变大,尾车与头车之间的过渡更加平缓。车4的鼻尖压力逐渐降低,车鼻四周压力分布形式与车1对应位置的压力分布形式更接近。即流线型长度越长,后方头车的气动特性越接近前方头车气动特性。
图12所示为运行速度为300 km/h 时,不同流线型长度的重联列车头车及尾车的压力云图。由图12(a)~(c)可知:随着流线型长度增加,头车H1、H2以及尾车T1车体表面高压区范围显著降低;当流线型长度为6 m时,高压区首先集中分布在头车鼻尖和排障器前端这2处位置,其次分布在车鼻向司机室的过渡段以及司机室挡风玻璃的下端;当流线型长度为12 m时,不仅车鼻和排障器前端这2处位置的高压区影响范围明显缩小,而且司机室挡风玻璃下端以及上述过渡区已无明显高压分布。通过图12(b)和12(d)可以发现,尾车T1、T2 司机室四周的低压区影响范围也随着流线型长度增加而逐渐减小,即列车流线型长度越长,表面压力的绝对值越小。
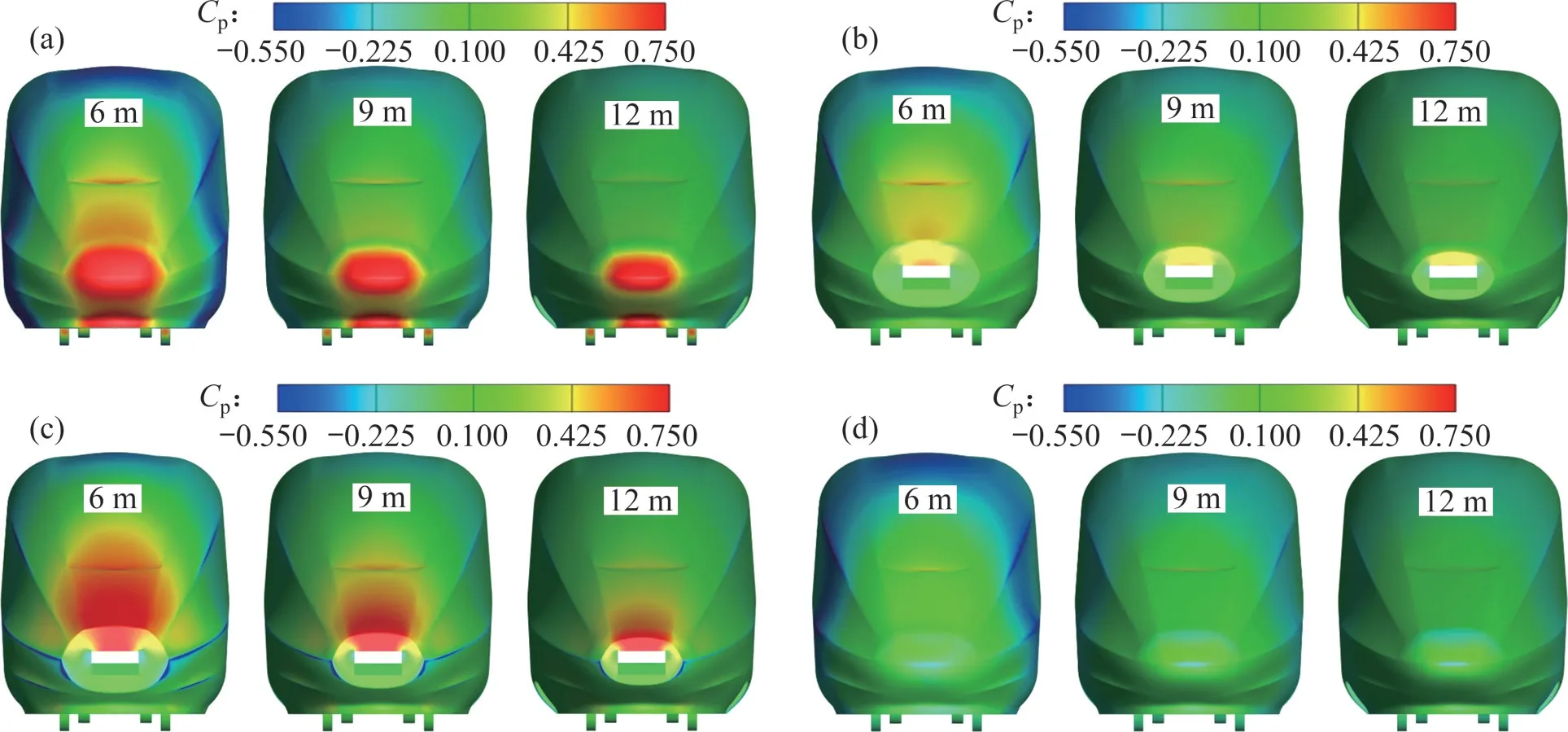
图12 速度为300 km/h时的头车和尾车表面压力分布Fig.12 Pressure distribution on surface of head car and tail car(300 km/h)
对比图12(a)和12(c)可以发现:高压区在头车H2表面的影响范围要明显大于其在头车H1表面的作用范围。由图12(b)和12(d)可知:T1 和T2 虽然均为尾车,但两者车体表面的压力分布截然不同;T1车体表面压力要明显高于T2车体表面压力,这一点在流线型长度为6 m时最明显。这一现象既解释了重联列车前半部分列车的阻力小于后半部分列车阻力的原因,即前半部分列车的压差阻力小于后半部分列车的压差阻力,同时再次证明了流线型长度变化会直接影响列车前后表面压力差,进而使阻力发生变化。
当列车运行速度为300 km/h 时,列车纵剖面压力变化曲线如图13所示。由图13可知,中间车车顶处的表面压力接近于0 kPa 且基本稳定不变,但是在头车车顶和尾车车顶的流线型区段内,车体表面压力会产生较大波动。重联列车相比于非重联列车多了1节头车和1节尾车,故在压力变化曲线在重联区段内会多发生1 次波动。从图13(a)可以看出,受重联列车结构对称性的影响,表面压力在后半部分列车的变化形式与前半部分列车基本一致,仅在数值上存在差异。从图13 的局部放大细节可知,流线型长度会对列车表面压力造成2个方面影响:
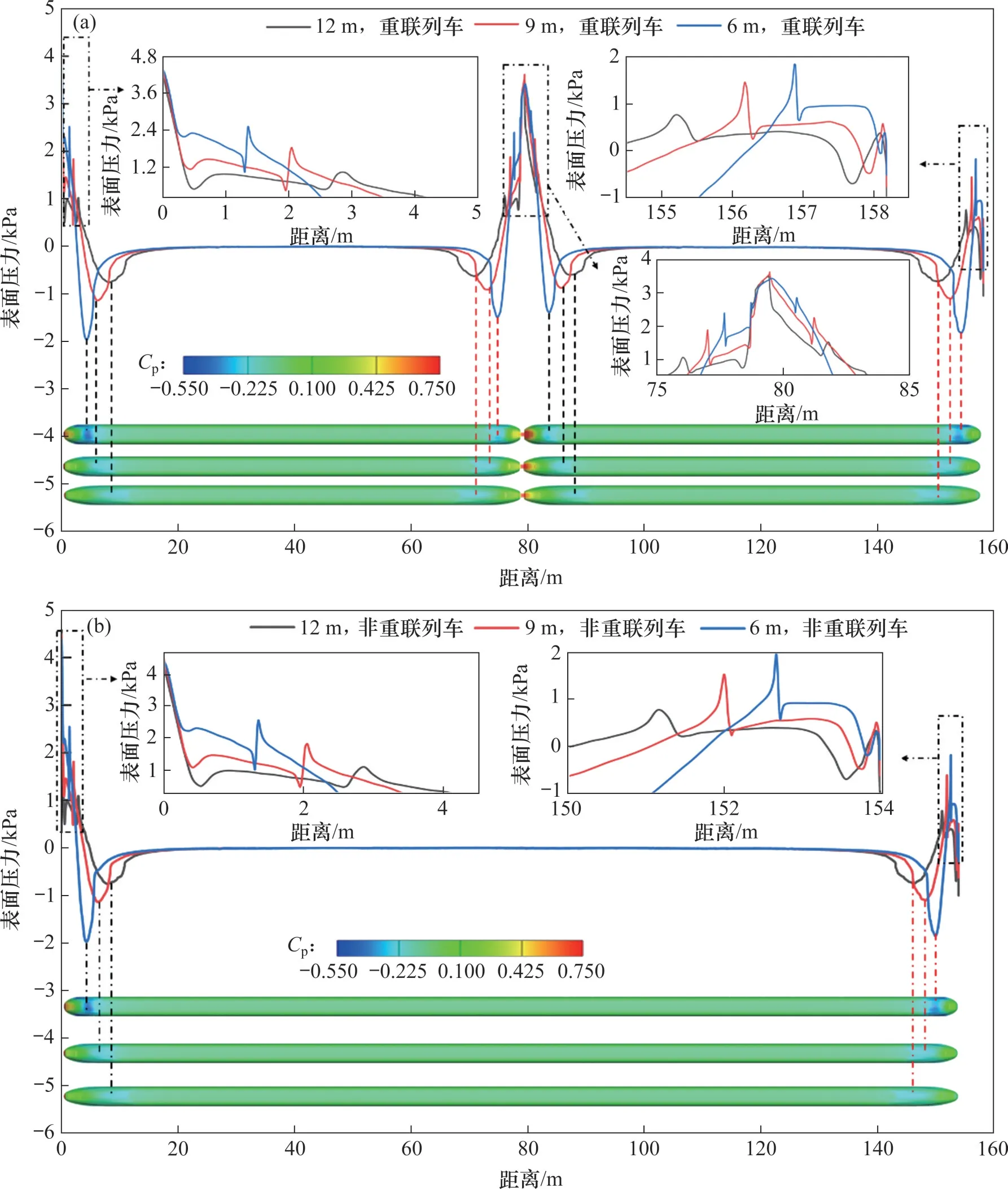
图13 列车纵剖面表面压力变化(300 km/h)Fig.13 Variation of car body surface pressure along longitudinal symmetry line(300 km/h)
1)流线型长度越长,列车表面压力越小。
2)流线型长度越长,列车表面压力变化程度越平缓。
观察图13 可知:流线型长度对表面压力的影响十分显著,但影响范围仅限于头车和尾车的流线型区段内。当压力曲线每次发生突变时,波峰均对应列车的鼻尖处,波谷则对应头车或尾车的流线型末端与平直车顶的交接处。此外,由于司机室挡风玻璃为嵌入型,受连接处凹槽结构的影响,在波峰和波谷之间,压力会发生小范围突变。
4 结论
1)受重联区域特殊结构的影响,在相同运行条件下重联列车的总阻力要明显大于非重联列车的总阻力。但是,随着流线型长度增加,2种列车在相同环境下运行时的气动阻力差距逐渐减小。
2)重联列车通常由2 列完全相同的列车组成,故前后2列列车车体表面压力分布具有相同的规律性,但在数值上存在明显差异。位于重联区域车钩后方的头车(H2),其车体表面压力要大于前方头车(H1)的表面压力,而尾车表面压力分布情况则与之相反。随着流线型长度增加,后方头车(H2)的气动阻力系数特性逐渐向前方头车(H1)靠拢,前方尾车(T1)的阻力系数则逐渐接近后方尾车(T2)的阻力系数。
3)从整体的角度看,增加流线型长度能够更有效地提升重联列车的气动性能。从单一车辆的角度来看,重联区域与车钩相连的前后两节车辆的气动特性有显著差别,流线型长度增加,车钩前方相邻车辆的阻力逐渐增大,升力逐渐降低;车钩后方相邻车辆的阻力逐渐降低,升力绝对值逐渐增加。

