西部铁路特殊地段轨道结构适应性研究

向俊，彭子祥，杨海明，袁晓利，潘靖凯，梁洁林

(中南大学 土木工程学院，湖南 长沙，410083)

我国西部铁路具有陡峻的高原地形、强烈的板块活动、频发的地质灾害、脆弱的生态环境、恶劣的气候条件等环境特征。目前，关于西部铁路到底采用何种轨道结构类型，特别是在一些轨道基础有可能发生大变形的特殊地段(如不均匀沉降地段、路基冻胀上拱地段、活动断裂带等)尚没有定论，而西部铁路建设正在如火如荼地进行，因此，亟需对西部铁路特殊地段轨道结构的选型进行研究。

西部铁路的轨道结构除了应满足一般的设计原则与规范外，还需要重点注意在长期运营过程中的维修性，原因在于它将穿越活动断裂带及局部无人区，频发的地质灾害与季节性冻土将不可避免地引起轨道基础的大变形，高原缺氧又加剧了养护维修作业环境的恶劣性，因此，西部铁路的轨道结构应具备少维修、易调整、可快速维修的基本功能[1]。

一般地，轨道结构分为有砟及无砟轨道，刘杰[2]在对西部铁路轨道选型与设计分析中，根据经验，提出了一些建议性方案：对于西部铁路一般地段，推荐采用双块式无砟轨道；对于活动断裂带等线下基础变形难以控制的区域，建议采用便于调整的有砟轨道，但对于有砟道床，采取胶结、固化等措施，以降低运营期养护维修工作量。这种对有砟道床进行胶结、固化的轨道结构，就是最近10年来我国发展起来的聚氨酯固化道床轨道结构，其性能处于有砟与无砟轨道性能之间，具有足够的强度和稳定性，并兼有混凝土整体道床残余累积变形缓慢和散粒体碎石道床弹性好、可维修性好的优点，能显著减少养护维修工作量，是一种极具发展前景的新型轨道结构形式，特别适合在线下基础产生复杂变形的特定地段进行铺设[3-5]。但针对刘杰[2]提出的建议性方案未见进一步研究成果，为此，本文结合西部铁路一些特殊地段相关条件，对聚氨酯固化道床轨道静力特性进行研究。鉴于轨道不平顺直接影响到列车运行品质[6]，而轨道基础的大变形将会映射到轨面，形成轨面不平顺[7]，还会产生离缝现象[8]，大大影响了轨道结构的维修性，本文重点研究聚氨酯固化道床轨道在基础大变形作用下的轨道结构变形、影响规律及其维修特性，同时，与双块式无砟轨道结构的计算结果进行对比分析，以便深入了解西部铁路特殊地段轨道结构的适应性。

我国自2009年开始铺设聚氨酯固化道床轨道试验段以来，王红等[4,9-11]通过室内外试验及仿真计算，对聚氨酯固化道床累积变形力学行为及荷载传递规律等基本力学性能进行了研究；孔凡兵等[12-16]对聚氨酯固化道床轨道的动力特性进行了分析。但西部铁路轨道基础可能发生大变形的特殊地段，人们对聚氨酯固化道床轨道的力学特性分析较少。

双块式无砟轨道主要应用于我国，且跨越东西南北，各地工程地质及环境特征迥异，因此，有关此种轨道在一些特殊地段上的力学特性分析是目前的研究热点之一。赵国堂[17]基于地基沉降变形机理及无砟轨道各结构层间关系的处理，研究了路基变形作用下高速铁路无砟轨道-路基变形计算模型的合理性，并分析了路基变形对无砟轨道层间离缝及支承层产生的拉应力的影响规律。蔡小培等[18]基于有限元方法探讨了地面不均匀沉降幅值、范围及形式与双块式无砟轨道平顺性间的关系；郭宇等[19]分别采用解析法与数值法分析了不均匀沉降与双块式无砟轨道轨面变形间的关系。张永斌[20]针对兰新高速铁路分析了路基冻胀对双块式无砟轨道静动力特性的影响，并对路基冻胀变形管理限值进行了探讨。

本文首先采用ABAQUS 有限元软件，分别建立聚氨酯固化道床轨道与双块式无砟轨道的计算模型，并进行验证；其次，对比探究这2种轨道结构在基础不均匀沉降、上拱及断层作用下的变形规律及其维修性；最后，基于变形规律及其维修性，对这2种轨道在西部铁路特殊地段的适应性进行综合分析，旨在为西部铁路特殊地段轨道结构的选型提供参考。

1 模型的建立及其验证

1.1 有限元模型的建立

据铁路相关管理部门统计，迄今为止，我国高速铁路铺设的无砟轨道总里程中，双块式无砟轨道所占比例已超过50%，鉴于双块式无砟轨道结构较普及，这里对聚氨酯固化道床轨道结构进行研究。

聚氨酯固化道床轨道结构形式有枕下全断面浇筑和轨下双梯形浇筑断面2 种[3-5]。我国主要采用轨下双梯形断面，具体由钢轨、扣件、轨枕和聚氨酯固化道床等部件组成，其中，聚氨酯固化道床又包含道砟粘结区域及道砟未粘结区域，同时，轨枕与双梯形断面一并粘结在一起，如图1所示，本文采用此结构进行建模计算。

图1 聚氨酯固化道床轨道结构示意图Fig.1 Schematic diagram of polyurethane-cured track structure

ABAQUS 软件在结构计算中具有强大功能，本文采用此软件对聚氨酯固化道床轨道及双块式无砟轨道分别建模，如图2所示。建模中的几个主要环节如下：钢轨均模拟为点支承的空间梁单元；扣件均采用连接器单元模拟；前者中的轨枕、聚氨酯固化道床及基础以及后者中的双块式轨枕、道床板、支承层及基础均采用实体单元模拟，聚氨酯固化道床不同区域考虑不同材料属性。为模拟2种轨道结构在不同基础变形作用下产生的离缝或脱空现象，在固化道床与基础之间以及支承层与基础之间均设置为摩擦接触。为了消除边界影响，同时考虑计算效率并结合文献[14,21]中的计算方法，将模型纵向长度均取65 m。有关模型中的主要计算参数参见文献[14,21]。

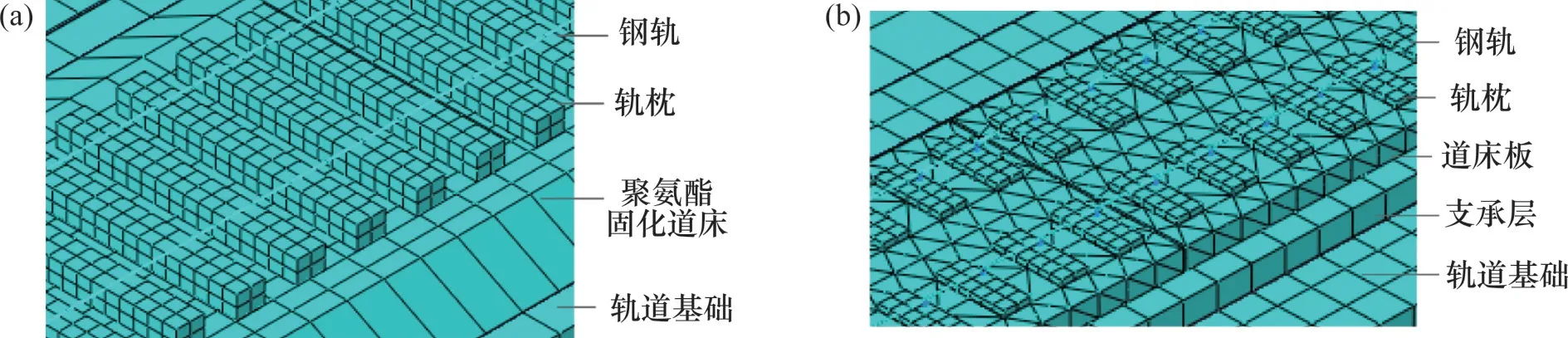
图2 2种轨道有限元模型Fig.2 Finite element models of two tracks

1.2 模型的初步验证

采用图2(a)中的模型及文献[14]中的参数与计算工况，计算聚氨酯固化道床轨道的竖向位移，并与文献[14]中的计算结果进行比较，见表1。由表1 可知：钢轨竖向位移计算结果的相对误差为7.9%，道床竖向位移计算结果的相对误差为5.0%，可见，相对误差均很小。

表1 聚氨酯固化道床轨道竖向位移计算结果Table 1 Calculation results of vertical displacements of polyurethane-cured track mm

采用图2(b)中的模型及文献[21]中的参数与计算工况计算双块式无砟轨道的竖向位移，并与文献[21]中的计算结果进行比较，见表2。由表2 可知：与文献[21]中的结果相比，钢轨竖向位移计算结果的相对误差为5.9%，道床板竖向位移计算结果的相对误差为9.1%，支承层竖向位移计算结果的相对误差为12.5%。

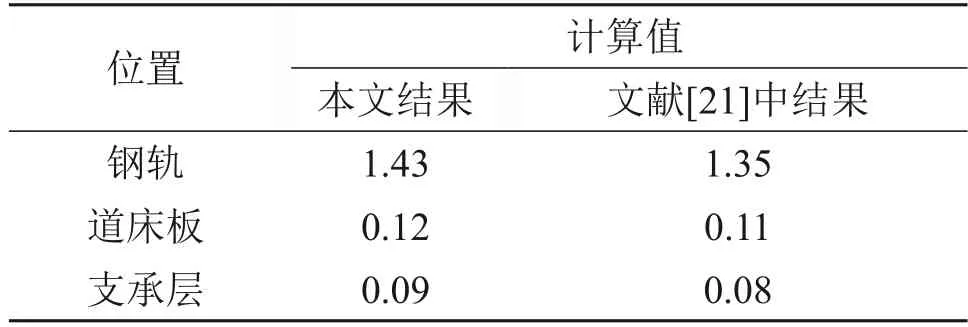
表2 双块式无砟轨道竖向位移计算结果Table 2 Calculation results of vertical displacements of double-block ballastless trackmm

综上所述，对于轨道竖向位移，本文计算结果与文献[14,21]中的结果基本一致，初步验证了本文计算模型是可靠的，可用于后续的轨道变形计算。

2 基础变形作用下2 种轨道结构的位移与离缝比较

轨道基础变形(如路基不均匀沉降、冻胀上拱、活性断层等)将映射为轨面不平顺，进而直接影响行车品质，还将产生轨道结构与基础之间的离缝现象。轨道结构离缝的存在不但影响行车品质，而且将直接影响轨道结构的强度及耐久性，加速轨道结构的破坏，从而进一步影响轨道结构的维修。为此，本文选择钢轨位移及离缝这2 项指标，对聚氨酯固化道床轨道及双块式无砟轨道在基础变形的特殊地段的适应性进行比较。

2.1 基础不均匀沉降作用下的比较

根据规范[22]，本文考虑的轨道基础不均匀沉降模型如图3所示，并采用式(1)加以描述。

图3 余弦型不均匀沉降曲线Fig.3 Cosine type curve of settlement

式中：y为沉降幅值；z-z0为任意沉降位置与沉降起点之间的距离；f0为沉降峰值；L为沉降波长。为了便于对计算结果进行观察，纵坐标取向下为正。

参照文献[17-19]，具有代表性的沉降波长L分别取5～40 m，级差为5 m；相应的沉降峰值f0分别取5～20 mm，级差为5 mm。计算时，将路基不均匀沉降峰值置于计算模型长度的中点，然后，基于前述所建立的2种轨道计算模型，分别计算在上述路基不均匀沉降作用下，这2种轨道结构中钢轨竖向位移最大值随波长及幅值的变化规律，如图4所示，有关这2种轨道结构离缝最大值随波长及幅值的变化规律如图5所示。

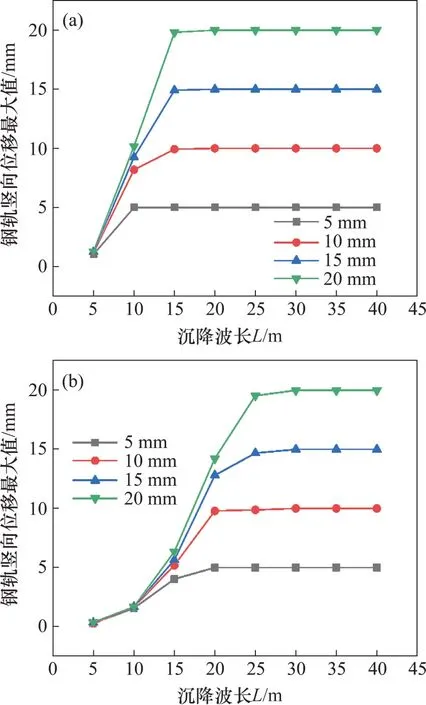
图4 钢轨竖向位移最大值随沉降波长与幅值的变化规律Fig.4 Variation of the maximum vertical displacement of rail with wavelength and amplitude of settlement

图5 离缝最大值随沉降波长与幅值的变化规律Fig.5 Variation of the maximum seam value with wavelength and amplitude of settlement

从图4(a)及图5(a)可见：对于聚氨酯固化道床轨道，当沉降波长L＜15 m 时，钢轨竖向位移最大值随着L的增大迅速增大，离缝最大值则随着L的减小而快速增大；当L≥15 m 时，钢轨竖向位移最大值基本上达到了各自对应的沉降峰值，而离缝值则均趋近于零。

从图4(b)及图5(b)可见：对于双块式无砟轨道，当沉降波长L≤25 m 时，钢轨竖向位移最大值随着L的增大呈增大趋势，离缝最大值则随着L的减小而急剧增大；当L＞25 m 时，钢轨竖向位移最大值基本上达到了各自对应的沉降峰值，而离缝值则均趋近于零。

上述现象表明：沉降波长越大，钢轨竖向位移越大，而离缝值越小；沉降波长越小，钢轨竖向位移越小，离缝值则越大。换言之，沉降波长越大，轨道结构与基础之间的跟随性越强，沉降波长越小，轨道结构越容易与基础之间发生分离。

当15＜L＜25 m时，这2种轨道钢轨竖向位移及离缝值差异较大。以L=20 m、f0=20 mm 为例，这2种轨道钢轨竖向位移及离缝分布情况如图6所示。从图6可见：聚氨酯固化道床轨道随基础变形的跟随性远强于双块式无砟轨道随基础变形的跟随性。

图6 不均匀沉降作用下两种轨道变形及离缝分布图(L=20 m，f0=20 mm)Fig.6 Distribution diagram of deformation and seam of two tracks under the action of uneven settlement(L=20 m，f0=20 mm)

2.2 基础冻胀引起的上拱作用下的轨道变形比较

根据文献[20,23]，本文考虑的轨道基础冻胀引起的上拱模型如图7所示。为了便于对计算结果进行观察，纵坐标取向上为正，其线形也可采用式(1)加以描述，但需注意纵坐标的正负号。

图7 余弦型上拱曲线Fig.7 Cosine type curve of the frost heave

计算结果表明：上拱作用下的轨道竖向变形及其与基础间的跟随性完全不同于沉降作用下的结果。以L=20 m、f0=20 mm 的上拱工况为例，这2种轨道钢轨竖向位移及离缝分布如图8所示。

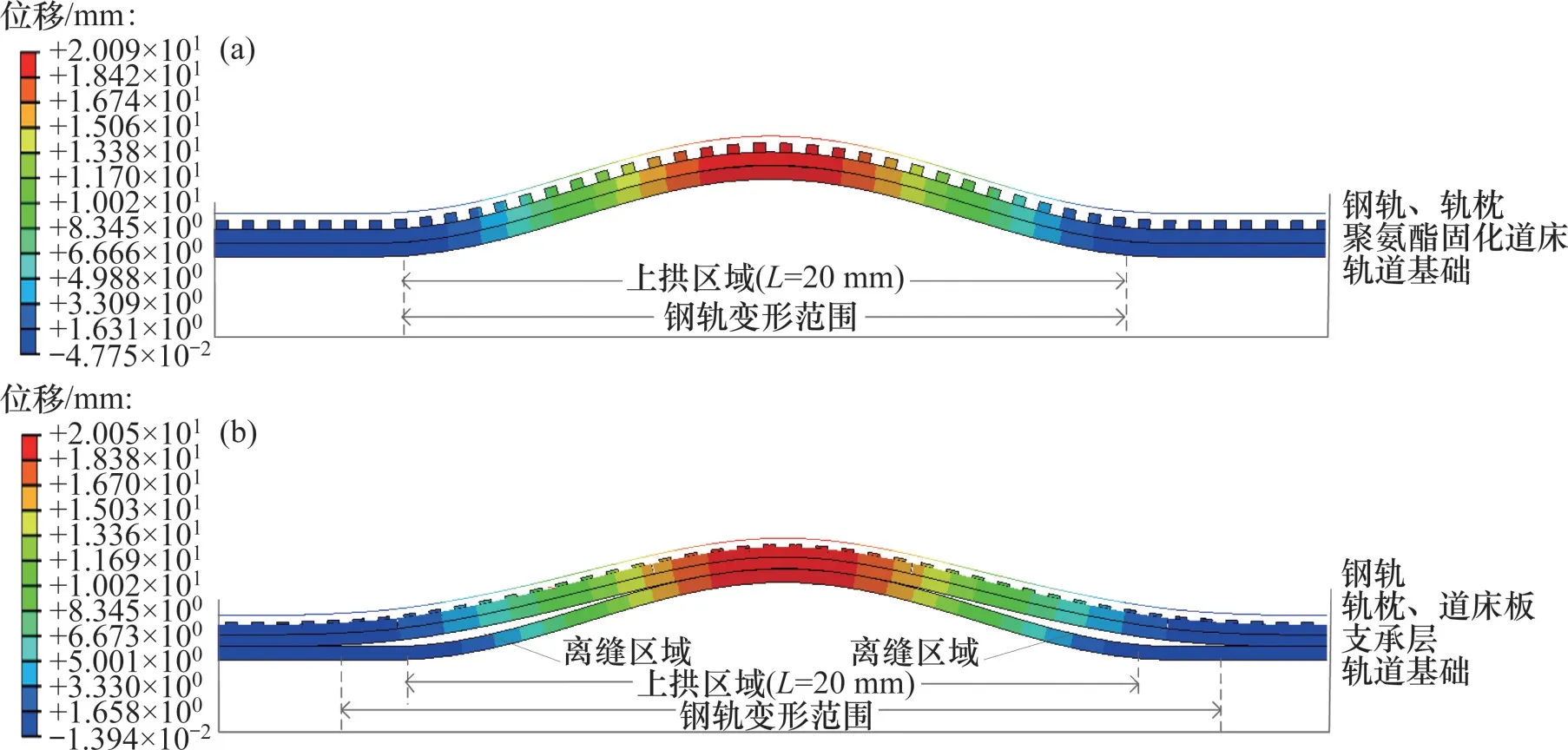
图8 冻胀上拱作用下两种轨道变形及离缝分布Fig.8 Distribution of deformation and seam of two tracks under the action of frost heave

由图8可见：相对于双块式无砟轨道，聚氨酯固化道床轨道与基础间的跟随性更加明显；离缝最大值不再位于上拱峰值处，整个离缝区域位于上拱峰值的两侧，且存在一定距离，这样，导致2种轨道最大竖向位移几乎相当。

参照文献[20,23]，具有代表性的上拱波长L取5～40 m，级差为5 m；相应的上拱峰值f0取5～20 mm，级差为5 mm。计算时，将上拱峰值置于计算模型长度的中点处，然后，基于1.1节所建立的2种轨道计算模型，分别计算上拱作用下2种轨道结构中钢轨竖向位移最大值随波长及幅值的变化规律，如图9所示；2 种轨道结构离缝最大值随波长及幅值的变化规律如图10所示。

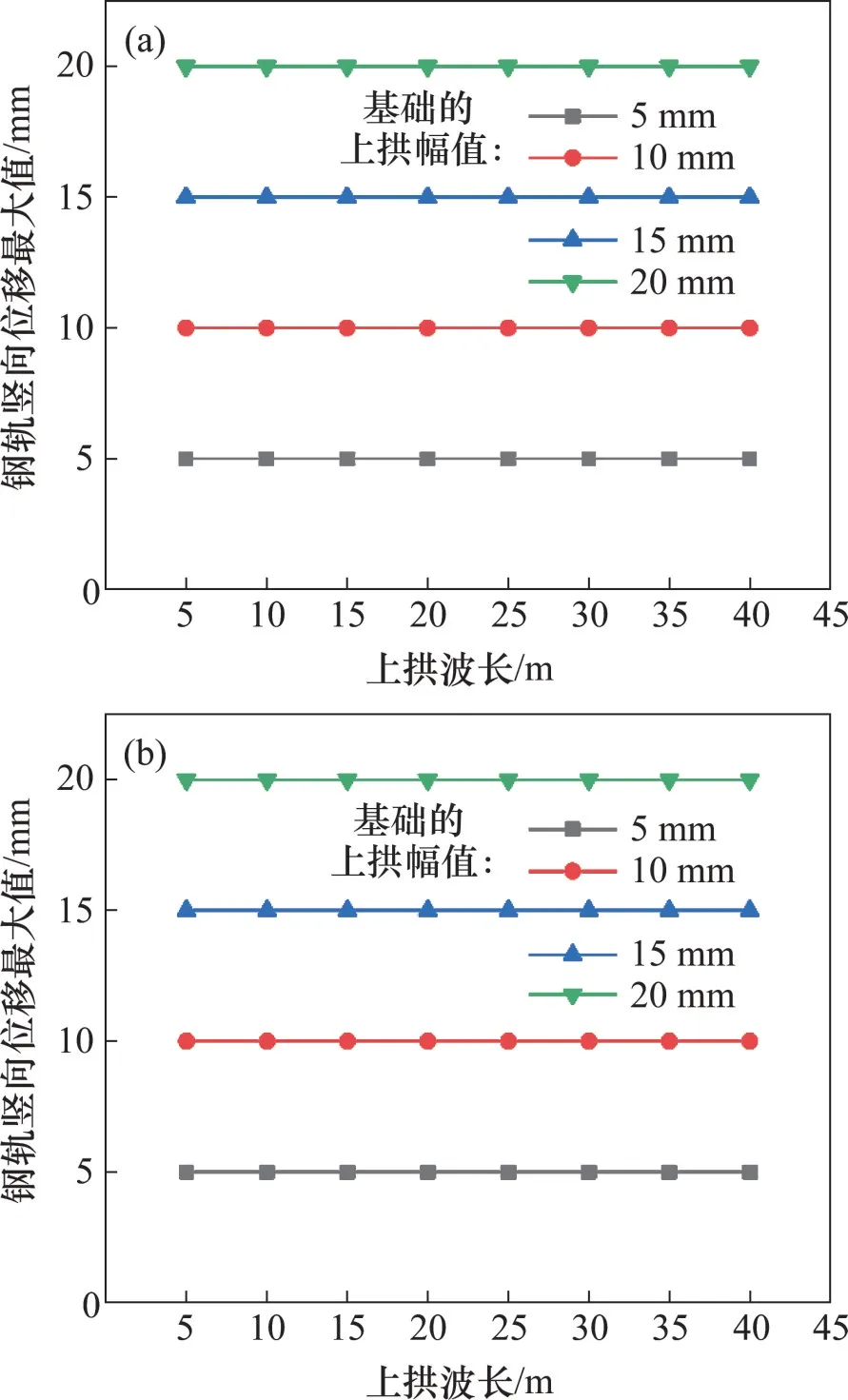
图9 钢轨竖向位移最大值随上拱波长与幅值的变化规律Fig.9 Variation law of the maximum vertical displacement of rail with wavelength and amplitude of upper arch

图10 离缝最大值随上拱波长与幅值的变化规律Fig.10 Variation law of the maximum seam value with wavelength and amplitude of the upper arch

从图9和图10可见：

1)这2种轨道竖向位移最大值均接近于各自对应的上拱峰值，表示在上拱峰值处，这2种轨道随基础上拱的跟随性均很强，从而出现了与峰值相当的钢轨竖向位移最大值。

2)对于聚氨酯固化道床轨道，当上拱波长L＜20 m 时，离缝最大值则随着L减小而呈缓慢增大趋势，且离缝最大值很小；当L≥20 m 时，离缝值则趋近于零。

3)对于双块式无砟轨道，当上拱波长L＜35 m时，离缝最大值随着L的减小呈增大趋势，上拱波长越小，离缝最大值增大越急剧；当L≥35 m时，离缝值则趋近于0。

4)在基础上拱作用下，2种轨道的钢轨竖向位移均出现了与上拱峰值接近的最大值，说明这2种轨道均会出现接近上拱峰值的最大轨道不平顺值；相对于双块式无砟轨道，在上拱作用下，聚氨酯固化道床轨道随上拱变形的跟随性很强，即使在波长不大的上拱作用下出现了离缝现象，其量值也很小。

2.3 活性断层作用下的轨道变形比较

西部地区具有显著的地形地貌差异，在高原与盆地过渡地带形成若干活跃断裂带，控制着西部铁路沿线地形地貌，这对西部铁路的跨越产生直接影响[24]。断层是岩层或岩体沿破裂面发生明显位移的构造形式，发生断层的地方会在断层面两侧形成2个岩块。断层分正断层及逆断层，对于正断层，位于断层面以上的岩块叫上盘，位于下部的叫下盘，根据文献[12]，本文考虑的正断层计算模型如图11所示。图11中，O1为从没有发生断层的O处沿断层面移位而来。以O为坐标原点，建立坐标系。θ表示断层倾角，v表示竖向位移(即竖向错动量)，u表示纵向位移。可见，若已知v与θ，则可求得u，根据文献[25]，本文θ取45°。为了便于对计算结果进行观察，纵坐标取向上为正。

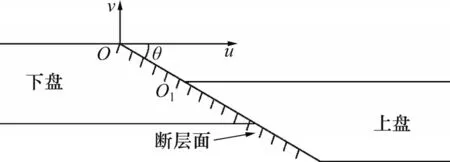
图11 正断层计算模型Fig.11 Calculation model of normal faultage

为了从宏观上把握断层作用下的轨道变形及离缝的分布情况，以v=20 mm、θ=45°为例，计算在正断层作用下聚氨酯固化道床轨道及双块式无砟轨道的变形及离缝分布，如图12所示。由图12可见：这2种轨道结构均出现了离缝现象，且离缝形状类似于正断层的线形，相对聚氨酯固化道床轨道而言，双块式无砟轨道所产生的离缝幅值及范围均要大；在正断层附近，上盘上的轨面比下盘上的轨面低，从而轨面呈坡面形状。

图12 正断层作用下两种轨道变形及离缝分布图(θ=45°，v=20 mm)Fig.12 Distribution diagram of deformation and seam of two tracks under the action of normal faultage(θ=45°,v=20 mm)

为了进一步了解这2种轨道变形及离缝随正断层的变化规律，计算时，取θ=45°，根据文献[12,25]，竖向错动量v取5～20 mm，级差为5 mm，分别计算聚氨酯固化道床轨道及双块式无砟轨道中钢轨竖向位移随错动量的变化规律，如图13所示。这2种轨道结构离缝最大值和离缝随错动量的变化规律如图14所示。

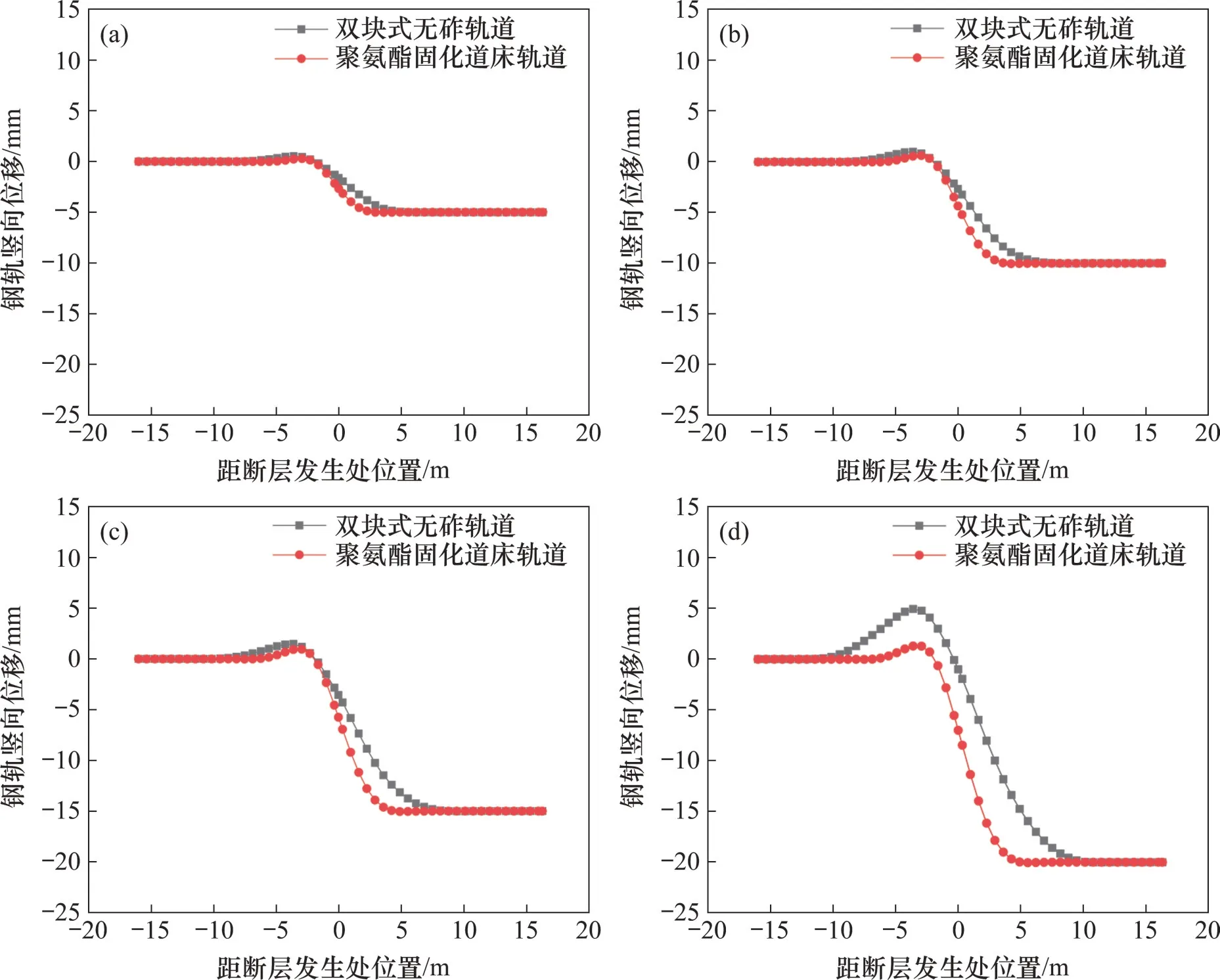
图13 2种轨道钢轨竖向位移随正断层的变化规律Fig.13 Variation law of vertical displacement of rails of two tracks with normal faults

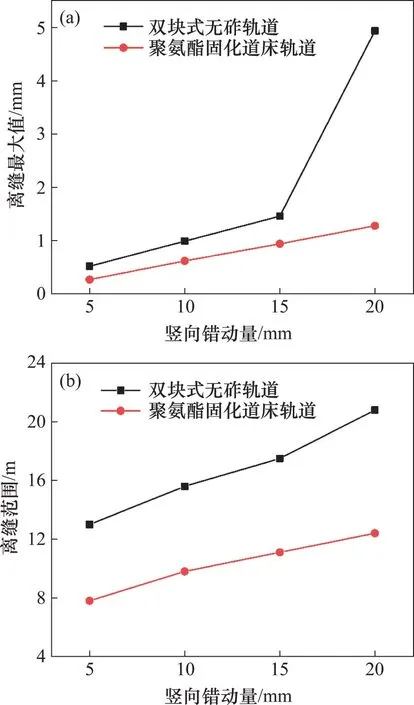
图14 2种轨道离缝最大值及范围随正断层的变化规律Fig.14 Variation law of the maximum and range of two tracks seam value with normal faults

从图13 可见：这2 种轨道中钢轨竖向位移幅值及其变形范围均随断层错动量的增大而增大；所造成的钢轨前后高低幅值基本上与错动量的幅值接近；相对于双块式无砟轨道，聚氨酯固化道床轨道中的钢轨竖向位移更大，而变形范围更小，说明聚氨酯固化道床轨道随断层的跟随性更强。

从图14 可见：这2 种轨道离缝最大值及离缝范围均随错动量的增大而增大；相对于聚氨酯固化道床轨道，双块式无砟轨道所产生的离缝幅值及范围均较大；当错动量v=20 mm 时，离缝值出现了急剧变化，此时，双块式无砟轨道出现的最大离缝值为4.94 mm，离缝长度为20.80 m，而聚氨酯固化道床轨道出现的最大离缝值仅为1.28 mm，离缝长度为12.40 m。

上述现象表明，在正断层作用下，一方面，氨酯固化道床轨道会产生更大的钢轨竖向位移，但离缝最大值及其范围更小；另一方面，双块式无砟轨道中的钢轨竖向位移较小，但离缝最大值及其范围更大。

3 轨道基础变形地段2 种轨道结构的维修性比较

本文主要针对西部铁路不均匀沉降、上拱、断层等引起轨道基础大变形的特殊地段，探讨聚氨酯固化道床轨道及双块式无砟轨道面临的问题及其维修方法，通过比较分析，对2种轨道的适应性加以分析，以便为西部铁路特殊地段轨道选型提供参考。

本文考虑的路基不均匀沉降、上拱及断层等西部铁路特殊地段引起的轨道基础变形幅值及范围一般都较大，将会引起较大幅值及范围的钢轨竖向位移与离缝。一方面，较大幅值的钢轨竖向位移将直接作用于轮轨界面，加剧车-轨振动响应，从而影响列车运行舒适性，甚至威胁行车安全[6-7,19]；另一方面，较大幅值的离缝除了影响列车运行品质外，在过往运营列车反复作用下，离缝上下层之间将产生“拍打”效应，加剧轨道结构本身破坏，属于轨道典型病害之一[26]。由此可见，一旦出现路基不均匀沉降、上拱及断层等引起的轨道变形及离缝现象，必须加以维修，恢复线路正常状态，确保列车正常运行。

当轨道不平顺幅值不大时，聚氨酯固化道床轨道及双块式无砟轨道维修方法一般采用扣件调整量来恢复轨面的平顺性。最大调整量主要取决于扣件的调整量，如在高速铁路无砟轨道扣件中[27]，WJ-7型、WJ-8型、W300-1这3种扣件的最大调整量均为-4～+26 mm，其中负号表示调低量，正号表示调高量，SFC 型扣件的最大调高量为+30 mm，而聚氨酯固化道床轨道匹配的弹条V 型扣件的最大调高量则达50 mm[28]。可见，这2种轨道的扣件肯有一定的调整能力，相对而言，聚氨酯固化道床轨道的扣件调整能力更强。

当双块式无砟轨道出现的离缝不大时，可采用填充树脂材料，或者采用注浆方式来消除离缝。当双块式无砟轨道出现的离缝较大时，仅仅靠填充材料或注浆不能完全解决问题，此时，需要采用锯板断道，进行重新施工，重新调整轨道几何形位，以满足无砟轨道平顺性之要求[29]。当双块式无砟轨道不平顺或离缝幅值过大、采用常规方法仍不能满足要求时，则需要对轨道基础进行重新调整，最终满足平顺性要求。但需注意的是，这种对双块式无砟轨道基础进行重新调整的维修方法实施起来相当困难。为此，陈秀方等[30]认为，无砟轨道结构形式应视工程环境条件及线下工程类型等因素综合权衡确定，在活动断裂带、地面严重沉降区、冻结深度较大且地下水位较高的季节冻土区以及深厚软土等区域变形不易控制的特殊地质条件地段，不宜采用无砟轨道。双块式无砟轨道对于西部铁路特殊地段适应性很差。

当聚氨酯固化道床轨道出现大幅值的轨道不平顺或离缝时，即使超出了扣件调整能力，也仍然具有灵活便利的维修方法[28]，表现在：1)采用小型门吊将沉降范围内的聚氨酯固化轨枕块整体吊出，更换为更大固化道砟厚度的聚氨酯轨枕块；2)采用小型门吊将沉降范围内的聚氨酯轨枕块吊起，在块下填充速凝混凝土或树脂材料进行调整修复。实际上，聚氨酯固化道床轨道兼具了有砟轨道便于调整和无砟轨道少维护且稳定性好的优点，已证明可以有效解决有砟-无砟轨道过渡段病害较严重的问题[31]，成为继有砟轨道和无砟轨道之后的第三种轨道结构形式。目前，此种轨道已实现预制装配化[32-33]，它不仅具有道床结构少维护、运营期不用进行道床捣固及清筛等大机作业等优势，而且可以实现基础沉降后的单元化维修。

综上所述，相对于双块式无砟轨道，聚氨酯固化道床轨道对工程及环境条件恶劣的西部铁路维修作业更具有适应性。

4 结论

1)基于ABAQUS 软件，分别建立了聚氨酯固化道床轨道与双块式无砟轨道计算模型，并进行了验证，结果表明，所建立的计算模型正确、可靠，可以进一步用于轨道基础大变形作用下2种轨道的静力分析。

2)在路基不均匀沉降作用下，2种轨道结构都出现了幅值较大的钢轨竖向位移或离缝，且最大幅值均出现在沉降峰值位置。当沉降波长较小时，离缝峰值变大，并趋于沉降峰值，而钢轨竖向最大位移变小，并趋于零；当沉降波长较大时，离缝峰值变小，并趋于零，而钢轨竖向最大位移变大，并趋于沉降峰值。可见，沉降波长越小，2种轨道与路基不均匀沉降的跟随性越差；沉降波长越大，2种轨道与路基不均匀沉降的跟随性越好。

3)在路基上拱作用下，2种轨道结构都出现了最大值接近上拱峰值的钢轨竖向位移，且均出现在上拱峰值位置；而离缝现象则均出现在上拱波长两端附近。当上拱波长较大时，离缝峰值变小，并趋于零；当上拱波长较小时，离缝峰值均变大，但聚氨酯固化道床轨道的离缝值要远小于双块式无砟轨道的离缝值，说明聚氨酯固化道床轨道与路基上拱变形的跟随性更强。

4)在断层作用下，2种轨道结构均会产生钢轨竖向位移及离缝现象。双块式无砟轨道的钢轨竖向位移小于聚氨酯固化道床轨道的钢轨竖向位移，而双块式无砟轨道的离缝值及其范围远大于聚氨酯固化道床轨道的离缝值及其范围，这也说明聚氨酯固化道床轨道随断层的跟随性更强。

5)聚氨酯固化道床轨道对工程及环境条件恶劣的西部铁路的维修作业具有更好的适应性。