基于场路结合的微波加热系统等效电路模型

杨彪，苏森涛，马亦骥，倪瑞璞，曾德明，肖青云，王银双

(1.昆明理工大学 信息工程与自动化学院，云南 昆明，650500；2.昆明理工大学 云南省人工智能重点实验室，云南 昆明，650500；3.昆明理工大学 非常规冶金教育部重点实验室，云南 昆明，650093)

微波加热是一种新型的绿色冶金方法，媒质内部的介电损耗直接将微波能量选择性地传递给被加热媒质的分子或原子，宏观上表现出加热可选择性、加热均匀、热效率高、清洁无污染等特点[1-3]。微波加热过程是高频电磁波与媒质相互作用的动态响应过程。电磁场分布在微波应用器腔体内部，随着电磁波的传播微波能，媒质热量积累、温度上升、载流子运动，而温度变化和载流子运动又使得媒质的介电常数和电导率等物理参数发生改变，反过来影响电磁场分布，最终这些变化会造成加热媒质状态发生变化、应用器加热效能降低，甚至造成应用器加热失效[4-5]。

了解高频电磁波与媒质相互作用的响应过程是优化控制加热过程与提高应用器效能的关键，但由于该复杂响应过程涉及电磁场、热传导和载流子运动多种物理过程，必须联立电磁场方程、热传导方程和载流子方程，构建多物理场方程组，从而进行计算，但是计算难度大。因此，找到分析高频电磁波与媒质相互作用的响应过程的方法十分必要[6-7]。

微波应用器内高频电磁波的场分布问题一般归结为求解边值问题。求解电磁分布边值问题通常用全波场分析方法，主要有解析法和数值计算方法[8-9]。全波场分析方法计算的结果精确度较高，受到诸多学者的青睐，TANG等[10]基于积分方程理论研究了微小变化的微波频率对的加热均匀性的影响。JING 等[11]用有限差分法计算了微波加热聚烯烃吸收剂混合物时腔体内的问题，得到了腔体内的温度场分布。刘小明等[12]通过有限元方法分析了电磁场、材料介电常数以及导热结构对沥青混凝土传热性能的影响。但是全波场分析方法也存在以下问题：解析法对数学技巧的要求高，求解条件限制多，一般难以直接求解复杂场域和多物理场耦合问题[13]。数值计算方法建模复杂，完成一次仿真计算需要耗费大量时间，缺乏工程实用性[14]。

计算微波加热系统电磁场分布还可以根据传输线理论建立微波加热腔体的等效电路模型，通过等效电路的方法分析微波加热腔体中电磁场的分布。等效电路模型计算简单、计算速度快。WU等[14]研究微波加热热失控温度与电场强度之间的“S 曲线”关系时，基于单模波导理论建立了微波加热谐振腔等效电路模型。但是通过等效电路模型直接计算微波加热问题，腔体内电磁波吸收和反射的情况被忽略，计算精度不高。亟需一种既保持等效电路模型计算速度又提高等效电路模型计算精度的计算方法。场路结合方法通过三维的全波场分析仿真，获得相对精确的二维电路分析模型的参数，并将这些参数代入二维电路模型中用于计算，从而在保持电路分析快速性的前提下提高电路分析精确性[15]。场路结合方法在很多领域都有应用，王大朋等[16]通过场路结合的方法分析了磁轴承的悬浮力，利用磁路法推导了磁轴承悬浮力的线性化模型。毛煜茹等[17]分析微波通信系统非线性金属结的无源互调干扰时，运用场路结合的方法精确地计算了由于金属接触非线性引起的无源互调及其作为二次辐射源所激发的电磁场。

综上所述，在分析微波加热动态响应过程时，全波场分析方法精度高，等效电路方法的计算速度快。本文提出运用场路结合的方法，分析微波应用器腔体中高频电磁波与媒质之间相互作用的动态响应过程。首先，分析微波加热系统各部分的阻抗特性建立等效电路模型；其次，用全波场分析的方法对应用器腔体各部分进行散射场分析，得到散射参数；然后，将分析得到的散射参数转化为用于等效电路分析的阻抗参数，阻抗参数表征能量的转换；最后，通过等效电路分析计算馈入腔体的微波与媒质之间的能量交换的问题，进而计算出媒质加热温度。

1 微波加热系统相关基础模型

1.1 微波传输等效电路模型

传输线理论在微波系统的分析中有着至关重要的地位，它将对电场和磁场的分析转化为对电压和电流的分析，从而可以将电路理论和网络分析的方法运用到微波系统中[18]。通过传输线理论和传输线方程，可以建立电磁波在含媒质的双端口波导中传播时的等效电压和等效电流关系[19]。

图1所示为一段含任意媒质的波导的二维示意图，设z=0 处媒质两侧区域1 和区域2 无限远处分别有TE10模式的微波沿着波导传向被加热，腔内除被加热介质和空气外无其他媒质。

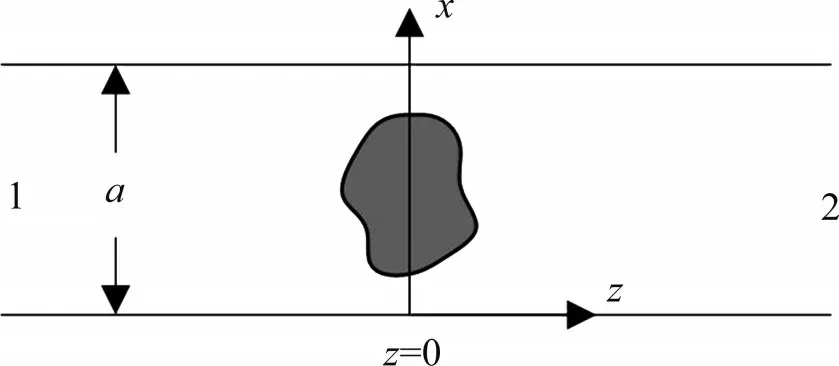
图1 含任意媒质的波导二维示意图Fig.1 Two-dimension diagram of waveguide with arbitrary medium

用U1和I1分别表示媒质左侧从远场到媒质的等效电压和等效电流，U2和I2分别表示媒质右侧从远场到媒质的等效电压和等效电流。由于媒质的存在，媒质两侧U1≠U2，I1≠I2。媒质处的电压和电流的关系可以表示为

即U=ZI，其中：Z为阻抗矩阵，表征微波通过媒质时的损耗，是等效电路分析微波加热时的重要参数。

1.2 微波加热数学模型

微波加热涉及电磁场和传热计算，是Helmholtz方程和Fourier热传导方程的双向耦合。

变化的电场和变化的磁场相互联系、相互激发，组成一个统一的电磁场。电磁场随时间和空间的变化规律可以由麦克斯韦方程表示为：

式中：H为磁场强度，A/m；E为电场强度，V/m；B为磁感应强度，Wb/m2；D为电位移矢量，C/m2；Je、Jm、ρe和ρm分别为电流密度、磁流密度、电荷密度和磁荷密度；σ和σm分别为媒质的电导率和磁导率。

在微波加热谐振腔内的电磁场分布可由式(2)推导的Helmholtz方程表示[3]：

式中：μ0和μr分别为真空磁导率和媒质的相对磁导率；ε0和εr分别为真空介电常数和媒质的相对介电常数；ω为入射微波角频率；k0为自由空间波数；j为虚数单位。

在微波加热过程中，媒质热能来自吸收转化的微波能。通过计算单位体积媒质内的微波耗散功率可以得到热能的热源项，微波的耗散功率可表示为

式中：Q为热源项，表示微波耗散功率；ε″和μ″分别为介电损耗和磁滞损耗。若被加热媒质可忽略磁滞损耗，则可令Qm=0，式(4)可表示为

计算出热源项后，通过以下Fourier 热传导方程计算媒质中热量的产生和传递：

式中：ρ为加热媒质的密度；Cp为加热媒质的比热容；kt为加热媒质的导热系数；T(z，t)为加热媒质的温度。

初始温度条件如下[20]：

温度满足表面热平衡，边界条件可设为[20]：

式中：h为对流换热系数；Tair为媒质周围环境温度；L为媒质厚度。

以式(2)为理论基础，通过式(1)计算得到媒质内部电磁场电场强度，代入式(5)和式(6)可得到加热后媒质的温度。因此，采用全波场分析结合电路的分析方法可以求解微波加热多物理场耦合的问题。

2 场路结合方法的实现

2.1 参数转换

在实际工程应用中，通常使用微波场散射参数S表征微波系统端口的匹配性能和传输损耗。S是反映端口入射波与反射波之间关系的网络参数，在1个二端口网络中，S矩阵包括2个反射系数(S11和S22)与2个传输系数(S12和S21)。其中，S11为端口1 的反射系数，表示端口1 反射波能量与入射波能量的比，S11越小，表示微波能量被反射回源端的能量越少。S21为端口1到端口2的传输系数，表示端口1入射波能量与端口2出射波能量的比，S21越小，表示微波在端口1到端口2传输过程中被吸收的能量越大。

三维全波场仿真获得的S矩阵可以反映媒质对微波的吸收和反射，通过转化为等效电路中阻抗参数矩阵，可以提高等效电路分析微波加热问题的准确度。

根据微波网络原理，波导中媒质部分可以单独看成1个二端口网络，网络两侧等效电压的关系可以表示为

即U-=SU+。其中S为散射矩阵，表示媒质的散射特性，反映了波导中媒质两侧入射波和反射波的振幅的关系[21]。

式中：Ei和Ej分别为波导i和j端口上的激励电场；Ec为相应端口上的总电场。

在第2节中，波导中存在的媒质的阻抗特性由Z表示，反映微波通过媒质时的损耗。阻抗矩阵Z和散射矩阵S从不同的角度反映了波导中媒质对微波传播的影响，2 种特性参数可以通过下式互相转换[22]：

式中：ΔS=(1-S11)(1-S22)-S212。

场路结合构建微波加热等效电路模型如图2所示[22]。

图2 场路结合构建微波加热等效电路模型Fig.2 Microwave heating equivalent circuit model diagram by combining field and circuit

2.2 微波加热系统等效电路模型

微波加热应用器系统一般是由微波发生器、传输波导、控制系统和微波应用器部件组成。为了便于分析微波加热效果，忽略微波发生、传输、控制部分，微波加热系统如图3所示。

图3 微波加热系统示意图Fig.3 Schematic diagram of microwave heating system

假设腔体的腔壁为理想边界，在波传播过程中可以把微波馈入口、媒质、短路端视为波导中的障碍物，计算障碍物的等效阻抗参数，对微波加热系统建立等效阻抗模型，对等效阻抗进行电路变换以及等效可得到如图4所示的电路。图4中I为图3 微波加热系统中的微波源项，Ga为微波源馈入口膜片的损耗和微波源损耗，Gx+jB0为被加热媒质的介电常数和损耗因子，Zd为微波腔体中的传输阻抗，表征回波损耗和传输损耗。

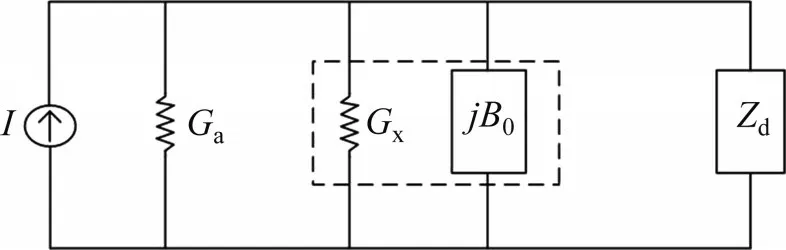
图4 微波加热系统等效电路Fig.4 Equivalent circuit of microwave heating system

媒质的电场与电压呈正比例关系，可将其表示为[14]

式中：k是比例常数。

Gx+jB0可以由阻抗参数表示为[22]

Zd与微波模式、波导波数、腔体尺寸和媒质位置相关，可以表示为

式中：k10为TE10波的波导波数；L1和L2分别表示媒质两侧腔体的长度，与媒质在腔体中的位置以及腔体的长度有关。

对式(13)中的所有量，使用Ga归一化后得到式(16)。

式中：E0为空腔电场幅值；在体积为V的空腔中E0与输入功率P的关系可表示为[23]

结合式(16)和式(17)，媒质部分电压可表示为

式(18)中，变量θ直接影响场路结合算法计算的准确度。运用遗传算法寻优，求出等效电路电源电压与激励电场幅值的误差最小时变量θ的值。遗传算法适应度函数设置为

式中：|Ei|为激励电场幅值。

2.3 场路结合方法算法流程

基于场路结合求解微波加热动态过程算法流程如下：

1)确定微波加热系统模型构成，给定初始条件和边界条件，根据腔体几何模型和加热媒质，划分二端口网络，建立微波加热系统的等效电路模型。

2)应用式(10)～(11)，分析二端口网络的散射场，研究二端口网络各端口的入射波与反射波和出射波的关系，得到二端口网络的散射参数矩阵。

3)应用式(12)将散射参数矩阵转换为用于等效电路分析的阻抗参数矩阵；将步骤1)中设置的微波馈入功率转换为等效电路中电源电压。

4)通过相量法处理步骤3)所得阻抗参数与电源电压之间的相位关系，并把等效后的电源和阻抗参数整合到等效电路模型中。

5)应用式(18)求解电路中媒质部分的电压，并通过遗传算法寻优，以提高所得电压的精度。

6)应用式(13)计算媒质内的电场幅值，并将电场幅值代入式(5)，求出单位体积媒质吸收的微波功率，将吸收功率代入式(6)，求出媒质的温度。

步骤5)中遗传算法寻优的具体步骤如下：

首先，定义遗传算法参数，确定种群大小、最大遗传代数、个体长度、代沟、变异概率、交叉概率、满足条件的适应度范围，初始化种群。

其次，应用式(19)，计算种群中每一个个体的适应度，记录适应度最优的个体。

再次，根据计算的适应度对种群进行随机遍历采样、两点交叉、离散变异操作，产生新的种群，遗传代数增加。

最后，检验适应度是否达到适应度范围条件或者遗传代数是否达到最大遗传代数，如不满足则返回遗传算法寻优步的第二步，如满足则输出最优适应度和对应个体。

3 仿真实验及结果

3.1 微波加热系统模型

微波加热系统模型加热腔体使用长×宽×高为100.0 mm×86.4 mm×43.2 mm 的长方体，波导使用WR340 标准波导。腔体内馈送频率2.45 GHz 的TE10模式波。系统内初始温度设置为20 ℃，微波反应腔壁和波导壁的材料为铜，腔体与波导内介质为空气，被加热媒质为土豆。对需要散射分析的部分用假想参考面进行划分，模型如图5所示[24]。建立模型中应用的初始输入参数设置如表1所示[25]。

表1 模型初始参数设置Table 1 Initial parameter setting of model

图5 微波加热系统模型Fig.5 Model of microwave heating system

边界条件设定的合理性影响仿真结果的准确性。本文的仿真实验中模型的边界条件分为电磁边界条件和热传导边界条件。模型中，腔体壁以及波导壁的材料为铜，其电磁边界条件控制方程为

式中：n为腔壁表面的单位法向量。

热传导边界条件设置为对流热通量，用于计算媒质与周围环境之间的热量交换，定义为如下方程：

式中：∂T/∂n为垂直于温度域表面的温度梯度；h为媒质周围环境的传热系数；T为媒质温度；Tair为媒质周围环境温度；λ为导热系数。

3.2 散射分析模型

为得到加热媒质部分的阻抗参数，需要对微波加热系统模型中包含媒质的二端口网络建立散射参数分析模型，分析模型包括一段含媒质的二端口波导，波导两侧分别设置长×宽×高为61.22 mm×86.40 mm×43.20 mm 的假想区域，其中频率为2.45 GHz 的电磁波在真空中波长的1/2 为61.22 mm。假想区域内介质为空气，用来模拟电磁波从无限远处入射进二端口波导后再出射到无限远处[24]，模型及其右视图如图6所示。

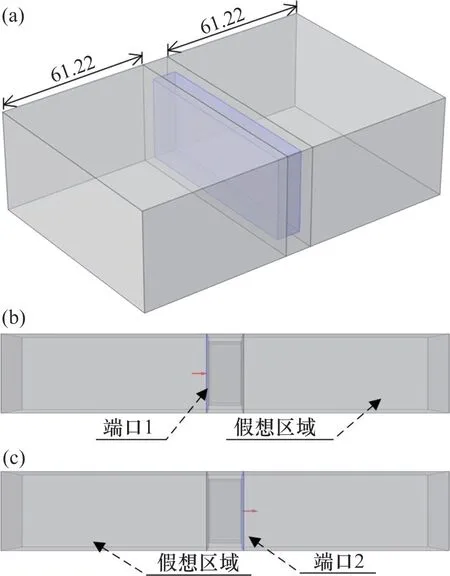
图6 散射分析模型及其右视图Fig.6 Scattering analysis model and its right view

分析二端口波导散射参数时，为保证仿真结果准确性，二端口波导2个端口外假想区域设置散射边界条件，其控制方程为

在微波加热系统中，为了阻止微波加热过程中谐振腔内产生的水气或其他气体、杂质进入波导与磁控管接触，需在微波馈入口位置安装有耐高温、抗腐蚀、良好的透波特性和低损耗特性的介质片，常用的材料有云母、高硼硅玻璃、特氟龙等[26]，分析不同材料在微波馈入口的匹配情况后，选择匹配性能较好的材料作为微波馈入口的介质材料，3 种材料透波性能如图7所示。从图7可见：在电磁波频率为2.45 GHz、介质片厚度为1 mm 的情况下，特氟龙片的透射率最高，可达99.72%，使用1 mm特氟龙片作为微波馈入口介质片微波几乎全功率入射进加热腔体，此时可以忽略微波馈入口反射和吸收的电磁波，即在等效电路中可忽略微波馈入口的阻抗作用。

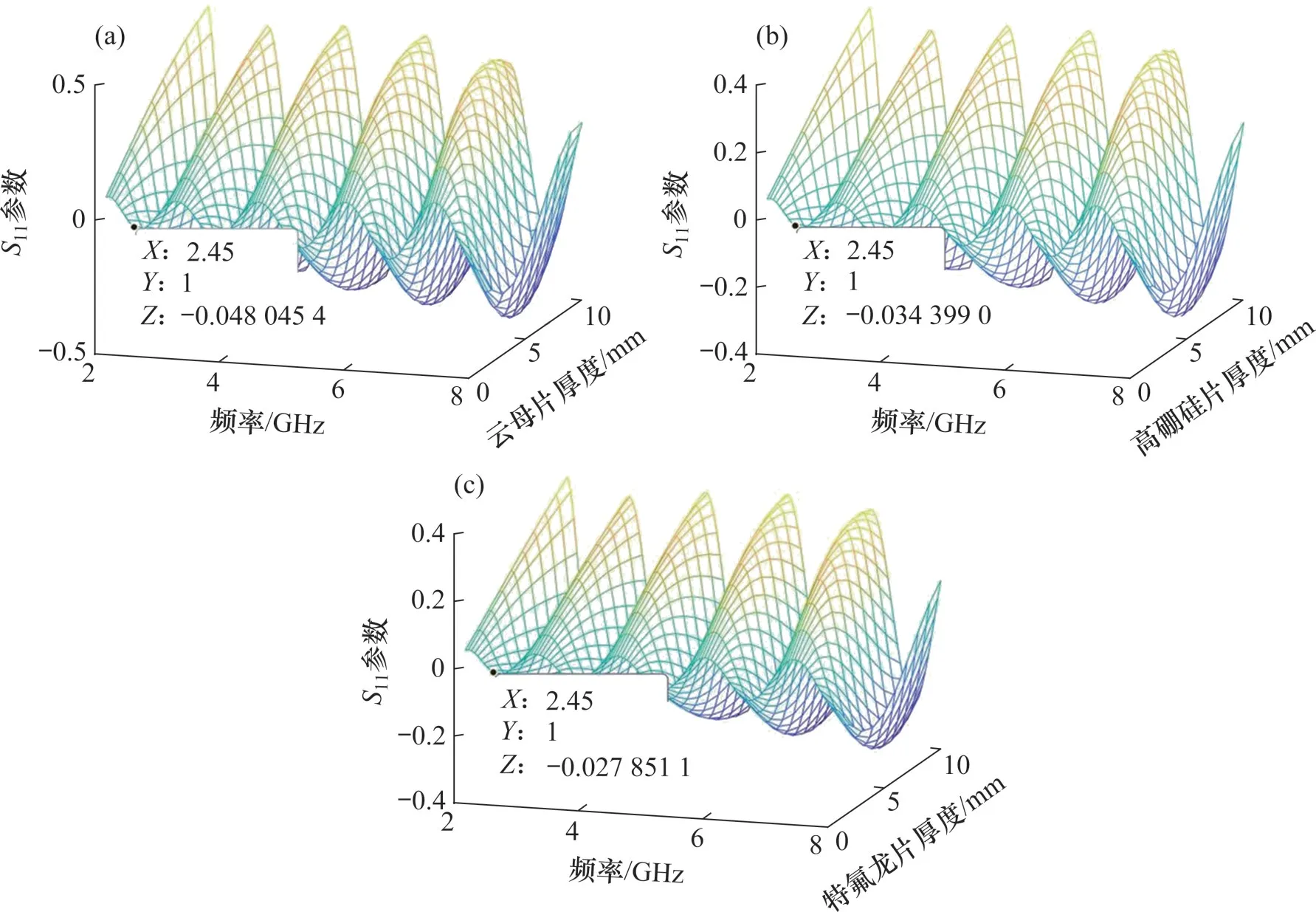
图7 3种材料透波性能Fig.7 Wave transmission properties of three materials

图8所示为对包含长方体媒质的二端口波导进行散射分析时，媒质周围和媒质内部的电场强度分布。由图8可以看出：二端口波导的散射场分析综合考虑了媒质周围电场和媒质内部电场的分布，反映了媒质对微波的吸收和反射作用。本文分析的不同形状不同体积的媒质参数如表2所示。

表2 不同形状媒质尺寸Table 2 Medium size of different shapesmm

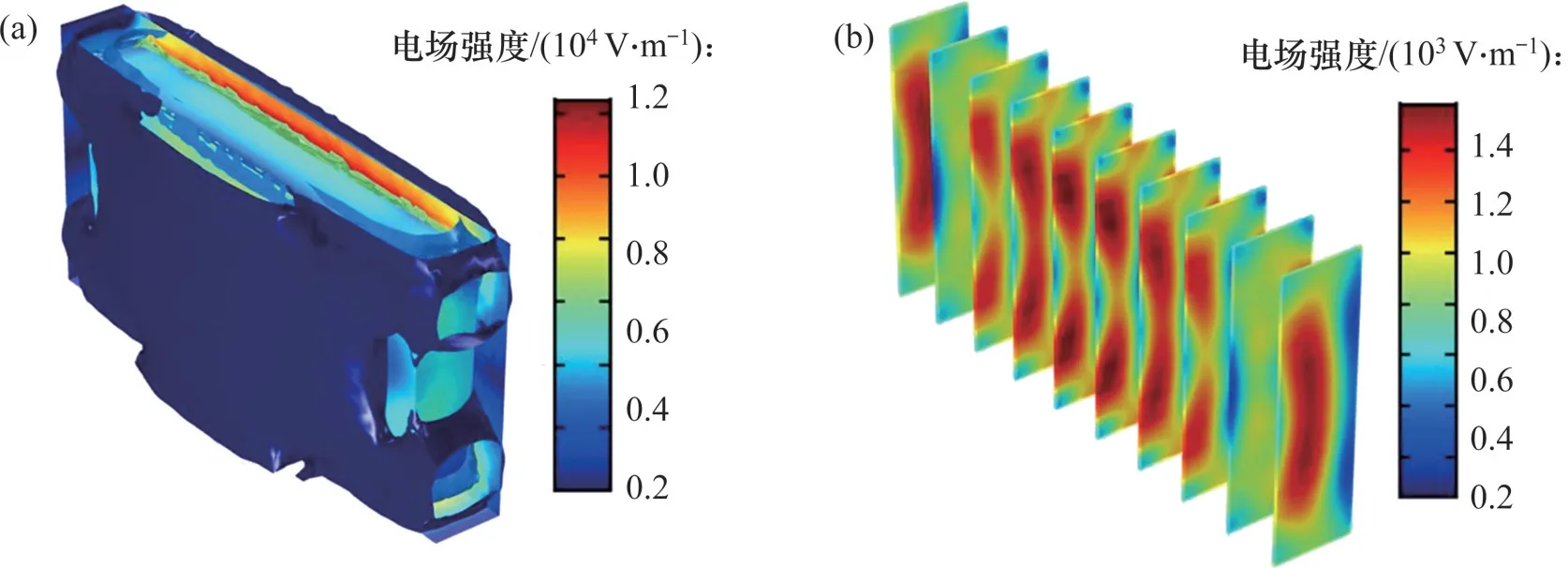
图8 含媒质二端口波导散射场分析Fig.8 Scattering field analysis of two port waveguide with medium

对上述对不同形状体积媒质进行散射分析，得到散射参数，并把求得的散射参数转换为阻抗参数，所得结果如表3所示。

表3 不同形状和体积的媒质S参数及等效阻抗ZTable 3 S-parameters and equivalent impedance Z of media with different shapes and volumes

以加热媒质为长方体1为例，馈入不同功率微波时，分别通过场路结合方法和有限元方法计算加热时媒质内平均电场强度，结果如图9所示。由图9可以看出：在馈入不同功率时，场路结合方法计算得到的媒质内的平均电场强度与有限元方法所得到的媒质内平均电场强度相对误差很小。

图9 加热时媒质内平均电场强度Fig.9 Average electric field strength in medium during heating

以加热媒质为长方体媒质1为例，在不同输入功率下，加热媒质10 s，分别通过场路结合方法和有限元方法计算媒质加热温度所用时间，结果如图10所示。由图10可以看出，计算微波加热相关问题时，场路结合方法耗时约为有限元方法的一半，体现了场路结合方法在计算速度上的优越性。

图10 2种方法耗用时间对比Fig.10 Comparison of time consumption between two methods

结合2.2节算法流程，通过计算媒质内的电场强度，可以计算出媒质加热的温度。

3.3 可行性验证

利用COMSOL Multiphysics多物理场耦合仿真实验环境，搭建相同的微波加热系统实验环境，对微波加热系统进行有限元分析。改变媒质体积、形状、输入功率和加热时间等实验变量，对比场路结合方法与传统的有限元方法在媒质加热效果方面的计算结果，结果如图11所示。

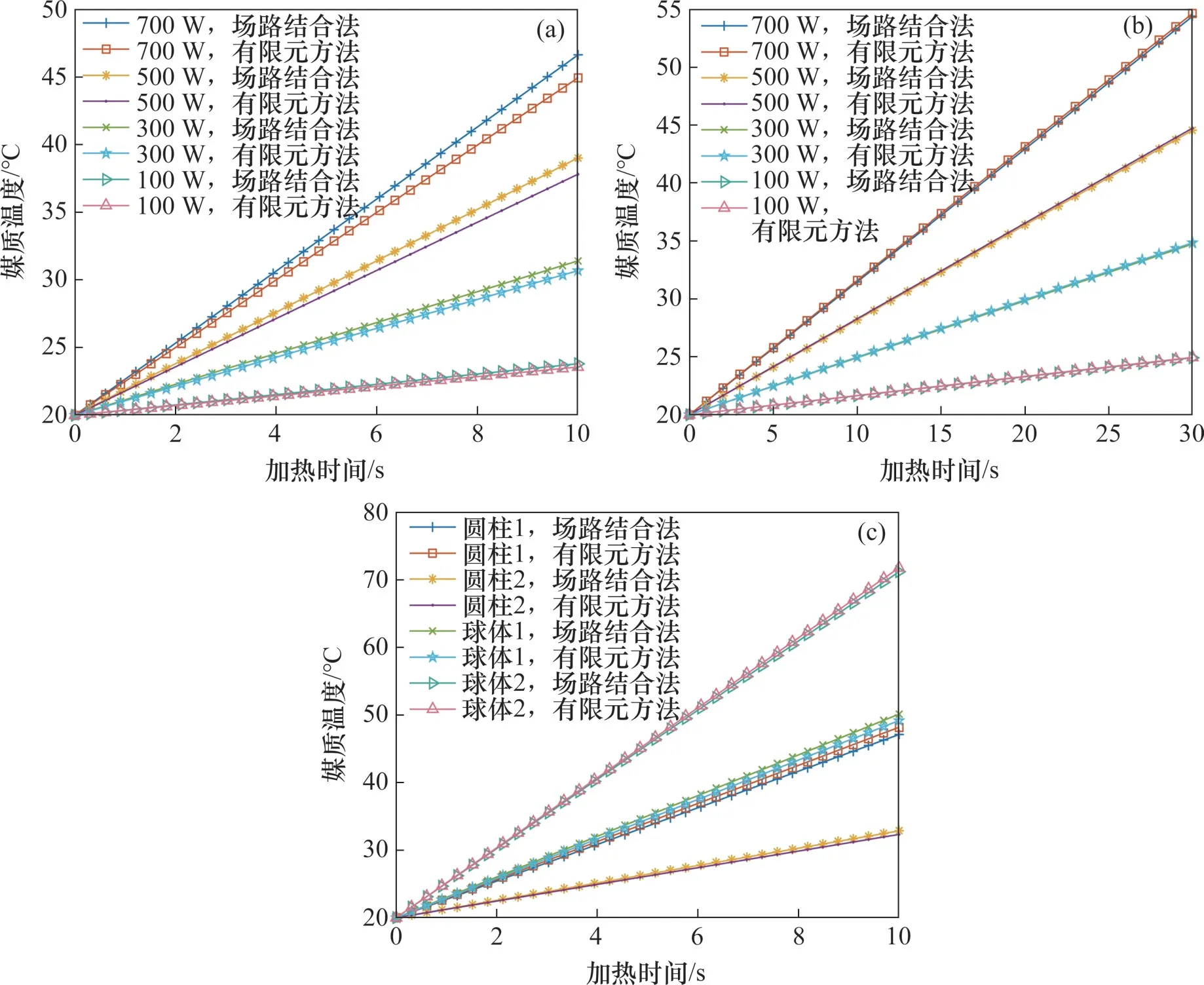
图11 不同媒质形状下加热温度计算结果对比Fig.11 Comparison of calculation results heating temperature for different shapes and volumes

1)改变输入功率，在700、500、300和100 W这4 种输入功率下，加热长方体1，时间为10 s。对比2种方法得到的媒质域的平均温度，其结果如图11(a)所示。

2)改变长方体媒质体积和加热时间，在700、500、300 和100 W 这4 种输入功率下，加热长方体2，时间为30 s。对比2 种方法得到的媒质域的平均温度，其结果如图11(b)所示。

3)改变媒质形状和体积，在1 000 W输入功率下，加热圆柱体1、圆柱体2、球体1和球体2，时间为10 s。对比2 种方法得到的媒质域的平均温度，其结果如图11(c)所示。

通过3组实验，分析不同条件下场路结合方法相对于有限元方法的计算相对误差δ可知，场路结合方法的计算误差在0.14%～3.77%之间，如表4所示。因此，场路结合方法能够有效求解不同条件下的微波加热问题。

表4 场路结合方法相对于有限元方法的加热温度相对误差δTable 4 Heating temperature relative error δof fieldroad combination method relative to finite element method

4 结论

1)提出一种结合全波场方法和等效电路方法的场路结合等效电路模型分析方法，求解电磁热多物理场耦合方程组，从而求得微波加热媒质过程中媒质的整体温度。

2)从微波网络理论出发，建立微波加热系统的等效电路模型，通过全波场方法分析微波应用器腔体中电磁散射场，获取加热媒质、腔壁、微波馈口对微波传输的阻抗特性。考虑了微波反射和吸收的问题，同时采用遗传算法提高了场路结合方法计算加热媒质内部电场幅值的准确度。

3)与传统有限元计算方法相比，场路结合方法求解微波加热媒质时的计算时间大幅减少，并保持了较高的准确率。2种计算方法求得的微波加热媒质结果的相对误差为0.14%～3.77%，验证了本文提出的场路结合方法的可行性和有效性。