IGWO-IP&O算法在光储MPPT控制系统中的应用

庞清乐，郑 杨，马兆兴，何辰斌

青岛理工大学 信息与控制工程学院，山东 青岛 266520

“双碳”目标下，清洁能源的有效利用与智能化是新型电力系统的发展目标[1]。光伏作为清洁能源发电的关键组成部分，在未来的电力市场发展中，光伏发电装机量将持续快速增加[2]。最大功率点追踪（maximum power point tracking，MPPT）技术作为提升光伏发电效率的有效措施，近年来已成为国内外学者研究光伏发电的热门领域。

常用的传统MPPT技术有扰动观察法[3]（perturbation and observation，P&O）和电导增量法[4]（incremental conductance，INC）。上述方法虽在光伏发电系统中有着广泛的应用，但在实际工作环境下，太阳能电池板会受到尘土、云朵、楼宇等外界因素的遮蔽，出现局部阴影的情况（partial shading condition，PSC），此时光伏电池功率输出曲线为多峰值，传统的MPPT技术及其改进型变步长算法易陷入局部极值。

为解决上述问题，国内外学者将元启发式算法与其他控制算法相结合应用于MPPT技术中，如文献[5-8]分别将粒子群优化算法、蝙蝠优化算法、灰狼优化算法、蝗虫优化算法与模糊控制法相结合，以使功率输出更加稳定，但模糊控制法的模糊规则设定依赖于人为经验，设计存在困难。文献[9]将布谷鸟优化算法、自适应果蝇优化算法、广义回归神经网络、蜻蜓优化算法四种算法相结合，有效提升了光伏发电系统应对外界环境变化的能力，但广义回归神经网络需要大量的训练样本，空间复杂程度高，且多优化算法的融合进一步加深了系统的复杂程度。文献[10-13]分别将花朵授粉优化算法、粒子群优化算法、树种优化算法与小步长P&O相结合，相比文献[5-8]降低了光伏发电系统的设计难度，且证实了元启发式算法与传统MPPT算法结合的可行性，但小步长P&O 适应性差，当外界环境变化不足以重启元启发式算法时，其固定步长的工作模式仍能引起系统工作反复跨域最大功率点的现象，进而导致输出功率出现振荡，且上述基于元启发式算法的MPPT 控制还存在陷入局部功率极值的可能，追踪功率速度慢，搜索过程的稳定性不高。

灰狼优化算法[13]（grey wolf optimization，GWO）因其原理简单、便于操作，核心参数便于调节的优良特性而被应用于光伏逆变器[14]、风力预测[15]、铁路物流[16]等不同工程领域实践中。然而与大多数群优化类算法一样，GWO的全局搜寻能力，收敛速度和精度有待提升。

为提升GWO 的性能，专家学者对GWO 进行了改进，文献[17]采用两个不同的模糊系统对GWO 进行优化，以迭代、多样性度量、误差度量作为输入，对GWO中的参数a和C进行动态调整，改进了算法的求解精度和收敛性。文献[18]为快速完成全局搜索，将参数a的数值变化通过正弦函数进行计算，并引入量子局部搜索，以提高GWO 的求解精度和稳定性。文献[19]在引入Kent映射的基础上，再将三角函数和贝塔分布分别用于调整参数a和更新种群位置中，以此来提升GWO 的性能。文献[20]为了有效提升GWO的综合性能提出将混沌Tent 映射、对立学习机制、余弦函数和精英个体高斯扰动机制引入GWO中。文献[21]引入二次函数和粒子群思想，分别用以调整参数a和更新狼群位置。上述改进方法中的参数a均采用了非线性收敛的控制策略，但全局搜索与局部寻优的迭代次数占比无法调整，难以适应不同工程问题的需要，此外，上述文献的全局搜索能力和收敛精度仍有较大的提升空间。

针对上述文献中MPPT 控制及GWO 所存在的问题，提出一种基于改进型灰狼优化算法（improved grey wolf optimization algorithm，IGWO）与改进型扰动观察法（improved perturbation and observation，IP&O）相结合的多峰值MPPT储能控制系统。IGWO采用可调节非线性收敛因子和改进型莱维飞行与增强型醉汉漫步结合的搜索策略，使其具有优越的全局搜索和局部寻优能力。IGWO完成前期全局最大功率点（maximum power point，MPP）寻优后，采用IP&O 完成后期精确追踪，IP&O 减轻系统运行负担的同时，还能提升系统对环境变化的适应性。所提出的基于IGWO-IP&O 的光伏MPPT 算法可使整个光伏发电系统具有高追踪精度和更快的追踪速度，能满足不同PSC 下负载的用电需求，储能蓄电池的加入能够解决光伏阵列发电不稳定而无法满足负载用电的问题。

1 局部遮阴下光伏特性输出特性曲线

当光伏阵列处于PSC时，光伏电池会出现局部MPP现象（不匹配现象），即串、并联后的光伏电池总输出功率低于各块光伏电池单独工作的输出功率总和。由于光伏阵列内部不匹配现象的产生会引起热斑效应的出现，光伏电池通常会处在发热的状况。为减少光伏电池发热带来的功率损耗，在实际使用时一般会将光伏电池组件反并联旁路二极管，旁路二极管会使被遮蔽的光伏电池不再工作，保护光伏组件不会因光伏电池过热而被损坏，但光伏电池组件又会因旁路二极管的存在而出现功率输出曲线的多峰现象。

不同情况下光伏阵列输出特性曲线如图1 所示。C1为非PSC下的光伏阵列输出特性曲线，C2为PSC下多峰值功率输出曲线所示。在C2这种情况下，传统的MPPT算法会陷入局部MPP。

图1 不同情况下光伏阵列输出特性曲线Fig.1 PV array output characteristics curve under different condi-tions

除此之外，光伏电池在制作过程中的误差会使其特性存在差异，使用过程中还会出现破损、老化等问题，这些均会增加MPP 追踪的难度，影响整个光伏发电系统的发电效率。

综上所述可知，为保证光伏发电系统的发电效能，MPPT算法应能解决不同情况下的光伏输出多峰问题，使得系统输出始终运行于全局MPP。

2 基于IGWO-IP&O的MPPT控制算法

2.1 灰狼优化算法

灰狼优化算法根据狼群的等级管理制度，将灰狼种群分为α、β、δ、ω四个等级，并通过模拟狼群的狩猎行为达到寻优的目的。其中α、β、δ为狼群的领导阶层，分别对应算法中的最优解、次优解与第三解，ω在狼群中等级最低，为待选解。灰狼优化算法分为以下三方面：

（1）包围猎物

式中，Lp为灰狼与狩猎目标的间距；Xp(i)为狩猎目标位置向量；X(i)为灰狼个体位置向量；M和N为系数向量；i为当前迭代次数。

N和M系数向量计算公式如下：

式中，a0为线性收敛因子，随迭代过程数值由2 递减至0；r1、r2为[0，1]中的随机数。

（2）捕食

狼群对狩猎目标进行包围之后，β与δ以α为主导，逐步缩小包围圈，完成捕食猎物的任务。上述捕猎行为的数学描述为：

式中，Dα、Dβ、Dδ分别为α、β、δ与当前灰狼个体的距离；Xα、Xβ、Xδ分别为α、β、δ的位置；X为当前灰狼个体位置；X1、X2、X3分别用于计算当前灰狼个体向α、β、δ前进的方向与步长。

当前迭代周期中，灰狼的终末位置为：

（3）搜索和攻击猎物

系数向量N决定了灰狼种群是搜寻猎物还是攻击猎物。当|N|大于1时，灰狼种群将开始搜寻猎物，即进入迭代前期的全局搜索阶段。当|N|小于1 时，灰狼种群对搜寻到的猎物进行围捕，即进入迭代后期的局部寻优阶段。

系数向量M与系数向量N不同，M的数值在迭代过程中随机变化，影响着灰狼与狩猎目标之间的距离，用以加强灰狼种群的全局搜索能力。

2.2 改进型灰狼优化算法

2.2.1 可调节非线性收敛因子

GWO中的线性收敛因子a0影响着系数向量N的大小，故a0的取值同样决定了GWO 中狼群的捕猎行为。a0＞1 时灰狼开始搜寻猎物；a0＜1 时，灰狼处于围捕猎物的状态。但线性收敛因子无法较好地平衡全局搜索与局部寻优之间的关系，所以在近几年的算法研究和工程应用中，专家学者通常选用非线性收敛因子改进灰狼优化算法。

文献[22]中提出一种基于正弦函数的收敛因子a1,即：

式中，ainitial为初始值，afinal为终值，ε为调节系数，imax为最大迭代次数。式（8）延缓了收敛因子变小的速率，使得算法的全局搜索能力得到提升，但算法在迭代后期收敛速度变慢。

文献[23]中提出一种基于指数函数的收敛因子a2,即：

式中，k为调节系数。式（9）中以e为底的指数函数增强了收敛因子衰减的速率，但全局搜寻阶段的过快结束易使全局搜寻范围不足，陷入局部最优。

为兼顾算法的全局搜寻能力和迭代后期的收敛速率，文献[24]提出一种基于cos 函数变化规律的收敛因子a3,即：

式（10）减慢了收敛因子前期变小的速度，提高了后期收敛的速度。但全局搜寻与局部开发的迭代次数占比无法调节，且公式较为复杂，采用a4可达到相同的非线性收敛效果，其式如下：

经简化后的式（10）减少了设计难度，但恒定的全局搜寻与局部开发迭代次数占比难以适应不同的优化问题。为此，提出一种可用于调节全局搜索与局部开发迭代次数占比的非线性收敛因子，即：

式中，μ为调整系数，用以调节全局搜索与局部开发的迭代次数占比，μ越小全局搜索的占比越大(μ＞0)；φ为补偿系数，当imax较大时其值接近于1(φ＞0)。

线性收敛因子与非线性收敛因子的比较如图2 所示。由图2可知，所提出的可调节非线性收敛因子能在迭代初期使得收敛因子递减缓慢，并可以利用较少的迭代次数完成全局搜寻，提高了全局搜索的效率；进入局部寻优阶段时，收敛因子递减速率加快，算法的收敛速度也随之提升；根据实际需要调节μ可获得不同的全局搜索与局部寻优迭代次数占比。

图2 线性收敛因子与非线性收敛因子的比较Fig.2 Comparison of linear convergence factor and nonlinear con-vergence factor

2.2.2 改进型莱维飞行和增强型醉汉漫步策略

GWO 的全局搜寻能力往往取决于狼群的领导阶层，由于GWO 最优保存策略的存在，在算法迭代的后期，狼群均会向领导阶层的狼移动，因此狼群中的领导阶层是解决GWO后期早熟收敛、无法跳出局部极值、收敛结果不佳等问题的关键。

受到布谷鸟优化算法[25]及鲸鱼优化算法[26]的启发，提出一种基于改进型莱维飞行与增强型醉汉漫步策略相结合的搜索方法。全局搜索阶段采用改进型莱维飞行，使灰狼可以充分搜索空间内所存在的猎物，增强GWO 全局寻优能力；局部寻优阶段采用增强型醉汉漫步策略，使灰狼能够围绕猎物快速收缩包围圈，保证局部寻优快速性的同时，提升收敛精度。为减少算法的计算时间，该搜索方法仅用于α狼。

传统莱维飞行的位置更新公式为：

式中，X(i)、X(i+1)为狼群解向量第i代和第i+1 代的迭代值；λ为步长缩放因子；参数β取值在[0，2]之间。levy(β)为遵循莱维飞行分布的步长函数，其数学描述如下：

式中，γ为飞行步长限定系数，xbest为当前最优解；U,V服从均匀分布，即U～N(0,δ2),V～N(0,1)。δ2取值方式如下：

β能快速调节莱维飞行的步长，莱维飞行搜索范围与其自身数值大小成负相关，在现有文献中常取3/2，但这一定值的选取容易造成莱维飞行在迭代前期步长受限，出现搜索距离过小的问题[27]。

为解决上述问题，提出一种基于双曲正切函数的动态参数调整策略，动态参数β计算方式如下：

式中，ε1、ε2为可调节因子，r3为[-1,1]的随机数。

动态参数β与参数β为定值时的随机步长取值比较如图3所示。β为定值3/2时，随机步长过小，易导致灰狼的运动较为集中，搜索范围不足。而动态参数β可令随机步长增大，使得系统能够充分进行全局搜索，并增强了莱维飞行跳出局部最优的能力。

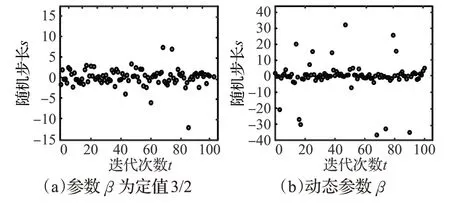
图3 动态参数β 与定值参数β 的比较Fig.3 Comparison of dynamic β parameters and constant β parameters

为提升GWO 局部寻优能力，将醉汉漫步[28]与气泡网狩猎策略[29]相结合，构成增强型醉汉漫步模型，该模型下的位置更新表达式为：

Xj、Xk为狼群解向量的第i代两随机迭代值；l为[-1,1]的随机数；b为对数螺旋函数的常量系数；Di为醉汉漫步步长函数，其表达式如下：

式中，r4为[0，1]的随机数；step为醉汉漫步步长，可设为定值或动态值；π 为圆周率。

对数螺旋三维曲线如图4 所示。该局部寻优搜索策略下，算法充分开发最优解范围内的空间，围绕最优解迅速收敛。最终通过贪婪算法比较原解与新解之间的适应度，淘汰适应度较差的解。上述两种策略采用概率选择方式进行转换。

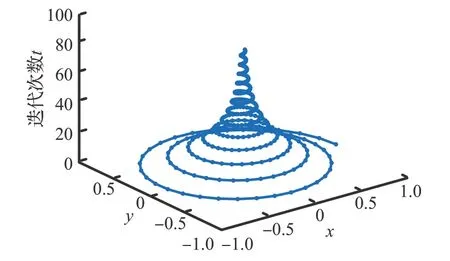
图4 对数螺旋三维曲线Fig.4 Logarithmic spiral 3D curves

2.2.3 基于步长欧氏距离的比例权重

为进一步增强算法求解多峰值寻优问题时的性能，IGWO算法采用文献[30]引入的基于步长欧氏距离的比例权重，如式（20）所示，此式可良好地避免全局搜索和局部寻优之间失衡问题的发生，并有效防止算法陷入局部最优的问题中，方便在实际工程中使用。

式中，W1、W2、W3分别为狼α、β、δ的权重参数。

2.3 IGWO具体流程

步骤1初始化系数向量N和M，最大迭代次数imax和狼群个体位置。

步骤2计算狼群个体适应度并排序，选出最优解、次优解与第三解，分别为狼α、β、δ。

步骤3根据式（12）计算非线性收敛因子a(i)，根据式（3）、式（4）更新系数向量N、M。

步骤4若rand＜0.5，狼α位置根据式（14）的改进型莱维飞行进行更新，此时莱维飞行中的β为动态参数；若rand＞0.5，狼α位置选用式（17）进行更新。

步骤5狼群中其余个体根据式（5）和式（6）更新位置。

步骤6通过贪婪算法比较原解与新解之间的适应度，淘汰适应度较差的解。

步骤7当达到设定的最大迭代次数imax时停止算法，根据式（20）输出最优解。

2.4 IGWO算法测试

为验证所提出算法的性能，采用8 个测试函数将IGWO与GWO、粒子群优化算法（PSO）、基于莱维飞行和随机游动策略的灰狼优化算法[30]（LRGWO）、基于维度学习的灰狼优化算法[31]（DLHGWO）、基于Chebyshev融合狼群协同围攻策略的改进灰狼优化算法[32]（CCAGWO）进行仿真实验比较。测试函数f1～f8的相关信息如表1所示，表中测试函数f1～f5为单模态函数，测试函数f6～f8为多模态函数，这两类测试函数的组合实验能全面地评估IGWO 全局寻优和局部搜索的性能。实验硬件设施为Intel®CoreTMi7-7700HQ处理器，16 GB运行内存，软件环境为Matlab2019b。实验时设置的所有算法种群数均为30，最大迭代次数为600。设置PSO算法的认知系数c1、c2分别为1.2和1.6，ωmin为0.2，ωmax为0.8。为避免实验结果的偶然性，每种算法各自运行30次。

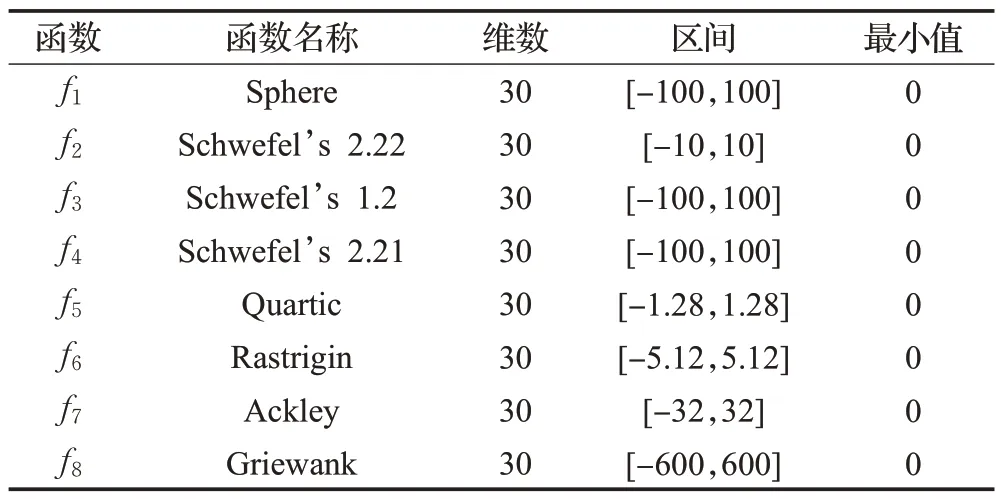
表1 测试函数Table 1 Test functions

六种算法在不同测试函数下的测试结果如表2 所示，对应的算法收敛对比曲线如图5 所示。表2 中的最优值与最差值体现算法的求解品质；平均值体现算法的求解准度；标准差反映算法求解时的鲁棒性。IGWO的数据加粗显示。根据表2 的实验数据和图5 的收敛曲线，具体分析如下：

表2 测试结果Table 2 Test results

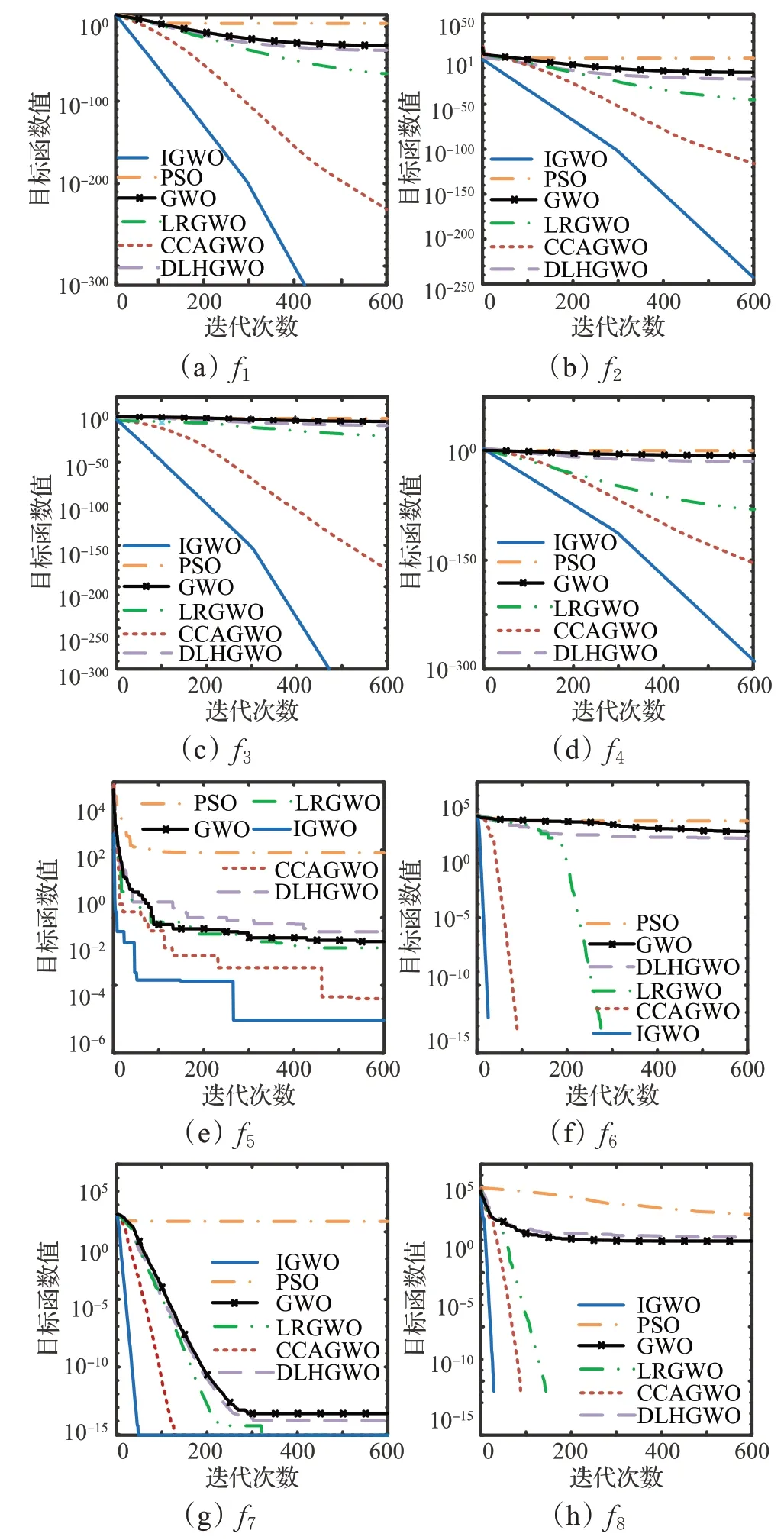
图5 不同测试函数时算法收敛对比曲线Fig.5 Comparison of algorithm convergence curves for different test functions

在8个测试函数之下，除PSO外，DLHGWO、LRGWO、CCAGWO和IGWO的求解精度均优于GWO，但DLHGWO求解精度的提升并不明显。IGWO在测试函数f1～f5下的最优值、最差值、平均值、标准差均小于其他五种算法，除函数f5外IGWO的标准差均达到了0值。在面对f6～f8这类多局部极小值函数时，IGWO的稳定程度和寻优精度依然可以得到保证。IGWO和CCAGWO均可准确稳定地找到测试函数f6和测试函数f8的最小值0，但IGWO收敛速度更快，在给定的600次迭代次数下，先于CCAGWO达到最小值0。在测试函数f7下，CCAGWO和IGWO均收敛于同一数值，收敛精度高于其他4种算法，但相比于其他测试函数下的收敛精度有显著的下降，对f7函数的寻优效果并不理想，LRGWO 的算法也出现了同样的情形，但IGWO算法依然发挥了其收敛速度快的优势。

综上所述，6种算法中性能最优的为IGWO。

2.5 改进型扰动观察法

P&O因结构简单、容易实现的优点，在光伏发电系统中得到普遍应用。但P&O的固定步长扰动机制使其无法兼顾追踪速度与收敛精度，为此提出一种变步长P&O，以变步长S替代P&O中的固定步长，步长S的计算公式如下：

式中，ΔUmax为步长最大值；ΔP为功率变化量；π 为圆周率；k为控制步长变化速率的调节参数。

变步长特性曲线如图6所示，k值越小步长变化越慢，k值越大步长变化越快。k值的设定可有效应对实际追踪中外界环境条件频繁变化所带来的步长不稳而引发的功率抖动问题。

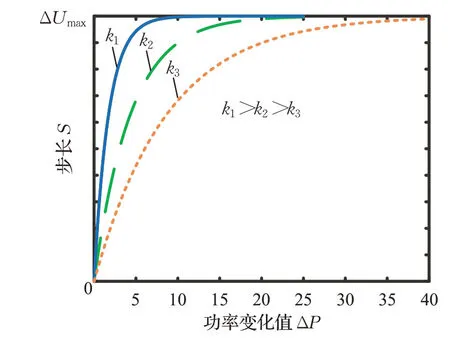
图6 S-ΔP 特性曲线Fig.6 S-ΔP characteristic curve

IP&O工作流程如图7所示。首先将测量到的相邻工作点电压，电流分别做差计算出dP与dU，通过dP和dU的变化是否同步来确定扰动的方向，即dP和dU的变化趋势一致则增加步长，以较大步长追踪MPP，反之则减小步长，直至工作点运行在MPP 处停止扰动。扰动步长值S随着工作点变化不断更新，在工作点接近或远离MPP 时能迅速调节步长大小，防止输出功率出现大幅度的抖动，该方法无须人为试凑扰动步长，为整个光伏发电系统快速准确地追踪到MPP提供了重要保障。

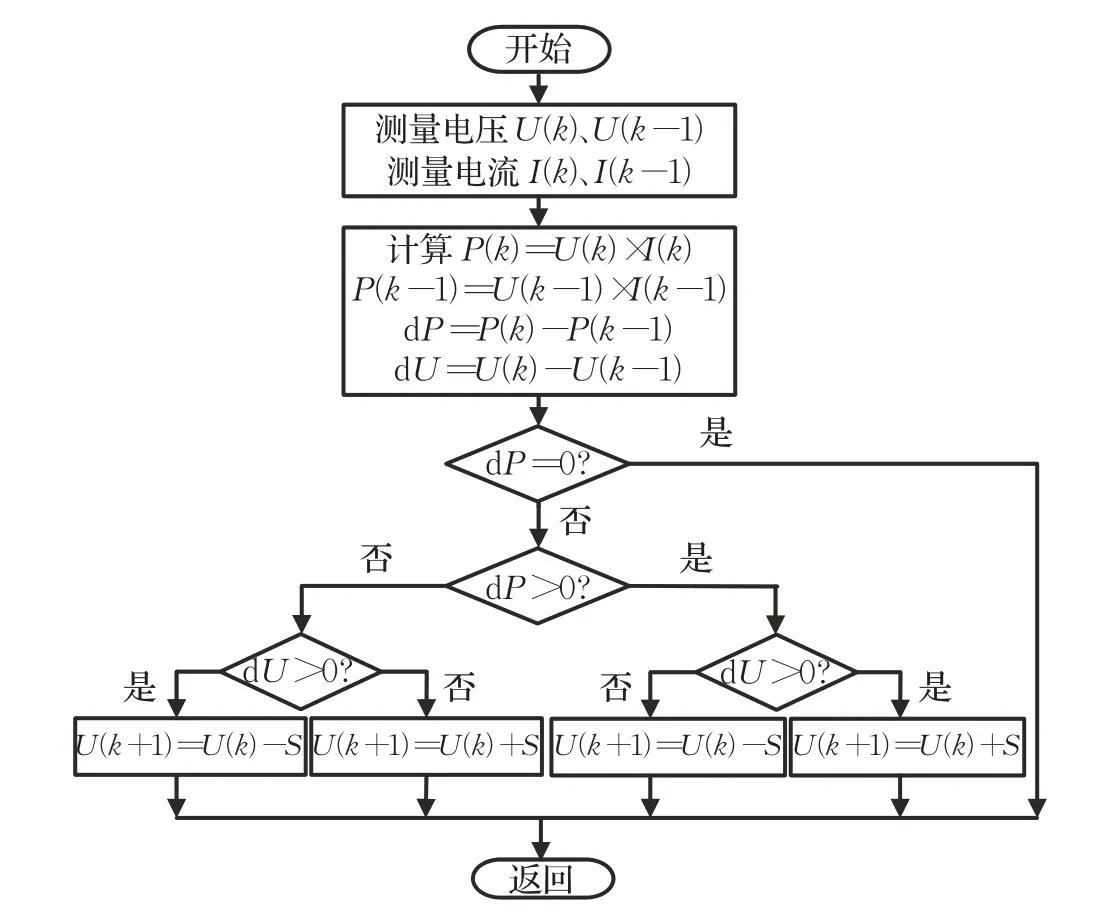
图7 IP&O工作流程图Fig.7 IP&O workflow chart

3 基于IGWO-IP&O的MPPT算法

在光储MPPT 控制系统中，所提出的MPPT 算法直接对占空比进行控制。IGWO 中，占空比为灰狼个体，狩猎目标为全局MPP。当局部阴影情况发生时，基于IGWO-IP&O的MPPT算法首先采用IGWO经参数初始化、功率计算比较、调整灰狼个体位置快速逼近至MPP附近，由于IGWO采用了适应性强的非线性收敛因子及新的搜索策略，使得算法全局搜寻的速度和精度均得以提升。但若系统始终处于IGWO 算法的运行状态会增加系统后期运行的负担，因此，在追踪后期采用IP&O，减少计算负担的同时，保证整个系统输出功率的稳定性，提高发电效率。

数次迭代之后灰狼种群位置趋于一致，此时输出功率差值逐步减小，系统工作点位于MPP 附近。为实现IGWO 与IP&O 的转换，IGWO 达到最大迭代次数便停止IGWO，此时系统进入IP&O寻优阶段。

随着外界环境的变化，如飘云、积尘、楼宇等因素引起的局部遮阴或光照强度发生变化时，光伏阵列的输出功率也会随之发生变化，此时需重启IGWO进行全局最大功率搜索，以降低功率损失。重启判别式[33]为：

式中，Pk、Pk-1为相邻时刻下的光伏输出功率，σ取值为0.05，判别式（22）一旦成立便立即重启IGWO算法。

上述IGWO-IP&O的算法流程如图8所示。

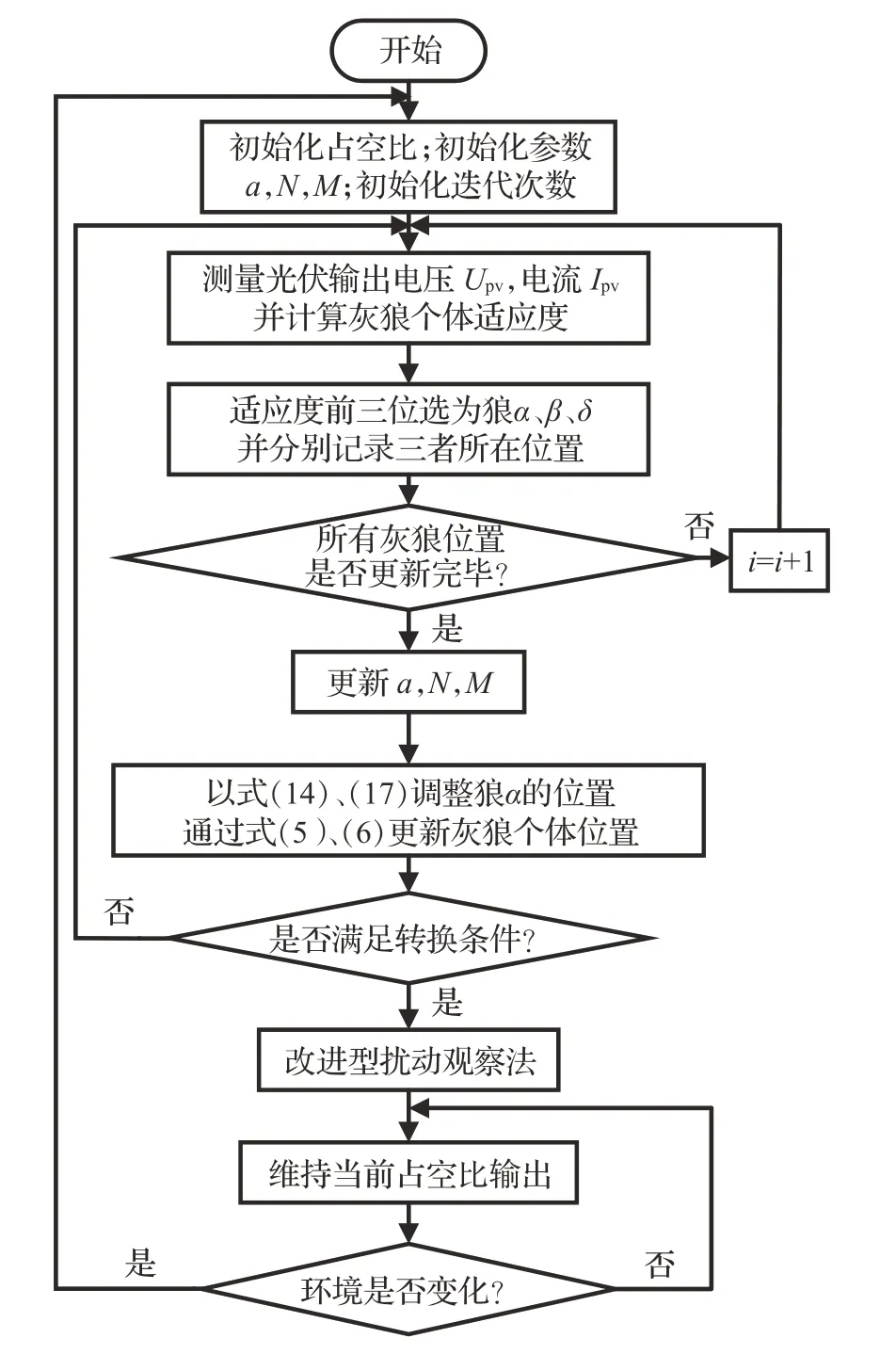
图8 IGWO-IP&O工作流程图Fig.8 IGWO-IP&O workflow chart

4 仿真分析

4.1 仿真模型

为验证基于IGWO-IP&O多峰值MPPT算法的有效性，采用5×1阵列的光伏MPPT储能控制系统进行仿真。

MPPT 储能控制系统模型如图9 所示，该模型主要由光伏阵列、Boost 电路、MPPT 控制器、PID 调节控制器、储能锂电池充放电控制模块五部分组成。其中，储能锂电池的充放电控制选用半桥式双向变换器，通过控制电感电流实现蓄电池与光伏电池间的能量交换[34]。光伏电池型号为1Soltech 1STH-215-P，Upv和Ipv分别为光伏电池的工作电压和电流，Uo为负载电压，VD为二极管。Boost 电路参数设置为：C1=5 μF、C2=20 μF、L1=8 mH、RL=15 Ω、IGBT 频率为5 kHz。储能锂电池参数设置为：C3=5 μF，电感L2=8 mH，额定电压220 V，电池容量500 Ah，初始荷电状态为50%。

图9 MPPT储能控制系统模型Fig.9 MPPT energy storage control system

4.2 静态遮阴条件下的功率追踪

为验证IGWO-IP&O算法在MPPT控制中的有效性，将GWO、花朵授粉优化算法（flower pollination algorithm，FPA）、改进型粒子群算法[35]（improved particle swarm optimization，IPSO）、基于莱维飞行的粒子群算法[36]（velocity of PSO based Levy flight，VPSO-LF）与它进行比较。

算法种群规模均设置为10。五块光伏电池板串并联数均为3×2，光照强度分别设置为1 000 W/m2、1 000 W/m2、800 W/m2、800 W/m2、400 W/m2以模拟静PSC下的三峰值P-U输出曲线，温度均设置为25 ℃，此时的理想最大功率输出为4 321 W。对比的指标为追踪时间、静态追踪效率ηstatic、动态追踪效率[37]ηdynamic。追踪时间为系统开始功率追踪到稳定输出时所需要的时间。ηstatic、ηdynamic计算式如式（23）、（24）所示：

式中，PPV(T)、PMPP(T)分别为T时刻下的光伏阵列实际输出功率值和理想输出功率值，MP为测试周期。

五种算法静态PSC 下的功率追踪仿真波形如图10所示，仿真结果如表3所示。由图10和表3可知：GWO用时1 s完成功率追踪，最终输出值为4 015 W，ηstatic为92.91%，ηdynamic为90.81%；FPA 用时0.86 s 完成功率追踪，最终输出值为4 306 W，ηstatic为99.60%，ηdynamic为94.88%。IPSO用时0.82 s完成功率追踪，最终输出值为4 319 W，ηstatic为99.95%，ηdynamic为95.17%；VPSO-LF用时0.79 s完成功率追踪，最终输出值为4 318 W，ηstatic为99.93%，ηdynamic为97.13%；IGWO-IP&O 用时0.05 s完成功率追踪，最终输出值为4 320 W，ηstatic为99.97%，ηdynamic为99.89%。

表3 静态PSC下仿真结果Table 3 Simulation results under static PSC

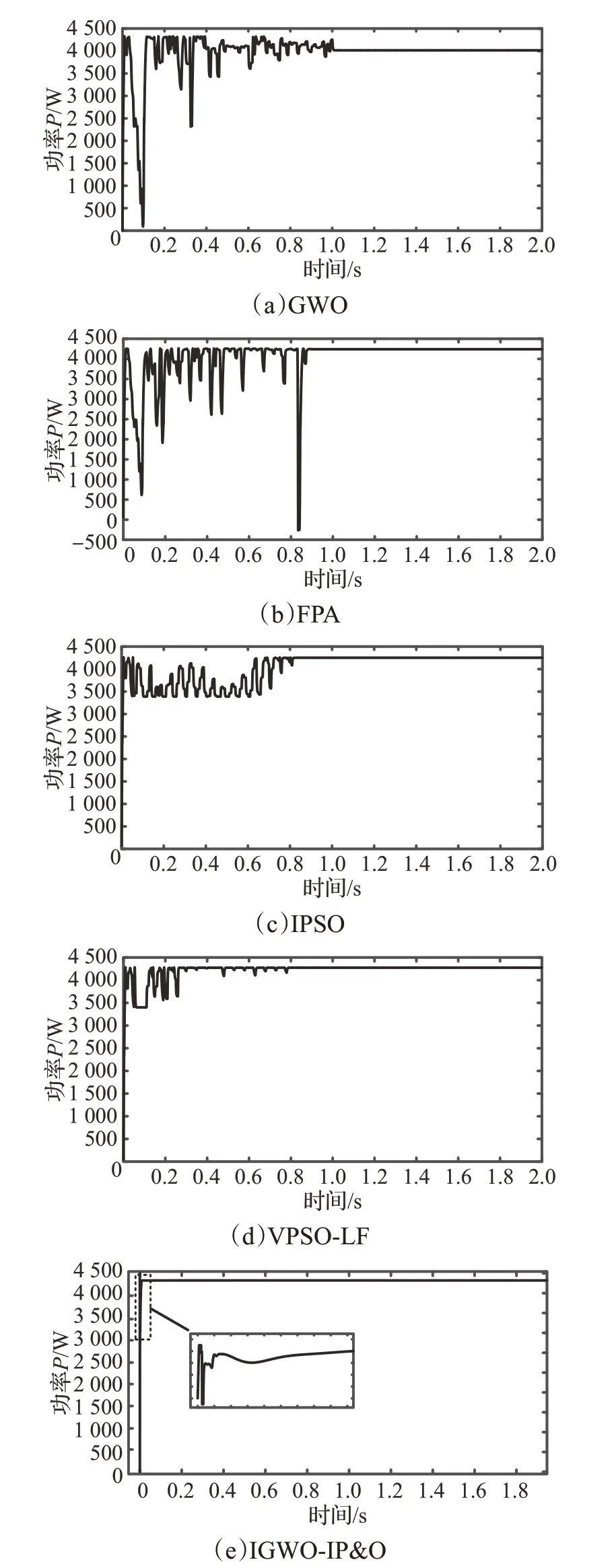
图10 静态遮阴条件下仿真对比图Fig.10 Simulation comparison diagram under static shading conditions

通过上述数据分析和仿真波形可知，在开始进行功率追踪的瞬间，五种MPPT 算法均响应迅速，除GWO外，静态追踪率均为99%以上，但IGWO-IP&O在功率追踪过程中未出现明显的功率波动，追踪时间短，输出功率的动、稳态精度均优于其他算法。

4.3 动态遮阴条件下的功率追踪

为进一步验证IGWO-IP&O 的优越性能，将五种算法在动态PSC下进行对比，并接入储能锂电池观察其在不同光照强度下的工作状态。

以4.2节静态PSC的三峰P-U曲线为模式1，四峰P-U曲线为模式2，五峰P-U 曲线为模式3，模式2 下五块光伏电池板光照强度分别设置为1 000 W/m2、1 000 W/m2、400 W/m2、800 W/m2、600 W/m2；模式3 下五块光伏电池板光照强度分别设置为1 000 W/m2、900 W/m2、300 W/m2、800 W/m2、700 W/m2，温度均为25 ℃。模式2与模式3理想输出功率分别为3 455 W 和3 921 W。模式1-模式2切换时间点为1.5 s处，模数2-模式3切换时间点为3 s处。

五种算法动态PSC 下的功率追踪仿真波形如图11所示，仿真结果如表4 所示。由图11 和表4 可知，在模式1 下，五种算法分别用时0.89 s、0.82 s、0.82 s、0.79 s、0.01 s 完成功率追踪，最终输出值分别为4 019.4 W、4 310 W、4 319 W、4 318 W、4 320 W，ηstatic分别为93.02%、99.74%、99.95%、99.93%、99.97%；ηdynamic分别为90.81%、93.70%、89.18%、97.13%、99.90%；

表4 动态PSC下仿真结果Table 4 Simulation results under dynamic PSC

图11 动态遮阴条件下仿真对比Fig.11 Simulation comparison diagram under dynamic shading conditions

在模式2 下五种算法分别用时1 s、0.83 s、0.35 s、0.34 s、0.01 s完成功率追踪，最终输出值分别为3 447 W、3 289 W、3 451 W、3 451 W、3 454 W，ηstatic分别为99.76%、95.19%、99.91%、99.91%、99.97%，ηdynamic分别为97.24%、92.54%、98.17%、99.09%、99.87%；在模式2 至模式3 的变换过程中，GWO和FPA算法失效，最终输出值分别为3 575 W和3 254 W，ηstatic分别为91.18%和82.99%，ηdynamic分别为91.17%和83.18%；IPSO 追踪时间为0.40 s，最终输出值为3 915 W，ηstatic和ηdynamic分别为99.85%和99.03%；VPSO-LF追踪时间为0.36 s，最终输出为3 918 W，ηstatic和ηdynamic分别为99.93%和98.72%；IGWO-IP&O追踪时间为0.08 s，最终输出为3 920 W，ηstatic和ηstatic分别为99.98%和99.90%。通过上述数据分析可知，GWO和FPA在功率搜索过程中输出振荡较大，动态追踪精度、速度不如NPSO 算法和VPSO-LF 算法。IGWO-IP&O追踪速度与追踪精度均优于其他四种算法，搜索过程中振荡小，响应速度快，验证了IGWO-IP&O在MPPT控制中的有效性和优越性能。

在动态PSC 下的储能锂电池充放电特性曲线如图12 所示，荷电状态（SOC）变化曲线如图13 所示。在0～1.5 s 模式1 时，储能锂电池处于充电状态，此时储能锂电池以恒流状态进行充电，蓄电池电压随之逐步上升，SOC 变化曲线直线斜率代表充电速度，光照强度越高充电速度越快；在1.5～3 s 模式2 时，光伏电池发电量不能满足负载用电需要，为维持负载端的正常用电，此时储能锂电池快速进入放电状态，电压开始逐步下降；在3～5 s模式3时，系统发电量满足负载用电需要，此时蓄电池再一次进入充电状态，光伏电池为下一次向负载临时供电做好准备，由于此模式下的发电量少于模式1，故蓄电池在吸收剩余能量时的充电电流和电压均有所降低。蓄电池的仿真结果进一步证明了IGWO-IP&O在光储系统中的实用性。IGWO-IP&O解决了文献[38]所提出的改进型P&O在PSC下光储系统无法有效追踪MPP的问题。

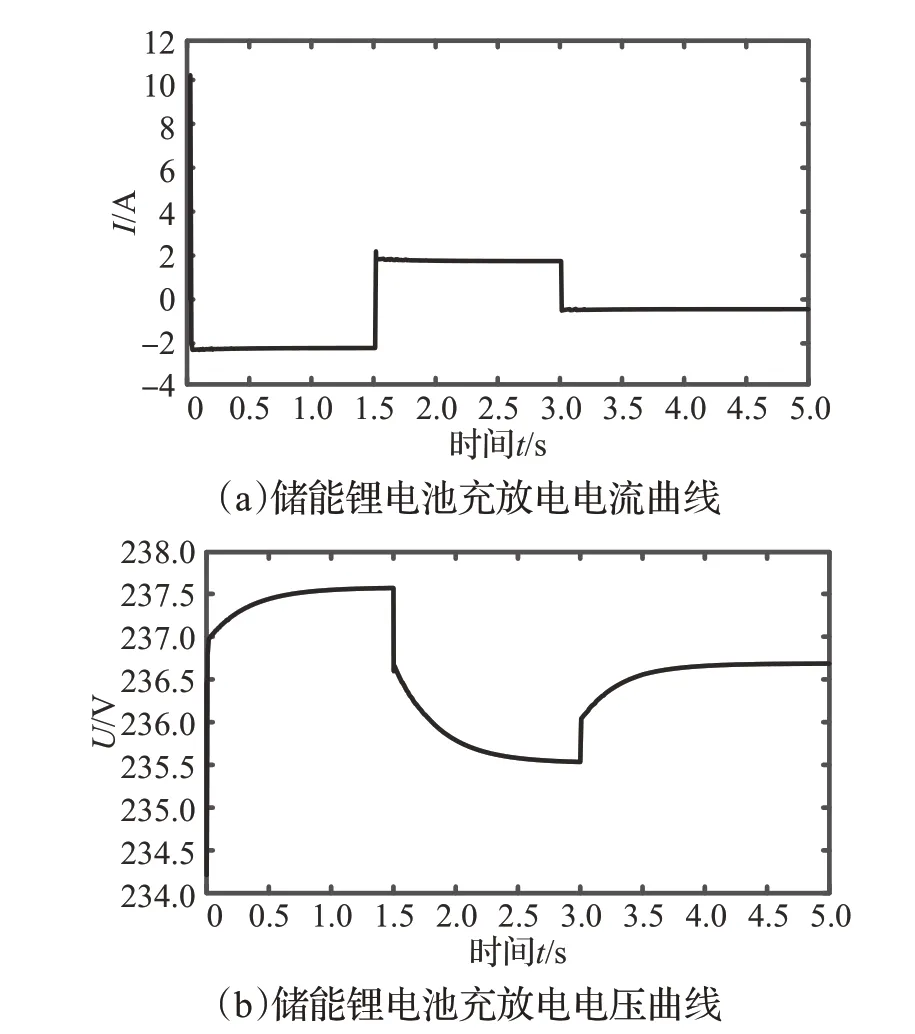
图12 储能锂电池充放电曲线Fig.12 Charge-discharge curve of lithium battery

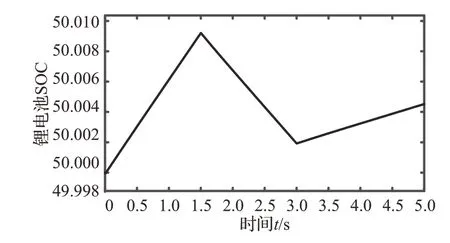
图13 储能锂电池荷电状态Fig.13 Charge state of lithium battery

5 结束语

针对局部遮阴情况下光伏发电系统难以有效追踪MPP的问题，提出了一种IGWO和IP&O相结合的光伏发电MPPT 控制算法。IGWO 采用可调节全局搜索与局部寻优迭代次数占比的非线性收敛因子，使算法适应性增强的同时，能够更好地平衡全局搜索与局部寻优之间的关系，此外，领导层狼α采用改进型莱维飞行与增强型醉汉漫步相结合的搜索策略，有效提升算法的全局搜索能力和寻优精度的同时，加快了算法收敛速度。通过与其他5个算法的比较实验，验证了IGWO的优越性能。最后将IGWO与所提出的IP&O算法结合应用于光伏发电储能系统中，仿真实验表明，基于IGWO-IP&O的光伏MPPT 控制追踪速度快，功率输出的动、稳态精度在不同的遮阴情况下均可达到99.9%，能够有效应对外界环境的变化，鲁棒性强。进一步的研究可对IGWO的种群初始化方式进行优化，使其可以更广泛地应用于其他电力工业领域之中。