贝叶斯优化的XGBoost信用风险评估模型

贾 颖，赵 峰，李 博，葛诗煜

山东工商学院 计算机科学与技术学院，山东 烟台 264005

信用贷款是借款人不需要提供抵押品或第三方担保，仅凭自己的信誉就能取得的贷款，并以借款人信用程度作为还款保证。信用贷款在国内蓬勃展开，银行和金融平台纷纷推出信贷产品抢占市场。然而借款人的违约行为会使银行和金融平台蒙受巨大的经济损失，影响其正常运行。信用风险评估可以帮助贷款审批决策者做出快速有效的判断，从而有效避免风险。信用评估本质上是一个二分类或多分类问题，可以使用统计方法或机器学习方法构建风险评估模型，根据贷款申请者提交申请表时填写的个人信息、银行记录的个人存贷款和历史信用信息、来自征信系统的信息等数据做出风险评估。

信用评估模型起步于统计计量方法[1]。统计方法有线性判别分析（LDA）和逻辑回归（logistic regression，LR）。LDA需要严格的假定条件，在实际应用中具有局限性。LR模型由于其稳健和可解释的优点曾被银行业广泛采纳。但LR的预测能力弱于后来出现的机器学习方法，因此，Bahnsen等人[2]提出了基于案例的代价敏感的LR模型用于信用评估。

机器学习方法出现后，神经网络（neural network，NN）、支持向量机（support vector machine，SVM）、决策树（decision tree，DT）等方法被用于信用风险评估。West[3]将5 种NN 模型应用到贷款信用评估中，结果表明三种NN 模型：混合专家模型（mixture-of-experts，MOE）、径向基函数（radial basis function，RBF）、多层感知机（multilayer perceptron，MPL）具有较高预测准确性。王静[4]提出一种基于Tanh 型粒子群的BP 神经网络和LDA 组合的信用评分模型，LDA用于特征提取，提取到的预测结果作为BP神经网络算法的输入变量，引入Tanh型函数粒子群优化BP 神经网络分类器的权值和阈，从而改善BP神经网络因收敛速度慢而导致的分类效果不佳的问题。Huang等人[5]建立遗传算法（genetic algorithm，GA）和SVM 结合的信用评估模型。该模型利用GA 进行特征选择并对SVM 高斯核函数的超参数进行优化，以相对较少的输入特征达到了较高的分类精度。虽然NN和SVM表现出了卓越的预测准确性，但其被称为“黑箱”算法，它们在结果的可解释性方面存在问题。事实上，监管机构通常要求银行给出拒绝信贷申请人的理由。NN和SVM不需要任何关于变量之间关系的信息，得出的结果也不容易被解释。银行也不能根据这些方法的结果给出拒绝贷款的理由。相对地，DT 由于其合理的解释能力而受到决策者的青睐[6]。Kao 等人[7]提出了一个基于分类回归树（CART）的贝叶斯隐变量模型，用于银行的信贷数据。与LDA、LR、NN、多元自适应回归样条曲线（MARS）和SVM 的性能相比，该模型的预测精度最高，而且Type-Ierror明显较低。

随着深度学习模型的出现，有相关文献将卷积神经网络（CNN）[8]、长短时记忆网络（LSTM）[9]用于信用评估。但CNN更适合于处理图像和文本数据这种天然地具有空间局部相关性的结构特征的对象，而用于信用评分的表格数据并不天然具有这样的特性。同样，信用评分也不是时间序列问题，而LSTM更擅长处理时间序列问题。

前面的研究都是针对单个复杂学习器在信用评估问题中的应用。然而来自不同银行的数据在数据规模、数据结构、特征类型和特征数量方面均存在差异，单个模型不能有效地解决所有问题[10]。集成学习模型可以集成多个弱学习器，形成一个强学习器。集成学习要求创建尽可能多的子模型，并且子模型之间必须有差异，因此集成学习具有较强的偏差-方差平衡能力。理论上即使每个弱学习器只有60%的准确率，集成500个这样的子模型，整体准确率可达到99.99%。经实践证明，集成学习模型确实比单个复杂分类器具有更优异的表现[11]，模型的泛化能力也显著提高。根据弱学习器集成方式的不同，集成学习分为两类：并行模式（如bagging、stacking）和顺序模式（如boosting）。并行模式中弱学习器之间是并列的关系，最后通过投票或求平均值得到结果；顺序模式中后面的弱学习器学习前面弱学习器的不足之处，最后累加得到结果。Dahiya等人[12]采用bagging方法集成同质分类器用于信用风险评估，采用投票方式决定最终分类结果。实验证明该模型能够在输入特征较少的情况下取得最好的表现，尤其使Type-Ⅱerror 明显降低。Xia 等人[13]提出采用堆叠（stacking）的方式集成异质学习器构成了一个三层的集成模型用于信用评估。由于每种基学习器都有自己固有的偏差，不同的基学习器可以弥补彼此的缺陷。实验证明该模型在准确率、AUC和Brier分数方面比单学习器（LR、SVM和DT）表现更好。Liu等人[14]提出了用多粒度扫描进行特征增强的多层梯度提升决策树（gradient boosting decision tree，GBDT）用于信用评分，该模型同时具有集成学习的鲁棒性和NN的表示学习能力，提高了信用预测的准确度。极端梯度提升树（XGBoost）是Chen 等人[15]在2016年提出的一种基于GBDT的改进，在GBDT的基础上做了如下提升：目标函数采用二阶泰勒展开，有利于梯度下降得更快更准；加入了正则化项，防止过拟合；加入了自动处理缺失值策略，对于特征的值有缺失的样本，XGBoost 可以自动学习出它的分裂方向；多线程并行计算特征切分点的信息增益，提高了运行效率。近年来，XGBoost在Kaggle等各类大数据竞赛中表现出卓越的性能。由于XGBoost的出色表现，该方法已被应用到疾病预测[16]、交通风险预测[17]、灾害预测[18]等领域，目前也有在金融信用风险评估的应用研究。Chang[19]提出了基于聚类的欠采样的XGBoost信用评分模型，在真实数据上测试，准确率和AUC优于LR、NN和SVM。Qin等人[20]将XGBoost用于信用风险评估，并采用适应性粒子群优化算法进行超参数优化，总体上超越了单分类器模型和其他集成学习模型。信用风险问题具有数据不均衡（违约样本大大少于未违约样本）、特征多、特征之间关系复杂、数据缺失多等特点。XGBoost非常适合于信用贷款的风险预测。首先，XGBoost采用树模型作为基分类器，天然地具有很好的可解释性。它能给出影响预测结果的特征重要性排名，也能显式地画出决策过程中的每棵决策树；其次，XGBoost允许使用AUC作为目标函数，同时具有提高少数样本权重的scale_pos_weight参数，对处理不均衡数据非常有效；第三，对于特征值有缺失的样本，XGBoost可以通过计算左右子树的增益来自动学习决策树的特征分裂方向，适合于处理贷款人信息缺失的数据。

尽管XGBoost表现出色，但由于XGBoost模型参数众多，只有经过精确的调参才能在特定领域有较好的表现[3]。常用的参数优化方法有人工手动调参、网格搜索（grid search，GS）、随机搜索（random search，RS）、遗传算法、粒子群优化（paticle swarm optimization，PSO）、贝叶斯优化等。人工调参工作量大，受主观经验影响大，对超参数数量多的情景不适用。GS和RS在评估一组新的参数时不能参考之前评估过的参数提供的信息，搜索速度慢，并且由于其搜索的不连续性，在非凸的目标函数上容易错过全局最优解。GA和PSO需要有足够多的试验样本点和目标函数评估，优化效率不高。贝叶斯优化算法是由美国UIUC 大学的Pelikan 等人[21-22]在2000年前后提出的。贝叶斯优化属于分布估算算法，是在GA 的基础上发展起来的，将概率模型引入了算法，来描述可行解的分布，并依此来指导种群进化。贝叶斯优化利用贝叶斯网络来建立解空间的概率模型，能显式地反映优化问题中各变量间的相互关系，更加符合问题的实质[23]。在解空间中采样新个体时充分利用了先验知识，对过去的经验进行总结，从而有方向性地提出更好的选择方案，收敛速度快，针对非凸问题依然稳健。

基于以上原因，本文提出了使用贝叶斯高斯过程（Bayesian Gaussian processes，GP）对XGBoost 模型进行参数优化的XGBoost-GP 模型，应用于信用风险评估中。

研究的创新点主要表现在：

（1）提出了使用贝叶斯高斯过程对XGBoost模型进行参数优化的XGBoost-GP 模型，应用于信用贷款违约风险预测中，与其他对照模型相比，预测准确率高，模型可解释性好。

（2）将贝叶斯高斯过程应用于XGBoost 的参数调优。贝叶斯高斯过程利用已知的参数点逼近目标函数。在搜索新一组参数时会在已知参数点的附近寻找均值和方差均较大的点，并使用采集函数平衡均值和方差的关系，针对非凸问题依然稳健，并且耗时少。

（3）利用国内人人贷平台采集的真实数据，数据不平衡度和缺失度较高，更能验证模型的预测能力和鲁棒性，同时更适合中国国情。

1 XGBoost算法原理及模型优化算法

1.1 梯度提升决策树

梯度提升决策树GBDT（gradient booting decision Tree）是基于树的梯度提升算法。每训练一个决策树模型（基分类器），都是去学习上一轮模型产生的错误（残差），它利用损失函数的负梯度作为上一轮基分类器犯错的衡量指标，在下一轮学习中通过拟合残差负梯度来纠正上一轮犯的错误。

GBDT 采用前向分步算法。首先确定初始决策树f0(X)=0，则第m步的模型是：

其中，fm-1(x)为当前决策树模型，通过最小化损失函数确定下一棵决策树T的参数Θm：

不断重复这个过程直到损失函数的值减小到一个限定的范围内。测试样本的最终值是所有决策树（基分类器）叶子节点值之和，即GBDT 将所有决策树的结论累加起来作为最终结论。针对不同问题的梯度提升树，使用的损失函数L不同，回归问题采用均方误差损失函数，分类问题采用指数函数。

1.2 XGBoost

XGBoost 是GBDT 的一种高效实现[24]，由华盛顿大学的陈天奇于2016年提出，并在文献[15]中证明了其计算复杂度低、运行速度快、准确度高等特点。XGBoost适当改进了GBDT，在损失函数上添加了正则化项，限制了每棵树的节点个数和叶子节点上的分数，相当于对树进行了剪枝和防止过拟合。

XGBoost的目标函数如公式（3）所示：

对于目标函数的优化，GBDT 采用的是梯度下降法，而XGBoost采用了在ft(xi)处进行二阶泰勒展开：

对于给定的树结构q，定义Ij={i|q(xi)=j}为所有被映射到第j个叶子节点的样本i的集合，该叶子节点的输出为ωj，则公式（5）可表示为：

那么目标函数objt的最小值可以用简单的一元二次方程的最小值求出，是每个叶子节点上的最优叶子权重。

目标函数取最小值：

其中，gi和hi因损失函数不同而不同，XGBoost支持自定义损失函数，只要该损失函数可以求一阶和二阶导数即可。

1.3 贝叶斯优化算法

超参数调整是机器学习中最重要的概念之一。超参数的设置是在模型训练之前解决的。机器学习算法令人满意的性能取决于有适当的超参数设置。XGBoost有大量超参数（包括继承自GBDT的超参数和它自己独有的超参数），这些超参数直接影响到模型的结构和模型的性能。因此，对超参数进行适当的调整就显得尤为重要。XGBoost的主要超参数如表1所示。

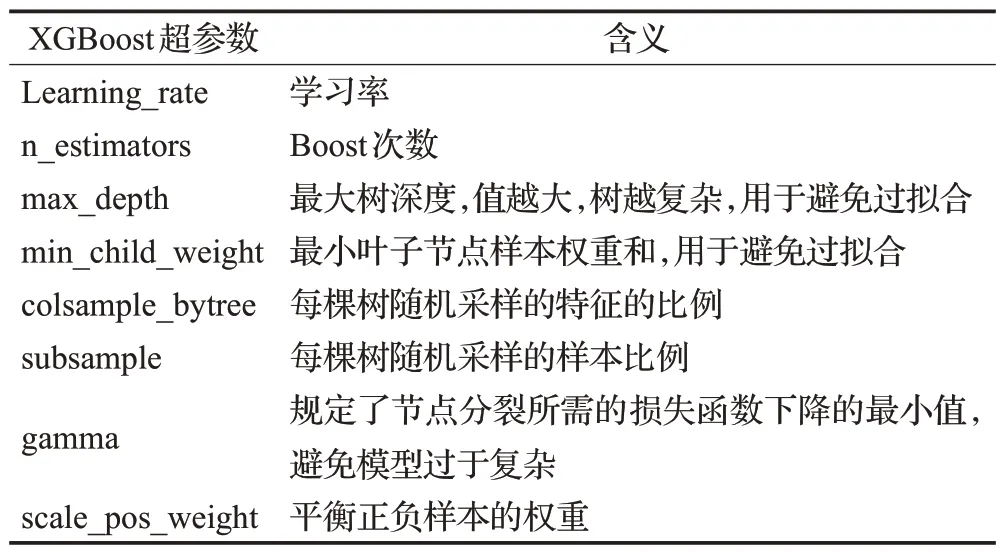
表1 XGBoost主要的超参数Table 1 Formulation of hyper-parameters of XGBoost

虽然GS 和RS 已经被广泛应用于机器学习模型的超参数优化，但由于XGBoost 中包含大量的超参数，每一次函数评估的计算成本非常高，这两种优化算法对XGBoost 来说是效率不高。贝叶斯优化提供了一种更优雅的调参方法[25]。贝叶斯优化假设超参数与需要优化的损失函数之间存在函数关系，而这个函数关系是一个“黑盒函数”，不能通过梯度下降法来获得最优解，但是可以通过一些先验的样本点逼近未知目标函数的后验分布[26]。通过对目标函数形状的学习，找到使结果向全局最优解提升的一组超参数。贝叶斯优化是一种近似逼近的方法，用各种代理函数来拟合超参数与模型评价之间的关系，然后选择最有希望的超参数组合进行迭代，最后得出效果最好的超参数组合。

由于高斯过程具有高度灵活又易于操作的特点，贝叶斯优化采用高斯过程去训练数据并学习目标函数的后验分布。高斯过程并不会得到每组超参数所对应的具体目标函数值，只会给出目标函数的概率分布，得到超参数在某个区域上目标函数的期望均值和方差。期望均值越大，表明目标函数效果越好。方差表示不确定性，方差越大，表明目标函数在该点更有可能获得最大值，非常值得探索。通常情况下，选择具有最大期望收益或不确定性的点来进行下一次的采样。在均值大的点处进行采样称为开发，在方差大的点处进行采样称为探索。采集函数是用来平衡开发和探索的函数，决定了下一个采样点的位置。随着采样点积累，目标函数的后验分布持续更新。在新的后验分布的基础上，使采集函数最大化的新的采样点不断被找到并加入到样本集中。一直重复这个过程直到达到最大循环次数或者目标函数值与最优解之间的差值小于阈值为止。

贝叶斯优化的伪代码如下。f(x)是模型的损失函数，D记录了超参数组合x和相应的损失函数值f(x)的组合。采集函数u决定了下一个采集的样本点xt的位置。

算法贝叶斯优化

1.3.1 高斯过程

高斯过程假设所有超参数符合多元高斯分布。高斯过程可以均值函数m:x→R 和方差函数k:x×x→R来定义，形式如下：

计算目标函数的后验分布的过程如下：

（1）t个样本构成了训练集D1:t={xn,fn}tn=1,fn=f(xn),假设函数f的值符合多元高斯分布f～N(0,K)。其中：

（2）基于函数f，计算新的采样点xt+1对应的函数值ft+1=f(xt+1)，根据高斯分布的假设，f1:t加上ft+1应该符合t+1 维高斯分布：

可以看出，高斯过程并不会返回ft+1的确切值，而只是给出其所有可能值的概率分布。如果采集的样本点足够多，高斯过程可以获得目标函数f(x)的近似估计。

1.3.2 采集函数

获取目标函数的后验分布之后，贝叶斯优化通过最大化采集函数u来获取目标函数f(x)的最优解。文献[27]指出，预期改进（expected improvement，EI）因为容易获得全局最优解并且操作简单，通常被选作采集函数。EI函数在探索当前最优解的周围区域时会计算参数点对目标函数改进所能达到的期望值。如果在算法执行后对目标函数的改进I小于期望值，那么当前最优解很有可能是局部最优解，算法会在其他区域寻找最优解。对目标函数的改进程度I是指新的采样点对应的目标函数值与当前最优值的差值：

根据EI函数的优化策略，试图最大化关于当前最优解f(x+)的EI：

当ft+1(x)-f(x+)≥0,ft+1(x)的分布符合均值为μ(x)，标准差为σ2(x)的正态分布。因此，随机变量I的分布是均值为μ(x)-f(x+)，标准差为σ2(x)的正态分布。I的概率密度函数为：

I的预期改进EI的定义如下：

综上所述，贝叶斯高斯过程调参具有迭代次数少，收敛速度快，计算成本低，对非凸问题依然稳健的特点，适合为XGBoost模型做超参数优化。

2 XGBoost-GP信用风险评估模型

基于贝叶斯优化后的XGBoost 信用风险评估模型的流程如图1所示。

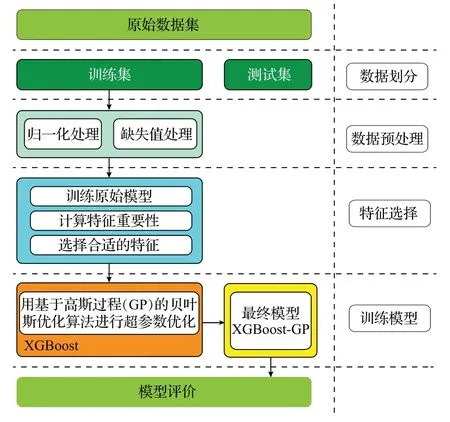
图1 XGBoost-GP信用贷款风险评估模型流程图Fig.1 Process of XGBoost-GP credit loan default risks

首先对客户个人信息和信用历史信息进行清洗，去掉无效数据，进行缺失值处理。基于数据集对XGBoost进行训练，分别采用GS、RS、贝叶斯高斯过程进行XGBoost的超参数调优，将训练好的XGBoost模型用于客户违约行为预测，并将模型与其他模型从评价指标和统计方法两个角度进行对比和评价。其中XGBoost-GP的结构如图2所示。

图2 XGBoost-GP结构Fig.2 Structure of XGBoost-GP

2.1 数据预处理

对数据进行0-1标准化和特征缺失值处理。虽然树模型几乎不受特征量纲的影响，但数据标准化可以大大提高模型的分类准确率。对比模型中的LR 和SVM 都是基于距离计算的模型，必须建立在特征量纲一致的基础上。因此，为了更好地进行模型对比，先对数据集的特征进行0-1标准化。训练数据表示为D={X,y}，其中X={x1,x2,…,xm}表示m维的特征空间，y={0,1}表示目标值，y=0 表示好样本（未违约样本），y=1 表示坏样本（违约样本）。对于样本的每个特征x，采用公式（22）进行0-1标准化。

为避免缺失值对实证分析的影响，对数据集进行缺失值处理。XGBoost有自己专门的缺失值处理策略，比传统的缺失值处理方法更适合树模型。对于没有缺失值处理策略的对比模型，事先对缺失值做如下处理：对于类别数据，采用众数来补全，对于数值型数据，采用平均值来补全。

2.2 特征选择

包括XGBoost 在内的基于树模型的集成学习模型都有特征重要性分数（feature_importances_属性）。先运行采用默认超参数的XGBoost 模型来计算特征重要性分数，然后按照特征重要性分数从高到低依次加入到调参后的预测模型中去，直到模型的预测准确率不再增加为止，然后去掉还没有加入到模型中的特征。对于对比模型中没有特征重要性属性的模型，先计算特征的F分数，然后再按照F 分数从高到低依次加入模型的方法，直到模型的预测准确率不再增加为止，然后去掉还没有加入到模型中的特征。

2.3 模型训练

为了避免数据集随机划分带来的偶然性，模型训练过程采用交叉验证。经过多次实验，最后决定采用5折交叉验证来进行数据集的划分。

3 实验设置

本实验的目的是构建贝叶斯超参数优化后的XGBoost模型，并与其他单个模型以及集成学习模型在信用贷款风险评估中的效果进行对比。

3.1 数据集

为了验证XGBoost-GP 模型的性能，使用了3 个数据集进行验证。其中German和Australia信用数据来自UCI机器学习数据集（http：//archive.ics.uci.edu/ml/datasets.php），P2P-ren 是通过爬取人人贷平台数据所得。三个数据集的结构如表2所示。

表2 数据集格式Table 2 Formulation of credit data

3.2 对比模型

为了验证XGBoost-GP模型在信用风险评估中的效果，采用了9种在信用贷款评估领域使用较广并效果较好的模型与XGBoost 模型进行比较。包括单学习器模型（LR、DT、BP-MPL、SVM）和集成学习模型（Bagging-DT、RF、AdaBoost-DT、GBDT）。

LR，是一种二分类模型，常被用作信用评估的基准模型[9]。LR 根据样本的特征推测样本属于某一类别的概率，然后根据概率进行二分类。在信用贷款问题中，假设借款人违约的概率为P，则未发生违约的概率为1-P,P∈[0,1]。则LR公式可以表示如下：

其中，β0是常数系数，βi是样本特征xi对应的系数。

SVM[28]，是另一种适合于信用评估的二分类模型。依据结构风险最小化原则，SVM 在样本空间里找到一个最优分类超平面，将样本划分为两个类别。SVM 依赖核函数将线性不可分的样本映射到高维空间中变成线性可分。常用的核函数有线性核函数、多项式核、径向基核（RBF）等。SVM 尝试找到最优的决策边界，使得在超平面两边最近的点与超平面的距离之和越大越好。

BP-MPL，是一种按照误差逆向传播算法训练的多层前馈神经网络（MPL）。BP神经网络结构特点为多层全连接与误差反向传播。可以用于分类和回归问题。

DT，广泛应用于信用评估。一棵决策树包含一个根节点、若干个内部节点和若干个叶子节点；每一个内部节点代表基于一个属性的决策，内部节点下的每个分支代表决策后的输出，叶节点对应于最终决策结果。根据选择分支属性的依据不同，决策树分为CART（根据Gini系数）和C4.5（根据信息增益率）。

集成学习模型包括：

（1）并行模型模式

Bagging[29]，从训练集X中随机可放回抽样取n个样本，产生子训练样本，并在子训练集上构建基分类器；重复抽取k次得到k个基分类器；票选基分类器结果中最多的类作为Bagging 模型的输出；基分类器可以是ID3、C4.5、CART、SVM、Logistic回归等。

RF[30]，从样本集中有放回地采样选出n个样本；从所有特征中随机选择k个特征，然后选择最佳分割特征将决策树划分为左右子树，建立CART 决策树；重复以上两步m次，即建立了m棵CART决策树；这m个CART树形成了随机森林，通过投票表决结果，决定样本属于哪一类别。

（2）顺序模式

Adaboost[31]，先给样本赋予相等的权值，然后引入分类算法构建分类模型；提高被错误判断的样本的权值，降低被正确判断的样本的权值，重新构建分类器。重复这个过程，得到基分类器，对基分类器的预测效果进行排序，效果好的得到更高权值。加权投票得到最终的分类结果。

GBDT，将负梯度作为上一轮基分类器犯错的衡量指标，在下一轮学习中通过拟合负梯度来纠正上一轮犯的错误。GBDT是基于树模型的梯度提升。

为了验证贝叶斯优化对XGBoost预测效果的提升，实验同时对比了使用GS和RS进行参数优化后的XGBoost模型：XGBoost-GS和XGBoost-RS。各种优化算法的超参数搜索空间如表3所示。

表3 XGBoost超参数优化搜索空间Table 3 Search space set and number of computations of each hyper-parameter optimization method

每个对比模型通过GS和5折交叉验证寻找使得模型F1分数最高的超参数作为最优超参数。

3.3 评价指标

采用预测准确率、Type-Ierror、Type-Ⅱerror、精准率、召回率、F1分数作为评价指标。以上指标都是基于表4所示的混淆矩阵。

表4 混淆矩阵Table 4 Confusion matrix

准确率（Accuracy，ACC），预测正确的样本占总体样本的比例。

Type-Ierror，所有违约样本中被误判为未违约的比率。

Type-Ⅱerror：所有未违约样本中被误判为违约的比率。

因为如果违约的样本被预测为未违约，造成的金融风险更大，是信用评估中要重点避免的问题，所以模型要重点降低Type-Ierror指标值。

精准率（Precision），准确预测为违约样本数占所有预测为违约的样本数的比例。

召回率（Recall），准确预测为违约样本数占所有违约样本数的比例。

F1 分数（F1-score），综合考虑了精准率和召回率的平衡。它是精确率和召回率的调和平均数，最大为1，最小为0。

4 实验结果分析

本实验将5 折交叉验证平均结果作为最终结果。实验环境是为Sklearn和python3.8以及基于高斯过程代理的sklearn贝叶斯优化包bayes_opt。

4.1 模型评价结果

ACC 是最主流和直观的评价指标之一，代表了模型准确度的整体水平。但在信贷风险评价领域，对于违约行为预测的准确度直接影响了金融机构的经营风险和收益，Type-Ierror体现了对违约行为预测的错误率，所以较低的Type-Ierror 是好模型的重要衡量标准。F1-score综合了对违约行为预测的精准率和召回率两个指标，所以将F1-score 作为衡量模型好坏的重要的指标。表5～表7 显示了XGBoost 和对比模型在三个数据集上的表现，其中表现最好的用黑体标出。

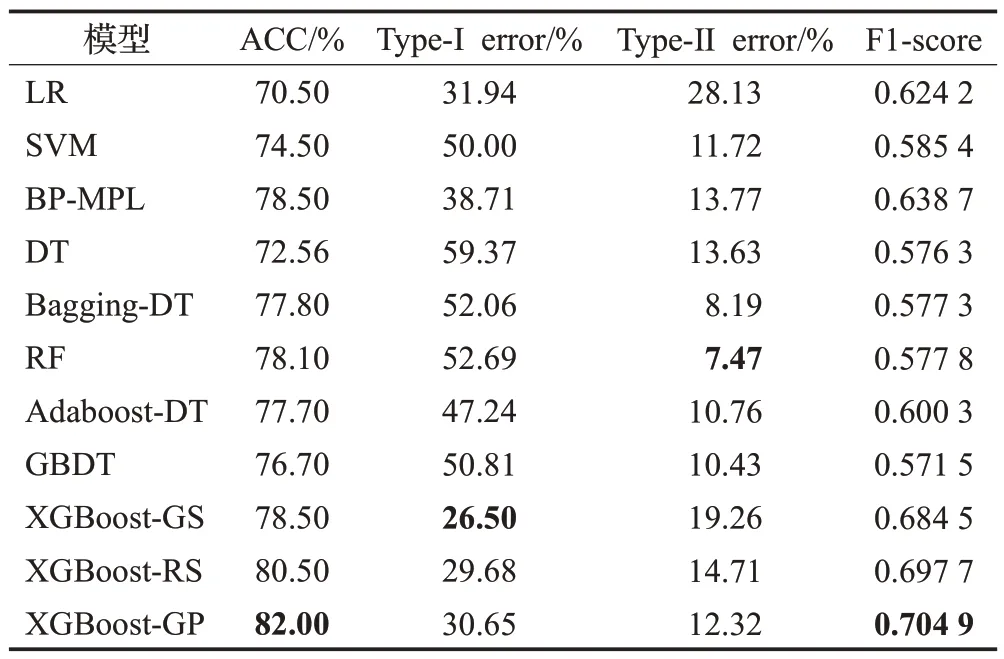
表5 在German数据集上模型准确性评估结果Table 5 Result of performances on German dataset on performance measures

在German 数据集上（见表5），XGBoost-GP 获得了最好的预测准确率ACC（82%）和F1-score（0.704 9）。其ACC相比表现最好的单分类器BP-MPL高出3.5个百分点，比表现最好的集成分类器RF高出3.9个百分点。三个XGBoost 模型的ACC 和Type-Ierror 在所有模型里表现最好，说明XGBoost模型对整体样本的预测准确率和对少数样本（这里是违约样本）的预测准确率都很好，在处理非均衡数据时具有优势，对非均衡数据中的少数样本的预测能力很强。这种对少数样本预测能力的提升归功于XGBoost超参数中scale_pos_weight对样本权重的平衡能力。RF在Type-Ⅱerror指标上表现最好，说明RF 倾向于将样本判断为好样本。在所有对比模型中，BP-MPL 在ACC 和F1-score 指标上表现最好，在Type-Ierror 指标上仅次于LR，说明在信用评估领域，BP-MPL可以作为一个备选模型。

Australian 是一个相对均衡的数据集，违约样本数量略多于未违约样本，因此Australian数据集上（见表6）各个模型的表现都高于German 数据集，且正负样本的预测错误率也相对均衡。XGBoost-GP 模型在除了Type-Ⅱerror 之外的所有指标上都取得了最好的表现。ACC相比表现最好的单分类器LR高出3.77个百分点，比表现最好的集成分类器RF高出3.62个百分点。SVM的Type-Ⅱerror值在所有模型中最低，而Type-Ierror值最高，说明SVM倾向于将样本判断为好样本，对违约行为的预测能力较差。F1-score体现了模型对正负样本错分代价的综合评判指标，XGBoost-GP 在该指标上表现最好（0.912 4），比表现最好的对比模型RF高出0.042 1。在所有对比模型中，RF 在ACC 和F1-score 指标上表现最好，可以作为一个备选模型。

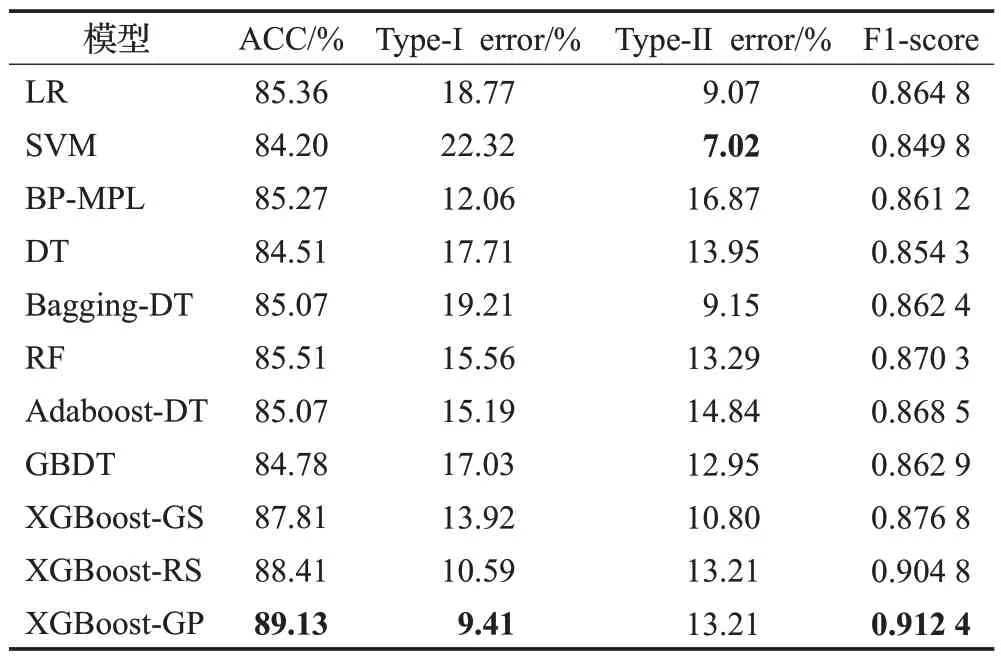
表6 在Australian数据集上模型准确性评估结果Table 6 Result of performances on Australian dataset on performance measures

在P2P-ren数据集上（见表7）XGBoost-GP模型在除了Type-Ⅱerror 之外的所有指标上都取得了最好的表现。ACC 相比表现最好的单分类器BP-MPL 高出0.91个百分点，比表现最好的集成分类器Bagging-DT 高出1.37个百分点。P2P-ren是三个数据集中正负样本数最不均衡的数据集，XGBoost-GP 模型将调解正负样本权重的参数scale_pos_weight设置为2，在保证Type-Ⅱerror的前提下，大大降低了Type-Ierror（4.08%），从而使得F1-score 有较大的提升（0.839 2），比表现最好的对比模型BP-MPL高出0.017 8。LR获得了最好的Type-Ⅱerror（4.24%），但Type-Ierror指标上表现较差，说明LR倾向于将样本判断为好样本，对违约行为的预测能力较差。在所有对比模型中，BP-MPL在ACC和F1-score指标上表现最好，可以作为一个备选模型。

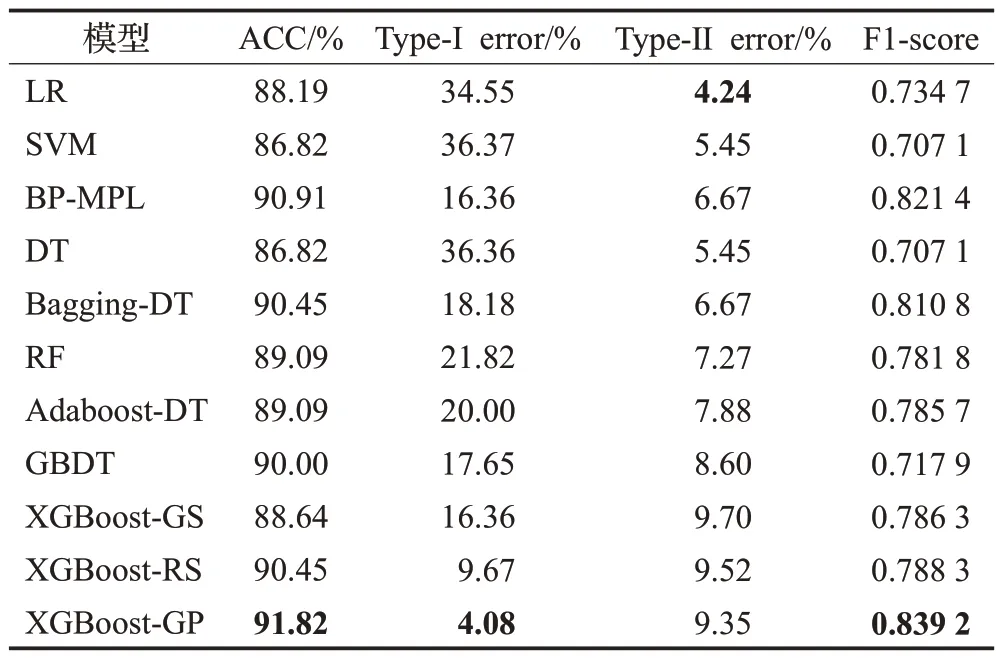
表7 在P2P-ren数据集上模型准确性评估结果Table 7 Result of performances on P2P-ren dataset on performance measures

总体上看，在所有数据集上，单个分类器中效果最好的是BP-MPL，集成分类器效果中最好的是XGBoost-GP。XGBoost-GP 在保证准确率的前提下能综合考虑其他各项指标，尤其是在降低Type-Ierror 和提高F1-score表现最好，说明XGBoost-GP非常用于适合信用评估领域，其对违约风险的预测同时保证了高精准和低遗漏。XGBoost 的scale_pos_weight 参数可以平衡正负样本权重，因此XGBoost在非均衡数据集上表现同样非常稳定，而贝叶斯高斯过程的超参数优化促进了XGBoost和信用评估数据特征之间的匹配度。

4.2 基于统计方法的模型对比分析

为了验证不同算法在统计意义上是否存在显著性差异，本文采用了非参数检验中的Firedman检验和后续检验Nemenyi 检验。Friedman 检验用于分析多组数据集上的多种算法的表现是否存在显著性差异。如果算法在统计学意义上存在显著性差异，可以使用Nemenyi检验进一步区分各个算法。

使用Friedman 非参数检验和Nemenyi 检验后续检验来验证不同模型在3个数据集上的ACC和F1分数是否存在统计意义上存在显著性差异。空假设表示模型之间没有差异。首先，Friedman 检验拒绝空假设表明模型存在显著性差异。如果存在显著性差异，再用Nemenyi 检验进一步区分各个模型。若两个模型的平均序值之差超出了临界值域CD，则这两个算法性能有明显差异。

表8 显示了11 个模型的ACC 和F1-score 在3 个数据集上的平均排名。Friedman检验结果显示11 个模型的预测准确率ACC 和F1-score 当显著性水平α=0.05时，拒绝原假设，在95%显著水平下有显著性差异。

表8 模型ACC和F1-score平均排名Table 8 Average rank for ACC and F1-score of models

采用Nemenyi检验进一步分析。当数据集数量为3，模型数量为11，α分别等于0.1，0.05 时，qα值分别为2.978，3.219。根据公式（19）计算得到CD值分别为8.064，8.717。其中N和k分别为数据集个数和模型个数。

图3和图4中柱形图代表了11个模型在3个数据集上的ACC 和F1-score 平均排名，按照排名的高低排序，两条水平线分别表示显著性水平分别为0.05和0.1时的CD值。水平线以上的模型比最优模型显著更差。如图3和图4所示，基于XGBoost的模型排在前4位，XGBoost-GP和XGBoost-RS排名最高，XGBoost-GS次之。在对比模型中，BP-MPL表现最好。集成模型优于单分类器模型LR、SVM和DT。

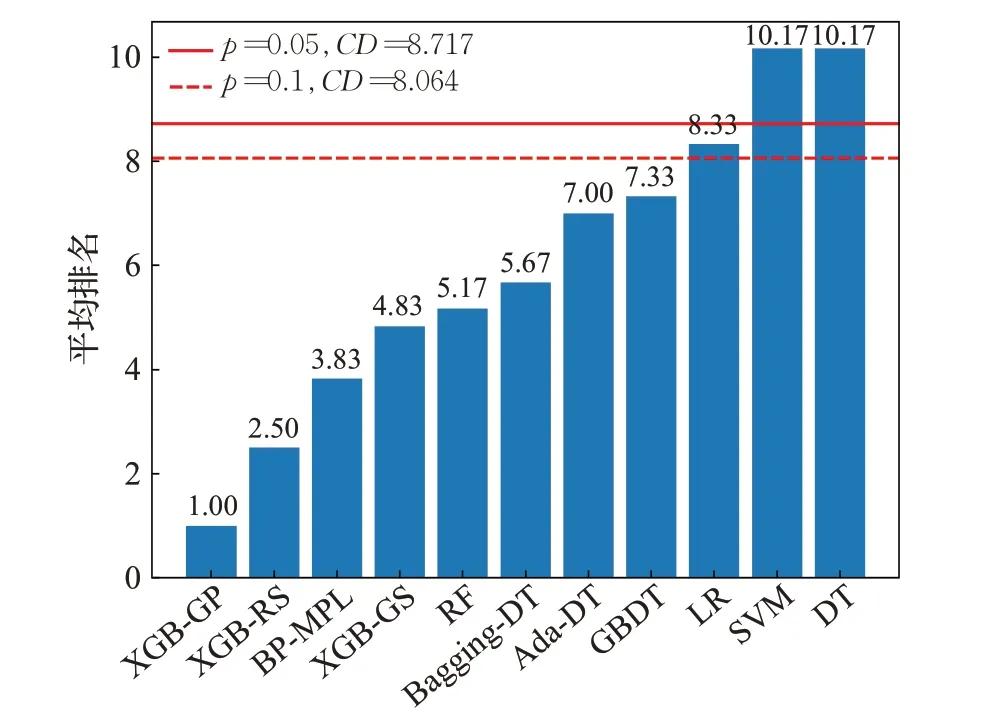
图3 模型ACC平均排名和Nemenyi检验结果Fig.3 Average rank for ACC of models and threshold of Nemenyi test

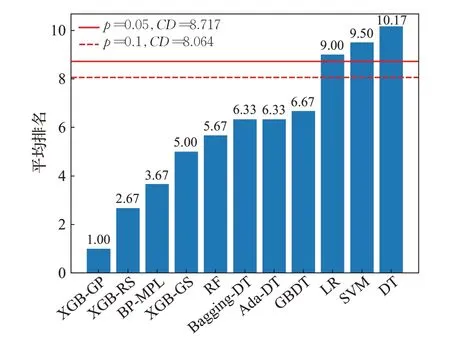
图4 模型F1-score平均排名和Nemenyi检验结果Fig.4 Average rank for ACC of models and threshold of Nemenyi test

4.3 超参数优化模型对比

评价一个超参数优化算法的优劣需要从时间复杂度和优化效果两个角度进行评判。超参数的评估代价很大，因为它要求使用待评估的超参数训练一遍模型。超参数优化算法的时间复杂度可以由使用待评估的超参数训练模型的次数来决定。依据表3 的XGBoost 超参数优化搜索空间，为了防止GS 搜索参数过多引起的维度爆炸，将Learning rate 和Number of boost 两个参数设置为固定值，则GS 用待评估参数训练模型的次数是16 000 次。RS 和GP 在所有超参数参与搜索、迭代500次，5折交叉验证的情况下，训练模型的次数分别为2 500 次和500 次。图5 显示了不同优化算法在三个数据集上超参数搜索时模型准确率的箱线图，可以看出GP搜索的超参数范围小，但效果总体优于GS和RS。

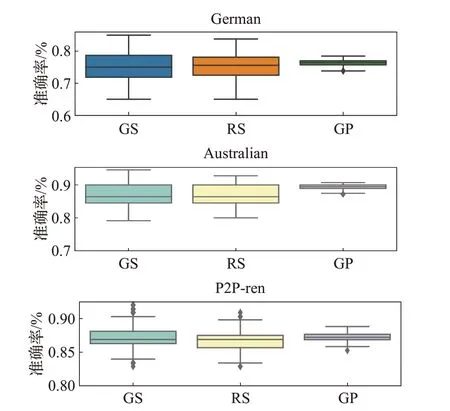
图5 三种超参数算法准确率箱线图Fig.5 Boxplot of accuracy over three hyper-parameter optimization approach

5 模型可解释性

模型的可解释性对于信用评估问题非常重要，具有更好的解释性的模型更容易被银行和其他金融机构的决策者所采纳。首先，具有可解释性的模型能够清晰地将决策过程呈现在贷款审批决策者面前[32]；其次，很多金融机构的决策者不喜欢集成学习模型，而更倾向于统计模型。具有很好解释性的集成学习模型更容易被接受[11]；最后，很多国家因为金融监管的原因需要有可解释性的模型[33]。基于XGBoost 的模型采用回归树作为基础模型，而树模型具有天然的可解释性。基于XGBoost的模型的可解释性依赖两个方面：特征重要性评分和决策规则。

其中特征重要性评分可通过算法的feature_importance参数获得。XGBoost-GP 在P2P-ren 的特征重要性分数如图6所示。

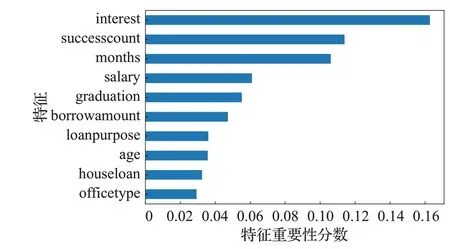
图6 XGBoost-GP在P2P-ren上的特征重要性分数Fig.6 Diagram of feature importance scores on P2P-ren

特征重要性分数体现了该特征的权重，分数越高，表明该特征在模型决策过程中的作用越重要，那么在信用评估的信息采集过程中需要被重点采集。相反的，特征重要性分数低的特征可以去掉以提高算法效率。

通过查看XGBoost 每一棵决策树可以清晰地看到模型的决策规则。XGBoost模型的基模型是归回树，每一次迭代产生的新树用来拟合上一个归回树产生的残差，最后对样本的预测值取决于所有回归树叶子节点值的和。通过sklearn的plot_tree（）函数可以查看XGBoost模型每一次迭代产生的回归树，图7显示了XGBoost-GP在P2P-ren上的第一棵决策树和最后一棵决策树。

图7 XGBoost-GP 在P2P-ren上的决策树Fig.7 Decision chart of XGBoost-GP on P2P-ren

6 结束语

本文将一种非常高效的集成学习方法XGBoost 用于信用贷款的实际大数据预测中，并分别使用网格搜索、随机搜索、贝叶斯优化高斯过程三种方法对XGBoost进行调参优化，考察其在German、Australian和中国网贷平台信用风险预警问题上的效果。通过和其他机器学习方法（LR、SVM、BP-MPL、DT、Bagging-DT、AdaBoost-DT、GBDT）进行对比，考察了ACC、Type-Ierror、Type-Ⅱerror、F1 分数四个指标，实验结果表明XGBoost-GP 各项性能表现优异，尤其在风险评估最重视的违约样本召回率方面表现最为突出。通过Friedman 检验和后续检验Nemenyi 检验，证明这XGBoost-GP 方法在统计学意义上具有明显优势。同时，基于XGBoost的方法在特征选择和决策规则可以显性地显示出来，模型具有可解释性，可以为信用贷款风险评估提供有效而可靠的方法。

贝叶斯超参数优化是一种基于已有样本点的先验知识来探索新的更优超参数的优化过程，具有收敛速度快，对非凸问题依然稳健的优点，极大地提升了XGBoost的性能。XGBoost是高性能的集成学习模型，自带缺失值处理和并行计算能力，速度快，精度高，同时具有可解释性，样本特征值重要性和决策规则一目了然，作为信用风险评估模型更容易被银行等金融机构所接受和采纳。信用风险评估是一个典型的样本不均衡问题，数据不均衡对模型的预测准确率有一定的影响，本文只在算法层面对正负样本的权重进行了设置，没有在数据层面做出重采样或降采样的处理。未来可进一步探讨从数据层面和算法层面结合处理样本不均衡问题，提高信用贷款违约风险评估模型的预测准确率。