面向实际工况的AGV局部路径规划及跟踪研究

吴 斌，张 新，VIALOVA Varvara

南京工业大学 经济与管理学院，南京 211816

随着“工业4.0”“中国制造2025”的发展，各种智能设备在制造领域应用越来越广泛。叉车型AGV作为自动搬运工具，在生产系统、物流系统中可以轻松搬运各种物料，实现物料搬运的自动化，提升物流效率，降低物流成本。但AGV 虽能实现托盘的自主拾取，其工作效率和拾取精度却会因行走路径的不同存在较大差距。优良的路径能使得AGV 行走过程中不易抖动、花费时间短且易于跟踪。而差的路径虽然能使AGV到达指定目标点，但可能会使AGV在行走过程中抖动严重、频繁大幅度转弯、行走时间长、跟踪效果较差，并容易引起叉车堵塞、货物坠落等问题。因此，对叉车型AGV的规划路径深入研究对提升AGV 运行效率、精度和安全性意义重大。

AGV路径规划问题可以分为全局路径规划与局部路径规划。全局路径问题以已知全局环境出发，在起点与终点间规划出符合目标函数最优的无碰撞路径，目前已取得丰富的研究成果，常用算法包括A*算法[1-2]、蚁群算法[3]等。但这些研究方法注重考虑全局环境约束，缺少对于局部环境不确定性和路径跟踪可行性的考虑，而局部路径规划能很好地解决上述问题。AGV的局部路径规划重点关注AGV 当前所处局部环境的信息，在AGV当前位置与目标位置间规划出一条能满足运动约束及局部环境约束的曲线路径，主要研究方法有人工势场法[4-5]、神经网络算法[6-7]、动态窗口法[8-9]及参数曲线拟合法[10-14]等。由于AGV进行托盘拾取作业时，起点位姿及托盘位姿存在不确定性，属于未知的局部环境信息，因此属于局部路径规划问题。

多数AGV的局部路径规划问题实际就是局部环境避障问题，即对于检测到的意外障碍物，如何规划局部的路径进行避障。而解决叉车型AGV托盘拾取的局部路径规划问题时，由于货叉与托盘对接精度要求高，相较于避障，其更注重起始点和终止点的位姿约束及路径跟踪精度。托盘拾取路径规划相关的文献较少。吕恩利等[15]提出了基于B 样条曲线的叉车托盘拾取路径规划方法，综合考虑叉车运动约束和托盘对接精度等约束，以路径曲率最小化为优化目标求解出了托盘拾取路径。文献[16]及文献[17]同样采用了参数曲线拟合法成功解决了路径规划中的起止点位姿约束的问题。因此，参数曲线拟合法适合作为托盘拾取路径规划的基本方法。但是，现有文献的研究成果尚无法完全应用于实际工况下的AGV 托盘拾取作业场景中。文献[15]以最小化最大曲率为优化目标，但实际工况中为了提高AGV工作效率，相较于最小化曲率，规划路径时更多以最小化路径长度为优化目标。在起止点间位姿差距较大的情况下，以最小化最大曲率生成的路径过长，较大地增加了AGV 的行驶时间。文献[16]以路径最短为优化目标设计AGV的路径，但其应用场景不为托盘拾取，对于位姿误差要求低，且没有使用跟踪算法进行实际路径跟踪验证，因此路径无法直接应用于托盘拾取场景中。文献[17]以路径最短作为优化目标，依据B 样条曲线生成路径，并进行了跟踪验证。但其研究针对拖拉机的轨迹跟踪，相较于AGV的托盘拾取，对终点位姿误差的要求同样较低，因此其路径不能完全被托盘拾取场景所应用。

综上所述，本文研究目的在于设计一套路径规划及路径跟踪算法，使得即使在起止点间初始偏移距离和航向角差值较大的情况下也能规划出长度尽可能短、托盘对接精度尽可能高的托盘拾取路径，并使得路径能被精确地跟踪。本文的创新点在于：对于路径规划问题，设计满足实际工况条件的约束集及路径评价函数，运用粒子群算法进行路径求解；对于路径跟踪问题，选取合适的跟踪算法并进行改良优化，提高跟踪精度。

1 问题描述

AGV 在拾取托盘时有两种行驶方式，即正向行驶和反向行驶。如图1、图2 所示。当AGV 正向行驶时，无须调整货叉方位便可直接接近托盘，但其缺点在于，当横向偏移距离较小时，AGV 极有可能因为其最小转弯半径及始末航向角约束使得其无法顺利到达目标点。图1中，由于D较小，且AGV在起点处与垂直方向存在角度差β，因此叉车无法到达P1点。当AGV反向行驶时，以图2 为例，先从起点A行至B点处，再从B点行至目标点P1。其路径可分为两段，一段为调整货叉方向的缓冲路径，一段为托盘拾取路径。反向行驶的好处在于，当托盘位于距离AGV 很近的P1点时，不会发生因航向角及最小转弯半径的约束使得AGV无法抵达目标点的现象。因此，AGV 的两种行驶方式都有其存在的必要。

图1 AGV正向行驶示意图Fig.1 Diagram of AGV’s driving forward

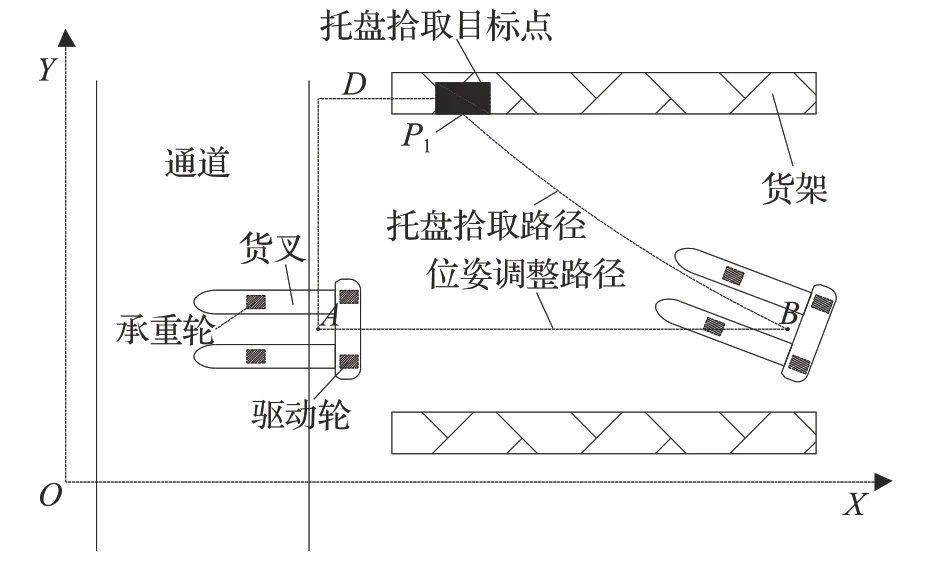
图2 AGV反向行驶示意图Fig.2 Diagram of AGV’s driving backward

但是实际工况中，无论选择何种行驶方式驱动AGV，在缺乏正确规划及跟踪算法的情况下，托盘拾取作业过程中总存在如下主要问题：路径拐点附近AGV车身摆动幅度较大；AGV 在行驶过程中车身抖动较为严重；AGV虽能接近托盘目标点，但其与托盘间的横向误差及朝向角误差较大，导致货叉与托盘孔不能很好地对接。以上问题严重影响了AGV托盘拾取工作的精度及效率，使得AGV 托盘拾取作业的自主性无法得到实现。因此，为解决以上问题，必须为AGV设计正确的路径规划算法，同时对现有的跟踪算法进行改进。

综上所述，为解决现存路径问题，本文基于叉车型AGV 的两种行驶方式，提出相应的路径规划和跟踪控制方法，并通过不同工况环境的仿真实验验证算法的可行性和优越性。

2 AGV运动及跟踪模型

为方便后续路径规划及跟踪算法的设计，以正向行驶为例，建立AGV 的运动及跟踪模型。以后轮为驱动轮，前轮为承重轮，建立AGV运动及跟踪模型如图3所示。

图3 AGV运动及跟踪模型图Fig.3 Motion and tracking model of AGV

其中，1 为AGV 驱动轮，2 为承重轮，3 为等效后车轮，4为等效前车轮。设AGV的等效前车轮能随路径轨迹从点B运动至点C，则模型中变量的定义如表1所示。

表1 运动及跟踪模型的变量说明Table 1 Variable description of motion and tracking model

则根据以上变量可推出运动学模型公式如下：

3 叉车型AGV局部路径规划算法

3.1 B样条曲线

B样条曲线因其优秀的性质[18-19]被广泛应用于局部路径规划。B样条曲线方程如下所示：

其中，参数u取值范围为[0，1]，xi为曲线控制点，Ni,p(u)表示第i个p次B样条基函数。B样条曲线实际由数段贝塞尔曲线构成，其相较于贝塞尔曲线的优点在于B样条曲线支持局部的修改，且其曲线拼接处能轻松满足几何连续条件。三次均匀B样条曲线表达式如下所示：

则三次均匀B样条曲线的一阶、二阶导数如下所示：

3.2 面向实际工况约束的托盘拾取路径规划

3.2.1 起止点位姿约束

设托盘拾取路径的起点坐标为Ps(x1,y1)，航向角为θs。终点坐标为Pd(x2,y2)，航向角为θd，为了使得路径曲线能够满足托盘拾取起始点和目标点的航向角约束，同时减少曲线参数求解量，曲线的6个控制点坐标求法分别如下[20]：

其中，L1和L2为待确定的路径参数，由优化算法求得。

3.2.2 曲率连续性约束

若路径曲率不连续，会使得AGV 在行驶过程中出现车身频繁抖动、轮胎磨损过度的现象。由曲率公式（3）可知，欲使得路径曲率连续，需保证样条曲线二阶可导。由公式（12）可知，三次均匀B样条曲线二阶导数连续，可以使得求解得到的曲率拥有连续的性质。另外，B样条曲线在曲线拼接处也能使得曲率连续，即规划路径拥有C2 连续的性质，所以三次均匀B 样条曲线能够满足规划路径的曲率连续性约束。

3.2.3 AGV运动性能及工作环境约束

为使得AGV在实际横向偏移距离及航向角差距较大的场景下行至终点的位姿仍能保证货叉顺利与托盘对接，同时符合自身运动性能约束，以AGV自身局部坐标系为参考方位，给出如下约束规划集：

其中，(as,bs)为路径起点坐标，(ad,bd)为终点坐标。ℓ为曲线的曲率集合，r0为AGV 的最小转弯半径，yd为与目标托盘所在货架相对的货架纵坐标值，yr为生成路径坐标点的纵坐标集，δ为AGV 车轮的转向角度，θmax为AGV 车轮所允许的最大转向角度。k1及k2都为恒定常数，其取值分别由实际工作场景环境确定。自上而下，式（a）保证路径曲率不超过AGV最小转弯半径的倒数，式（b）与式（c）保证AGV在货架间行驶时，路径不与货架产生碰撞，式（d）保证AGV车轮转角不超过最大转角。当路径取值点数较少时，式（e）使得起始点附近的路段较为平缓，防止AGV 在路径跟踪一开始就产生较大的抖动。

3.2.4 多目标路径评价函数

若简单将最短路径设置为优化目标，则路径能到达理想情况下的最优，但其首末端可能由于曲率过大，实际工况中AGV 无法准确运行，因此必须考虑多目标优化情况。多目标优化问题一般以帕累托最优解集形式给出，但是考虑实际工况下AGV 运行的实时性和方便性要求，需要从给出的帕累托最优解集中，通过设置权重的方法选定合适的单一解。因此直接对多目标评价函数设置权重，将其转为方便处理的单目标评价函数。假设路径共由n个点拟合构成，则关于生成路径的目标评价函数如下：

目标评价函数z由三部分组成：路径近似长度、目标点附近曲率绝对值的最大值和目标点附近路径曲率变化程度。其中，ω1至ω4为权重参数，Length为规划路径的近似长度。第二部分中的ℓ(s:n)表示靠近目标点处的部分路径曲率集合，第三部分中的ℓ(j)-ℓ(j-1)表示靠近目标点处的部分路径曲率变化值的集合。这两部分作用为将接近终点处的路径转弯点提前，使得AGV在实际跟踪中不会因终点附近曲率过大而导致跟踪效果不佳。当路径拟合点数较少时，评价函数的第三部分可以使得路径转弯点提前。但当拟合点数较多时，点间曲率变化值已经较小，第三部分不再发挥有效作用，因此必须加入第二部分使得在此种情况下评价函数也能挑选出合适路径。算法对于以上三部分的实际寻优方式分别为：使得路径长度尽可能小；使得终点附近路径曲率最大值的绝对值尽可能小；使得终点附近路径曲率变化值的最大值的绝对值尽可能小。该三部分同为最小化函数值问题，因此可以通过取权重的方式将其转换为单目标优化问题，从而得到单一的解。此外，由于函数中三部分的量纲有差距，为了使得三部分的变化对整体评价函数有较为平等的影响，一个简单的对策为将三部分的实际变化值乘以合适的系数，使得三部分的最终变化值在同一个量纲下。通过多次仿真实验得出，将第一部分的实际变化值缩小10 倍，第二部分的实际变化值保持不变，第三部分的实际变化值放大10 倍能取得较好的评价效果，因此设置参数k3及k4，取值分别为0.1及10，而对于公式中的权重值，则通过仿真实验进行选取。综上，整理出最终的目标评价函数如公式（20）所示：

3.3 基于粒子群算法的局部路径参数优化

路径曲线的形状由其控制点决定。AGV正向行驶时，依据3.2.1小节规定的控制点确定方法，可以使得待优化参数减少为2个，即只需确定L1与L2的值即可确定整条路径。当AGV 反向行驶时，其路径求解方法如图4所示。首先，以AGV当前位置S为起点，以货架中最接近起点的托盘位置为目标点，起点航向角固定为0 rad，终点航向角取实际值代入优化算法。若优化算法以起点S坐标、目标点P坐标及规定起止点航向角为基础在迭代一定次数后无法求解出符合条件的路径，则将起点横坐标往后平移相应合适距离，再进行寻优，直到满足要求，得到点S′。若S点无须迭代即可导出合格的路径，则直接将S点作为S′。

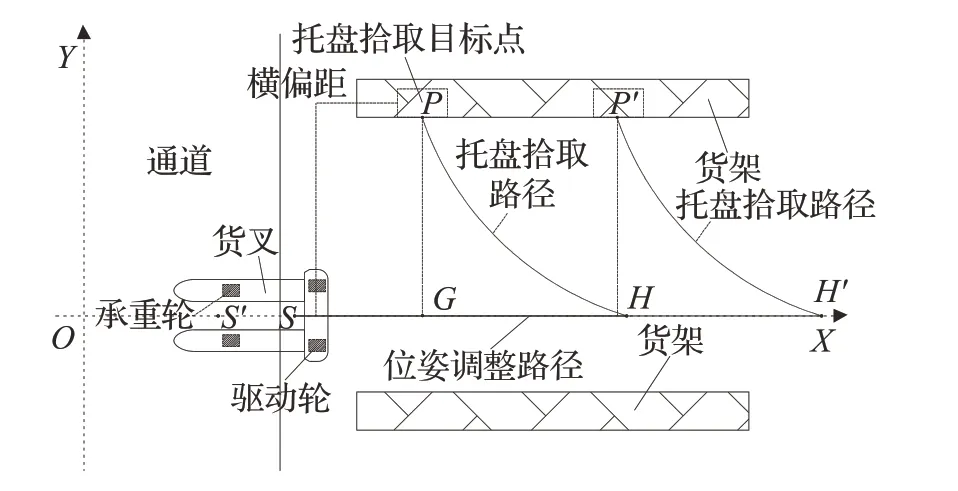
图4 AGV反向行驶路径寻优示意图Fig.4 Path optimization of AGV’s driving backward

其中，设初始起点坐标为S(a,b)，最接近AGV的托盘坐标为P(c,d)，迭代后的新起始点坐标为S′(m,n)。

确定了点S′后，若托盘P位于货架最左端附近，则在x轴上寻一点H，使得其与点S′关于点G(c,0)对称。则AGV 从起点S行驶至点H(2c-m±kd,n)即可进入托盘拾取路径。若托盘离AGV 较远，设此时托盘P′坐标为(j,k)，则将点H坐标修改为H′(j+c-m±kd,n)即可。kd为一常系数，代表一小段缓冲距离，取值由初始点相对货架的方位确定。

综上所述，反向行驶的AGV行走路径以点H或H′为界限划分为两段。以目标点P为例，则完整规划路径由曲线SH及曲线HP构成。AGV先以等比例反馈控制法由S点行驶至H点，再以H点为起始点，托盘拾取点为目标点，跟踪规划出的相应B样条曲线路径到达终点。此种方式能解决AGV因最小转弯半径约束导致的无法抵达目标点的问题，且路径长度接近最优。

本文采用粒子群算法作为路径参数求解的优化算法，其惯性系数及速度迭代公式如下所示：

其中，ω为惯性系数，ωmax、ωmin分别为惯性系数最大值和最小值，k为算法当前迭代代数，T为算法迭代总次数。vi(k)、xi(k)分别为第k次迭代时第i个粒子的速度和位置，c1、c2分别为个体认知系数和社会认知系数，r1、r2为0至1之间的随机数。pibest、gbest分别为粒子局部最优位置和全局最优位置。粒子群算法的迭代流程如下：

（1）初始化由路径参数L1及L2构成的粒子种群矩阵，初始化粒子速度矩阵。

（2）根据初始化种群解，解出对应曲线方程，并计算其路径长度及曲率集合。

（3）将路径长度和曲率集合代入公式（20），求解出初始适应度值，记录最小适应度值及其粒子的位置。

（4）判断是否满足迭代终止条件。是则退出循环，否则继续迭代。

（5）解出粒子种群矩阵所对应的曲线方程，依据公式（20）计算出适应度值，记录最小适应度值及其粒子的位置。

（6）对局部最优值及全局最优值进行比较和更新。

（7）依据公式（21）进行粒子速度及位置的更新，得到新的种群矩阵。

（8）令迭代次数增1，返回步骤（4）。

4 路径跟踪控制算法

跟踪算法的目的在于依照规划的路径和跟踪对象的各类参数，根据一定步骤计算得出规定周期内跟踪对象的控制量，包括速度、车轮转角等[21-25]。纯跟踪法在叉车型AGV 行走速度较慢的情况下，其跟踪效果较为理想。但是，纯跟踪法的缺陷在于其无法对航向角偏差实行有效控制，因此可能会导致AGV 实际停止的位姿与目标位姿间存在不可忽视的误差。另外，预瞄距离取值也非常影响纯跟踪法的跟踪效果。因此需对纯跟踪算法进行相应的改进和补充，以形成完整的、精度更高的跟踪算法。

4.1 前视距离的改进

原始纯跟踪法中的前视距离公式大多由如下表达式决定：

其中，Ld表示预瞄距离，kv为速度系数，v为当前车辆行驶速度，L0为预瞄距离下限值。由于本文研究AGV的行驶速度较小，因此对于固定的L0,Ld的变化范围较小。若Ld的取值较大，则AGV在跟踪路径时将不易产生抖动，跟踪更为自然，但缺点是在一些曲率较大的路径转角，会出现转向不足的现象从而产生危险。若Ld取值较小，则能保证可以较为安全地通过曲率较大的弯道，但在整体路径跟踪上抖动较大，不利于跟踪。因此，必须设置动态的Ld，使之能随路径的变化而变化。本文提出一种确定Ld的方式如下：

其中，index为AGV 参考路径上距离AGV 当前实际位置最近点的序号，curv(index)代表该点处的曲率，k5为一常系数。依照该方法确定预瞄距离，可以使得Ld随路径曲率的变化而动态变化。

4.2 航向角误差消除

考虑到AGV 通过纯跟踪法控制后，与目标点间位姿的差距已经变小，因此在使用纯跟踪法控制AGV 使得其与目标点间位姿差距减小至一定程度后，可以采用更为直接的航向角控制法对AGV 实行控制，直到其位姿误差能满足精度要求。控制方法如下：

其中，θdest为目标航向角，θreal为当前AGV 实际航向角，k6为一常系数。位置误差计算公式如下：

其中，dx与dy分别为AGV当前位置横、纵坐标与目标点位置横、纵坐标之差。

4.3 AGV控制量求解

因为此种AGV 属于四轮车结构，因此等效转向角需进行换算转变成AGV左右侧车轮的转角：

其中，δi与δj分别表示AGV的左侧车轮与右侧车轮转角，L代表前后轮轴距，R代表转向的等效转弯半径，d代表驱动侧车轮间的轮距。

综上所述，本文路径规划及跟踪控制算法流程如图5 所示。AGV 首先通过激光传感器定位得到起始点位姿，随后获取目标托盘的位姿，依据横向偏移距离选择行驶方式，若正向行驶，则通过规划算法求解出相应路径，最后采用改进跟踪控制算法进行跟踪。若反向行驶，则通过规划算法求解出位姿调整路径和托盘拾取路径，合并生成完整的路径，最后采用改进的跟踪控制算法进行跟踪。

图5 叉车型AGV路径规划及跟踪算法流程图Fig.5 Flowchart of path planning and tracking

5 实验分析

5.1 问题背景

叉车型AGV 接到托盘拾取命令后，首先行驶至目标托盘所在货架位置，随后通过激光传感器识别和托盘识别技术获取自身位姿及托盘位姿。最后依据托盘拾取局部路径规划算法，在起点和目标点间规划出一条最优路径并跟踪。其工作场景图如图6所示。

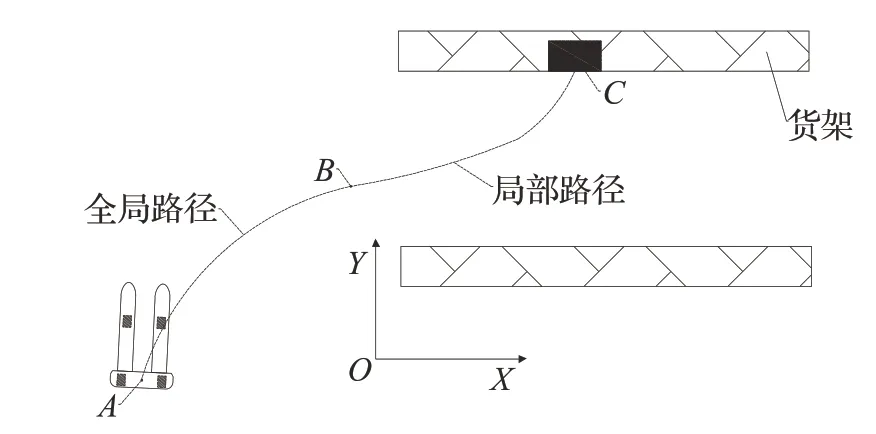
图6 AGV托盘拾取工作场景图Fig.6 working scene of pallet picking

图6 中，AGV 接到托盘拾取命令后，按照全局路径由A点行至B点，随后启动托盘拾取路径规划算法，在B与C间生成局部路径，追踪路径直至到达目标点C。

5.2 仿真参数设置

本文参照实际的工况环境对仿真参数进行设置。坐标系以图6 中坐标系为参照，设定沿x轴正方向为0 rad，角度以逆时针方向增长，则沿y轴正方向为π/2 rad。其具体仿真数据如表2所示。其中，第一行至第四行为AGV 的重要运动及尺寸参数，第五行至第九行为AGV工作环境的设置。第十行至最后为规划及跟踪算法的重要参数。

表2 仿真参数设置表Table 2 Simulation parameters

5.3 路径评价函数权重值选取

路径评价函数的权重实际决定了终点附近路径的弯曲程度，从而影响最终的跟踪误差。因此确定权重的思路为：根据托盘及货叉的匹配要求，分别确定横向对接误差及航向角误差的一个最大允许值，再分别选取权重代入求解路径，使用跟踪算法进行误差检验，以误差值为权重选取的依据。通过初步仿真实验发现，当ω1取值为0.9 左右时，此时无论ω3如何取值，跟踪算法得到的最终横向对接误差及航向角误差都较大。而当ω1取值0.8 左右及其以下时，跟踪算法得到的最终航向角误差都很小，且符合精度要求。因此航向角误差已经无法起到比较权重的作用，此时只能依靠横向对接误差的对比来确定权重。因此，设定横向对接误差为权重选取的主要依据。设定横向对接误差最大允许值为G。考虑到权重确定工作的方便性，以0.1 为间隔对权重进行选取及测试。结合现场实际并与相关技术人员讨论后，确定G值取0.024 m，即最终托盘孔与货叉的横向对接误差不大于0.024 m时，能保证托盘拾取工作的精准度。为了使得跟踪误差在起止点间位姿差距较大的情况下也能满足限制，仿真实验选取起点位姿(0 m,0 m,-π/6 rad)，终点位姿(9 m,6 m,7π/12 rad)，几组仿真对照结果如表3所示。

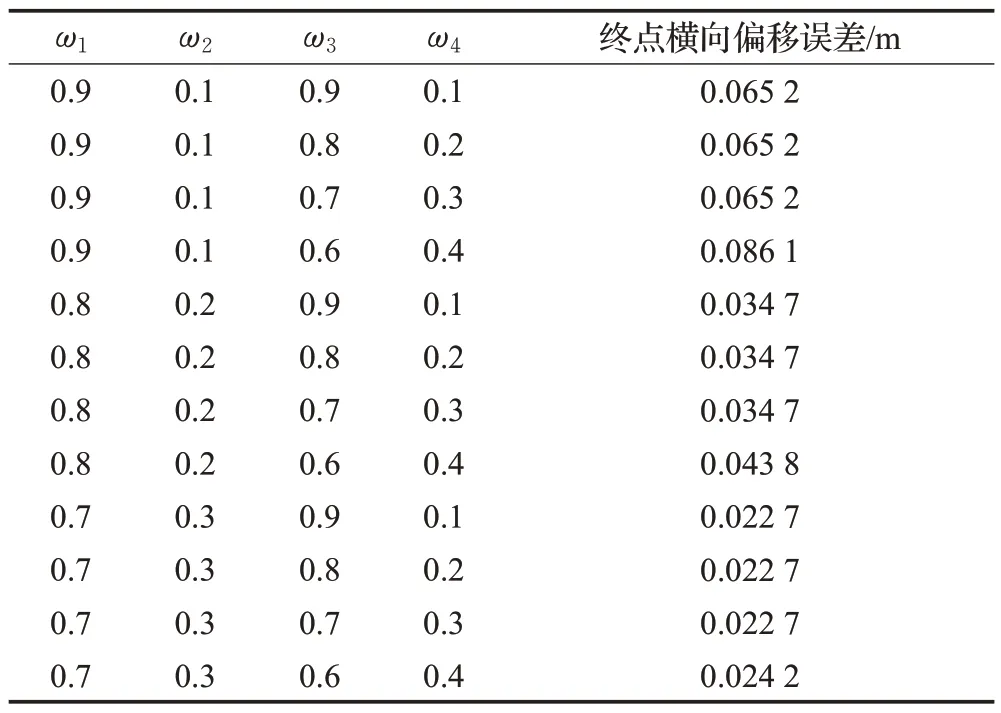
表3 目标函数权重实验表Table 3 Experiment of weight

由仿真数据可知，当ω1减小，ω2增大时，终点横向跟踪误差显著减小。当ω1及ω2保持不变，ω3减小，ω4增大时，终点横向跟踪误差变大。当ω3取0.9、0.8、0.7时，跟踪误差稳定。直到ω3取到0.6 时，跟踪误差进一步增大。结合G值和仿真数据，当ω1、ω2、ω3、ω4分别取0.7、0.3、0.7、0.3时，使得终点横向跟踪误差为0.022 7 m，能很好地符合托盘孔与货叉的对接精度。则依据公式（20），取ωa为0.7，ωb为0.21，ωc为0.09。最终确定路径的目标评价函数Z如公式（27）所示：

5.4 改进跟踪算法的仿真对比

选取同样规划路线，为使得AGV 跟踪路径时振荡较小，选取同一个较大的前视距离值为1.2 m，原跟踪算法和本文跟踪算法的理想跟踪情况如图7。

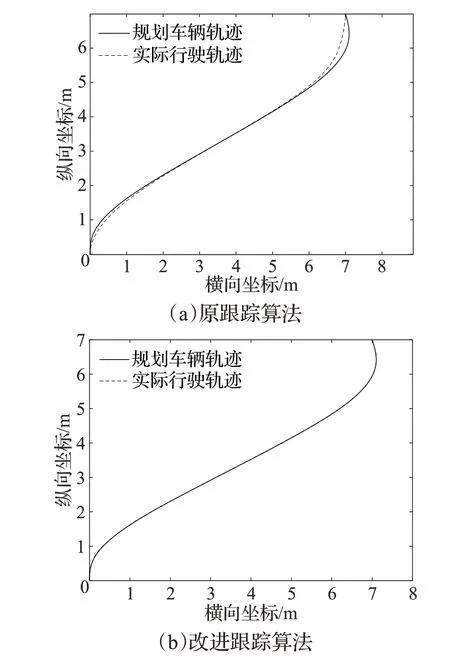
图7 跟踪算法对比图Fig.7 Comparison of tracking algorithms

由图7可知，对于同一个前视距离，（a）中AGV在起点和终点拐点处明显存在转向不足的情况，且行至终点处的车身航向角明显与终点朝向角不一致，严重影响托盘拾取精确度。（b）中由于实现了预瞄距离随路径曲率及跟踪速度的动态变化，且添加了航向角控制法，使得AGV 在曲率较大的拐点处也能很好地进行路径跟踪，同时到达终点处的车身朝向角与终点朝向角一致。因此，改进的跟踪算法能有效提高AGV实际路径跟踪的精度。

5.5 实际工况下规划算法跟踪对比分析

实际路径跟踪之所以会和规划路径存在偏差，是因为AGV 自身硬件、控制系统及实际工作环境综合导致的。在横向偏移距离、航向角差值较小的情况下，则文献[15]的路径规划算法效果较好。但若以路径长度最小为优化目标，则横偏距及航向角差值越大，其规划路径的不稳定性越大，导致跟踪误差变化也越大。令L1与L2为以路径最短为单目标优化函数的原算法求解参数，与为本文算法求解参数。设置起点坐标局部不变，通过改变终点坐标及起止点朝向角考察仿真结果。对于正向行驶，为了加大仿真的场景规模以更好验证规划算法的优越性，设计正交实验进行验证。将终点坐标、起止点朝向角视为三个因素，以朝向角变化范围为参照，统一将三因素设置为五水平。选用L25(56)正交表，场景按照限定范围采取正交表设计仿真。若在某些仿真场景下无法求解出合适的路径参数，则在表格中以“无解”体现。若能求解出路径参数，则将求解结果填入表格中。最终规划工况仿真数据及算法求解结果如表4所示。

表4 仿真场景参数及求解结果Table 4 Parameters of simulation scene and results of algorithm

由表4 可知，对于场景1、2、3 及6，两种算法均无法规划出合适的路径，这是因为以上场景起始点和目标点间的初始横向偏移距离较小，而航向角差距较大，导致路径的最大曲率无法满足AGV 的最小转弯半径约束。对求解出的两种路径进行跟踪对比验证，其终点横向偏移误差及航向角误差如图8 及表5 所示。其中，将跟踪算法取得的误差值设为实际值的绝对值。由于表4中，场景1、2、3、6 无法求解出合适路径，因此在表5 中不对以上场景进行跟踪测试。

表5 终点跟踪误差对比Table 5 Comparison of tracking error for end point

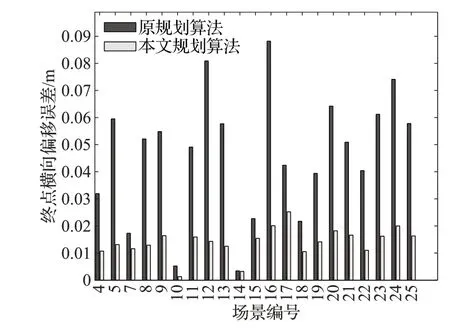
图8 两种算法终点处横偏距对比Fig.8 Comparison of lateral error

图8 中，场景7、10、14、15 下，原规划算法与本文规划算法的终点处横偏距差距较小。对于场景10、14、15，这是因为起止点间的航向角差距较小、行驶方向与起止点的连线方向相差较小所导致的。对于场景7，由于起止点的航向角位于不同象限导致AGV 存在调头现象，同时初始横偏距较小，导致两种路径终点附近曲率差距较小，因此终点横偏距差距较小。除去以上特殊场景，余下的大量场景中，原算法与本文算法得到的最终横偏距差距较大，且改进的跟踪算法使得AGV 跟踪本文规划算法得出的路径时，能在终点处取得更小的航向角误差。

选取表3 中的典型场景16 进行规划及跟踪效果的详细分析。其粒子群迭代曲线、跟踪效果对比、航向角变化情况如图9、图10、图11所示。

图9 场景16粒子群算法迭代过程Fig.9 Iterative process of particle swarm optimization for scenario16

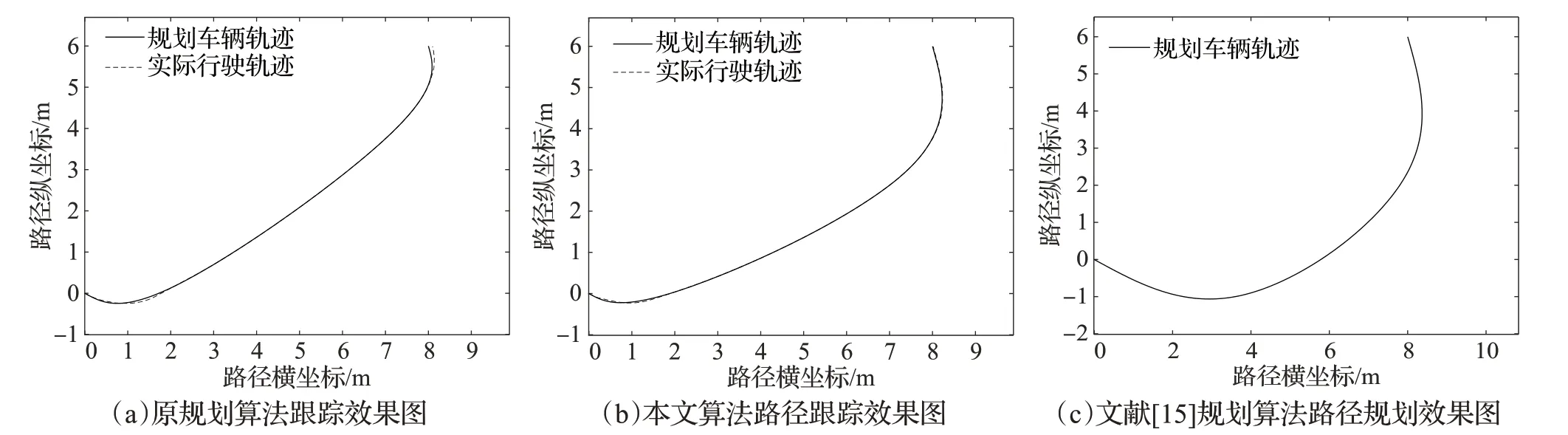
图10 场景16规划路径跟踪效果对比图Fig.10 Comparison of tracking effect for scenario 16

图11 场景16规划路径航向角变化对比图Fig.11 Comparison of heading changes for scenario 16

由图9 知，在对场景16 进行求解的过程中，当算法迭代到40 次左右时，目标函数能收敛至最佳值。实际对表4中的所有场景进行优化求解时，迭代曲线显示算法总能在迭代至约40代或之前时收敛至最佳值。由于篇幅限制，因此文章仅对典型场景16 的算法收敛曲线进行展示。

由图10（a）可知，AGV 在跟踪至第一个拐点附近时，由于曲率较大发生明显偏移，之后偏移量收敛。而终点附近曲率再一次变大，使得AGV 再次发生明显偏移，最终导致实际停留点与目标点间的误差较大。其中，横向偏移距离为0.088 2 m，航向角误差为4.3×10-3rad，托盘对接误差较大。由图10（b）可知，AGV在跟踪本文算法规划的路径时，在第一个拐点附近同样产生明显的偏移，之后误差收敛。但终点附近曲率较小，使得AGV能更为精准地跟踪终点附近的路径。最终横向偏移距离为0.020 1 m，航向角误差趋向于0 rad，能很好地满足托盘拾取的精度要求。由图10（c）可知，文献[15]规划算法得到的路径虽然能使得路径全局曲率更小，但在起止点间初始位姿差距较大的情况下，会使得路径长度过大，因此增加了路径的行走时间，降低了托盘拾取工作的效率。图11 中，AGV 在跟踪本文算法规划出的路径时，其航向角变化曲线基本位于跟踪原算法规划出的路径的航向角曲线下方，能较好地提高AGV 的跟踪稳定性。

为验证AGV 反向行驶规划方法的可行性，设计3个仿真场景如表6所示。其求解、最终跟踪结果如表7、8所示。

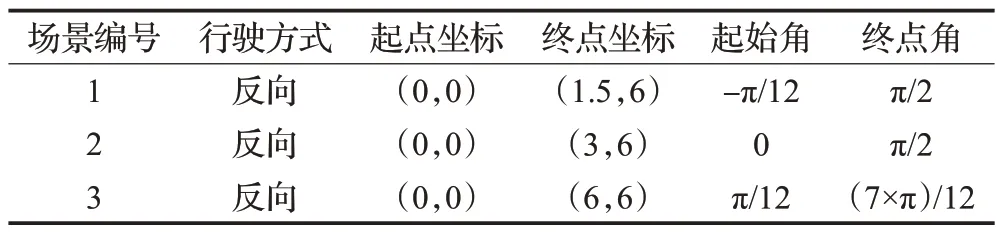
表6 算法仿真场景参数Table 6 Parameters of simulation scene

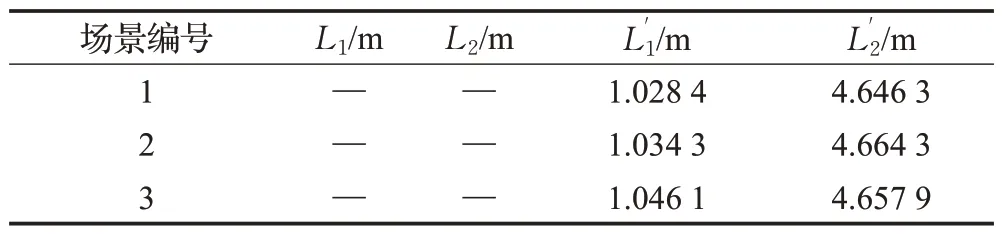
表7 算法仿真求解表Table 7 Results of algorithm

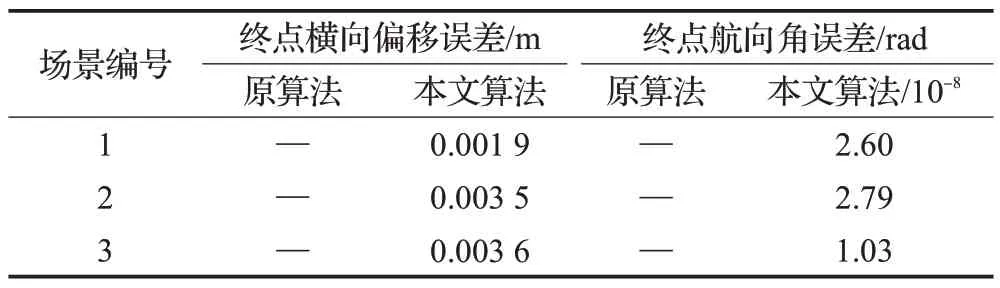
表8 终点跟踪误差对比Table 8 Comparison of tracking error for end point

其中，选取典型场景1 进行跟踪分析，其跟踪效果图、航向角变化情况如图12所示。

图12 场景1规划路径及跟踪数据图Fig.12 Path planning and tracking data for scenario 1

由图12（a）可知，AGV在行驶至曲率较大的一段路径时，与规划路径出现明显的偏移，随后路径曲率减小，跟踪误差收敛。误差收敛后的跟踪路径与规划路径高度重合。图12（b）中，托盘拾取路段航向角变化平滑自然，使得AGV跟踪路径的精度更高，能较好地满足托盘拾取工作的精度约束。

综合以上分析，本文基于文献[16]、文献[17]的规划算法进行了改进，使得其能应用于托盘拾取工作场景中，同时重新设计了跟踪算法以提高AGV 路径跟踪的准确度。相较于文献[15]的托盘拾取路径规划算法，本文提出的规划及跟踪算法能保证即使在起止点间位姿差距较大的情况下，AGV 仍能与托盘孔进行平稳且精确的对接，同时使得规划路径尽可能短。因此本文算法能更好地应用于实际工况下的托盘拾取作业场景中。

6 结束语

针对实际工况中叉车型AGV托盘拾取局部路径规划与跟踪问题，以B样条曲线为基础，综合考虑AGV运动约束、起止点位姿约束及场地限制等约束，设定路径长度最短为主要优化目标，设置不同的初始横向偏移距离及航向角差值，建立实际工况下叉车型AGV 托盘拾取的多约束、最小化目标代价函数的路径规划模型。以纯跟踪法为基础，考虑前视距离和航向角误差，建立融合纯跟踪法和航向角控制法的路径跟踪算法。路径规划及跟踪控制算法仿真的结果表明，本文的路径规划算法能较好克服起止点间横偏距及航向角差距较大导致的实际工况下叉车型AGV 托盘拾取精度不佳的问题，且跟踪算法使得AGV能更精确地跟踪规划路径。