复杂网络与GA-PSO算法下的癫痫脑电识别
王若凡,王浩东,石连栓
天津职业技术师范大学 信息技术工程学院,天津 300022
癫痫(EP)是一种慢性神经系统疾病,其特征是大脑神经元的阵发性异常放电[1]。根据最新流行病学数据,全球约有6 500万人受癫痫影响,近30%的患者无法通过抗惊厥药物和手术控制[2]。癫痫发作的不可预测可能会对患者的大脑造成永久性损伤,并因癫痫发作期间身体失控而造成意外伤害。脑电图(EEG)作为一种监测电生理活动的技术,已被证明是研究大脑功能的有效工具,具有无创性和高时间分辨率[3-4]。癫痫患者在发作状态下会在头皮脑电图显示振幅急剧增加与尖波、棘波或棘(或尖)慢波复合物,被认为是临床检测癫痫发作的有效手段[5-6]。然而,手工挑选癫痫脑电繁琐、耗时且存在主观因素影响[7-11]。因此,有必要寻找客观且有效的特征来自动识别癫痫,达到临床辅助诊断的目的。
近年来,将复杂网络理论、图论方法与非线性同步分析应用到多维EEG信号分析,刻画大脑神经元、神经元集群、脑区之间在各种时间-空间尺度上相互协调、相互作用,挖掘不同脑区之间的耦合关系及脑网络拓扑结构的变化规律,成为神经疾病自动诊断的研究热点[12-13]。复杂网络是一种以节点和边描述复杂系统中多个对象的相互关系,并利用图论的相关理论将网络中的复杂关系以数学公式进行量化的方法[14]。同步性是非线性科学、神经科学研究领域中的重要量化方法之一,可度量多维EEG 信号之间神经同步[15]。其中,相位同步指数(PSI)作为一种非线性量化指标,可以有效地量化信号瞬时相位之间的关系[16-17]。Cai等[18]构建PSI网络并将其应用于阿尔茨海默症检测上,发现阿尔茨海默症患者脑网络连接异常,小世界属性削弱。研究表明,基于复杂网络的脑功能网络参数(特征)相比于单通道信号特征,能更有效捕捉神经元异常阵发性异常放电的协同作用[12,19]。且多特征进行组合有助于多角度全方位展示脑电异常,提升识别效率。Pei 等[20]利用表示通道内信息和通道间信息的特征进行组合对EEG多类工作负载进行分类,结果发现相比于单特征,特征组合提高了分类准确率。Mahato等[21]将α、α1、α2、β、δ和θ功率以及θ不对称性作为特征进行组合对抑郁症患者EEG 进行识别,结果发现α2 和θ 不对称性特征的组合在SVM 中显示了最高的分类精度,达到了88.33%。Narayan[22]提取了AAR 参数、Barlow 参数、Hjorth 参数等8 个特征进行组合并作为向量输入到SVM等三类分类器进行运动脑电信号识别,研究发现,特征组合与SVM结合的方法分类精度最高,为98.8%。本课题组前期研究中,将网络拓扑特征与时频特征结合,发现特征组合可提高阿尔茨海默症的识别准确率[23-25]。因此,将特征进行组合也为癫痫脑电信号的识别提供了新思路。
特征选择通过消除或减少不相关且冗余的特征,确定最佳特征子集,即跨越类的不同属性的一组互补特征,有助于提高分类系统的性能[26]。在特征组合过程中,随着特征数量的增多,大量相关、不相关且冗余的特征会增加搜索空间,导致出现“维度灾难”[27]。而手工筛选特征,耗时、费力且无法保证准确性[28]。因此,引入粒子群优化算法进行特征子集的自动寻优,粒子群优化算法(PSO),Eberhart 和Kennedy[29]于1995 年提出,启发于鸟类群集捕食的动物社会行为,是一种基于进化方式的稳健随机启发式优化方法[30-31],具有原理和结构简单、调节参数少、搜索速度快等优点[32],常用于在多维数据集中进行特征选择。Yadva等[33]提出一种新的基于滤波器的特征选择技术,并采用PSO 算法来确定最佳特征组合,发现PSO 能有效对特征集进行降维,且提高性能。Akbari等[34]构建PSO算法与SVM分类器相结合的分类框架,对34 个空间特征进行特征筛选,可快速、准确地识别抑郁症患者EEG 信号,准确率高达99.3%。然而,PSO 算法具有一定的局限性,容易陷入局部最优,并且存在局部搜索能力差、搜索精度低等缺点[35]。而遗传算法(GA)通过选择、交叉、变异三大操作算子可以增加种群的多样性,扩大解搜索空间,可避免陷入局部最优[36],但因过度依赖这三个算子使得GA 算法整体粒子群收敛速度减慢[37]。因此,在PSO算法基础上引入GA算法,可进一步提升算法性能,实现快速收敛和种群高度多样性[38-39]。
综上,本文基于复杂网络理论和PSI算法,在delta、theta、alpha、beta 四个子频带下构建癫痫患者大脑功能网络,提取多重网络拓扑特征,并进行支持向量机(SVM)分类分析;基于进化算法的优势,采用GA-PSO 算法作为特征选择技术,将其应用于癫痫脑电网络特征的选取上,实现对单频带以及交叉频带下特征组合的优化与筛选,寻找最优特征组合,提高癫痫患者EEG信号识别的分类准确率。
1 实验设计与脑电图采集
1.1 实验数据采集对象
实验分为EP患者组和正常对照组两组,其中EP病人37例,正常人33例,均来自河北省唐山市工人医院神经内科。患者病例均为EP 大发作,具体症状表现为右侧顶中后颞持续大量中高幅尖波尖慢。此外,本实验中所有被试在实验前均已被告知完整的实验流程,确保本人自愿参加实验的情况下,由其本人或法律代表签署了知情同意书。
1.2 脑电图采集与预处理
实验使用19 通道脑电图监测系统(采样频率为256 Hz,硬件滤波器的滤波范围为0.5~100 Hz)进行EEG 记录和采集,连续持续10 min。数据分析前,从每位被试的EEG 信号中截取发作时长为8 s 的数据(数据长度为256×8=2 048个采样点),正常人和癫痫患者FP2通道脑电数据如图1所示。采用0~30 Hz的有限冲击响应(finite impulse response,FIR)带通滤波器分别对每段数据进行预处理,通过小波变换将EEG 信号分解为四个子频带:delta(0~4 Hz,δ)、theta(4~8 Hz,θ)、alpha(8~15 Hz,α)、beta(15~30 Hz,β)。
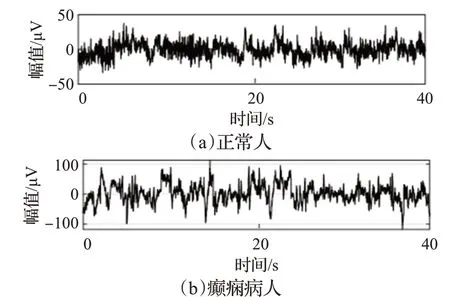
图1 正常人和EP患者EEG信号(FP2通道)Fig.1 EEG signals of normal subjects and epileptic patients(channel FP2)
2 方法
2.1 PSI网络构建
相位同步方法可用于分析大脑皮层不同区域之间的信息交互机制,通常使用相位同步指数(PSI)来量化EEG 通道间的瞬时相位同步性,以此构建EP 组和对照组的大脑功能网络。
原始各通道EEG数据设为实值信号x(t),对所有通道的脑电信号进行希尔伯特变换,记为(t):
其中,p·v表示用柯西主值定义变换。
瞬时振幅A(t)和瞬时相位φ(t)可由以下公式计算:
定义信号X和Y之间的相位差为:
其中,fm和fn分别是信号X和Y的中心频率,且m和n是满足条件m·fn=n·fm的整数。当存在fm和fn且fm=fn的频带内耦合时,设置m=n=1,并计算此时的相位差。则PSI可以定义为:
相位同步指数定义了两列脑电通道之间的相位变化。PSI取值范围在[0,1]之间,数值越大则表示两列信号之间的相位差波动越小,表明两通道信号之间同步性越强[40]。
2.2 复杂网络拓扑特征提取
“节点”和“边”是构成图的两个重要概念。基于图论的方法将每一个脑电通道作为“节点”,将通道与通道之间的PSI作为“边”,从而构建脑网络,进而进行复杂脑网络分析。复杂脑网络分析中最常用的度量包括两类,其中一类是针对节点与边属性的;另一类是针对网络总体结构和功能属性的,主要衡量网络的小世界属性。本文依据参考文献[41-43],提取15个网络特征,详细含义如表1所示。其中,前7个特征为节点和边特征,描述网络的节点紧密度与连接强度等特性,后8个为结构和功能特征,刻画网络的整体结构层次和复杂程度。

表1 网络特征含义Table 1 Explanation of network features
2.3 统计分析
单因素方差分析(one-way ANOVA)是在保证其余因素保持不变的前提下,通过单因素实验数据分析单因素A 对其观察是否存在显著影响。设原假设H0:u1=u2=…=ui,其中H1:u1,u2,…,ui不全相等,如果H0成立,说明因素A 的i个平均值相同,则称因素A 差异不显著,反之,如H1成立则称因素A 差异显著[44]。采用ANOVA 对EP 组与对照组的脑网络拓扑特征进行统计分析,研究组间差异。一般情况下,ANOVA 返回值P<0.05 表明EP组与对照组之间存在差异,而P<0.01则表明存在显著性差异。
2.4 智能算法仿真
由于不同的网络拓扑特征物理含义有所不同,并且互相之间存在一定联系[45]。此外,同一特征在不同子频带下的表现各不相同,频带之间存在耦合[46]。因此,考虑将多重网络特征进行组合,探究不同特征组合在单频带以及交叉频带下的信息交互,将组合的特征向量输入到SVM分类模型进行EP组与正常对照组的分类分析,其中SVM 类型为C-SVC,核函数为径向基(radial basis function,RBF)。
然而,当进行频带交叉组合时,四个频带(每个频带15个特征,共计4×15=60个特征)可能产生260种特征组合,人工无法高效完成特征筛选和组合。因此,引入PSO以及改进的结合算法GA-PSO,自动筛选并优化脑网络的最优特征组合,从而提高EP 组和正常组的分类精度。其中GA-PSO 算法流程图如图2 所示,具体算法流程如下:

图2 GA-PSO算法流程图Fig.2 Flowchart of GA-PSO
首先,将特征进行顺序排列,按照delta(δ)、theta(θ)、alpha(α)、beta(β)频带由低频到高频的顺序排布,每个子频带下,15特征按照表1的顺序进行排布,第1个是DG 特征,第15 个代表GIC 特征。在文献[29-34]中,粒子群大小设置30至几百不等,其中,种群很小时容易陷入局部最优,但是当种群数目增长到一定数值时,算法的寻优性能将不再提升,优化结果达到收敛。因此根据本文260种特征组合,初始粒子群大小设置为100,在SVM分类器里每个粒子个体由长度为15~60位(单频带15位,双频带30位,三频带45位,四频带60位)的0-1位点组成,其中1表示该特征被选中,0表示该特征未被选中。例如,单频带下的特征组合用粒子[010010000000100(δ)]表示选取择delta 频带的第2 个(NB)、第5 个(EB)以及第13个(HR)特征进行组合。
接下来,将选取的初始特征输入到GA-PSO算法中,设置算法总迭代次数为100。Manasrah 等[47]在GA-PSO算法前50%迭代使用GA,而后50%迭代使用PSO,证实该结合方法可以增加先通过GA算法增加种群多样性,而后通过PSO达到快速收敛寻找最优粒子,在复杂以及多维度问题具有良好的优化能力。因此,本文在解决脑网络特征组合寻优问题上,采用GA和PSO各占50%迭代的GA-PSO 算法,即各迭代优化50 次。第一阶段中,GA通过选择、交叉和变异三大操作算子传递粒子个体,进行种群更新。本文中选择算子通过轮盘赌选择和精英保留策略从一组个体中选择出最佳的个体;交叉算子通过单点交叉改变每两条染色体(粒子个体)内基因的位置来产生新的个体,交叉率0.8;变异算子是使交叉算子生成的新个体且具有比现有个体更好的适应度值,变异率为0.01。通过GA 迭代优化,可以提高粒子群的多样性,避免算法在寻优过程中陷入局部最优。第二阶段中,PSO算法第一次迭代时的初始个体即为第50次GA优化后的粒子输出。而后在每次PSO迭代中,个体的速度和位置基于全局最优位置gBest和粒子个体最优位置pBest进行更新,更新公式如下:
3 结果
3.1 脑网络特征提取与分析
首先,通过PSI算法在四个子频带下构建脑功能网络,并计算其平均网络连接,如图3 所示。结果发现与对照组相比,EP患者组在δ、θ和β频带下的网络连接更加稠密,表明EP是一种大脑异常放电的疾病。

图3 四个子频带下正常对照组与EP组脑网络Fig.3 Brain network of normal control and EP groups in four frequency bands
接下来,在四个子频带下,分别提取EP组和正常对照组脑网络的拓扑特征,分别是:度(DG)、介数(NB)、聚类系数(CC)、最短路径长度(SPL)、边介数(EB)、全局效率(GE)、局部效率(LE)、传递性(TS)、同配性(AT)、小世界系数(SW)、模块度(MD)、模体Z 分数(MZ)、层级系数(HR)、网络熵(NE)、图指数复杂度(GIC),并采用单因素方差分析(one-way ANOVA)研究EP组与正常对照组的脑网络特征差异性,结果如图4所示,其中图4(a)表示的是网络节点与边特征,图4(b)表示的是结构和功能特征。当ANOVA的返回值P<0.05时用“*”表示,而P<0.01 时用“**”表示,详细ANOVA结果的P 值如表2 所示,其中图和表中的特征都用英文缩写表示。为方便在图里统一展示,将计算结果归一化处理,因此所有特征值均在(0,1)之间。

表2 ANOVA结果(P值)Table 2 ANOVA results(P-value)
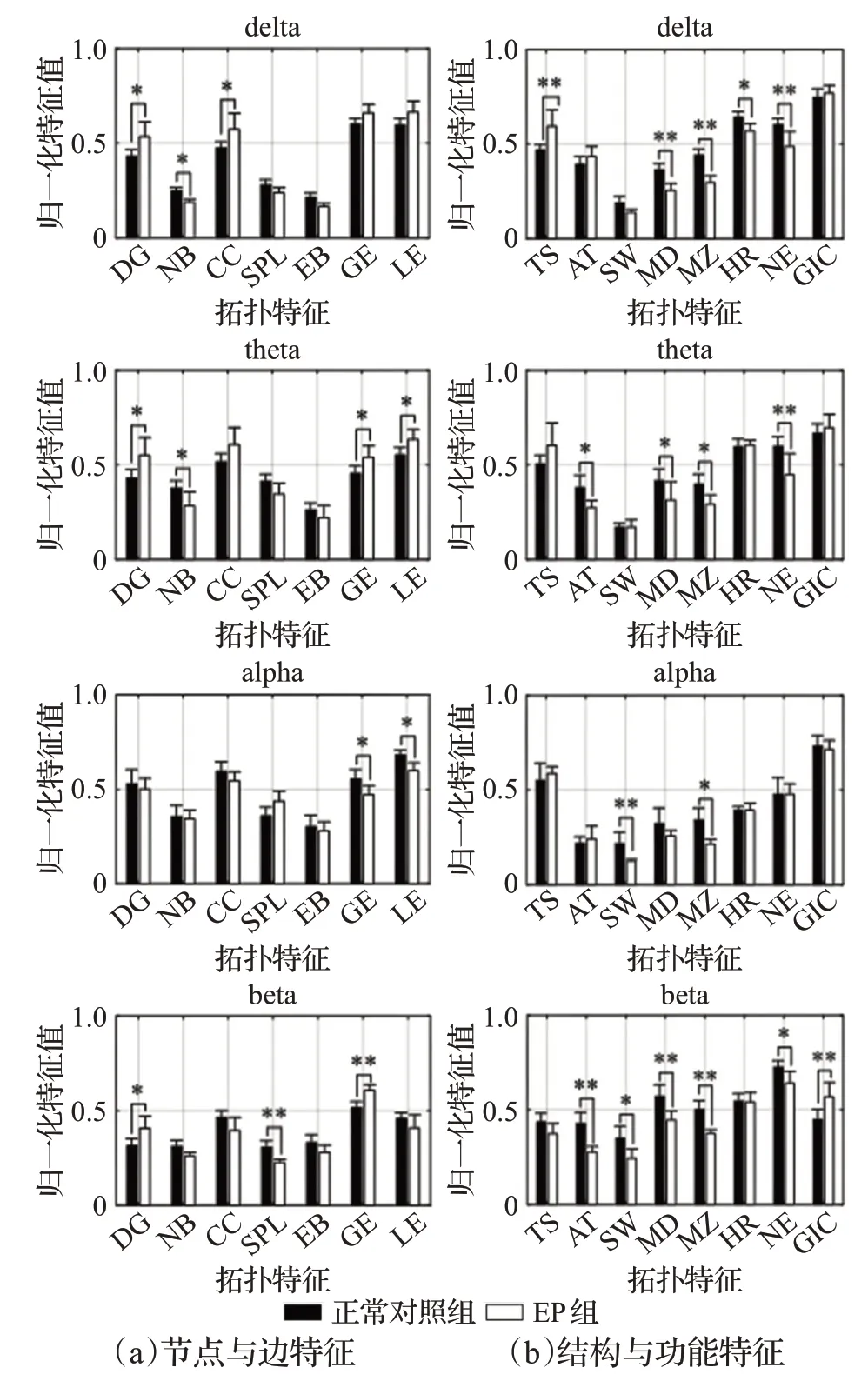
图4 特征可视化Fig.4 Feature visualization
首先,在δ频带下,由图4(a)和表2可知,EP组合与对照组的DG、NB和CC特征存在差异,相比对照组,EP组脑网络的DG、CC、GE 和LE 特征升高,表明δ 频带下的EP脑网络节点更紧密,网络传递所消耗的能量更高;而EP组脑网络的NB、SPL和EB特征降低,表明其脑网络虽然密集,但是hub节点变少且节点之间传输效率降低。从图4(b)和表2可知,HR、TS、MD、MZ和NE特征存在组间差异,其中后四个差异显著。相比对照组,EP组脑网络的TS、AT 和GIC 特征升高,表明EP 脑网络的复杂性变高;而SW、MD、MZ、HR和NE特征却降低,表明EP脑网络小世界属性和层次结构降低且更混乱。其次,在θ 频带下,由图4(a)可知,EP 组与对照组的DG、NB、GE 和LE 特征存在组间差异,其值变化呈现与δ 频带一致的结果。从图4(b)可知,AT、MD、MZ、NE 特征存在组间差异,其中最后一个差异显著。相比对照组,EP 组脑网络的TS 和GIC 特征升高;而AT、MD、MZ 和NE 特征降低。EP 脑网络的变化趋势与δ 频带基本一致。再次,在α频带下,由图4(a)可知,EP组与对照组的GE和LE特征存在组间差异,且DG、CC、SPL、GE和LE特征值变化呈现与δ和θ频带相反的结果,表明EP脑网络更稀疏且信息传递效率降低;从图4(b)可知,MZ 和SW特征存在组间差异,其中后者差异显著,除了HR和GIC 特征,其他结构与功能特征值变化呈现与δ 频带一致的结果。最后,在β频带下,由图4(a)可知,EP组与对照组的DG、SPL 和GE 特征存在组间差异,其中后两个差异显著,DG、NB、SPL、EB和GE特征值变化呈现与δ、θ频带一致的结果,而CC和LE特征值的降低表明EP网络局部聚集性降低;从图4(b)可知,SW、NE、AT、MD、MZ 和GIC 特征存在组间差异,其中后四个差异显著。相比对照组,EP组脑网络仅GIC特征升高,其他结构与功能特征降低,而TS值的降低表明EP网络信息传递能力降低。
整体来看,δ、θ和β频带较好,在这三个频带下大部分特征存在组间差异,例如DG、MD、MZ、NE特征,其中EP组的DG特征值比对照组高,后三个特征值比对照组低。此外,GE与GIC虽然仅在β频带存在显著性差异,但与DG 特征呈现相同的趋势,都是EP组高于正常组。在四个频带下,NB、EB、SW、MD、MZ、NE 特征均呈现出EP组值低于对照组,DG、SPL、GE、GIC在α频带呈现出与其他频带相反的趋势。以上结果表明,EP 在不同特征与子频带上的表现各不相同,因此,应充分考虑特征与频带这两个因素对EP脑电信号识别效果的影响。
3.2 单频带单特征分类结果
为了进一步研究EP组和正常对照组EEG信号的特征差异,采用SVM 进行分类分析。每组实验均对训练数据采用10折交叉验证,训练集和测试集的比例是8∶2。为避免偶然性,实验重复100次,分类结果以100次平均值表示,如表3所示。在四个子频带下平均准确率最高可达0.656、0.703 5、0.646 4 和0.611 2,分别对应的特征是GIC、EB、DG和MZ。此外,四个频带分别有4、5、9、9个特征的分类准确率小于0.5,无法有效区分EP组和对照组。可见,在四个子频带下,特征的分类表现各不相同,且大部分特征不具备区分功能。因此,将特征进行组合分析,聚合特征优势显得尤为重要。
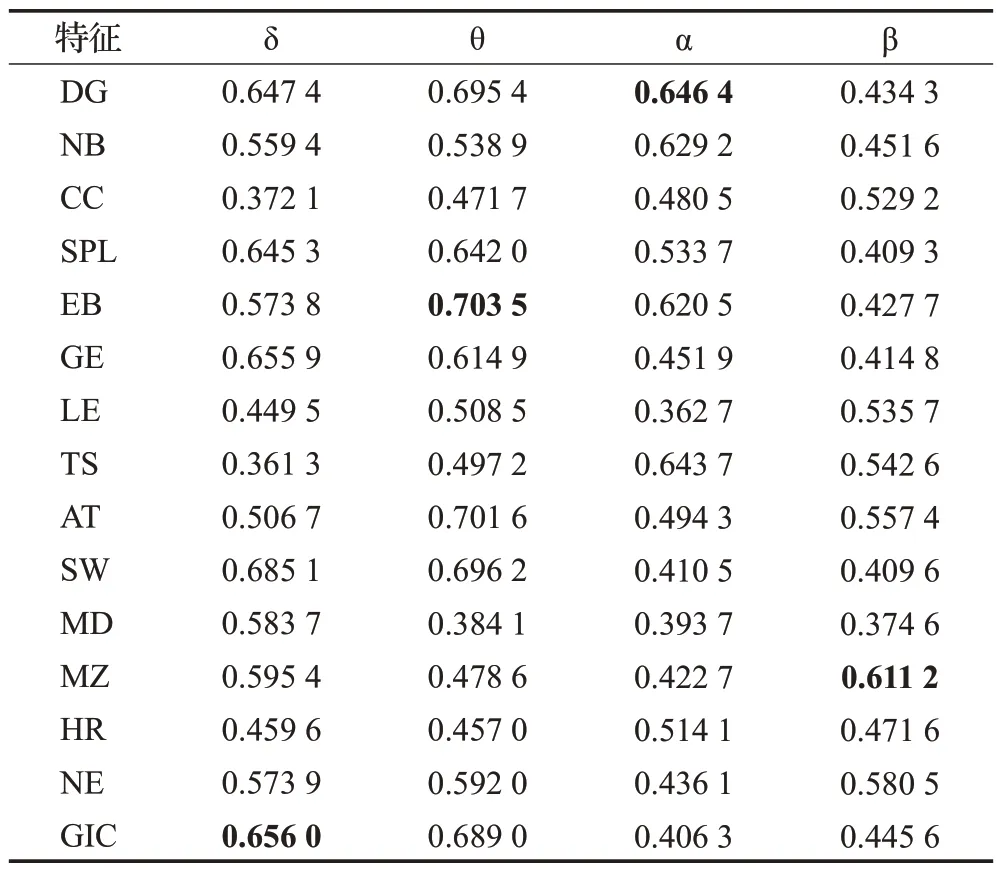
表3 四个子频带下特征的平均分类准确率Table 3 Average classification accuracy of features in four frequency bands
3.3 PSO、GA-PSO算法仿真结果
3.3.1 算法测试
为了验证GA-PSO算法避免陷入局部最优的能力,采用Ackley 和Rosenbrock 函数进行测试,其中Ackley主要用以测试算法的收敛率,Rosenbrock主要用于评价优化算法的寻优精度[48]。为避免偶然性,实验进行100次,并以100 次结果中gBest适应度值的变化为主要研究对象,其结果如图5 所示,绿色线表示GA 算法,蓝色线表示PSO 算法,红色线表示GA-PSO 算法,所有测试函数均以最小值为最优值,因此值越低优化能力越好。由图5(a)可知,GA 和GA-PSO 算法均能快速收敛找到最优值,优于普通PSO。而在图5(b)中,GA-PSO 算法的寻优精度高于GA 和PSO 算法。以上结果说明GAPSO算法比GA和PSO算法收敛速度快、寻优精度高。
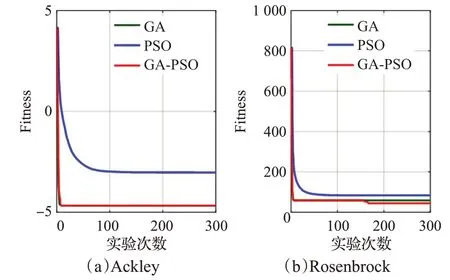
图5 算法测试Fig.5 Algorithm test
3.3.2 单频带特征组合分类结果
本小节首先采用PSO 和GA-PSO 两种算法对单频带下的15 个特征结合产生的特征组合进行筛选,实验仿真进行100次。最低分类准确率、最高分类准确率以及平均分类准确率如表4所示。100次中最高准确率所对应的特征组合如表5所示。由结果发现,在PSO算法中,四个子频带下特征组合的平均分类准确率最高出现在α频带,为0.764 9;最低出现在β频带,为0.703 9。在GA-PSO算法中,四个子频带下特征组合的平均分类准确率最高出现在δ 频带,为0.768 0;最低出现在β 频带,为0.704 8。可以发现四个子频带下的特征组合分类准确率均高于单特征,且GA-PSO 在δ、θ、β 频带下特征组合的平均分类准确率优于PSO。此外,PSO 和GA-PSO两种算法筛选的最高分类准确率都呈现δ频带>α频带>θ频带>β频带。两种算法在δ频带对应的特征组合分别为[GE-MD-MZ-NE]、[SPL-MZ-NE-GIC],其中GE、SPL、GIC 特征没有组间差异(图4 和表2),而将特征进行组合后,分类性能提高。
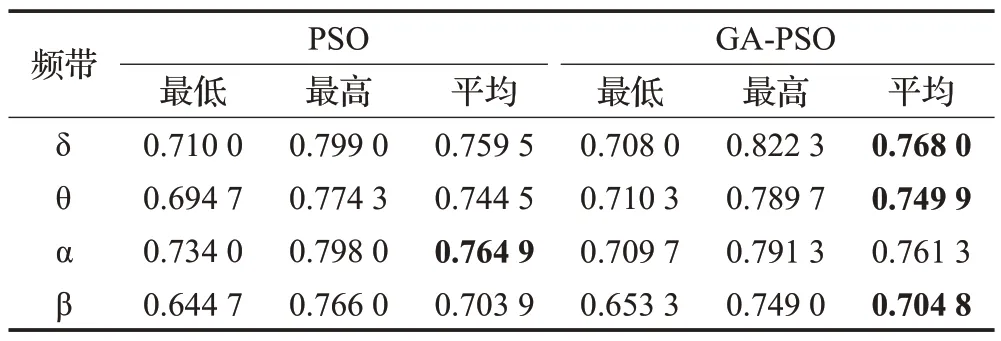
表4 单频带下PSO和GA-PSO算法寻优结果Table 4 Optimization results of PSO and GA-PSO in single frequency band
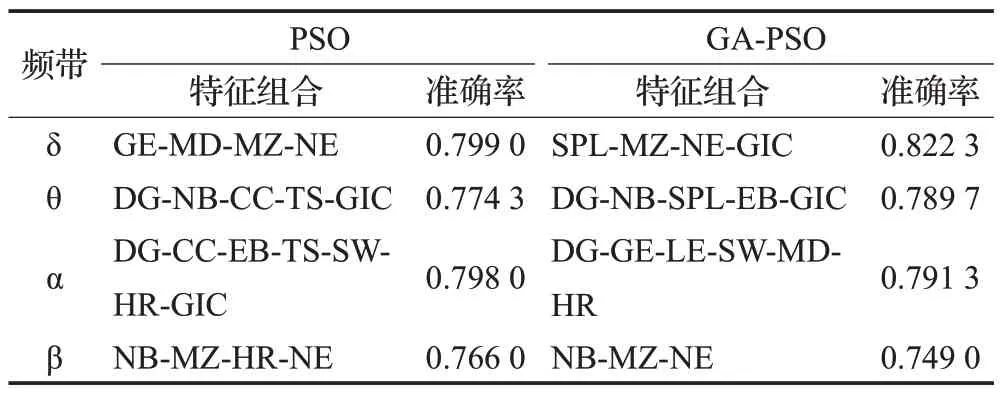
表5 单频带下最优特征组合Table 5 Optimal feature combination in single frequency band
3.3.3 交叉频带特征组合分类结果
由上述结果可知,相同特征在不同频带下的分类准确率不同,并且不同频带下的最高分类准确率也不相同,因此,应用PSO 和GA-PSO 算法筛选最优特征组合来进一步分析交叉频带组合下不同特征的组合对分类准确率的影响。实验仿真进行100 次,最低分类准确率、最高分类准确率以及平均分类准确率如表6 所示,其中双频带组合有δ-θ、δ-α、δ-β、θ-α、θ-β 和α-β 六种,三频带组合有δ-θ-α、δ-θ-β、δ-α-β、θ-α-β 四种,四频带组合仅有δ-θ-α-β一种。单频带与交叉频带下最高准确率对应的ROC曲线如图6所示,横轴是假阳率(false positive rate,FPR),纵轴是真阳率(true positive rate,TPR)。
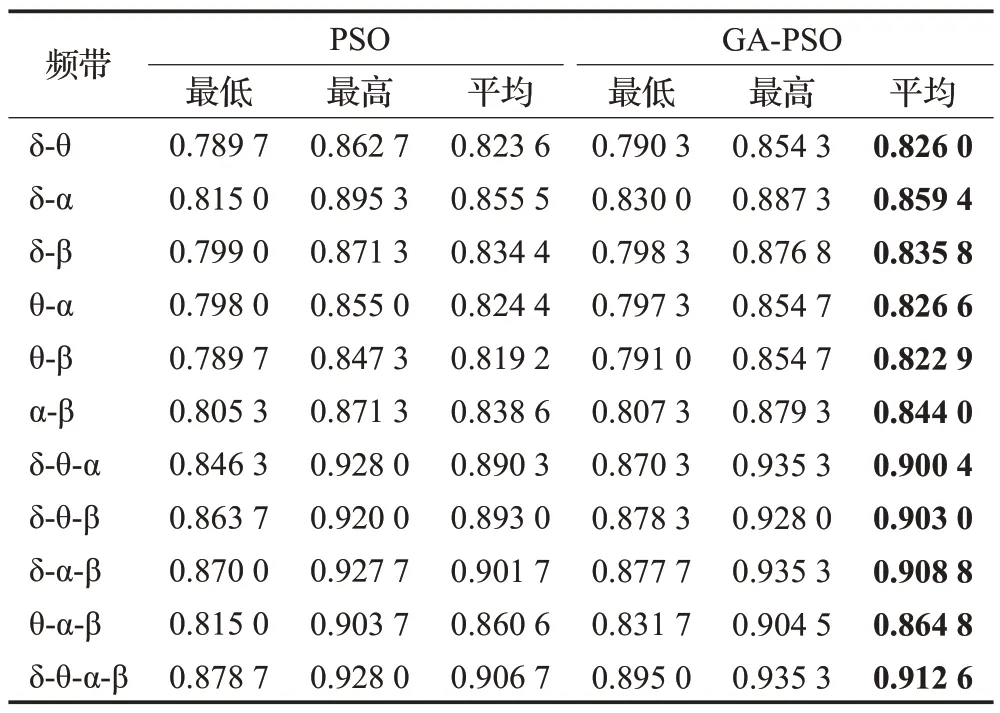
表6 交叉频带组合下算法寻优结果Table 6 Algorithm optimization results of cross-band combination
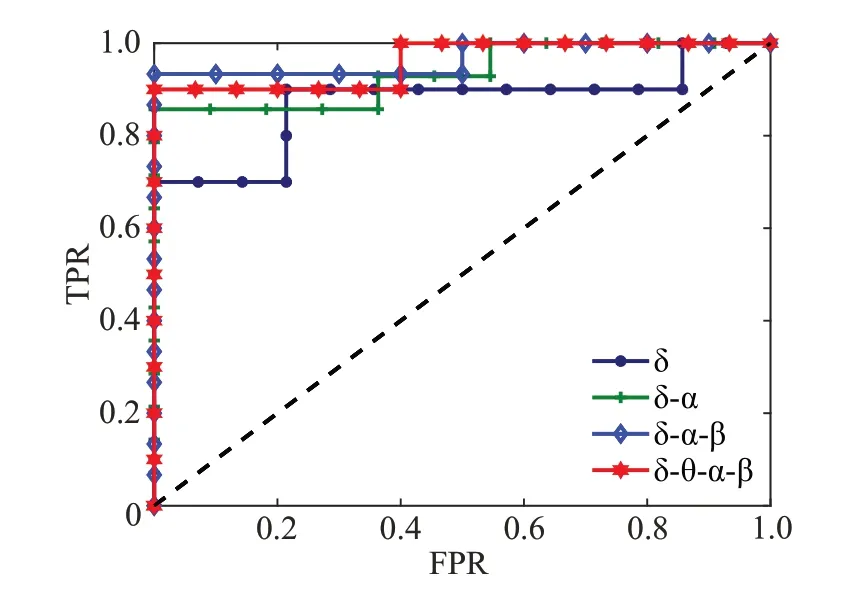
图6 单/多频带最优特征组合的ROC曲线分布Fig.6 ROC curve distribution of optimal feature combinationin single/multi-band
由表6 可知,PSO 和GA-PSO 算法筛选出的特征组合平均准确率都已超过0.81,可有效区分EP 组和正常对照组,且在任意的交叉频带下GA-PSO算法得到的平均准确率均高于PSO算法,这是因为GA的引入可提高种群的多样性,增加算法寻优的可能性,能在维度更高更复杂的解空间寻优。此外,不同交叉频带下的分类准确率不同。在GA-PSO算法中,双频带交叉得到的平均分类准确率区间为[0.822 9,0.859 4],三频带为[0.864 8,0.908 8],四频带交叉为0.912 6,可知交叉频带数目越多,分类准确率越高。此外,由表4 可知,单频带下δ 频带的特征组合准确率最高,由表6 发现,双频带至四频带交叉下δ-α、δ-α-β、δ-θ-α-β获得最高分类准确率,可知δ频带和α频带贡献度最高。
3.3.4 PSO和GA-PSO算法的寻优效果对比
为了进一步对比研究PSO 和GA-PSO 算法的寻优能力,接下来分析了将gBest(最优特征组合)作为SVM分类器输入而得到的分类准确率随迭代次数的变化规律。图7 为单频带(δ)和交叉频带(δ-α、δ-α-β、δ-θ-α-β)的结果,横坐标为迭代次数,纵坐标为100 次实验的SVM平均分类准确率。
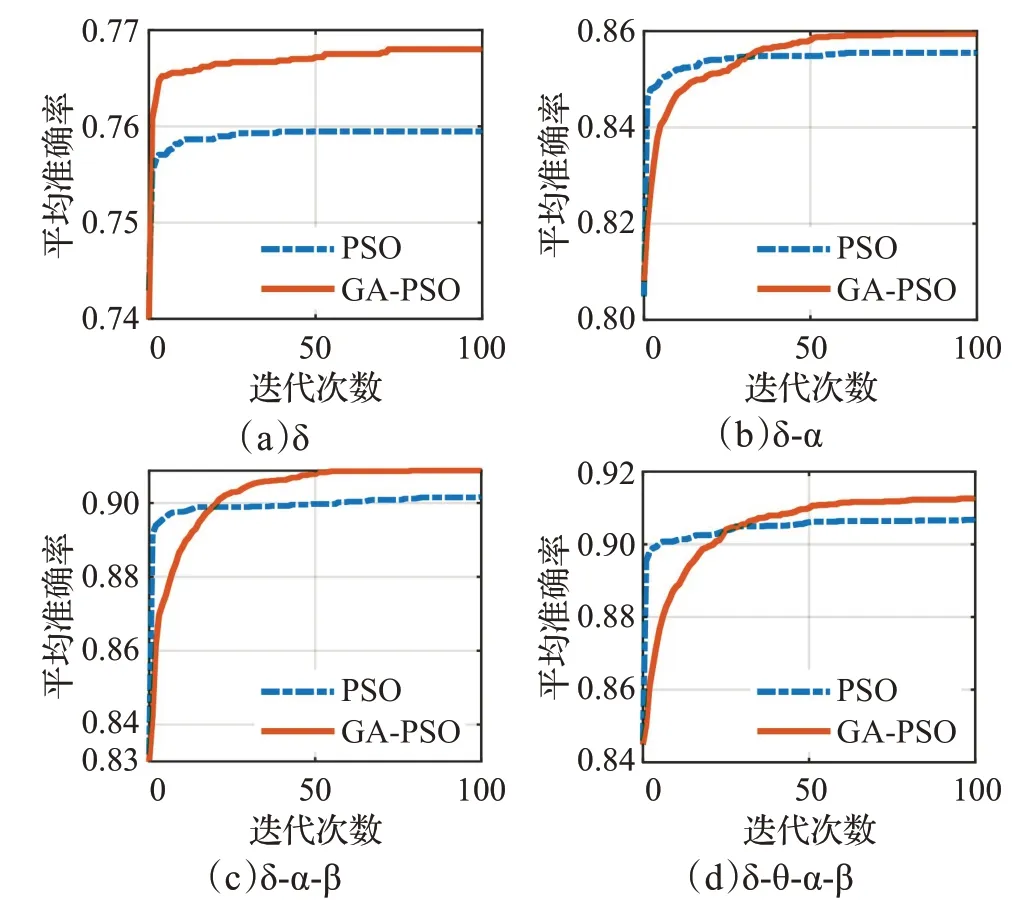
图7 PSO和GA-PSO最优粒子准确率变化趋势FIG.7 Optimal particle accuracy change trend of PSO and GA-PSO
随着迭代次数增加,PSO和GA-PSO算法筛选得到的最优特征组合的平均准确率呈上升趋势,表明两种算法都能寻找并接近最优值。然而,PSO收敛快速且收敛后曲线较平缓,在图7(a)至(d)中,单频带和交叉频带下得到的平均准确率趋向于0.759 5、0.855 4、0.901 6、0.906 7。此外,图7(a)结果与图5 一致,但是图7(b)至(d)中,GA-PSO收敛速度减慢,尤其随着交叉频带的增多收敛曲线的转折点出现得更晚,但最终趋于平缓,在单频带和交叉频带下分别得到的准确率为0.768、0.859 4、0.908 8、0.912 6,可知GA-PSO在高维解空间能得到更高的全局最优值,准确率更高。
接下来,将100 次实验中单频带到四频带PSO 和GA-PSO寻优的特征组合进行统计并均值化进行展示,如图8所示。PSO算法在单频带、双频带、三频带、四频带下寻优找到的平均特征组合数为688、2 708、3 528、4 225;GA-PSO 算法在单频带、双频带、三频带、四频带下寻优找到的平均特征组合数为2 644、5 136、5 886、6 346。对比发现,GA-PSO算法平均寻找的特征组合比PSO算法多,这表明GA-PSO由于GA的引入,通过变异操作持续增加新粒子,能扩大解空间搜索范围并寻找到准确率最高的特征组合。

图8 PSO和GA-PSO平均寻优解数量Fig.8 Average number of optimal solutions of PSO and GA-PSO
最后,为了研究PSO 和GA-PSO 算法的运行效率,将算法每次实验的运行时间进行统计,并求取均值,如表7 所示。其中,PSO 算法为:271.39 s(单频带)、380.33 s(双频带)、427.06 s(三频带)、479.46 s(四频带);而GA-PSO 算法为:137.58 s(单频带)、195.64 s(双频带)、228.78 s(三频带)、267.53 s(四频带)。从结果可知,GA-PSO算法整体上都要快于PSO算法,根据公式(6)可知PSO算法的每个粒子在进行位置和速度更新时,共进行了3 次“+”、2 次“-”和4 次“×”,以及1 次适应度计算,同时伴随着pBest和gBest更新,而GA算法每个染色体(粒子)在进行更新迭代时,交叉和变异算子仅是0-1值变换,运算量远小于PSO算法。因此,GA-PSO算法的运行效率会远高于PSO 算法,可快速、稳定寻找到最优组合。

表7 PSO和GA-PSO平均运行时间Fig.7 Average of running time of PSO and GA-PSO 单位:s
4 结语
本文基于复杂网络理论,采用相位同步指数(PSI)构建大脑功能网络并提取拓扑特征,以此识别癫痫(EP)患者发作时脑电信号。结果发现,δ、θ 和β 频带下EP脑网络连接显著增加,但hub节点变少且节点之间传输效率降低,并且网络小世界属性、局部聚集性和层次结构降低以及网络更无序。其中δ频带和β频带下的特征组间差异明显。通过SVM 分类分析发现,单频带下单特征分类准确率较低,无法有效区分EP 脑电信号。在此基础上,进行频带内和频带间特征组合,并应用PSO 算法和GA-PSO 算法寻找最优特征组合。结果发现,两种算法获得的平均准确随交叉频带的增多而升高,且最高分别为0.906 7和0.912 6。由此可见GA-PSO可获得更高的准确率,可有效识别EP 患者脑电信号。本文研究结果表明,拓扑特征能够有效表征癫痫患者的脑网络结构的异常,并通过组合的方式提高分类准确率,这为癫痫的病理研究和临床诊断提供了帮助。在后续的研究工作中,可进一步优化GA和PSO算法的结合方式,提高算法避免陷入局部最优的能力以及降低算法时间复杂度。

