基于深度学习理论的物理课堂教学实践研究
岳腊生
(首都师范大学附属中学)
党的二十大报告明确指出:要全面提高人才培养质量,着力造就拔尖创新人才.而拔尖创新人才的培养绝不能离开基础教育这个重要环节.这一过程需要彰显学生“优势发展”的教育哲学原则,遵循知识整体性学习的教育规律,超越学习成果质量标准评价的束缚,根植于丰富学生就读经历的质量内涵式发展的战略路径.就目前来讲,课堂教学无疑还是教育行为实施的主战场.
作为中学物理教师,应认真学习课程改革相关文件,深入研究学生学习方式的转变、学生主体作用的发挥、评价改革等问题,从深度学习理论的角度摸索开展拔尖创新人才培养模式.但是,教学行为的实施面临着内容多、涉及面广、课时少的问题;学生背景不同、基础不同,课堂教学实施难度大;相关工具新且方法活,教到什么程度确实是问题和挑战.面对“怎么教”的现实问题,一线教师存在彷徨、纠结、畏难等情绪,缺乏有效的课堂教学策略.
1 深度学习理论的内涵
深度学习(Deep Learning)理论于1976年由美国学者基于学生阅读实验提出,是针对孤立记忆和非批判性接受知识的浅层学习而提出的关于学习层次的一个概念.国内外研究者普遍认为:浅层学习是指被动的、机械式的、记忆性的学习,只是简单复制、机械记忆那些零散的、不相关的知识信息,不能深度理解复杂概念及其内在含义,无法主动建构个人知识体系,不能有效解决真实情境中的复杂问题;深度学习是指主动的、探究式的、理解性的学习,要求学习者主动地建构知识意义、将知识转化为技能并迁移应用到真实情境中来解决复杂问题,进而促进学习者元认知能力、问题解决能力、批判性思维、创造性思维等高阶能力与思维的发展.笔者认为,深度学习是学习者利用深度学习方法来获得高质量学习结果、实现有意义学习的一种高阶学习,综合而言,深度学习突出以学生为中心,强调引导学生主动学习,在路径上注重促进学生的新旧知识联结,强调信息整合与批判性理解,最终实现发展学生解决现实问题的能力与高阶思维的目的.
2 促进深度学习的课堂教学
随着教学改革的纵深推进,新的教学理念被教师们所接受,但在实践层面仍存在不足.从学习目标来看,教师往往在教学内容中生套核心素养,导致知识与技能目标流于浅层;学习内容方面,仍然沿袭接受记忆、强化训练的指导模式,新知识没有与原有知识建立联系,学生不能把知识迁移到新情境中去;学习方式上,将教学活动本身作为教学目的,导致自主、合作与探究变成使学生机械地记忆课本上的知识,难以递进式地促进学生创新意识、批判思维和实践能力的发展;从学习结果来看,学生的思维层次仍处于低阶水平,举一反三的迁移能力和解决实际问题的能力普遍偏弱.可以看出,一般教学模式更多为浅层学习,导致学生被动学习,仅停留在“知道和领会”知识的认知层面.
为此,有学者提出基于深度学习理论的课堂实施策略,认为深度学习需要教师通过确立高阶思维发展的教学目标,整合意义联结的学习内容,创设促进深度学习的真实情境,选择持续关注的评价方式进行积极引导.还有学者认为深度学习的课堂教学应当做好现实经验与知识的相互转化,让学生主动活动,帮助学生通过深度加工把握知识本质,模拟社会实践及引导学生对知识进行价值评价等几项工作.综合来看,以深度学习理论为指导进行教学设计可有效解决一般教学模式在学习目标、内容、方式等方面存在的问题.
通过对比浅层学习与深度学习理念差异及一般教学模式与深度学习课堂的教学策略,笔者进一步提出基于深度学习理论的物理课堂教学实践策略.下面以高中物理“运动的合成与分解”部分的教学为例,针对教材中的陈述性知识,通过创设真实的情境问题,采用问题链与思维探究相结合的教学方法,鼓励学生积极思考,在真实的问题情境中,积极参与课堂活动,达到在深度体验中获取知识、提升能力的目的.
2.1 通过创设物理情境,引导学生深入思考
作为一种具有主动性和批判性的学习方式,深度学习面向真实问题的解决,要求学习者在激活先前知识的基础上,对于所获得的新知识进行有效深度加工,因此情境创设需要突出“真实”与“知识建构”.情境创设要倾向现实生活场景,初步导出的问题应与已有经验相关,从而引导学生进入情境并逐步深入思考.
基于以上思考,本文提出问题情境:A、B、C三个芭蕾舞演员分别同时从边长为L的正三角形的三个顶点A、B、C出发,以相同的速率v0运动,运动中始终保持A朝着B,B朝着C,C朝着A.
2.2 问题链引导思维,注重知识的保持与迁移
为引导学生快速深入理解问题情境,层次递进地进行高阶思维,研究采用问题链的形式,旨在先调动学生积极性,引出学生原有知识,进而引导学习反思与批判理解.在问题链的层次递进中,学生思维层次渐深,解决问题的知识不断迁移分化,高阶能力得到发展.
问题1A、B、C三个芭蕾舞演员最终会在哪里相遇?
猜想会在等边三角形中心相遇.
问题2A、B、C三个芭蕾舞演员经过多长时间相遇? 有同学简单思考后给出了下列方法.
方法1正交分解法
将v0沿三角形的高正交分解得
相遇的时间为
上述解法属于直接按照猜想的相遇结果进行的推理,教师紧追不舍提出问题.
问题3针对刚才同学凭借直觉猜想的结果,是否能用我们目前所学知识给出严谨的解答呢? 经思考后有同学又提出了一套方案.
方法2相对速度法
由对称性,每时每刻A、B、C的位置都构成等边三角形,现从相对速度的角度考虑等边三角形边长的变化,显然当边长变为0时,三个舞蹈演员会汇聚于等边三角形中心.
如图1所示,由于瞬时速度都沿当前等边三角形的边的方向,则A相对B的速度
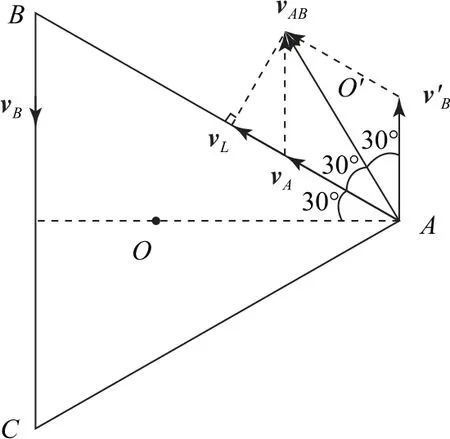
图1 A 相对B 的速度
由|vA|=v0,|vB|=v0,则由角度关系得
则边长减少速率为
则相遇所需时间
在同学们还在为能求得舞蹈演员相遇时间而兴奋时,接着提出另一具有挑战性的问题.
问题4以演员A为例,能求出她的运动轨迹方程吗?
几个具有微积分和极坐标相关知识基础的同学摩拳擦掌,跃跃欲试.不久,大家提出了以下解决方案.
方法1速度分解法
由于A、B、C三个舞蹈演员的运动关于等边三角形的中心旋转对称,每时每刻三者都构成等边三角形,这里只考虑A的运动情况即可.将A的速度分解为向中心连线OA的径向和垂直于中心连线的切向,则速度方向与中心连线的夹角θ=30°,如图2所示.

图2 A 的速度分解
则径向速度始终为
切向速度始终为
则A与中心O的连线(以下称为矢径)OA长度减小的速率即为径向速度vτ,初始矢径长度为r0,由几何关系,则可以写出矢径长度关于时间的表达式
当r=0时,三者相遇,此时
角速度为切向速率除以矢径长度
则
对于时刻t0,相对初始状态单个演员的矢径相对中心O转过的角度
则其运动的角度φ和矢径长度r关系方程为
还有同学利用所学极坐标方法给出了另一种解法.
方法2建系微元法
以等边三角形中心为极点O,初始时刻极点O到舞者A的连线为极轴OP,建立极坐标系,如图3所示.对于开始运动后的任意过程,用微元法分析其位置变化规律,设时刻t时,三者构成△ABC,极径为r,极角为θ,经过一个微元时间dt,A的位置变为A′,AA′长度La=v0dt,时刻变为t+dt,极径变为r+dr(dr<0),极角变为θ+dθ,其关系如图4所示,dθ极小,则由几何关系有
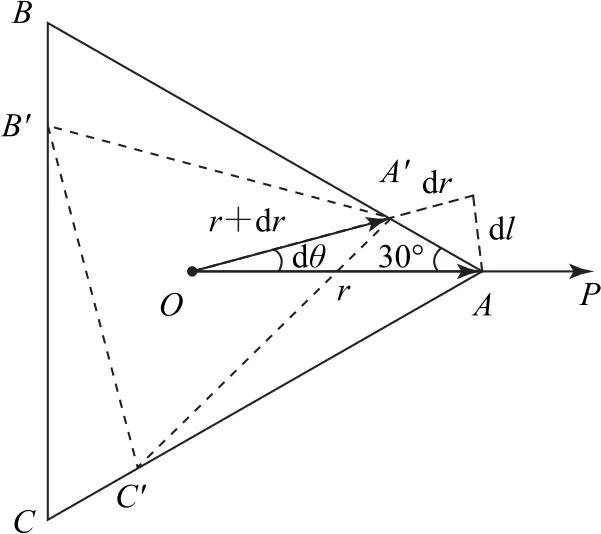
图3 建立极坐标系
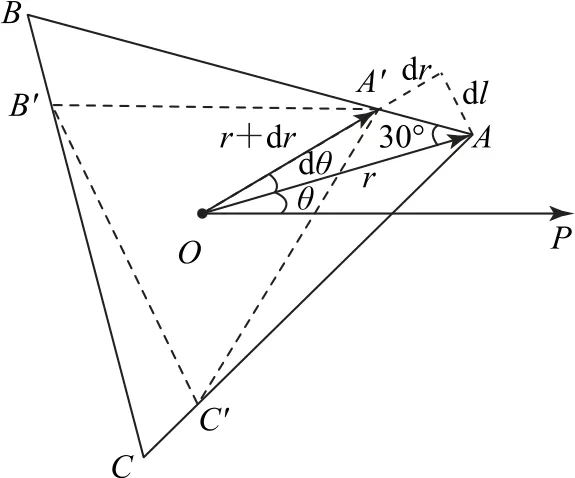
图4 位置变化图示
整理式○15得
即
整理式○16并将式○18代入得
对式○17左右积分,并代入初始条件r=r0,t=0,对于时刻t0有
即
当r=0时,三者相遇,此时
即
同学们通过不同的理论推导方法,得到了同样的结论,看上去已经得到了相互的印证,此时再适时引导学生进一步通过其他研究方法来证明.
问题5能否从其他角度验证一下同学们的解法是否正确?
此时,又有同学提出可以通过模拟绘图验证结果是否正确.利用几何画板画图软件绘出了三个舞蹈演员的运动轨迹(如图5).图片一经展示,全班同学都兴高采烈,感到收获满满! 不仅学会了一道基础的物理问题,还在交流中感受到了深度学习的魅力!
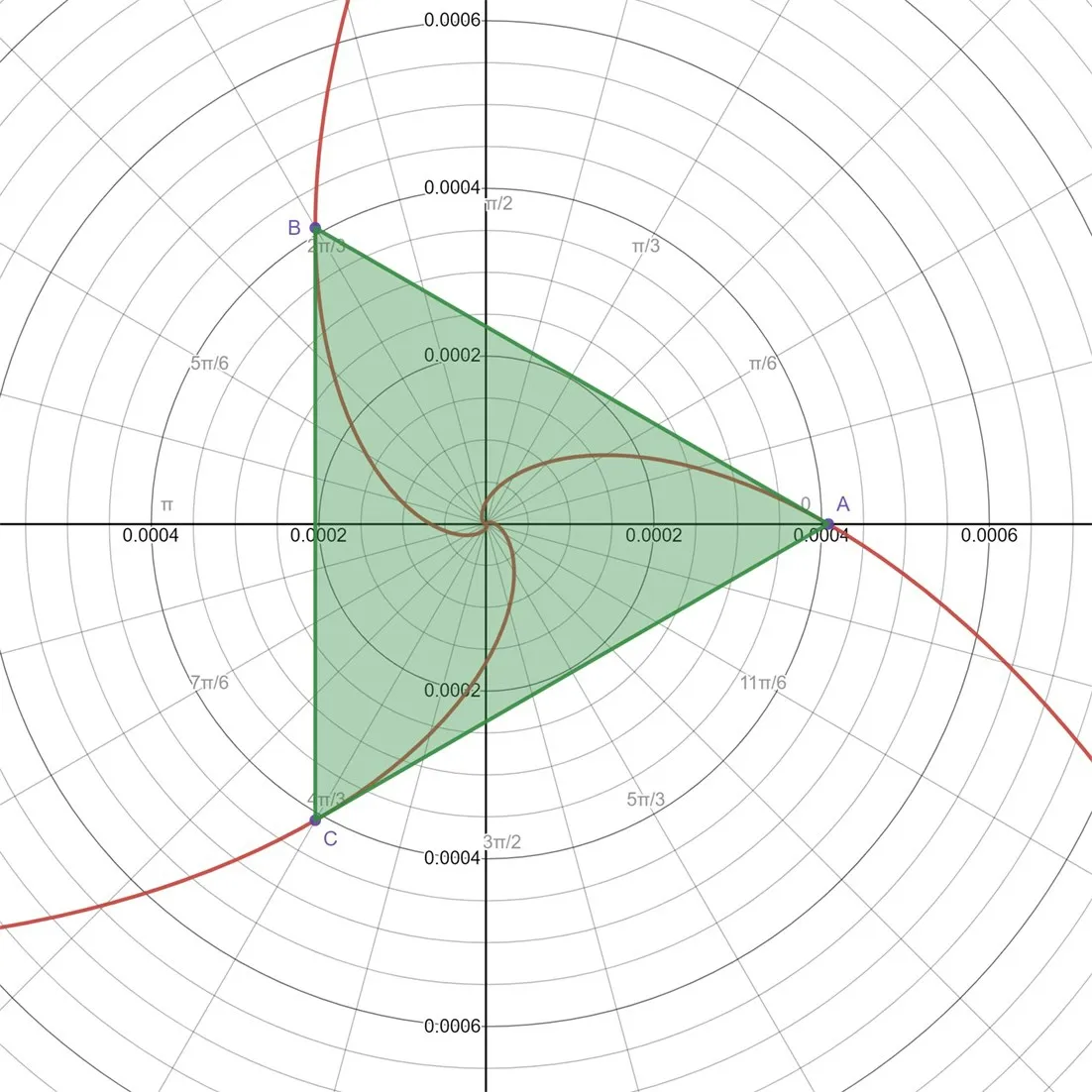
图5 利用模拟绘图验证运动轨迹
3 基于深度学习理论的物理课堂教学实践策略
3.1 突出以学生为中心
深度学习强调以学生为中心、以学习为导向,既关注学生的学习过程,也关注教师的教学活动.本节课从典型的物理情境出发,通过问题链的次第推进,探究科学的结论;通过设计教学和评价活动等来帮助学生掌握复杂的知识概念,建构个人知识意义,发展个人理解能力等.
3.2 提倡主动学习
本节课不受常规的所谓大纲、考纲甚至课时局限,从一开始就设计了学习内容“上不封顶”的“一体化”模式:从三个芭蕾舞演员的运动情境→猜测演员在中心会聚→计算会聚时间→推导轨迹方程电脑模拟验证.鼓励有能力的同学在条件许可的情况下,自学微积分初步、高等数学等知识.从“优势发展”教育原则的角度来看,在中学阶段这样的课堂教学无疑是对拔尖创新人才培养的有益尝试.也正是深度学习者具有内在的学习动机、积极的学习态度和强烈的学习兴趣的特征体现.
3.3 注重批判理解
本节课一开始,同学们还有猜测、疑惑、不坚定或拿不准等心理状态.可是随着大家在理解基础上批判性地学习,批判性地看待新知识并深入思考,逐渐加深了对深层知识和复杂概念的理解,最终达成对问题的完美解决.
3.4 强调信息整合
首先,深度学习是多渠道信息的整合,学习者不仅要接受书本内容或教师传授的知识,更要通过多种途径来获取完成学习任务所需的其他知识信息,如极坐标、微积分知识.其次,深度学习是多学科信息的整合,如在基于问题的学习过程中要应用到多门学科的知识,如电脑模拟舞蹈演员轨迹使得推理得到验证,而不是教师简单认可.再次,深度学习是新旧信息的整合,它把新信息与已知概念和原理联系起来,整合到原有的认知结构中,从而引起对新信息的深度理解、长期保持及迁移应用.
3.5 促进知识建构与转化
学习者不仅要能从信息的海洋中获取有用的信息,更要将信息转化为知识,并把新知识与已有知识经验联系起来,在已有知识结构的基础上建构新知识.本节课就是一个简单的生活问题,同学们利用所学运动的合成与分解、运动的相对性等知识,在深度学习的经历中,体会了一次从一般到复杂再到简单的思维训练过程.实际上就是通过在新的情境中迁移应用所掌握的知识技能,将一般性的知识技能转化为问题解决技能,以获得高阶能力的过程.
3.6 面向问题解决
本节课设置了问题链,环环相扣,使得学习者灵活运用所学知识来解决真实情境中的复杂问题、创造新知识.“学以致用”实现了深度学习的目的.
3.7 发展高阶思维
高阶思维是发生在较高认知水平层次上的心智活动或较高层次的认知能力,在教育目标分类中表现为分析、综合、评价、创造等较高认知水平层次的能力.浅层学习主要是对知识的简单描述、记忆或复制,停留在“知道、理解”等较低的认知水平,是一种低级认知技能的获得,涉及简单记忆、浅表理解、良构问题解决等低阶思维活动;相反,深度学习更注重知识的理解和应用,处于“应用、分析、评价、创造”等高级的认知水平,面向高级认知技能的获得,涉及劣构问题解决、元认知、批判性思维、创造性思维等高阶思维活动.高阶思维是实现深度学习的关键,发展高阶思维能力有助于实现和促进深度学习;同时高阶思维又是深度学习的核心特征,深度学习的实现有助于提高学习者的思维品质和学习效能.
4 结束语
在设计整个物理课堂教学时,绝不是简单地提出一个或几个问题形成所谓的问题链就可以了,还必须处理好诸如“游离与沉浸”“浅表与深层”“知识与智慧”的关系.这只是深度学习理论用于高中物理课堂教学的一个案例,而深度学习作为中学生学习物理行之有效的方式,值得我们更进一步地研究和实践.
(完)

