例析运动的合成与分解的3种模式
戴颖昱
(江苏省南京市秦淮中学)
运动的合成和分解是解决复杂运动问题的常用方法之一.一个物体在不同的方向同时参与几个运动时,它的实际运动是合运动,其他几个运动是分运动.
1 合运动与分运动的关系
1)独立性:一个物体同时参加两个或更多的运动时,其中的任何一个运动并不因为另一个运动的存在而有所改变,这就是运动的独立性原理.独立性原理是运动的合成与分解的理论基础.根据独立性原理可求合运动的时间.
2)同时性:合运动和分运动是同时开始、同时结束的,合成分解必须在同一时刻进行.
3)等效替代性:合运动是由各分运动共同产生的总运动效果,根据研究问题的方便,合运动和分运动可以相互替换.
4)矢量性:合运动与分运动满足平行四边形定则,即位移、速度、加速度的合成与分解都满足平行四边形定则.
2 运动合成与分解的3种模式
模式1 船过河
船的分运动之一是顺水而下,分运动之二是相对水运动.想要使过河时间最短,需船头垂直对岸过河;求解最短过河位移时要看船相对水的速度和水流速的关系,即需分情况讨论.设水流速度为vs,已知船在静水中的速度为vc,若vc>vs,则按如图1-甲所示情形过河位移最短,若vc<vs,则按如图1-乙所示情形过河位移最短.

图1
例1四人乘坐同一条船渡河时,船在静水中的速度v1和水速v2一定,渡河的最短时间为t1,用最短位移渡河的时间为t2,下列说法正确的是( ).
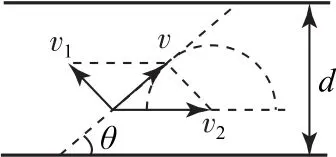
图2
模式2 船靠岸
绳子拉船靠岸属于绳子末端速度的分解问题.如图3 所示,实际运动对应了小船的合运动(可以等效为绳子末端的运动),可以将实际运动分解为两个分运动:一个运动沿着绳子收缩的方向,速度为v;另一个运动使绳子绕着定滑轮顺时针转动.实际速度可以沿着绳子缩短的方向和垂直绳子的方向分解.由数学知识得.对绳端物体速度进行分解时,常犯的错误就是将速度的分解和力的分解相混淆,从而得到v船=vcosθ的错误结果.若用能量的思想解决问题,则不易犯错误.人对绳子输入的功率P入=Fv和绳子对船的输出功率P出=Fv船cosθ相等,即可得船靠岸的速度
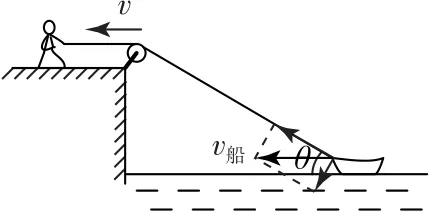
图3

图4
例2在河面上方10m 的岸上有人用长绳拴住一条小船,开始时绳与水面的夹角为30°.人以恒定的速率v=2.5m·s—1拉绳,使小船靠岸,那么( ).
A.船受到的合外力为0
B.3s时绳与水面的夹角为60°
C.3s时小船的速率为3.75m·s—1
D.3s时小船距离岸边7.5m
模式3 射击问题
射击时,不论是靶动还是枪动,要想击中靶,瞄准时应保证子弹相对靶的速度沿二者的连线方向.
例3在民族运动会上有一个骑射项目,运动员骑在奔驰的骏马上,弯弓放箭射击侧向的固定目标,若运动员骑马奔驰的速度为v1,运动员静止时射出的弓箭速度为v2,直线跑道离固定目标的最近距离为d,要想在最短的时间内射中目标,则运动员放箭处离目标的距离应该为( ).
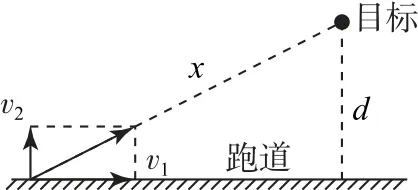
图5
以上给出了3种常见的运动的合成与分解的模式,对于一个确定的运动合成与分解,我们在分析运动的基础上,可套用前文中的一种合成与分解的模式.运动的合成与分解是从等效的角度研究运动本身的,切忌把运动的合成与分解同力的合成与分解混为一谈,两者之间没有必然的联系.
(完)

