刍议斜上抛运动中的水平射程的极大值问题
张立那
(河北省石家庄市第一中学)
随着各省市地区新课程、新教材、新高考的推进实施,试题考查越发凸显了对“情境”的要求.“抛物运动”是生活中最常见的情境,而“斜抛运动”中的“射高”和“射程”的极值问题是高中物理中的重点和难点.本文将呈现此类问题的一些处理方法和技巧,以供参考.
情境1当抛出点和落地点等高时,首先在忽略空气阻力的条件下,建立斜抛运动一般模型如图1所示,其中v0为物体的抛出速度,θ为速度与水平面的夹角,g为重力加速度,采用化曲为直思想,分解速度.
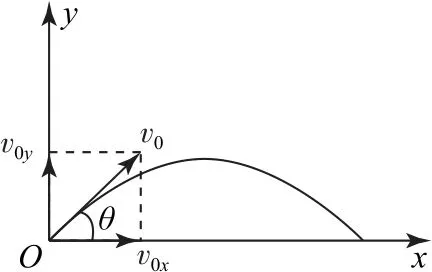
图1
水平方向的初速度v0x=v0cosθ.
竖直方向的初速度v0y=v0sinθ.
水平方向的位移方程为x=v0xt=v0tcosθ.
竖直方向的位移方程为
斜抛物体能达到的最大高度叫射高,抛出点到落地点的水平位移叫射程.
情境2当抛出点和落地点不等高时,尤其是在落点低于抛出点时,如何控制方向才会使水平射程最远呢? 射高又如何求解?
例1如图2 所示,某同学在高度h处以大小一定的速度v0抛出一小球,当其速度方向不同时,落地点与抛出点的水平距离即射程大小也不同,若不计空气阻力,则最大射程为( ).

图2
水平方向vx=v0cosα,
竖直方向vy=v0sinα.
方法2画出位移矢量合成图,如图3 所示,在直角三角形中由勾股定理有h)2,整理得
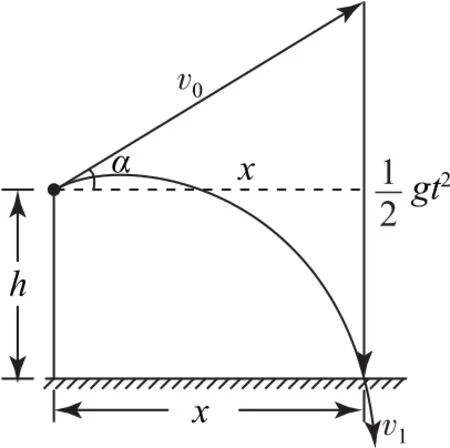
图3
后续处理方法同方法1,都是利用二次函数求极值的处理思路.
方法3画出速度及速度变化的矢量图,如图4 所示,初速度v0大小确定,速度方向未知,末速度大小为为定值,Δv为此过程速度的变化量,方向为竖直向下,则物体的水平射程
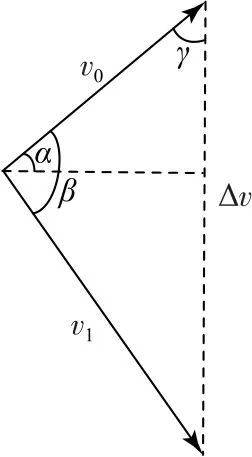
图4
拓展延伸一些电场中问题的求解处理,与上述情境如出一辙,也是“斜上抛”模型,仍然可采取化曲为直、速度矢量图等方法分析.
例2如图5所示,在匀强电场中一质量为m、电荷量为q的正粒子先后经过a、b两点,在a点的速度大小为3v,速度方向与ab连线的夹角为53°,在b点的速度大小为4v,速度方向与ab连线的夹角为37°,ab连线长度为d,sin37°=0.6,cos37°=0.8.若粒子只受电场力作用,则下列说法正确的是( ).

图5
B.场强方向与ab连线的夹角为74°
C.从a到b,粒子的运动时间为
D.从a到b,粒子的最小速度为

图6
方法2画出速度及速度变化的矢量图(如图7),虚线连接3v、4v的矢量末端,此虚线为Δv的方向,右偏下,也即场强方向,建立坐标系,设x方向与水平虚线夹角为α,则粒子在x方向做匀速运动,有粒子在a、b两点速度分量相等,即3vcos(53°—α)=4vcos(37°+α),解得α=16°,即可得出y方向或场强方向.此题其他问题求解可参考方法1.此方法十分巧妙地利用了速度变化矢量图.

图7
综上所述,抛体类极值问题对物理学科核心素养要求较高,在解决此类问题时要运用多种数学物理方法和思想,同时还要注意数形结合,加强模型建构.
(完)

