一个具有共存吸引子的四阶混沌系统动力学分析及FPGA 实现*
全旭 邱达 孙智鹏 张贵重 刘嵩
(湖北民族大学智能科学与工程学院,恩施 445000)
1 引言
混沌是一种自然界中普遍存在的物理现象,Lorenz 在研究天气预报系统时发现了该现象并提出了著名的Lorenz 混沌系统[1].学者们以此系统为基础,相继提出了Chen 系统[2]、Lü系统[3]、Bao系统[4]等,极大地促进了混沌系统的研究和发展.混沌系统因其复杂无序的性质被广泛应用于保密通信[5,6]、图像加密[7,8]、同步控制[9,10]等领域.1971年,蔡少棠[11]首次提出忆阻器的概念,Strukov 等[12]于2008 年制造出了第一个忆阻器的实物,验证了蔡少棠教授的猜想.学者们利用忆阻器优良的非线性特性,构建出了具有更加复杂动力学行为的四阶,五阶和更高阶的混沌系统,并发现了多翼混沌吸引子[13,14]、隐藏吸引子[15,16]和共存吸引子[17,18]等不同种类的吸引子.其中,共存吸引子是由不同的状态变量初值将系统引向不同的吸引子,形成多吸引子共存的多稳态现象.共存吸引子可分为对称共存吸引子和非对称共存吸引子,它使得系统运行轨迹变得不可预测,从而更适用于信息安全领域,因此对共存吸引子的研究具有重要的意义.
目前,从构建混沌系统的角度来说,构建具有共存吸引子的混沌系统主要有3 种方法.第1 种是在三维系统中加入状态反馈控制器.鲜永菊等[19]将反馈控制器引入至三维混沌系统的第3 个方程中,构建了一个只有一个平衡点的四维超混沌系统,该系统具有至少12 种吸引子共存类型.李木子等[20]提出了一个含有两个反馈项的新五维超混沌系统,该系统不存在任何平衡点,即可以产生隐藏共存吸引子.第2 种是利用忆阻器替代混沌电路中的元器件或直接引入到混沌电路.闵富红等[21]利用两个双曲函数型忆阻器分别替代蔡氏电路的蔡氏二极管和电阻,构建了一个具有多稳态特性的混沌电路.Ma 等[22]设计了一个含有两个忆阻器的混沌电路,该电路具有无穷多个平衡点,并且可产生7 种不同类型的吸引子.第3 种是将忆阻器引入到现有的混沌系统.Bao 等[23]提出了一个具有4 个线平衡点的忆阻混沌系统,该系统可表现出无穷多个吸引子共存的超级多稳态现象.Yu 等[24]将一个二次非线性磁控忆阻器作为反馈项,提出了一种具有不同类型共存吸引子的五阶混沌系统.李晓霞等[25]将一个磁控忆阻器引入到四维Lü混沌系统,构建了一个具有超级多稳定性的五维超混沌系统.秦铭宏等[26]将三次型磁控忆阻器引入三维混沌,构建了一个具有无穷多共存吸引子的新四维混沌系统,验证了系统状态变量的震荡幅度与初始值密切相关.
尽管具有共存吸引子的混沌系统已有文献报道,但呈现旋转共存吸引子的混沌系统目前研究尚少.本文结合之前学者的研究思路,在三维混沌系统的基础上引入状态反馈控制器和磁控忆阻器,构建了一个新四阶混沌系统.该系统可以产生四种类型共存吸引子,并且能够产生两种情况的旋转共存吸引子.最后基于SOPC (System-on-a-Programmable-Chip)技术建立硬件实现平台,物理实现了该系统,验证了新系统的可行性.
2 新四阶混沌系统的构建
2.1 系统模型
忆阻器是一种无源两端元器件,描述了磁通量φ和电荷q的关系,本文选取文献[27]提出的磁控忆阻器模型:
其中,φ为磁通量,u为施加在忆阻器两端的电压,i为流过忆阻器两端的电流,W(φ) 为磁通控制忆阻器的忆导函数,正实数a1,b1为忆阻内部参数.当a1=1,b1=0.02 时,对模型(1)施加正弦激励电压v(t)=Vmsin(2πt),忆阻器的磁滞回线如图1 所示.当输入电压Vm=2V时,输入频率f分别为0.01,0.02 和0.03 Hz 时忆阻器的磁滞回线见图1(a);当输入频率f=0.01V时,输入电压Vm分 别为1.5,2.0 和2.5 V 时忆阻器的磁滞回线见图1(b).

图1 忆阻器的磁滞回线Fig.1.Hysteresis loop of memristor.
Chen 等[28]提出了一个特殊的三维自治二次类Lorenz 混沌系统,该系统具有两个稳定的结焦点,其状态方程为
其中x,y,z为状态变量,a,b,c表示系统参数.当系统参数固定为a=10,b=100,c=11.2,且初始条件为 (0.98,-1.82,-0.49) 时,系统(2)可以显示一个类Lorenz 混沌吸引子.
通过在系统(2)第2 个方程的右侧添加一个反馈控制器w,同时增加磁控型忆导W(φ) 与y的乘积作为非线性项,构建了一个新的四阶混沌系统,其状态方程为
式中,x,y,z为系统状态变量,a,b,c,d,e,h为系统参数.当系统参数固定为a=6,b=41,c=1,d=0.5,e=10,h=1.1,初始值为 (2,2,0.01,0.01) 时,系统(3)呈现双涡卷混沌吸引子,如图2 所示.计算系统的4 个Lyapunov 指数分别为LE1=0.595,LE2=-0.155,LE3=-6.685和LE4=-12.240,其Kaplan-Yorke 分数维DL=3.99,显然系统(3)有1 个正的Lyapunov 指数,且4 个指数之和小于0,说明新构建的系统是混沌的.同时,发现新系统关于y轴对称,其对称性可从(x,y,z,w)→(-x,y,-z,-w)的不变性证实.
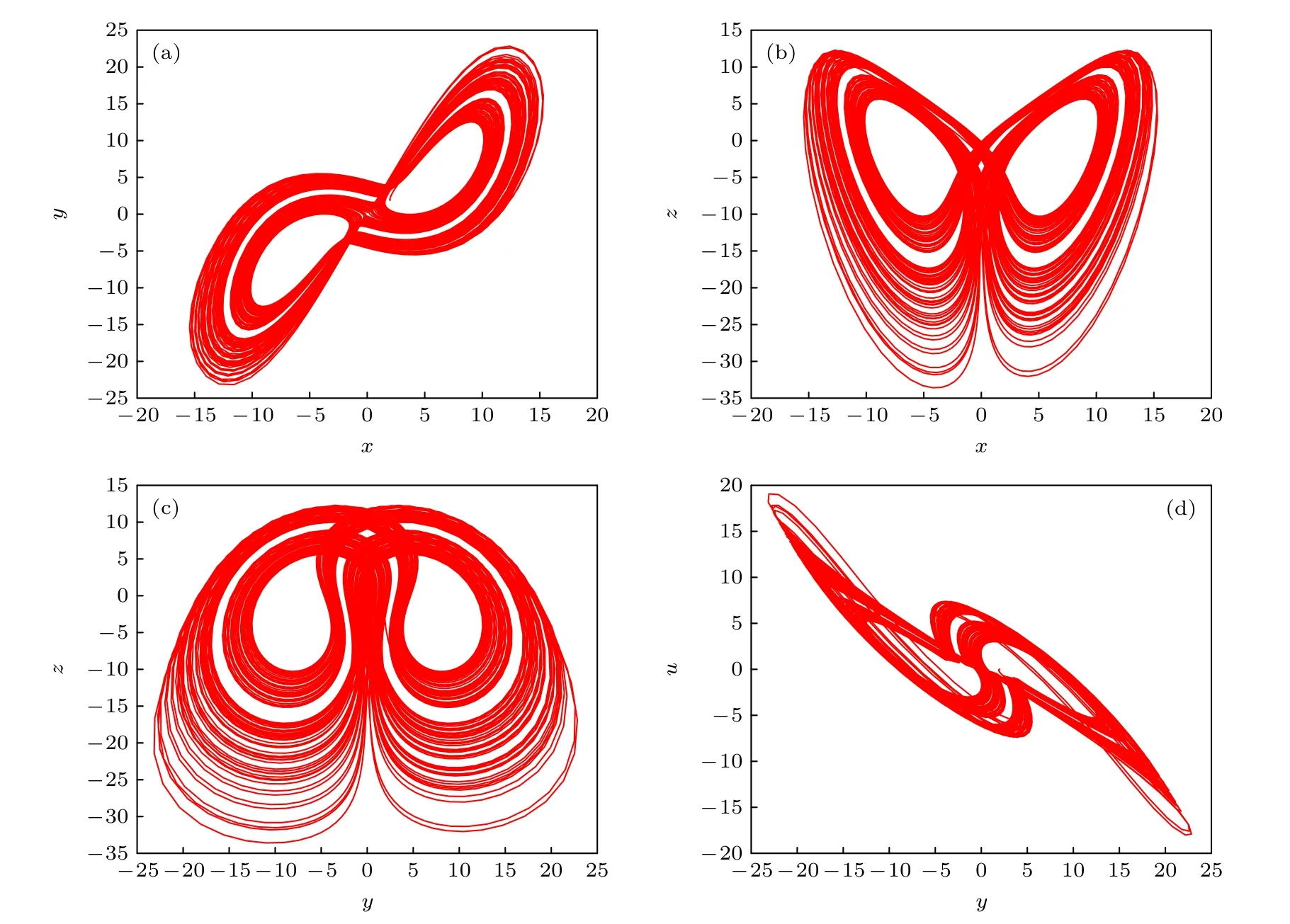
图2 混沌吸引子各平面相图(a) x-y 平面;(b) x-z 平面;(c) y-z 平面;(d) y-w 平面Fig.2.Phase portraits of chaotic attractor: (a) x-y plane;(b) x-z plane;(c) y-z plane;(d) y-w plane.
2.2 平衡点和稳定性分析
令(3)式的右侧等于0,计算其平衡点:
为了便于讨论,取a=6,b=41,c=1,d=0.5,e=10,h=1.1,求解出系统具有4 个平衡点,分别为
由于增加了系统的平衡点,也为产生多共存吸引子提供了可能.非零平衡点P1,P3对称的分布在z轴的两侧,平衡点P2,P4的情况相同.因为两组平衡点均关于z轴对称且都是方程的解,具有相同的性质,因此只需分别讨论平衡点P1和P2.
在平衡点P1处,系统对应的雅可比矩阵J为
求解其特征方程 det(λI -J)=0,得到相应的特征根为
因为λ1和λ2是一对含正实部的共轭复根,λ3和λ4都是负实数,因此平衡点P1是一个不稳定的鞍焦点.同理,可求得系统在平衡点P2处的4 个特征根分别为λ1=-104.808,λ2,3=-4.651±9.635i,λ4=0.372.其中,λ1是负实数,λ2和λ3是一对具有负实部的共轭复根,λ4为正实数,因此平衡点P2和P4均为三维空间的一个鞍点.综上,系统(3)的4 个平衡点均为不稳定平衡点.
系统(3)的耗散度∇V计算如下:
当取参数a=6,b=41,c=1,e=10,h=1.1,满足∇V <0,表明系统(3)是耗散的.
2.3 时域波形图和庞加莱截面图
取参数a=6,b=41,c=1,d=0.5,e=10,h=1.1,初始值为 (2,2,0.01,0.01),采用四阶龙格-库塔(ODE45)算法对系统(3)求解,可得系统状态变量x,y,z,w的时域波形如图3(a)所示,可以看出新系统为非周期系统.系统(3)在z=0 上的庞加莱映射如图3(b)所示,图3(b)存在无数个具有分形结构的密集点,表明系统具有复杂的动力学行为.

图3 系统的时域波形图和庞加莱截面 (a)时域波形图;(b)在 z=0 截面上的Poincaré截面Fig.3.Time domain waveforms and Poincaré cross section of the system: (a) Time domain waveforms;(b) Poincaré map on z=0 plane.
3 系统动力学分析
3.1 依赖系统参数变化的动力学行为
本节利用相轨迹图、Lyapunov 指数谱、分岔图、动力学地图等分析方法研究系统(3)的动力学行为.
首先选择a作为变化参数,设置b=41,c=1,d=0.5,e=10,h=1.1,初始值为Y1=(2,2,0.01,0.01) 和Y2=(-2,-2,0.01,-0.01),状态变量y随参数a在区间 (0,50) 变化的分岔图和Lyapunov 指数谱如图4 所示,其中蓝色轨线对应初始值Y1,红色轨线对应初始值Y2.当a ∈(0,2.4)时,4 个李氏指数均小于0,此时系统呈现点吸引子共存.在a=2.7 处,系统进入周期状态,随后经正向倍周期分岔进入窄共存混沌区域带.在该混沌区域中存在若干大小不一的周期窗口,系统表现出2 个周期1 吸引子共存,2 个周期2 吸引子共存的现象,如图5(a)和图5(b)所示.在a=11.86 附近,系统由混沌危机状态进入周期状态.而在a ∈(34.6,35)时,计算系统的4 个李氏指数分别为LE1=0.105,LE2=-0.322,LE3=-8.735,LE4=-38.460,其中有1 个指数大于0,系统表现出单涡卷混沌吸引子共存的现象,如图5(c)所示.当a >35 时,LE1在0 值上下波动,系统的吸引子在共存混沌和共存周期1 之间频繁切换.当a=50时,LE1=0,LE2,3,4<0,此时系统呈现另一种类型的周期1 吸引子共存,如图5(d)所示.

图4 随系统参数 a 变化的混沌动力学 (a)分岔图;(b) Lyapunov 指数谱Fig.4.Chaotic dynamics varying with system parameters a : (a) Bifurcation diagram;(b) Lyapunov exponential spectra.

图5 取 a 的不同值在x-y 平面的相位图(a)周期1 吸引子共存(a=3);(b)周期2 吸引子共存(a=3.2);(c)单涡卷混沌吸引子共存(a=34.93);(d)周期1 吸引子共存 (a=50)Fig.5.The phase diagram of different values in x-y plane: (a) Coexistence period 1 attractor coexistence (a=3);(b) coexistence period 2 attractor coexistence (a=3.2);(c) coexisting single scroll chaotic attractor (a=34.93);(d) coexistence period 1 attractor coexistence (a=50).
选取b ∈(10,80),初始条件为Y1=(2,2,0.01,0.01) 和Y2=(-2,-2,0.01,-0.01),绘制出系统状态变量y随参数b变化的分岔图和Lyapunov指数谱如图6 所示,其中蓝色轨线对应初始值Y1,红色轨线对应初始值Y2.由图6(a)可以看出: 随着参数b的不断增大,系统(3)呈现出了不同运动状态的吸引子共存行为.系统以共存周期行为开始,先后经历了倍周期分岔、切分岔和逆倍周期分岔等方式,在周期状态和混沌状态中切换,并最终稳定在周期状态.
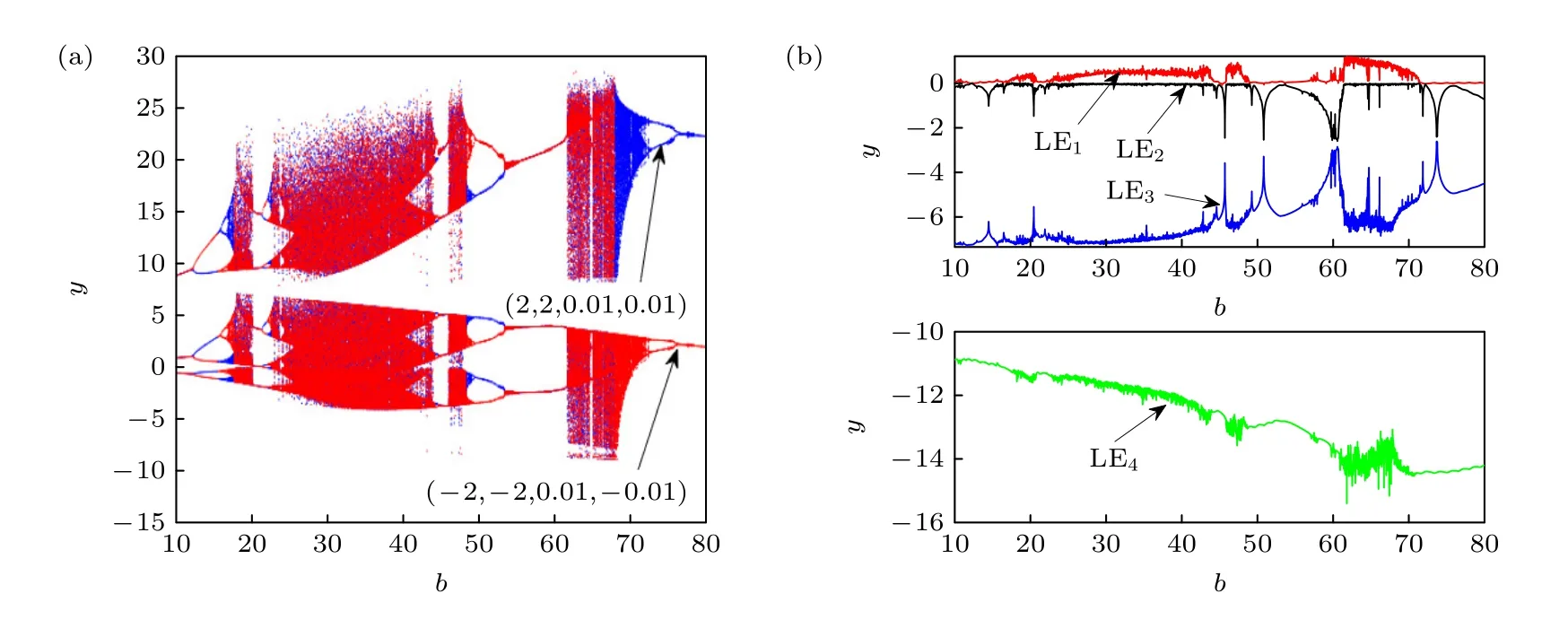
图6 随系统参数 b 变化的混沌动力学 (a)分岔图;(b) Lyapunov 指数谱Fig.6.Chaotic dynamics varying with system parameters b : (a) Bifurcation diagram;(b) Lyapunov exponential spectrum.
在这里选取了4 个典型的b值来模拟系统的动力学行为,其中包括周期1 吸引子共存、周期2 吸引子共存、双涡卷混沌吸引子共存以及单涡卷混沌吸引子共存的现象,分别如图7(a)—(d)所示.综合上述分析,可以看出: 相较于系统(2),由于忆阻非线性项和反馈项的引入,新构建的系统(3)确实表现出更复杂的动力学行为.

图7 取 b 的不同值在x-y 平面的相位图(a) 周期1 吸引子共存(b=10);(b) 周期2 吸引子共存(b=20.5);(c) 双涡卷混沌吸引子共存(b=62);(d) 单涡卷吸引子共存(b=70)Fig.7.Phase diagram of different values of parameter b on x-y plane: (a) Coexisting period 1 attractor coexistence (b=10);(b) coexisting period 2 attractor coexistence (b=20.5);(c) coexisting double scroll chaotic attractor coexistence (b=62);(d) coexisting single-scroll attractors coexistence (b=70).
图8 描绘了参数a和参数b变化时系统(3)的动力学特征,红色区域表示周期状态,蓝色区域表示混沌状态.从a=0 开始,纵向观察动力学地图的颜色变化,系统(3)一开始处于周期状态.当a=2.2时,从红色(周期)变为蓝色(混沌),在a ∈(2.3,35.3)区间中,有成片的蓝色区域包含细长红色(周期)小区域,说明系统(3)存在混沌与周期共存的状态.特别地,在红色区域内还存在几个线状和点状的蓝色区域,说明系统(3)在混沌和周期之间多次转换.
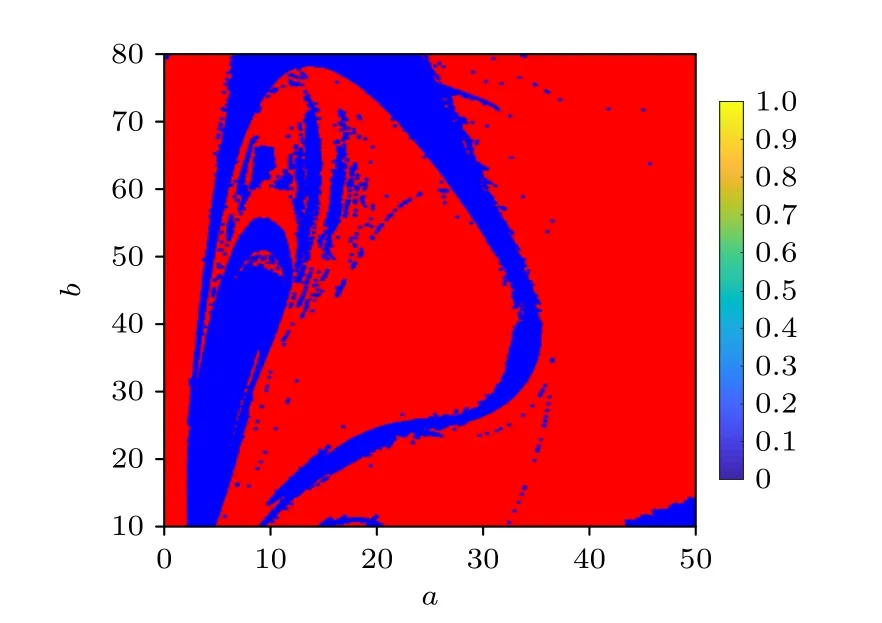
图8 参数a 和b 的动力学地图Fig.8.Dynamic map of parameters a and b.
3.2 依赖忆阻参数变化的动力学行为
分别选取初始值为Y1=(2,2,0.01,0.01) 和Y2=(-2,-2,0.01,-0.01),系统状态变量y随参数a1变化的分岔图和Lyapunov 指数谱如图9所示,其中蓝色轨线对应初始值Y1,红色轨线对应初始值Y2.由图9 可以看出,随着参数a1的增大,系统先经倍周期分岔由周期态进入混沌态,然后经逆倍周期分岔又由混沌态回到周期,在周期区间也夹杂着窄的混沌区间.而且系统还存在着周期吸引子共存、单涡卷混沌吸引子共存以及点吸引子共存等多稳态现象(详见表1 和图10).
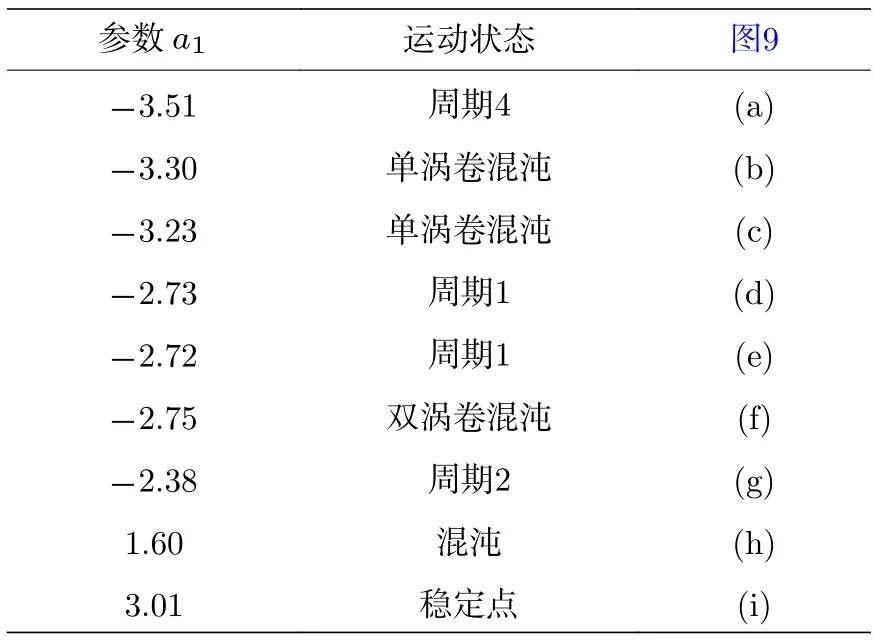
表1 不同 a1 值下的共存吸引子类型及图形编号Table 1.Types and figure numbers of coexisting attractors under different a1 values.

图9 随系统参数 a1变化的混沌动力学 (a) 分岔图;(b) Lyapunov 指数谱Fig.9.Chaotic dynamics varying with system parameters a1: (a) Bifurcation diagram;(b) Lyapunov exponential spectrum.
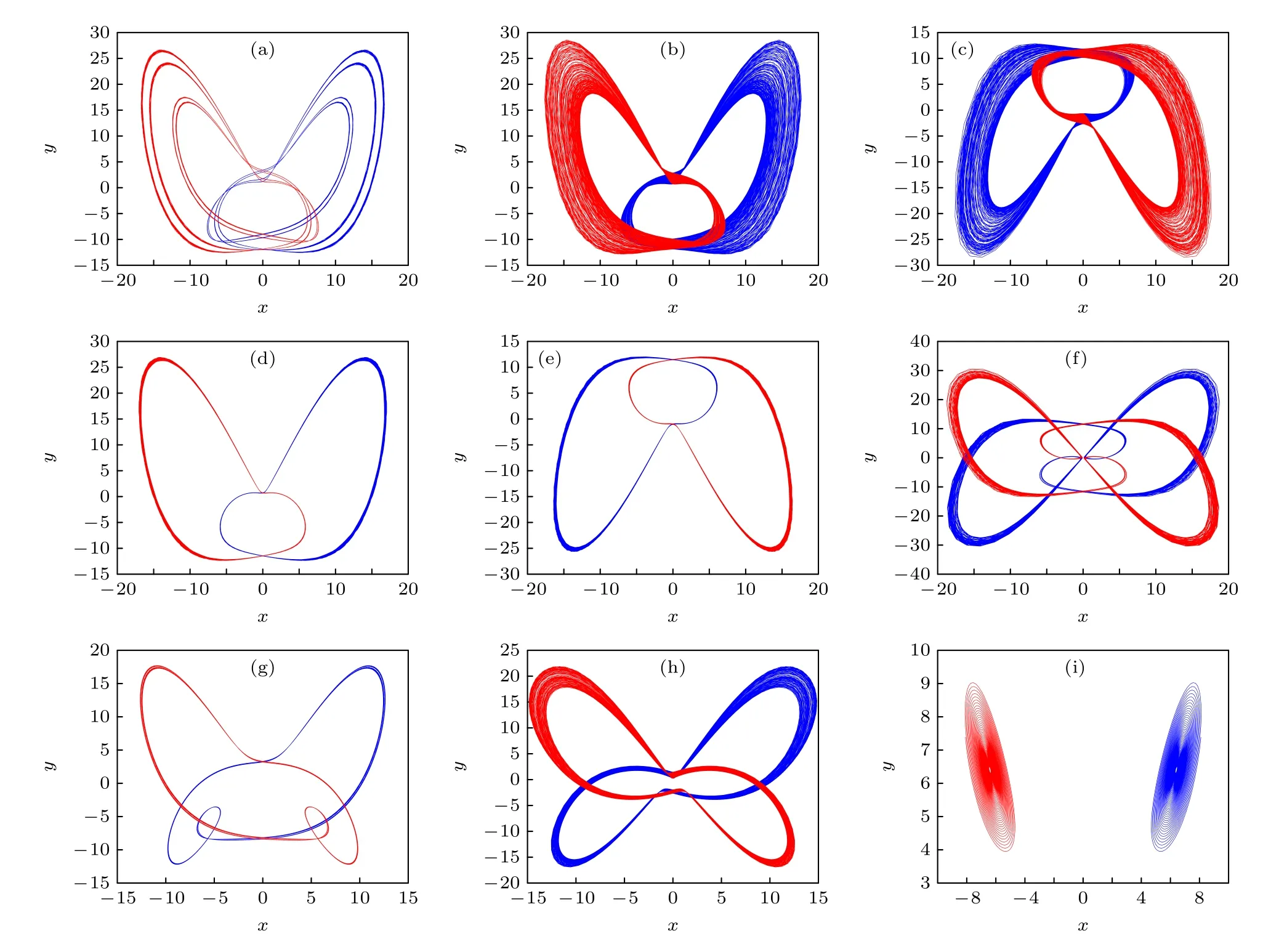
图10 不同 a1 值在x-y 平面的相位图Fig.10.Phase diagram of different values of parameter a1 on x-y plane.
特别地,从图10(b)—(e)可见,随着a1的增大,出现了两种情况的共存吸引子旋转现象,一对单涡卷混沌吸引子旋转,一对周期1 吸引子旋转.旋转是指对吸引子进行翻转或对折,从而改变吸引子原来的位置.在吸引子发生旋转的现象中,不仅出现由于系统参数改变引起的旋转,也存在由于系统初值改变引起的旋转.这一现象在以往的文献中并不常见,可见引入忆阻作为非线性项后丰富了系统的动力学行为.
4 系统的非线性反馈控制设计
4.1 理论分析
随着混沌控制的研究发展,学者们尝试采用不同的混沌控制方法如: 线性和非线性反馈控制法[29,30]、自适应控制法[31]和脉冲控制法[32]等去实现混沌系统的同步.本文采用非线性反馈控制法,研究具有不同初值,相同参数的两个新四阶混沌系统之间的同步问题,具体实现思路是: 首先将(3)式的混沌系统作为驱动系统,(3)式的复制系统作为响应系统,然后将非线性反馈控制器µ=[µ1,µ2,µ3,µ4]T施加在响应系统上,通过非线性反馈控制器消除驱动系统和响应系统的误差,以达到混沌同步的目的.
驱动系统方程:
响应系统方程:
为了获得实现驱动系统和响应系统同步的控制器,定义两个系统的状态误差变量为
将(9)式与(8)式作差,可得误差系统方程为
由上可得,可通过设置适当的控制向量µ使误差系统(11)在原点处稳定,从而实现驱动系统(8)式与响应系统(9)式的混沌同步.选择控制器为
其中,k表示反馈控制增益,将(12)式控制函数代入误差系统(11)可得
为了求解反馈增益k的取值范围,构建Lyapunov 函数如下:
式中,V(e) 为正定函数.结合(13)式,对(14)式沿误差e求导可得:
式中,a,c,e均为正值,故当k >0 时,必有(e)<0,即(e) 为负定函数.根据Lyapunov 稳定性定理,误差系统(11)以指数速率收敛到平衡点处,即对于任意给定初值,均存在,使驱动系统(8)式与响应系统(9)式达到同步.
4.2 数值模拟
本节通过在Matlab 上进行数值仿真,验证驱动系统(8)式与响应系统(9)式在非线性反馈控制器下是否达到同步.首先,选取系统参数为a=6,b=41,c=1,d=0.5,e=10,h=1.1,k=1,a1=1,b1=0.01,驱动系统(8)式的初始值为x1(0)=2,y1(0)=2,z1(0)=0.01,w1(0)=0.01,响应系统(9)式的初始值为x2(0)=3,y2(0)=3,z2(0)=1.01,w2(0)=1.01,步长设为0.02,仿真的同步误差收敛曲线如图11 所示,可以看出两个初值不同的系统在控制器作用下,误差e1,e2,e3,e4在1 s 前均已稳定在零点,即驱动系统(8)式与响应系统(9)式实现了混沌同步.

图11 混沌同步的误差收敛曲线 (a) e1 ;(b) e2 ;(c) e3 ;(d) e4Fig.11.Error convergence curve of chaotic synchronization: (a) e1 ;(b) e2 ;(c) e3 ;(d) e4.
5 FPGA 硬件实现
SOPC 是一种基于FPGA 的实现方案,系统的实现以AC620 FPGA 开发板为核心,如图12所示.选用的FPGA 为ED4 CE10 F17,SDRAM为W9812 g6 KH-6,大小为128 M,DAC 为双通道14 位AD9767.系统利用QuartusⅡ 17.1 软件定制开发,搭建SOPC 系统完成硬件设计.

图12 FPGA 实现设备Fig.12.FPGA implementation equipment.
选取系统参数:a=6,b=41,c=1,d=0.5,e=10,h=1.1,迭代步长 Δt=0.001,采用Euler法对系统(3)进行离散化处理,得到的差分方程如下:
利用C 语言编程,将量化后的数据经DAC 转换后输出到示波器,结果如图13 所示.可以看出硬件实现结果与数值仿真相图基本一致,验证了系统(3)的可实现性.
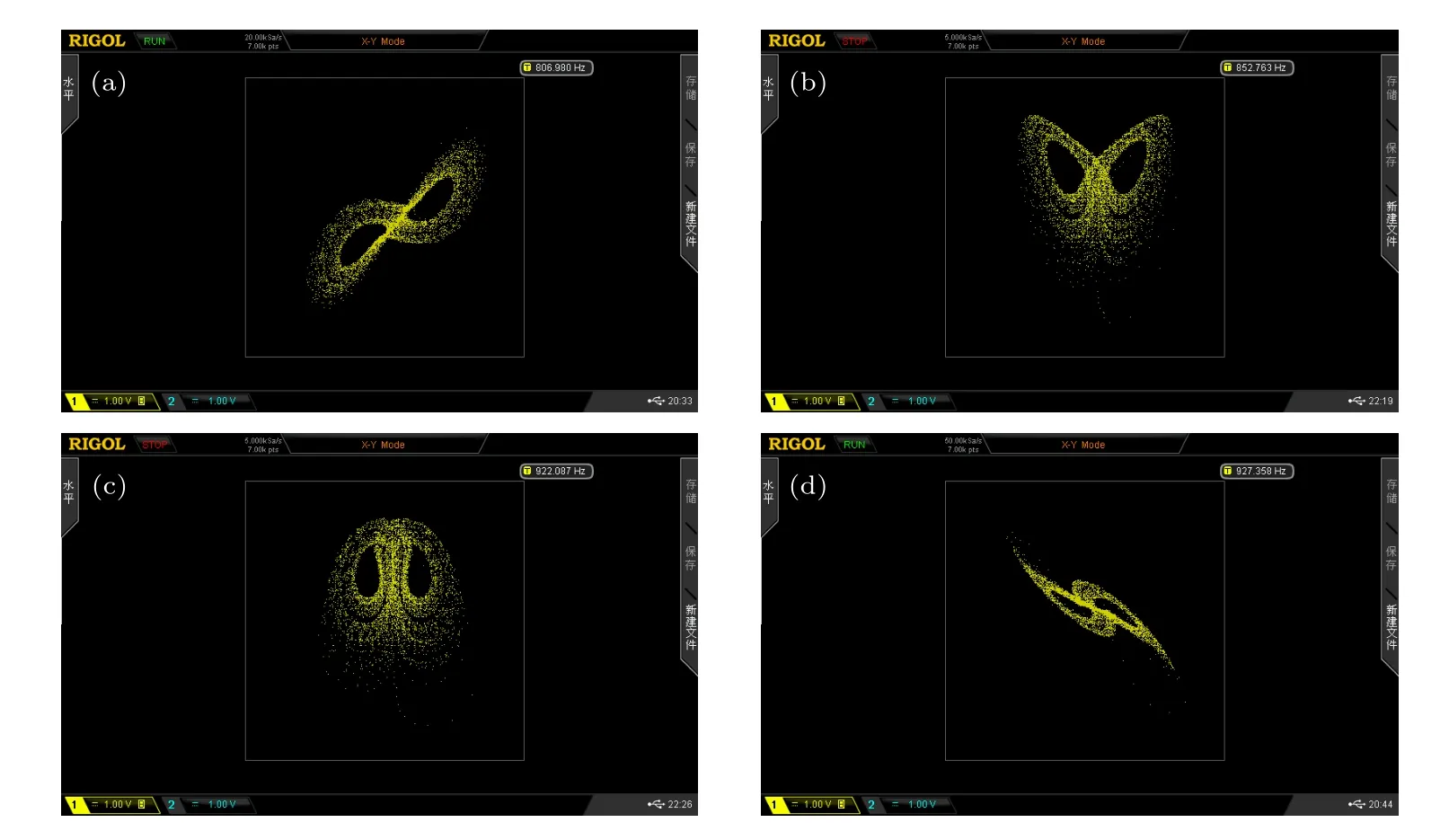
图13 FPGA 硬件实现系统相图(a) x-y 平面;(b) x-z 平面;(c) y-z 平面;(d) y-w 平面Fig.13.Realization of memristive chaotic attractor by FPGA hardware: (a) x-y plane;(b) x-z plane;(c) y-z plane;(d) y-w plane.
6 结论
将忆阻非线性项和状态反馈控制器引入三维自治二次类Lorenz 混沌系统,构建了一个新四阶混沌系统.通过数值分析发现该系统随着参数变化具有两个周期吸引子共存、两个单涡卷混沌吸引子共存、两个双涡卷混沌吸引子共存等多稳态现象,同时还发现了共存的旋转吸引子.其次,设计了一个非线性反馈控制器,实现了混沌系统的自同步.最后,通过FPGA 硬件平台实现该系统,实验结果与数值仿真结果保持一致,验证了系统的可行性,下一步将研究该系统在信息安全中的应用.

