基于机器学习的飞秒激光加工微坑阵列特征预测

王泽林， 王 冰， 宋海英， 刘世炳

(北京工业大学材料与制造学部 强场与超快光子学实验室， 北京 100124)

0 前 言

中国正处于从制造大国向制造强国转变的关键时期。 《中国制造2025》提出要加快新一代信息技术与传统制造业的深度融合，快速推动智能制造产业的发展。《新一代人工智能产业规划》将新一代人工智能提升到国家战略的高度，明确指出智能加工和制造是重点发力方向。 在该规划与《中国制造2025》的共同推动下，我国制造业智能化、自动化升级不断深化[1]。 现有的研究表明， 材料表面的微结构能赋予产品某些独特的功能或特性[2]。 微坑阵列是一种典型的表面微形式，主要制备方法有: 激光加工、电化学加工、电火花加工、超声加工等。 Byun 等[3]利用微细电解加工方法，在AISI 440C 不锈钢表面制备微坑阵列，成功降低了材料的摩擦系数，提高了材料的抗磨损性能。 Wang 等[4]通过喷砂、酸蚀与化学氧化的混合加工方法，在金属钛表面制备了微纳米复合的凹坑阵列结构，提高了材料的抗腐蚀性与生物相容性。 王文中等[5]采用激光加工工艺在圆柱形表面制备了微坑阵列结构，该结构表面的摩擦系数低于光滑表面，从而降低了摩擦力，提高了材料的润滑性能。 清华大学Lin 等[6]利用超快激光在玻璃表面制备了基于微坑阵列的微纳米复合结构，从而使材料具有超疏水、自清洁的特性，同时还保持了玻璃的高透光度。 相比于其他加工方法，激光加工属于非接触性加工，具有绿色环保、效率高、成本低廉等优点。在激光加工微坑的过程中，影响加工结果的因素有很多，加工状态随时在变化，且各种因素对微坑的几何形貌与加工质量影响复杂，呈非线性，因此建立准确的预测数学模型比较困难。 随着智能化技术的发展和应用，许多专家学者将机器学习算法应用到类似的加工结果预测上面。

顾峰[7]采用人工神经网络(ANN)算法建立了电火花方式加工小孔的预测模型，对加工工艺性能包括加工时间、电极损耗和孔径间隙进行了预测，并通过仿真模型验证了所建立的数学模型具有良好的预测效果和精度。 Campanelli 等[8]发现，使用ANN 模拟激光铣削过程，可实现模型预测值与实际值之间的误差低于5%的预测。 哈尔滨工业大学特种加工及机电控制研究所白基成等[9]采用MATLAB 中自带的神经网络工具箱构筑了基于径向基函数神经网络(RBF)人工神经网络的电火花小孔加工电极损耗预测模型。 该模型可实现深度可控的盲孔加工，模型的预测误差基本控制在9%以内。 Dinaharan 等[10]利用ANN 算法对铜表面复合材料的磨损进行了预测，预测值和实验值之间的差异小于5%。 Zhang 等[11]利用多种算法[深度神经网络算法、支持向量机、随机森林回归(RFR)等]对飞秒激光旋切小孔的特征进行了快速预测，之后利用遗传算法对加工工艺进行了优化，获得了最小锥度和最大加工效率。 Senthil Kannan 等[12]利用遗传算法对激光钻孔的锥度与材料移除速率进行了优化，显著提高了模型的预测能力。 Rajesh 等[13]利用自适应神经模糊推理系统对激光钻孔的锥度进行了预测，模型与实际实验数据拟合的R2达到0.903 5。 王冰等[14]利用迁移学习算法、k-means聚类算法、决策树算法、ANN 等多种算法对飞秒激光诱导纳米级表面周期性结构的结果进行了智能化分类，确定了最优加工窗口。

在实际应用中， 一个亟待解决的问题是使用不同的机器学习算法在不同数据集中所表现的效果存在着不一致性。 另一方面，基于决策树、RFR 等算法的模型具有可解释性，而基于神经网络的黑箱算法往往预测准确率更高。 因此，本研究在前人工作的基础上，利用RFR 算法与ANN 算法对飞秒激光加工微坑的结果进行了预测，对各个参量的影响进行了讨论，分析了不同方法的优劣。

1 实 验

1.1 实验装置

采用脉冲宽度为209 fs、中心波长为1 040 nm 的飞秒激光器(型号PHAROS)在亚克力(PMMA)材料表面制备微坑结构。 激光束由Scanlab 振镜系统控制，通过210 mm 焦距的f-theta 透镜(型号:SG2207－3D)聚焦。该光束具有TEM00(M2＜1.3)空间模式的高斯分布，聚焦光斑直径为35 μm。 完整实验装置如图1 所示。

图1 实验装置示意图Fig.1 Schematic of experiment set-up

1.2 数据采集

通过变换激光能量密度、脉冲次数和重复频率，实现不同直径、深度与表面粗糙度的微坑加工，研究激光加工参数对微坑形貌的影响，如表1 所示。

表1 激光加工参数选择Table 1 Selection of laser processing parameters

激光能量密度、脉冲次数和重复频率均分为6 个等级，共有216 种组合(6 × 6 × 6)。 激光能量密度选择加工凹坑阵列常用的能量密度范围，重复频率则从最高到最低选取6 个等级，脉冲次数选择1 ～10 的低脉冲次数，避免过高脉冲次数导致凹坑烧蚀严重、质量下降。 激光重复频率的调节，主要依靠调节PP(pulse picker，脉冲选择)来实现。 这种利用脉冲选择的调节方法，不会影响单脉冲的脉冲能量，同时降低了重频。通过快速扫描方法，使得到达材料表面的脉冲不互相重叠而实现单脉冲扫描，扫描速度为3 000 mm/s。 高脉冲次数可通过多次扫描实现。 采用共聚焦显微镜(OLYMPUS-LEXT-OLS4000)对凹坑的直径、深度、粗糙度进行测量，每组数据测量3 次，如图2 所示。

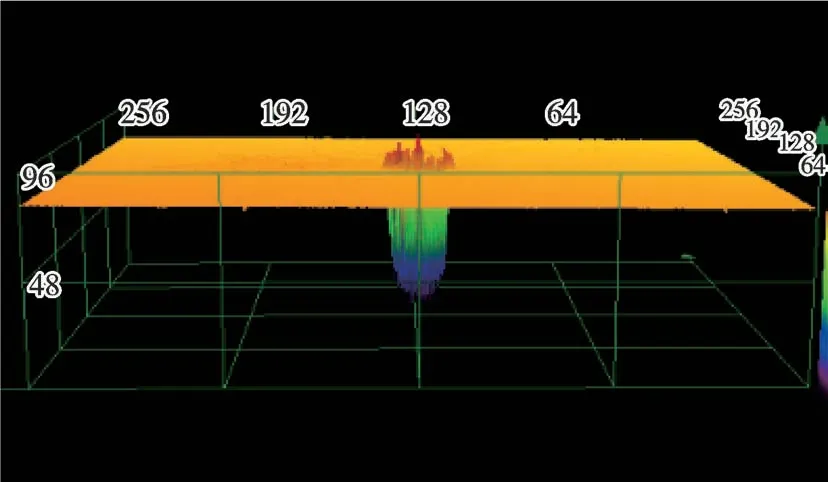
图2 共聚焦显微镜扫描的凹坑形貌Fig.2 Micro-pit topography measurement by confocal microscopy

1.3 RFR 算法模型

RFR 算法由Leo[15]提出，将分类决策树与Bagging算法相结合，形成一种集成学习算法。 分类决策树是二元分类器[16，17]，其通过2 个随机过程构建模型: (1)有放回地从训练样本数据集中随机抽取固定数目的样本作为训练样本集合； (2)每棵树使用的特征集是从总数据集中随机选取的少数特征。 通过组合多棵决策树，最终求平均值获得预测结果。 决策树的构建通常由非叶节点开始，选择特征的随机子集中的最佳分割点将数据进行二分类，且不断生长，当数据到达叶节点后不再划分。 为了将特征元素更合理地分布在非叶节点上，决策树通常采用基尼系数使信息增益最大化，见式(1):

式中:IG为基尼系数；s为待分类特征；Dp为父节点；Nl为左子节点样本数量；Np表示父节点中样本数量；Nr为右子节点样本数量；Dl为左子节点；Dr为右子节点。 对于特征s，在决策树生长过程中，利用式(1)计算出节点划分前后的不纯度之差，便得到不纯度衰减量。平均所有决策树得到的平均不纯度衰减量，最终得到该特征的重要性[13]。 对每个特征进行此操作，便得到所有特征的重要性，从而进行排序、筛选。

1.4 ANN 算法模型

ANN 是一种仿生网络结构，网络中的每个神经元都可以存储权值和偏置信息，并且不会受到其他神经元的干扰，因此网络中的神经元可以并行计算权值等信息，网络的信息计算速度比较迅速[18]。 由于网络连接的权值等信息是分布式存储，即使少量神经元的权值和偏置信息出错，整体计算结果所受的影响也非常小，所以ANN 的容错能力比较强。 ANN 还具有优异的非线性拟合能力，可以无限逼近任何非线性函数，具有拟合出加工中的加工参数和加工质量指标之间函数映射关系的能力。 如图3 所示，ANN 结构由输入层、隐藏层和输出层构成。 在本研究中，输入层为激光加工参数，包括激光加工功率、脉冲次数和重复频率。 隐藏层处理输入变量并调整神经元之间的连接属性，包括权重和偏置。 由于结果未知，需要连续调整隐藏层的权重和偏置，以获得最佳拟合结果。 输出层输出计算结果，其中包含3 个神经元节点，对应微坑的直径、深度和表面粗糙度。

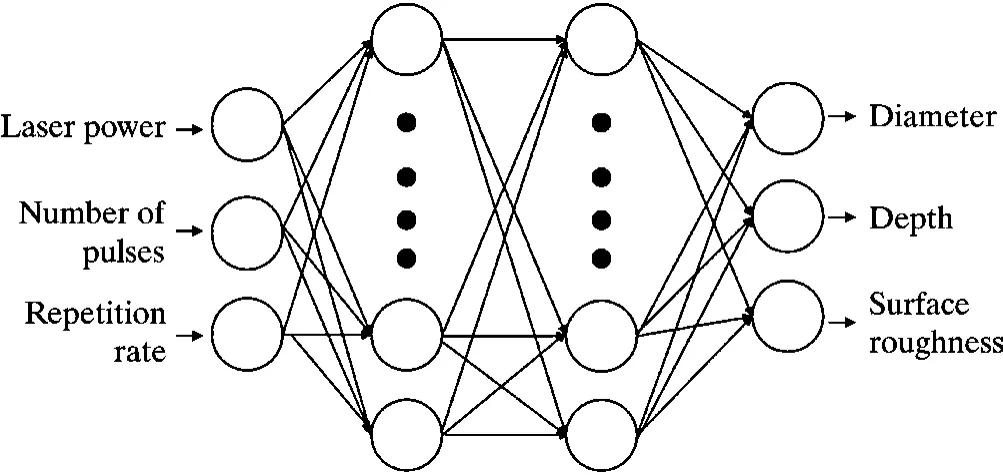
图3 人工神经网络示意图Fig.3 Schematic diagram of artificial neural network

1.5 模型评估指标

RFR 和ANN 模型的性能根据模型拟合程度和与目标值之间的偏差进行评估。 本研究采用3 个常用的评估指标对模型的预测能力进行评估，即确定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)，由下式给出:

2 结果与讨论

2.1 RFR 模型

2.1.1 RFR 模型预测结果

决策树的数量对模型的预测能力有重要影响，合理选择决策树的数量有助于减小模型的误差。 本工作首先利用k 折交叉验证法对决策树数量的影响进行了研究(见图4)。 如图可知，当决策树数量为35 时，预测误差最小，因此选择35 棵决策树的随机森林回归模型进行预测。 激光能量密度、脉冲次数和重复频率为模型输入参数，微坑的直径、深度和粗糙度为模型的输出。 选择176 个数据作为训练集，40 个数据作为测试集， 预测结果如图5 所示。 RFR 模型对于表面粗糙度的预测准确率最高，R2为0.80，对于直径的预测准确率最低，R2为0.70，深度的R2为0.73。 由图5 可知，在216个数据量下，RFR 模型对微坑结构整体的预测准确度并不是非常高。

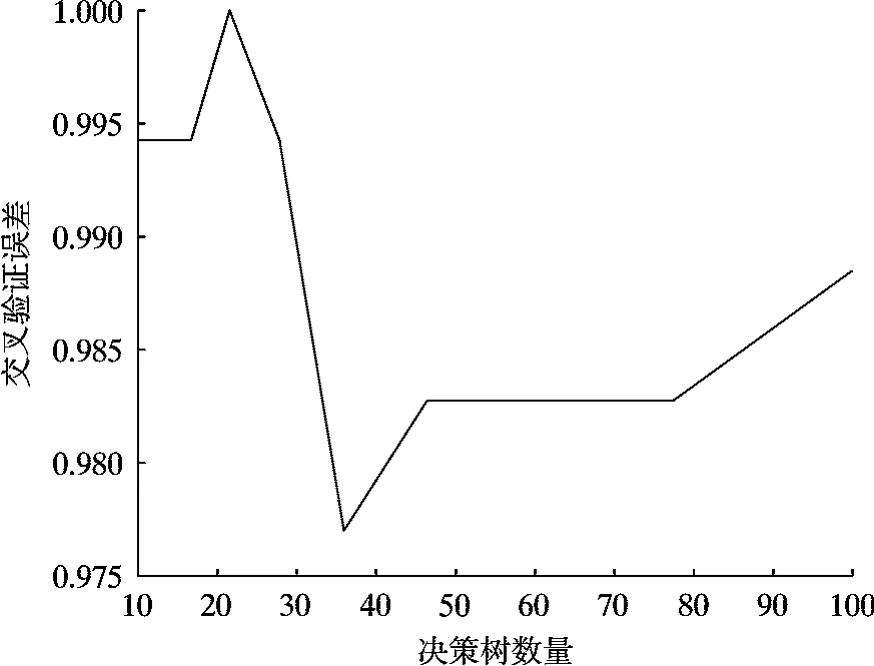
图4 决策树数量对随机森林回归模型误差影响Fig.4 Effect of decision tree quantity on the error of RFR model

图5 RFR 对微坑的预测回归图Fig.5 RFR prediction regression plot

2.1.2 加工参数影响分析

依据随机森林回归算法，计算了激光能量密度、脉冲次数以及重复频率对微坑的直径、深度以及表面粗糙度的影响指数，如图6～图8 所示。

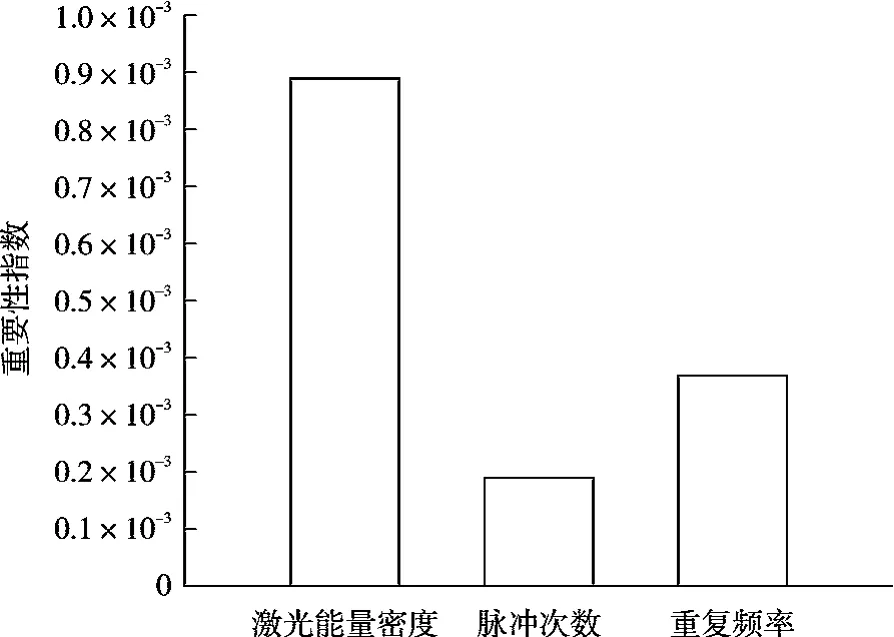
图6 激光加工参数对直径影响重要性排序Fig.6 Importance ranking of laser parameters on diameter

由图6 可知，微坑直径受激光能量密度影响最大，影响因子(重要性指数)达到了8.9×10－4，激光的重复频率对微坑直径的影响次之，影响因子为3.7×10－4，脉冲次数对加工直径的影响为1.9×10－4。 这与激光和材料之间的相互作用有关，当激光对材料进行加工时，能量超过烧蚀阈值的部分材料将会被移除。 由于光斑的高斯分布特性，当激光能量增强时，焦平面处超过材料烧蚀阈值的光斑直径增加，激光去除材料的能力增强，因而在微坑加工直径的形貌特征上，激光能量密度的变化对其影响最大[19]。

由图7 可知，飞秒激光的脉冲次数对加工的微坑深度影响最大，影响因子达到1.5×10－2，其次为激光的重复频率，影响因子为1.8×10－3，最后为激光能量密度，影响因子仅仅为0.4×10－3，对坑深度的影响非常小。 这是由于随着坑深的增加，坑壁面积不断增大，坑壁对激光能量存在吸收与散射，使得坑底部未加工的地方激光能量逐渐减弱，因而激光能量密度对微坑深度的影响较小。 伴随着脉冲次数的增多，不断地形成累积效应，使得微坑深度逐渐增加，因此脉冲次数对微坑深度的影响最大。

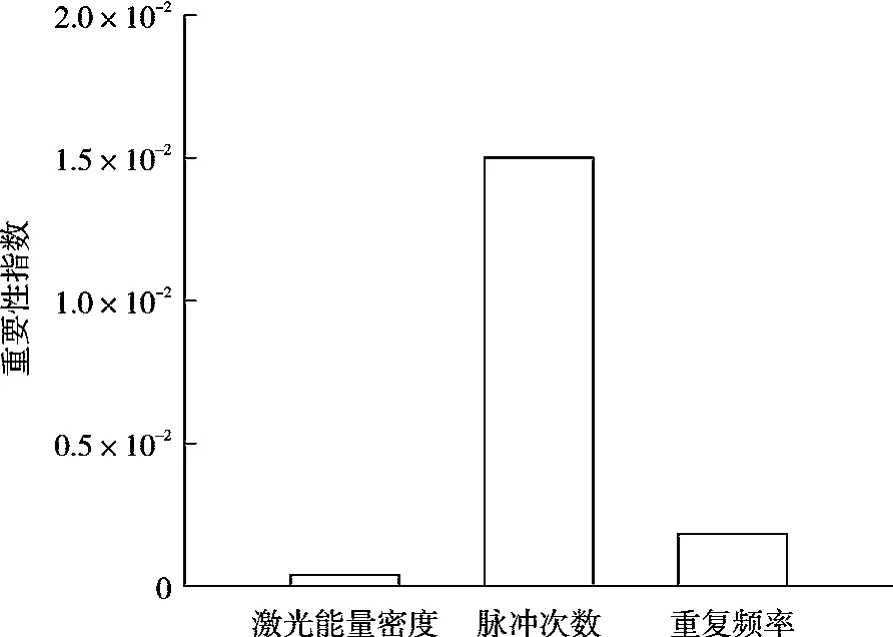
图7 激光加工参数对深度影响重要性排序Fig.7 Importance ranking of laser parameters on depth

由图8 可知，微坑的表面粗糙度受激光脉冲次数的影响最大，影响因子达到了4.5 ×10－2，这是因为多次的激光脉冲烧蚀，会使微坑表面形貌变差，粗糙度增加。 而激光能量密度和重复频率对微坑的表面粗糙度的影响因子分别为1.6×10－4和2.8×10－4，影响非常小[19]。

图8 激光加工参数对表面粗糙度影响重要性排序Fig.8 Importance ranking of laser parameters on surface roughness

2.2 ANN 模型预测结果

ANN 算法是一种黑箱算法，对于预测结果具有不可解释性，但ANN 模型可进行多目标回归，实现直径、深度与粗糙度的同时预测，模型预测结果如图9 与表2 所示。由图9 可知，ANN 在训练集上的R2为0.88，在测试集上的R2为0.64，验证集上的R2为0.53，整体R2为0.81。 验证集和测试集的拟合表现还存在较大问题，整体模型拟合度不高。 表2 所示为模型的整体拟合度R2与预测误差RMSE和MAE，图10 为ANN 模型在测试集上的残差图，可以看出预测值和实际值之间整体误差较大。

表2 ANN 整体模型对于直径、深度、粗糙度的预测准确率Table 2 Prediction accuracy of ANN model for diameter，depth and roughness

图9 ANN 对直径、深度与表面粗糙度的整体预测结果Fig.9 Prediction results of ANN model on width，depth and surface roughness

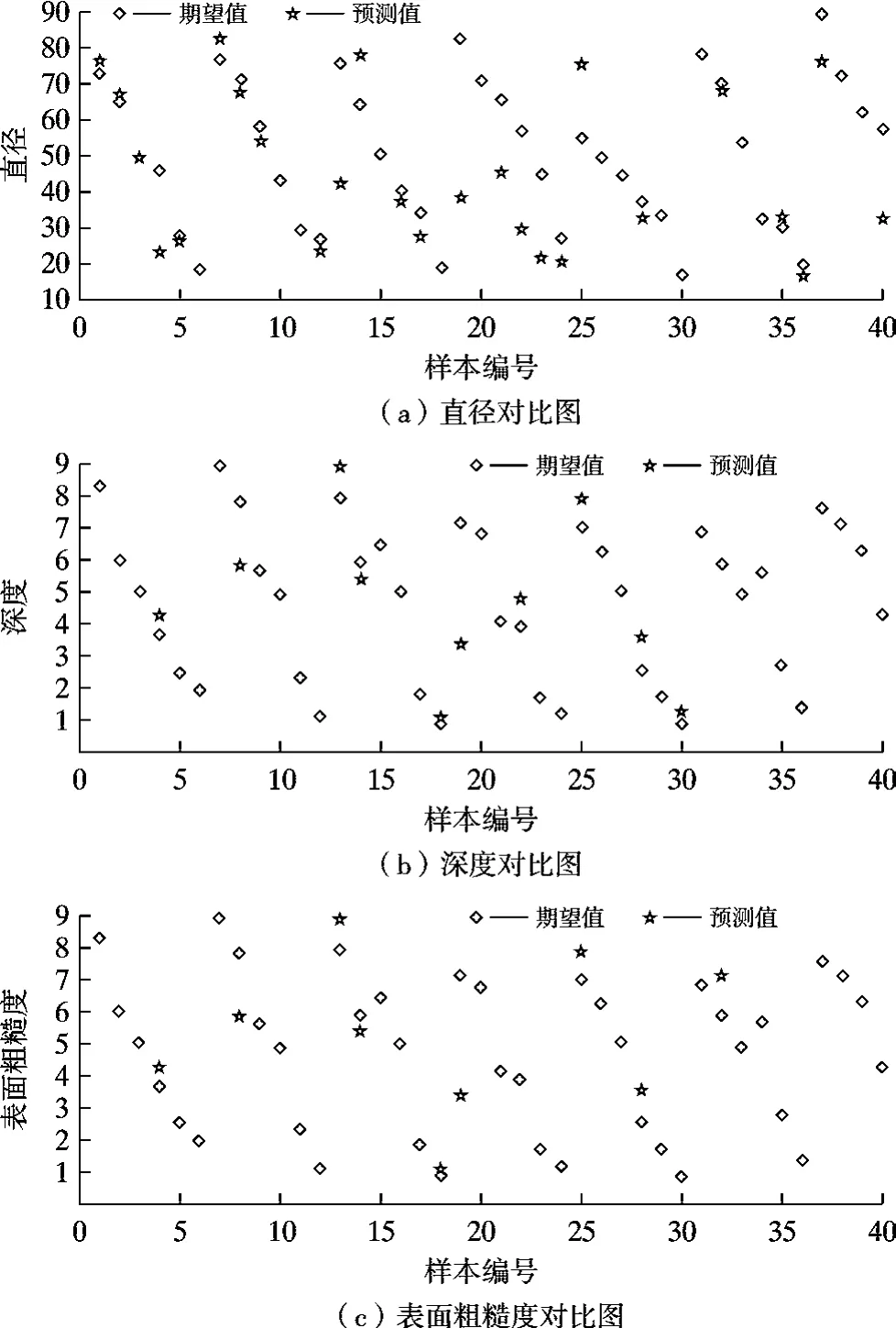
图10 ANN 模型算法预测值与实际值在测试集上对比图Fig.10 Comparison of target data and ANN model predicted data on test dataset

ANN 算法模型在对微坑的深度和表面粗糙度的拟合准确率较高，对直径的预测能力有一定的欠缺。 为了进一步提高模型的预测准确度，并与RFR 模型对比，将数据量扩充到648 个，然后对微坑的直径、深度和表面粗糙度再次进行预测， 预测结果如图11 所示， 训练集，测试集，验证集和整体的拟合度非常好，确定系数分别为0.90、0.86、0.86 和0.91，性能明显高于数据扩展之前的0.88、0.64、0.53 和0.81，扩展前后整体性能对比结果如表3 所示。 在大幅度增加数据量之后，ANN 模型算法对微坑的直径、深度和粗糙度的预测能力有了进一步提高，并且预测误差进一步下降，由此可见增加训练模型的数据量，可以显著提高ANN 模型算法对坑形貌的预测能力。

表3 ANN 算法数据增强前后模型预测性能对比Table 3 Comparison of model prediction performance before and after increasing data volume

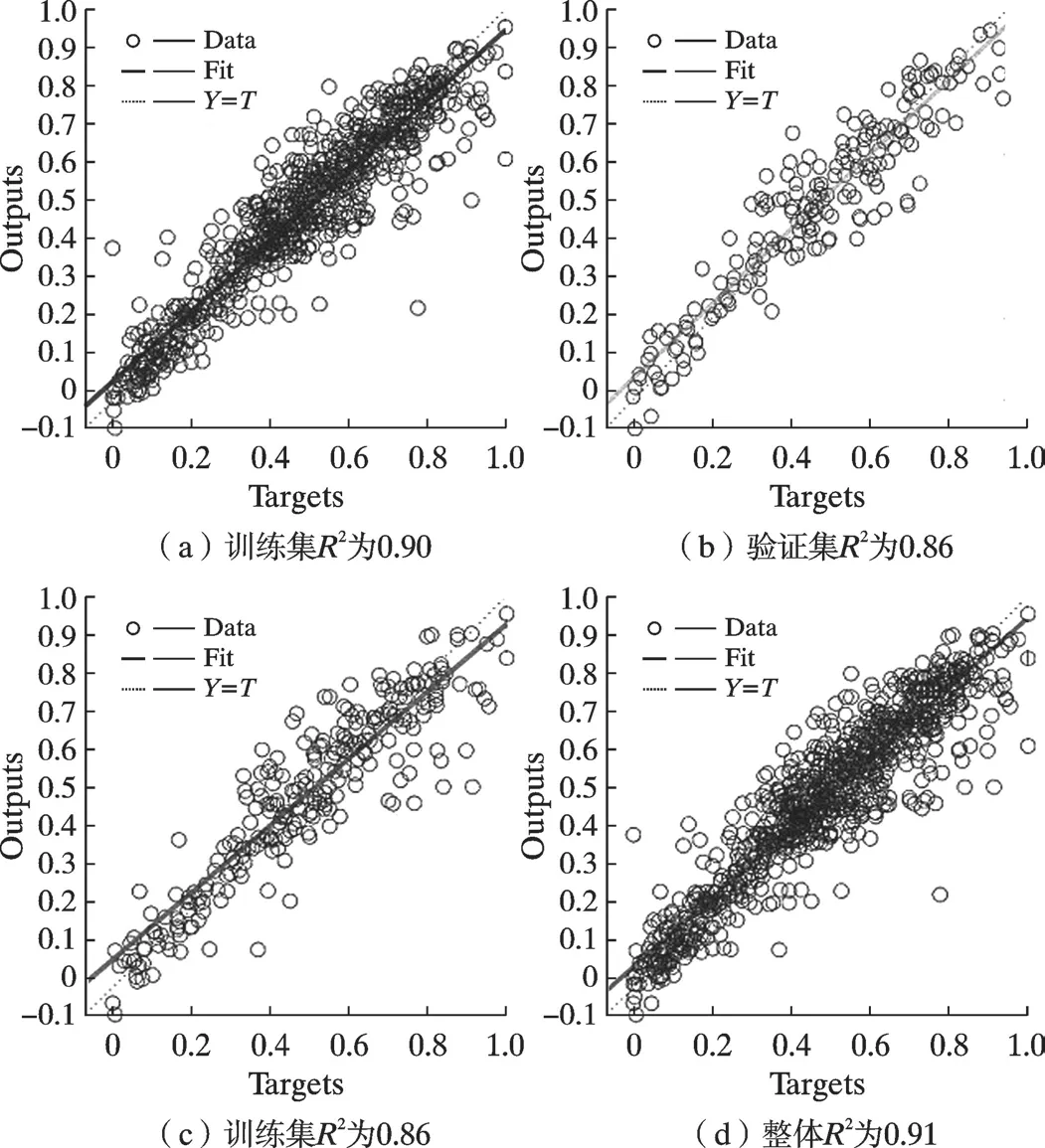
图11 ANN 对直径、深度与表面粗糙度的整体预测结果Fig.11 Prediction results of ANN model on diameter，depth and surface roughness

2.3 2 种算法对比

表4 展示了在648 组数据状态下，2 种算法的性能对比。 由表4 数据可知，RFR 和ANN 算法模型，在对微坑的深度和粗糙度的单独预测方面，都表现出了较好的预测性能，R2的值均高于0.80，相对拟合较好。 尤其在表面粗糙度的预测方面，2 种算法的确定系数(R2)值分别为0.92 和0.95，均方根误差(RMSE)分别为1.06 和0.62，平均绝对误差(MAE)为0.89 和0.46，误差值较小。 相比较而言，ANN 算法预测表面粗糙度方面性能优于RFR 模型算法单独预测的情况，拟合度更高，误差更小。

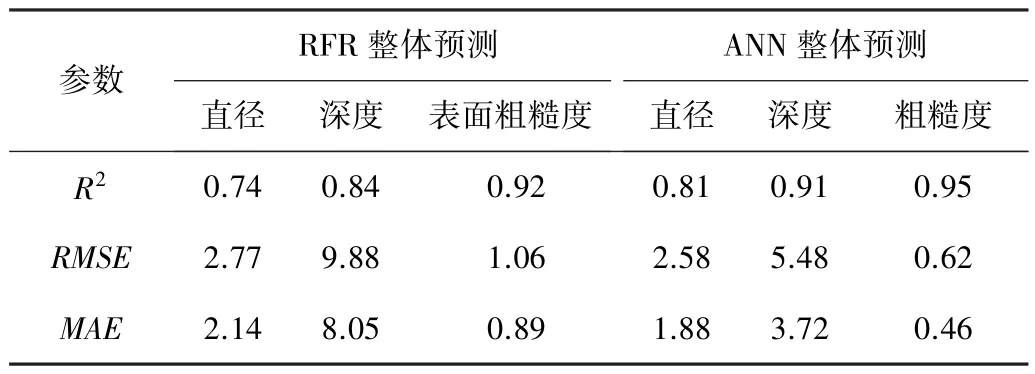
表4 648 组数据下RFR 算法和ANN 算法对比Table 4 648 data under RFR algorithm and ANN algorithm comparison

在微坑的直径预测方面，RFR 单独预测微坑直径的确定系数(R2)仅为0.74，低于ANN 模型算法整体预测情况下的确定系数(R2)0.81，同时ANN 模型算法整体预测情况均方根误差(RMSE)和平均绝对误差(MAE)单独预测情况下的值分别为2.58 和1.88，整体来说稍好于RFR 算法的2.77 和2.14。 在微坑的深度预测方面ANN 模型算法的确定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)分别为0.91、5.48 和3.72，准确率明显高于RFR 模型的3 项数值0.84、9.88和8.05。 这主要是由于ANN 算法有非常强大的非线性拟合能力。 ANN 算法由多个层和神经元组成，通过调控神经元之间的连接权重来拟合数据[20]。 RFR 算法是一种基于决策树的集成学习算法，由一定数量的决策树构建随机森林。 通过自助采样方法从原始训练数据中抽取样本来训练决策树，每个决策树抽取的样本有所不同，随机森林回归模型通过计算所有决策树的预测结果的平均值来进行最终预测[21]。 相比ANN算法，RFR 算法具有更好的泛化能力。 但ANN 算法非线性拟合能力更强，这种通过调节权重来拟合数据的方法相比RFR，在处理高度非线性和复杂数据结构的时候更具优势。 在本研究中，由于训练样本的限制，每颗决策树所训练的样本数量有限，也是造成RFR 算法准确率不高的原因之一。 此外，ANN 使用梯度下降等优化算法调节权重，而RFR 基于启发式搜索方法，参数优化上ANN 更加精确。

3 结 论

本研究开展了飞秒激光对PMMA 材料的微坑阵列加工研究，应用RFR 和ANN 2 种算法对微坑阵列的直径、深度和表面粗糙度(Ra)进行了预测，对2 种算法的预测性能进行了对比，具体结论如下:

(1)激光能量密度对微坑直径的影响最大，影响因子为8.9×10－4，脉冲次数对微坑深度与粗糙度的影响最大，影响因子分别为1.5×10－2和4.5×10－2；

(2)ANN 模型的整体预测准确率相比RFR 略高一些，R2值可达0.81，直径、深度、粗糙度预测R2分别为0.67、0.79、0.85。 RFR 模型对直径、深度、粗糙度的预测R2分别为0.70、0.73 和0.80；

(3)数据扩增后，ANN 模型与RFR 模型的预测准确率均得到提高。 ANN 模型在预测加工微坑直径、深度和粗糙度方面，确定系数(R2)分别为0.81、0.91、0.95，要好于RFR 模型的0.74、0.84 和0.92，整体误差性也要好于RFR 模型算法。