基于改进BBO算法和模糊期望效果的反导武器目标分配建模与实现

朱晓雯, 范成礼,*, 卢盈齐, 朱文正,2, 吴 暄

(1. 空军工程大学防空反导学院, 陕西 西安 710051; 2. 江南机电设计研究所, 贵州 贵阳 550009)

0 引 言

信息化作战条件下,反导作战环境日益复杂,武器目标分配(weapon target allocation, WTA)作为反导指挥决策核心问题,已成为国内外研究热点。由于敌干扰打击手段日益多样化,战场不确定因素不断增多,如何在不确定情况下合理利用现有资源、分配已有兵力和武器单元来打击敌来袭目标从而达到最优作战效果,是当前反导WTA亟待解决的问题。

在反导WTA问题的模型构建方面,传统WTA模型以最大化武器的预期损伤概率为目标,在此基础上还发展出基于成本的WTA[1]、基于资产的WTA[2]、基于传感器的WTA[3]、包含约束的WTA[4]、基于马尔可夫决策过程的WTA[5]及多目标多阶段WTA[6]等变体,但是基于效果的WTA研究仍然较少。文献[7]构建了基于物理毁伤效果最大化的效果WTA模型,但忽略了复杂战场环境下必然存在的不确定性特征。随着战场环境日益复杂,考虑到效果WTA模型中,包含主、客观多因素的目标意图价值和射击有利度具有明显的不确定特征,因而本文在分析和处理不确定因素的基础上,构建了基于模糊期望效果的反导WTA模型。

在反导WTA模型求解方面,由于WTA问题是典型的NP (nondeterministic polynomially)-hard问题,针对于NP-hard问题求解,启发式算法表现出良好的适应性,国内外学者提出使用差分算法[8]、遗传算法[9-10]、蜂群算法[11]、粒子群优化算法[12]等启发式算法对WTA问题进行求解。然而,进行大规模WTA的时候,现有算法都存在一定程度的算法复杂度高、模型求解速度慢、求解精度低的问题。因而,对于时效性要求较高的反导WTA求解仍然需要进行深入研究。基于生物地理学优化(biogeography-based optimization, BBO)[13]于2008被Simon首次提出,因具有能够通过迁入率和迁出率来增强信息交换和共享的特点,且求解效率和精度被原作者证明优于大多数启发式算法,对于求解NP-hard问题存在优势。

在BBO算法的优化方面,通常分为3类:基于迁移和突变操作的优化;与其他智能算法或精确算法混合;建立多种群或局部拓扑的BBO。在迁移和突变操作方面,张新明等[14]提出了稳定性较强,收敛速度快的BBO算法,结合了差分进化(differential evolution, DE)算法,并通过趋优变异对迁移和变异操作进行修改。罗锐涵等[15]对BBO算法增加了三维变异操作,对火力分配方案进行优化,增加了对于方案的全局搜索能力。Reihanian等[16]提出了新的BBO算法,并且在每一次迭代中使用两个及两个以上的子迭代过程,在每个子迭代过程中基于三角概率分布选择解进行迁移,同时使用了一种新的两相迁移算子,使算法实现勘探和开发能力之间的平衡。

与其他智能算法或精确算法杂交混合,Pushpa等[17]将烟花爆炸的概念融入BBO算法中,混合了两种不同的搜索技巧,以提高解的质量。Abu-Elrub等[18]将BBO算法的开发能力与粒子群优化算法的探索能力相结合,提出贪婪粒子群BBO算法。Zahran[19]等人利用BBO和入侵杂草算法构成新算法来求解射频识别网络规划问题,并提出自学习策略进行优化,该优化具有良好的性能。

在多种群或局部拓扑优化方面,Zheng等[20]将岛屿种群(解)视为一个具有局部拓扑结构的生态系统,模拟在生态地理屏障和分化下的物种扩散。Zheng等[21]将每个子种群分别进化为多个子种群,然后使子种群分别进化出一个改进的BBO,并对子种群的栖息地进行适应性评估,提出了一种基于合作的共同进化生物地理优化器。Kumar[22]等交替使用两种局部拓扑(即环形拓扑和方形拓扑)和一种全局拓扑结构来改善原BBO中全局拓扑而产生的计算密集、容易过早收敛的问题。

综合以上分析,可以看出BBO算法的改进集中于协调算法在集约化多样化搜索能力中的平衡,以及提升算法的效率和精度等方面。本文以反导作战WTA为背景,在考虑射击有利度和目标意图价值的不确定性基础上,建立基于模糊期望效果的反导WTA模型。为有效求解该模型,提出基于改进型BBO(improved BBO, IBBO)算法。该算法采用矩阵编码的方式,提出了栖息地动态选择迁移算子和DE的迁移算子,并采用余弦自适应因子将两种迁移算子融合;进一步,引入共生生物搜索算法中的相互作用思想对变异算子进行改进。仿真实例验证了该算法具有更高的求解精度和求解效率,能够有效求解大规模反导WTA问题。

1 模糊期望相关理论

1.1 模糊期望值理论

1.2 模糊期望模型

为了使期望决策最大化,可以建立模糊期望值模型[23]:

式中:x为决策向量;ξ为模糊向量;f(x,ξ)为目标函数;gj(x,ξ)表示约束函数。

1.3 模糊模拟技术

针对E[f(ξ)]的求解,可以采用模糊模拟技术[23],具体步骤如下。

步骤 1置e=0。

步骤 2分别从Θ中均匀产生θk,使得Pos{θk}≥ε,令vk=Pos{θk},k=1,2,…,N, 其中ε是个充分小的数。

步骤 3置任意实数a,b,a=f(ξ(θ1))∧f(ξ(θ2))∧…∧f(ξ(θN)),b=f(ξ(θ1))∨f(ξ(θ2))∨…∨f(ξ(θN))。

步骤 4从[a,b]中均匀产生r。

步骤 5如果r≥0,那么e←e+Cr{f(ξ)≥r}。

步骤 6如果r<0,那么e←e-Cr{f(ξ)≤r}。

步骤 7重复步骤4至步骤6共N次。

步骤 8E[f(ξ)]=a∨0+b∧0+e(b-a)/N。

步骤 9输出E[f(ξ)]。

2 基于模糊期望效果的反导WTA模型

2.1 传统WTA模型

传统的WTA模型通常以毁伤最大化为目标,建立在毁伤概率基础上。假设有n个反导武器平台,拦截m枚来袭弹道导弹。每个反导武器平台配有Ci枚拦截弹,各反导武器平台配备的拦截弹的总量不少于敌来袭的弹道导弹目标总量。可以建立模型[24]如下:

(1)

式中:maxE为最大毁伤效益;Pij为第i个武器平台被第j个目标毁伤的直接概率,0≤Pij≤1;Xij为第i个武器平台的对第j个来袭目标所使用的火力数量,形成关系矩阵[X]m×n。

该WTA模型主要考虑物理毁伤效益最大化,而未综合考虑目标意图价值和射击有利度等不确定因素,与实际作战不符。

2.2 不确定因素分析

现有的反导WTA模型大多属于确定型WTA模型。然而,由于实际战场环境的复杂性以及存在传感器误差、跟踪探测设备受干扰影响等不确定因素,决策模型中的参数往往具有不确定性特征,本文重点考虑以下两个方面。

(1) 目标意图价值。反导作战是不确定条件下的信息博弈过程,由于反导作战样式复杂多变,目标作战意图往往具有隐蔽性和欺骗性。来袭目标对我方攻击意图值越高,则应对其进行优先射击,以获得更大的毁伤和保护我方资产的效果。信息化条件下的目标意图不单需要掌握目标的速度、高度、航向角等状态信息,还需要挖掘洞见目标类型、机动行为和博弈策略等战术信息,因而具有很强的不确定性特征。

(2) 射击有利度。射击有利度受来袭目标的类型、来袭目标的飞行速度、航路捷径等多重因素影响,既包含主观因素,也包含客观因素,在复杂反导对抗环境下具有明显的不确定性特征。

本文将目标意图价值和射击有利度刻画为模糊变量,并通过三角模糊变量来表示。由于效果具有累积性,同时作战效果和消耗并不是完全对立的[25],为避免盲目消耗、摧毁,本文建立最大化费效比模型,用以衡量作战效果与消耗的关系。

2.3 考虑不确定因素的反导WTA建模

(2)

考虑到反导WTA模型所要解决的实际情况以及作战原则,模型中约束条件含义如下。

(1) 各武器平台可以同时打击多个敌来袭目标,且多种武器平台可以打击同一敌来袭目标,每个来袭目标至少分配一个火力。

(2) 每个武器平台配备多个火力,同一作战时间内每个武器平台对来袭目标分配的火力不能超过该武器平台的火力总数。

3 求解反导WTA问题的IBBO算法

与其他优化算法相比,BBO算法有一些明显的优势:不同的解方案之间共享属性,信息交流更为通常;原始种群在迭代后不会消失,而是通过迁移操作被修改;对候选解具有良好的挖掘能力和全局搜索能力;对于精英解的保留机制能使优秀的解方案在迭代中保存下来、不被修改。这些优势在求解反导WTA等NP-hard问题上存在一定的优越性。

但是BBO算法也存在易出现种群的多样性不高、迭代后期出现多个解相近、算法过早地收敛、变异方向随机等固有问题。本文主要从BBO算法的两个核心步骤——迁移操作和突变操作进行改进。在迁移操作中,设计栖息地动态选择策略的迁移算子和差分变异迁移算子,并融合两类迁移算子,提出余弦动态自适应选择策略,以提高算法在不同阶段的搜索能力。在突变操作中,提出基于共生策略的变异算子,以实现解分量的协同进化。改进后的IBBO算法具有种群多样性高、容易跳出局部最优、求解精度和效率都较高的优点,更加适用于求解反导WTA问题。

3.1 基本的BBO算法

BBO算法灵感来源于生物地理学中的物种迁移模型。自然界中的岛屿在BBO算法中被称为“栖息地”,适合物种居住的栖息地的生境适宜指数(habitat suitability index, HSI)相对较高,与这个指数有关的多种因素被称为适宜性指数变量(suitability index variable, SIV)。SIV可以看作为自变量,HSI可以看作为因变量,物种迁移的过程体现在迁移率中。图1为BBO算法的模型。

BBO算法的两个重要公式为

(1) 迁移操作

(3)

(4)

式中:μk表示第k个栖息地的迁出率;λk表示第k个栖息地的迁入率;E表示最大迁出率1;L是当前第k个栖息地的物种数量;N表示最大物种数量;I表示最大迁入率0;迁入率和迁出率都由栖息地的物种数量所决定。

(2) 变异操作

种群以一定的概率发生突变,这个概率为

(5)

式中:m(k)为第k个栖息地的变异率;mmax为最大变异概率;Pk为当前物种突变概率;Pmax为最大迁移修改率。

3.2 基于整数的矩阵编码策略

由于BBO算法主要采用整数编码,为便于操作求解,本文采取基于整数的矩阵编码策略对种群进行编码:

(6)

设Xij为一个物种,其中Xij代表第i个武器平台分配给第j个目标的火力数量。

由于栖息地生成时具有很强的随机性,且迁移和变异过程中可能会不满足约束条件或者超过边界。为了使约束条件成立,需要对每个栖息地进行可行性检查,即检查每个解是否符合约束条件的要求。本文提出两种修正算子,第一种修正算子运用在初始化种群后的可行性检查中;第二种修正算子运用在经过迁移、变异操作后的可行性检查中,具体做法流程图如图2所示。左侧为第一种修正算子运行流程,右侧为第二种修正算子运行流程。

图2 可行性检查流程图

3.3 基于余弦动态自适应策略的迁移算子

3.3.1 栖息地动态选择迁移算子

在BBO算法中的迁移机制,栖息地被选中进行迁移操作的概率和迁入率是成正比的,而其进行迁移的来源则与迁出率成正比。在选择中,原始算法主要采取轮盘赌的方式进行选择,这种方法可以让较优的栖息地大概率地被保留,并且使其SIV特征能够被选中并迁入较差的个体,从而使解不断更新并且进行优化。但这也很容易出现种群的多样性不高的现象,引起算法的局部收敛。

因而在不同的阶段中,进行迁入迁出操作时,需要进行不同选择压力的规定。在早期设置较小的选择压力,使HSI值较低的栖息地被选择修改的概率降低,从而一定程度上维护了种群的多样性,在后期设置较高的选择压力,使解集能够得到较快的收敛,从而更加趋近最优解。本文改进原始算法的迁移操作,提出栖息地动态选择迁移算子:

(7)

(8)

式中:Pk为第k个栖息地被选中的概率;popsize为种群数量;μk为第k个栖息地的迁出率;μi为任意第i个栖息地的迁出率;a为压力因子;Mmax和Mmin分别为压力因子的初值和压力因子的终值;G为当前迭代次数,Gmax为最大迭代次数。

本文选取较有代表性的多峰不可分Ackley测试函数在Mmax=1,Mmin=0的情况下运行得到结果如图3所示。其中,橙色线段为未改进的BBO算法。由图3可知,改进后动态栖息地选择前期收敛速度慢,有利于进行多样化搜索;后期收敛速度快,有利于加强集约化搜索,相同迭代次数内收敛精度较原始BBO有所提升。

图3 实验结果

3.3.2 差分变异迁移算子

DE算法[26]在1997年被Rainer Storn提出,其模拟了遗传学的基因变异等特点,在结构上类似于遗传算法,但是变异操作上略有不同。DE具有较强的探索能力,可以弥补BBO算法在迁移过程中的单一性,增强BBO算法的探索能力。本文将DE算法中的变异思想引入BBO算法的迁移过程中,提出差分变异迁移算子。

若有Gmax次迭代过程,则第G(G∈{1,2,…,Gmax})次的迭代过程中,通过随机选取3个不同的栖息地的SIV特征,分别为r1,r2,r3,并且满足r1≠r2≠r3,则可以得到有3个特征生成的新的变异变量:

Xij=Xr1j+F(Xr2j-Xr3j)

(9)

式中:Xij为第i个种群第j维解;Xr1j,Xr2j,Xr3j分别为选取的3个不同的种群的第j维的解;F为缩放因子,一般情况下取值为[0.5,1]。

3.3.3 余弦动态自适应选择策略

为使BBO算法在不同阶段能够适应性地提升搜索能力,在前期主要运用动态选择迁移算子进行修改,后期主要采用差分迁移算子修改。本文设计余弦动态自适应选择策略,该策略呈现动态震荡的余弦变化趋势,能够较好地融合动态选择迁移算子和差分变异迁移算子。余弦动态自适应因子如下:

(10)

余弦动态自适应因子随迭代次数增加的变化趋势如图4所示。在迭代前期随机概率小于α的概率较大,主要采用动态选择迁移算子进行修改,该算子有利于维持种群的多样性,避免局部最优的出现;在后期随机概率大于α的概率较大,主要运用差分变异迁移算子进行修改,这种算子更利于对解的探索,同时有利于算法收敛。余弦动态自适应因子随着迭代次数的变化动态变化并且总体收敛,有利于多种修改策略的协同作用,同时也有利于探索解方案的多样性,避免解重复或相近现象的出现。

图4 余弦动态自适应因子

该优化算子伪代码如算法1所示。其中,Population代表整个种群;popsize为解方案数量;Numvar1为矩阵编码的维度1;Numvar2为矩阵编码的维度2;lp为变量取值下界;up为变量取值上界;pmodify为最大迁移修改率。

算法 1 改进的迁移算子输入:Population, popsize, Numvar1, Numvar2, λ, μ, α, F, pmodify, lp, up输出:Population(1)For k=1 to popsize(2) If rand > pmodify(3) Continue(4) End if(5) For i=1 to Numvar1 (6) For j=1 to Numvar2(7) If rand < λ(8) If rand <=α(9) 根据变量取值界限(lp, up),运用式(7)和式(8)修改habitatk(SIVij)(10) Else (11) 根据变量取值界限(lp, up), 运用式(9)修改habitatk(SIVij)(12) End if(13) Else (14) habitatk(SIVij)=habitatk(SIVij)(15) End if(16) End for(17) End for(18)End for

3.4 基于共生策略的变异算子

原始BBO算法中的变异算子主要对于适应度值排序后的后1/2解根据变异概率进行变异。这种变异是随机进行的,有利于提升解的多样性,对于提供优秀解的可能较小。共生生物搜索算法[27]的互利共生思想是指对于生态系统中的某一个解方案随机选择生态系统中的另一个解方案作为共生对象,吸收相互之间的有利因素进行协同进化、互惠互利。

由于本文采用了矩阵编码的方式,矩阵第i行的每个解分量之间具有相互约束和协同进化的特点,可采用共生生物搜索算法中相互作用思想对变异操作进行优化,体现在公式中为

(11)

式中:Xbest代表了最优解;Xi和Xj分别表示选择的第i个解和第j个解;Xi(new)和Xj(new)表示产生的对应新解;BF1和BF2为收益因子,是随机整数值1或2;MV表示解i与j之间的关系向量。

进一步,考虑到矩阵编码中不同行列中的解分量数量不同,且相互约束作用,为体现协同进化,本文提出基于共生策略的的变异算子如下:

(12)

式中:n为矩阵第i行的解分量个数;BF为随机整数1或2;MVn为第k个解方案第i行的解分量之间的关系向量。

算法 2 改进的突变算子输入: Population, popsize, Numvar1, Numvar2, λ, μ, lp, up输出: Population(1) 用λk和μk计算Pk的概率(2) 根据HSI对Population进行排序(3) For k=poposize/2 to popsize For i=1 to Numvar1(4) For j=1 to Numvar2(5) If Pk>randMV=sum(Numvar1,:)/Numvar2 (6) 根据变量取值界限(lp, up),用式(12) 修改habitatk(SIVj) (7) End if(8) End for(9) End for

3.5 求解基于模糊效果反导WTA模型的混合智能算法

本文将IBBO算法与模糊模拟相结合,对基于模糊期望效果的反导WTA模型进行求解,求解步骤如下。

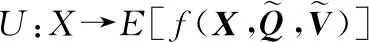
步骤 2设置相关算法参数,初始化种群,并检验栖息地可行性。

步骤 3计算每个栖息地的HSI值,并由优到劣进行排列,同时保留r个精英解。

步骤 4开始迭代。

步骤 5根据算法1进行迁移操作,对于每个修改后的栖息地检验是否满足约束,不满足约束的栖息地通过修正算子进行修正。

步骤 6根据算法2进行突变操作,对于每个栖息地检验是否满足约束,不满足约束的栖息地通过修正算子进行修正。

步骤 7重新计算栖息地HSI并检验栖息地可行性。

步骤 8对栖息地重新排列,并保存当前最优解。

步骤 9判断是否达到终止条件(最大迭代次数),如果是,则输出结果;如果不是,则返回步骤4。

求解模糊期望效果WTA问题的混合算法流程图如图5所示。

4 实验仿真分析

4.1 仿真实验假设

为验证基于模糊期望效果的反导WTA模型的合理性以及IBBO算法的有效性,给出以下实例:假设某次反导作战中我方武器平台数量为4,敌方目标数量为10,对应拦截弹均为25枚。射击有利度与目标意图价值的三角模糊变量如表1和表2所示。

表1 射击有利度

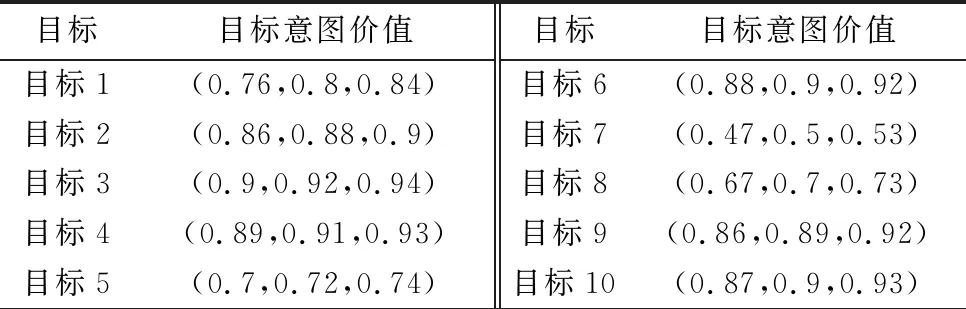
表2 基于效果的目标意图价值

4.2 测试及结果分析

4.2.1 算法参数测试

本文算法求解WTA问题时,除原始算法固有的参数外,产生的新参数有:压力因子a;压力因子初值Mmax;压力因子终值Mmin;比例参数θ。为测试不同算法参数对于最终结果的影响,本文选取参数范围内的离散值进行对比实验。

(1) 参数a,Mmax,Mmin

由于a通过Mmax和Mmin来确定,并且根据参数变化趋势需要符合算法由高到低的选择压力,因而在popsize=100;Numvar1=4;Numvar1=10;mmax=0.005;Pmax=1;F=0.5;θ=0.5;G=200的情况下,选取如下离散值进行20次独立实验,得到的结果如表3和图6所示。

表3 Mmax和Mmin取值比较

图6 不同Mmax和Mmin取值图像比较

由表3可以得到,随着Mmax的减小、Mmin的增加,算法得到的均值也呈现减小的趋势。由图6可以得到,Mmax和Mmin不同取值下HSI的变化趋势,其中Mmax取值较大而Mmin取值较小的时候,更加符合BBO优化时的选择压力由高到低的变化趋势。因而,选取较大的Mmax和较小的Mmin可以使WTA问题得到更优的结果。

(2) 参数θ

参数设置同上,Mmax=1,Mmin=0,结果如表4和图7所示。

表4 θ取值比较

图7 不同θ取值图像比较

由表4、图7分析可以得到,随着θ取值的增加,以及(1-θ)取值的减小,目标意图价值在效益值中所占比例提升,射击有利度所占比例减小,得到的均值也在不断增加,因而在实际战场情况中求解反导WTA问题时,需要根据具体情况确定θ取值。

4.2.2 实验结果

根据以上参数对于结果的影响分析,本文对参数进行如下设置:popsize=100,Numvar1=4,Numvar2=10,mmax=0.005,Pmax=1,F=0.5,θ=0.5,Gmax=200,Mmax=1,Mmin=0。

实验结果得到了最优的WTA方案,如表5所示。

表5 最优WTA方案

4.2.3 算法性能测试

本节在第4.2.2节参数条件下,分别在不同算法、不同种群规模以及不同战局规模的条件下进行对比实验以测试算法性能。目标函数随不同算法的迭代次数变化而变化的结果如图8所示。

图8 不同算法HSI变化曲线

将本文算法与文献[28]算法(简称为BBODE)、文献[29]算法(简称为BBOPSODE)、文献[30]算法(简称为NSBBO)、文献[14]算法(简称为DGBBO)、基本BBO这5种目前关于BBO优化改进效果较好的算法做了对比实验,得到的性能指标比较结果如表6所示。结合图8和表6可以发现,本文算法的求解精度最高,相较于原始BBO算法提升了5%左右,得到的最优解要明显高于其他几种算法。在运行时间方面,本文算法的运行时间仅次于基础的BBO算法,同时明显高于其他几种算法,较能满足分配方案的实时性要求。但最优解出现的代数较晚,分析可得:代数较少出现最优解的算法在迭代早期收敛,种群多样性不足,从而导致求解精度不高;本文算法在早期收敛速度较慢,通过改进的迁移和突变算子明显增强了种群的多样性,从而在后期使算法的精度有所提高。

表6 算法性能比较

表7为迭代次数和种群规模不同的情况下本文的最优值/平均值以及多次运行的平均运行时间,可以发现,最优值和平均值随迭代次数和种群规模的增加有一定程度的提升,因而为增加求解精度,可以适当地增加种群规模或者迭代次数。

表7 不同种群规模、迭代次数的最优值/平均值/平均运行时间

为了进一步验证算法在不同规模反导WTA问题下求解的有效性,对于不同规模的算例进行多次仿真求解。每种算例的规模分别为4×4(4个武器平台×4个来袭目标),10×10(10个武器平台×10个来袭目标)和50×50(50个武器平台×50个来袭目标),分别迭代200次,种群为100,分别运行后得到的仿真结果如表8和图9所示。

图9 不同算法在不同规模下箱线图

由表8可以发现,在不同规模的算例求解中,BBO算法相较于其他几种算法在求解运行时间上,求解中大规模的运行时间较优,明显高于BBODE、BBOPSO,NSBBO几种算法,在时效性上仍然较有优势。图9的箱线图中直观地显示了其最大值、最小值、中位值方面也明显优于其他几种相关算法。由此得出,本文算法能够适应求解大规模反导WTA问题并且提供求解精度更高、时效性更强的解决方案。

5 结束语

针对基于效果的反导WTA模型未考虑不确定性因素影响的问题,在模型构建方面,本文引入模糊期望理论,构建了基于模糊期望效果的最大化费效比反导WTA模型。在算法优化方面,提出了IBBO算法,设计了包含动态选择与差分变异迁移算子的余弦动态自适应策略,以及基于共生策略的变异算子,并结合模糊模拟技术形成混合智能算法,对模型进行求解。仿真实例结果验证了模型的合理性以及混合智能算法的有效性。该算法有利于大规模WTA问题的求解,并且能够适应反导作战对于时效性和求解精度的要求,能有效解决当前反导WTA问题中错分漏分的现象。下一步需要解决的是更加贴合战场环境的复杂动态多目标WTA问题。