具有大开距的塑壳断路器操纵机构优化设计

贾云博，许勇，杜静恩，刘凌霄，高美妍

（1.201620 上海市 上海工程技术大学 机械与汽车工程学院；2.201620 上海市 上海工程技术大学 航空运输学院）

0 引言

塑壳断路器（MCCB）是一种用来分配电能和保护线路以及电源设备免受过载、短路等故障危害的设备。随着低压电气行业的技术进步以及国家“双碳”战略，光伏、风能发电得到迅猛发展，电网内对于断路器的电压以及性能需求越来越高[1-2]。与交流电相比，直流电由于没有自然过零点，需利用电弧电压高于电源电压，迫使其过零点从而熄灭电弧[3]。直流系统具有更大的阻抗，分断时电流幅值更高，系统中存储了大量的电感，需要吸收的能量更大[4]，因此分断更加困难。

断路器中操纵机构动触头在分闸状态时与静触头之间的最短距离称为开距。研究表明，开距增大可以拉长电弧、降低电弧电压，从而有效提高断路器分断高电压的能力[5]。塑壳断路器操纵机构由于结构复杂，各设计参数相互耦合制约，不易优化。简便方法是增加动触头杆长度，此时为满足触头压力以及维持设计温升值，触头扭簧和主簧参数也需要调整[6]，这种方法虽然可以在不改变机构的情况下增大开距，但也有很大局限性，动触头长度不可以无限制增长。动触头增长会由于自重增加影响分断速度，且会给整个壳架尺寸带来一定影响。

本文对机构运动原理进行研究，建立操纵机构数学模型，对影响塑壳断路器开距的因素进行优化分析，并对结果进行了仿真验证，对于大开距直流塑壳断路器以及高性能塑壳断路器的优化具有一定的理论价值和工程实际意义。

1 结构组成及工作原理分析

塑壳断路器主要由操纵机构实现分、合闸动作，操纵机构是一个可在四连杆和五连杆间切换的可重构连杆机构。图1 所示为某型号塑壳断路器机构模型示意图，塑壳断路器有4 种动作模式：合闸、分闸、自由脱扣和重合闸[7]，其中，重合闸是发生自由脱扣后通过扳动手柄恢复至分闸状态的过程，由五连杆转变为四连杆状态。

图1 塑壳断路器机构模型示意图Fig.1 Schematic diagram of molded case circuit breaker mechanism model

塑壳断路器机构如图2 所示，A—G为转动副，1—5 为5 个连杆，是机构运动的主要组成部分，6表示跳扣限位件，10、11 为手柄限位件，12 为上连杆限位件，主弹簧两端连接着操作手柄7 和转动副C，8 为锁扣，9 为跳扣，14 动触头附着在13动触头杆上，主轴杆4 和动触头杆13 通过扭簧力压在一起，15 为静触头，与机架固接。

图2 塑壳断路器操纵机构简图Fig.2 Schematic diagram of operating mechanism of molded case circuit breake

合闸状态时电网为通路，机构简图如图2（a）所示，合闸动作前为分闸状态，机构简图如图2（b）所示。跳扣由于受到主簧拉力的影响，有绕转动副A逆时针转动的趋势，锁扣8 将跳扣AB限制住，此时机架为BE，杆DC、CB、BE、ED组成四连杆。合闸时，手柄7 受到力矩逆时针转动，主弹簧14进行储能，当主弹簧力方向与BC杆重合，再继续推动手柄时，主簧释放能量，拉动BC杆绕B点顺时针运动，由于四连杆机构具有一个自由度，BC杆作为原动件，机构进行合闸动作；分闸过程和合闸过程相反，由图2（a）运动到图2（b）的过程仍为四连杆机构。手柄受到外界施加的力矩发生顺时针转动，主簧力轴线过BC杆时，使BC杆逆时针运动，动触头迅速抬起，到限位杆6 位置停止。

自由脱扣状态机构如图2（c）所示，当电网中发生短路、过载、欠压等故障时，能够迅速断开电路保护设备安全，发生电路故障后，通过外部机构使锁扣8 绕G轴顺时针转动，跳扣9 解锁并在弹簧力作用下绕点A逆时针转动至限位杆6，BC杆也受到弹簧力的作用逆时针动作，动触头14快速抬起拉断电弧，此时AE为机架，和杆DE、CD、BC、AB组成五连杆，具有2 个自由度。

图1 中开距在图3 中表示为d，静触头移开后，动触头还能够超行程移动的距离称为超程s。超程的存在是为了保证触头压力，从而减小触头电阻。连杆DE 的运动角度θ（又称为主轴旋转角）和开距d、超程s以及触头杆长度L的关系为

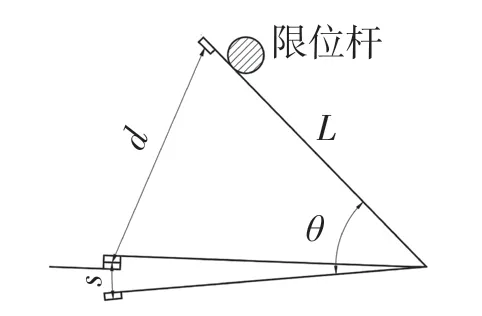
图3 主轴旋转角θ与超程s、开距d 示意图Fig.3 Schematic diagram of spindle rotation angle θ,overtravel s and opening distance d

为了保证考虑磨损在内的合闸可靠性以及合理的触头压力，不同型号的断路器有不同的超程标准范围，而增加触头杆长度受到多种因素限制，且不利因素较多，因此把针对大开距的优化转化为针对主轴旋转角的优化。

2 操纵机构运动学模型

塑壳断路器的分合闸为人工的常态化操作，真正对电网起到重要保护作用的是自由脱扣状态，因此对自由脱扣阶段的五连杆机构进行研究。操纵机构五连杆机构运动学模型及坐标系建立如图4 所示，以跳扣旋转轴和主轴旋转轴为机架，即AE为机架，以A为原点，AE方向为X轴，垂直于AE方向为Y轴，建立直角坐标系，5 个杆长度分别为l1、l2、l3、l4、l5，每个杆对应与坐标轴X方向的夹角分别为θ1、θ2、θ3、θ4，θ5为AE 与X轴夹角，固定为0°。图4（a）为刚脱扣时的五连杆运动学模型，图4（b）为自由脱扣结束后的运动学模型。

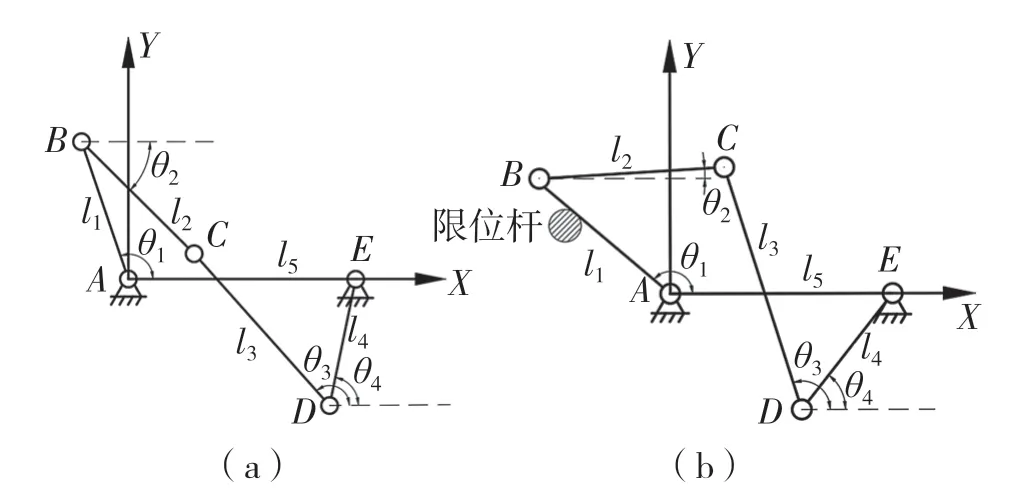
图4 以杆长为自变量的操纵机构运动学模型Fig.4 Kinematic model of control mechanism with rod length as independent variable

根据矢量投影法

将矢量投影到坐标轴上可得

令a=l1cosθ1+l2cosθ2-l5，b=l1sinθ1+l2sinθ2，式（4）可化为

式（4）对时间t求导，得速度方程

用坐标旋转法，式（8）中角度逆时针旋转θ3，即每个角度减去θ3，得角速度公式

3 塑壳断路器操纵机构优化模型

3.1 设计变量

塑壳断路器由闭合到分断的过程尤为重要，是衡量断路器性能优劣的重要指标，机构的各个杆件长度以及角度对于主轴的旋转角度有着十分重要的影响。分断过程为四、五连杆转换的过程，五连杆有2 个自由度，由上文运动学分析可知，若要确定机构运动状态，需要确定式（10）的7 个参数

其中，l1～5为优化目标参数，θ1、θ2的边界值由限位件确定，任意改动会影响机构整体强度，且小范围内改变角度设计值对于结果影响不大，因此作为函数输入值。

3.2 目标函数

目标函数是衡量塑壳断路器性能指标的函数，大开距设计时，由于触头行程增大，必然造成打开速度的损失。本文目的是在满足大开距的情况下，对机构参数进行优化以降低分断速度的损失，选择连杆机构的瞬时速度的加权组合平均数作为操纵机构的目标函数，指标函数越大机构的运动性能越好。

式中：Wk(X)——连杆瞬时速度；X——设计变量。

3.3 约束条件

（1）边界约束：xmin≤xi≤xmax，i=1,2,3,4,5。xmax和xmin为设计变量的上下界，由壳架尺寸相关参数决定，即：

（2）角度约束：根据合闸时的连杆位置状态，为避免出现奇异位型，增强结构的可靠性，有π ≤θ2+θ3≤π，即：

（3）运动行程约束：运动行程影响开距的大小，约束值受不同断路器结构和限位件影响，本文约束为某种结构的设计值，为方便描述，断路器闭合和断开状态各参数下标分别设为c、o。根据式（6），在闭合和断开状态的大开距运动行程约束为

且分别设θ1c=143°，θ2c=5°，θ1o=109°，θ2o=-45°。

3.4 优化模型求解算法

本文使用粒子群算法对塑壳断路器操纵机构优化模型进行求解。粒子群算法（PSO 算法）是一种基于群智能行为的全局优化算法，由Eberhart 和Kennedy 博士发明[8]，由于算法容易实现、没有太多参数需调节且结果收敛性较好，已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他算法的应用领域[9-10]。每一次迭代都会对粒子群体最优解Gbest和个体最优解Pbest比较后更新粒子的速度和位置，粒子速度和位置更新的公式为

式中：xi——设计变量；，——个体xi的第t次和第t+1 次迭代速度；ω——惯性权重系数；c1，c2——学习因子，根据经验设置取值区间为[0,2]；r1，r2——0～1 的随机数；Pbesti——个体xi的最佳位置；Gbesti——种群中的全局最优位置；——设计变量在第t+1 次迭代后的位置。

惯性权重ω是粒子迭代过程中的重要参数，其大小影响算法的全局和局部搜索能力，为了平衡搜索能力，ω设为自适应参数。当粒子适应度值较大时，表明粒子的搜索方向是正确的，此时将ω的值设置为较小值，使粒子更加注重自身的局部搜索能力；当粒子适应度值较小时，表示粒子在当前方向搜索结果与最优解相差较大，此时将ω设置为较大值，以提高粒子的全局搜索能力。因此，惯性权重ω的自适应更新方法为

式中：ωmax，ωmin——设定的惯性权重的最大值和最小值，一般分别取0.9 和0.4；F——适应度函数；Favg——第t次迭代时适应度函数的均值；Fmin——第t次迭代时所有粒子适应度函数的最小值。

3.5 优化结果

使用Python 3.10 版本进行算法调试和求解，初始条件设置如下：种群大小为200，迭代次数设为500，学习因子c1=c2=1.49，连杆参数优化前后如表1 所示。根据表1 以及位置方程可以得到优化前的主轴旋转角为39.973°，优化后的主轴旋转角度为49.653°。

表1 杆长参数Tab.1 Rod length parameters

目标函数迭代寻优曲线如图5 所示，在50 代之内算法有效收敛，说明算法的优化速度很迅速，而优化结果是否正确需要对机构进行仿真验证。

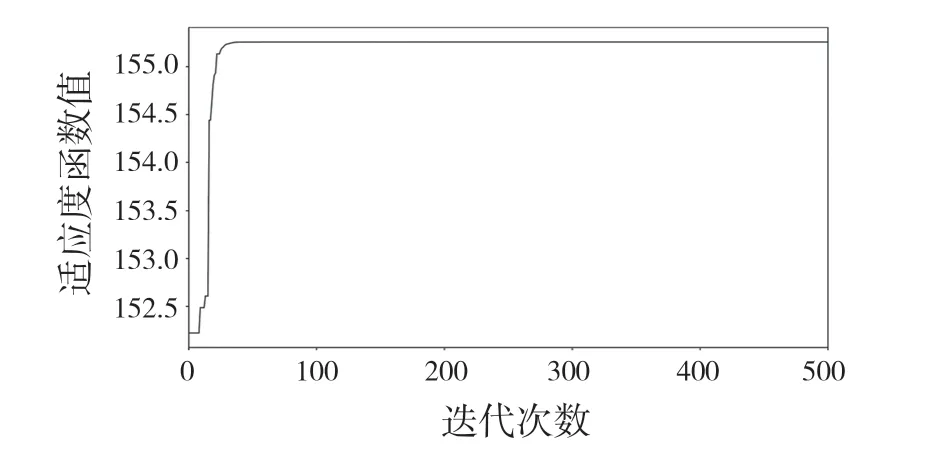
图5 目标函数寻优迭代曲线Fig.5 Objective function optimization iteration curve

4 仿真分析

在SolidWorks 中对操纵机构进行建模，然后导入动力学仿真软件ADAMS，对部分机构进行参数化建模，图6 为塑壳断路器操纵机构三维模型，根据实际运动情况添加必要的约束和驱动[11]。

图6 ADAMS 塑壳断路器操纵机构仿真模型Fig.6 Simulation model of MCCB operating mechanism based on ADAMS

运行仿真并测量，仿真塑壳断路器在分断时的过程，并在后处理中输出动触头旋转角度仿真曲线。图7 所示为优化前参数动触头的旋转角度与时间关系曲线，可以得出从仿真开始到5.8 ms 完成分断过程，此时动触头旋转了40.2°，由于模型精度以及仿真误差，与计算结果39.973°略有偏差。

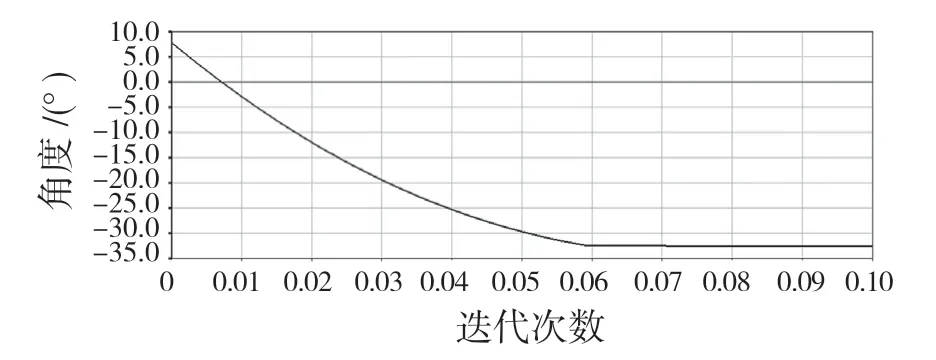
图7 优化前动触头旋转角度Fig.7 Rotating angle of moving contact before optimization

调整各坐标点的位置，使各杆长度达到优化后的参数值，再次运行仿真，并在后处理中输出动触头旋转角度仿真曲线，结果如图8 所示。

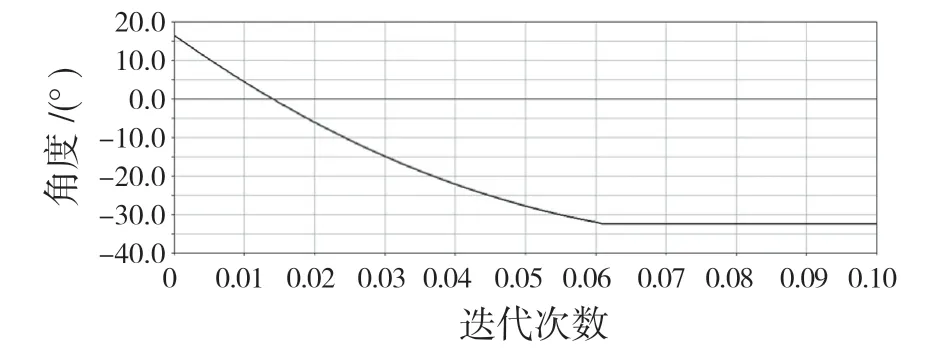
图8 优化后动触头旋转角度Fig.8 Rotation angle of rear moving contact after optimization

由图8 可见，6.2 ms 之后完成分断过程，动触头旋转角度为49.2°，计算结果为49.653°，与优化前相比旋转角度更大，可获得更大的开距，分断时间仅降低0.4 ms，对此可适当提高主簧的簧力，使机构有更快的分断时间。除此之外，对于一些限位件和操作手柄旋转角度也应有适当的调整。

5 结语

（1）本文对塑壳断路器的动作模式进行分析，建立其位置模型，并求解得到动触头转角以及运动速度方程，为进一步进行结构优化奠定了基础。

（2）以杆长为优化变量，将塑壳断路器的位置方程作为约束条件，以速度方程作为优化函数，采用改进的PSO 算法进行优化，该算法的运用可以快速收敛并求得优化结果。

（3）运用ADAMS 对优化前后的结构进行仿真，结果表明优化结果合理，触头旋转角度提升了约10°，分断速度提高了0.4 ms，与优化前差距不大，可通过提高主簧力减少分断时间。