基于深度迁移的有向加权网络节点重叠检测

王小红,刘 琴

(青海民族大学计算机学院,青海 西宁 810000)

1 引言

随着通信技术和互联网技术的飞速发展,有向加权作为众多网络表达形式中的一种,网络内部节点分布规律性较强,但由于众多节点的加权项一致,通过权值部署很容易出现节点重叠现象。随着节点的不断堆积,网路规模逐渐扩大,数据量不断增加,节点间的关系也越来越复杂难以分辨,分布混乱,久而久之形成更为繁杂的网络,影响运行效率。近年来,这种节点重叠现象引起了计算机、互联网以及电子信息技术等各个邻域的重视。

文献[1]提出一种基于密度峰值和社区归属度的节点重叠检测算法。利用佩奇排名算法对网络节点的影响力降序排列,挑选序列值相同的节点进行标记划分,找出相同序列值内密度值和社区归属度一致的数据节点,判定为重叠点。该方法通过降序排列、标记划分再到归属度和密度值的判定,对于数量较大的节点来说,整个过程复杂度过高、耗用较大、实用性不强;文献[2]采用粗糙粒化检测网络嵌入式重叠节点,描述网络节点结构、特征等属性,对相似性较高的节点进行空间映射,明确节点间重叠关系。该方法没有考虑到噪声干扰的问题,重叠映射的误差较大

综合上述问题,本文对有向加权网络中的节点进行分区检测,首先,利用深度迁移算法计算聚合度、分离度,获得网络重叠社区的中心度值,挑选中心度最高的数据节点作为社区中心,计算中心节点在各个社区的隶属度,归属度最高的社区即为重叠社区,根据重叠原理,该社区内一定存在重叠节点。分别对赋予重叠社区中相邻节点和节点数据边赋予不同权重,根据权重值求得重叠度。通过预先判定重叠社区可降低后续检测可能受到的外界干扰,对不同的节点都能实现精准检测。

2 基于深度迁移的有向加权网络中心节点确定

从概率论的角度来看,深度迁移是不断学习不断获取信息的过程,应用在重叠检测中,可通过上一迁移任务重叠节点信息来获取下一任务重叠节点信息。一般情况下,深度学习[3]只涉及两个域:一个是节点源域,用E={X,P(X)}表示,其中,X为节点的特征空间,P(X)表示边缘节点[4]的概率分布,X=X1,X1,…,Xm∈X;另一个为目标域,用F={X,P(X)}表示,迁移任务可以用HT表示。迁移学习的目的是在每一个迁移任务中捕捉到关键信息,通过节点源域迁移任务[5],学习预测目标域中重叠的相关知识。

在进行节点重叠检测前,需要在众多节点中挑选中心节点,最简单的选择方法就是按照节点度的排列顺序选择最大的那一个。但该方法存在过大误差,因为节点度最大节点占比权重不一定是最大的,在有向加权网络中,权重值较大的节点才是核心,与剩余节点之间存在紧密联系。通过中心点与节点之间的关联,查找重叠度较高的节点,降低误判。本文通过节点内部的分散度和聚合度两项指标,选取中心点,过程如下:

1)节点聚合度Ii:是指节点i与相邻节点之间的最大相似度[6]乘积,用于描述节点之间的聚合关系,表达形式为:

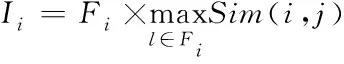
(1)

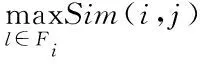
2)节点分离度[7]Ji:是指节点i与相邻节点之间最大相似度的乘积倒数,用于描述节点间的分离程度,表达形式为:

(2)

3)节点中心度Ki:是指网络节点聚合度Ii与分离度Ji数值的乘积,表达形式为

Ki=Ii×Ji

(3)

节点的中心度值Ki越大,表示成为社区中心的可能性越大。

3 包含重叠节点的重叠社区检测

在实际的有向加权网络中,由于节点会受到兴趣偏好、特征属性、区域位置、密度以及横纵向维度等多种因素的干扰,很有可能出现多个节点社区。因此,要想提高重叠节点检测的准确性,需要对网络中各个社区分别进行重叠度检测。

3.1 重叠社区隶属度计算

计算重叠社区的隶属度函数[8]mf(·),mf(·)∈[0,1]。给定一个初始社区为Aa,该社区的隶属度函数值mf(Aa)越大,代表节点属于该社区的概率越高。由于网络中各个社区内部数据存在紧密相连关系,社区外部的数据存在稀疏关系[9]。计算mf(·)与节点之间的连接关系,表达公式如下

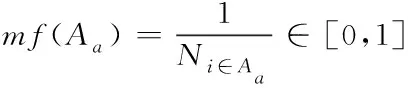
(4)

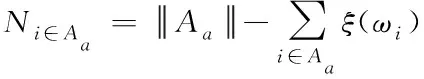
(5)

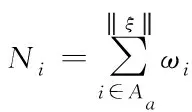
(6)

式中,Ni∈Aa表示节点i在社区Aa内相遇的个数;Aa表示社区内全部节点数量;ωi表示节点权重;ξ表示相遇次数[10]。当相遇次数ξ=0时,相遇个数Ni∈Aa=0,ξ值越大,相遇个数Ni∈Aa自然会越大,该节点属于社区的概率越高。

3.2 节点归属度计算

通过上述过程判定出节点的隶属度关系,计算待检测社区的重叠度。节点除了对自身所属的社区隶属度较高外,还可能对其它社区的隶属度也较高,出现这种现象会影响检测的精度。为了能精准检测发生重叠的社区,计算数据对每个社区的归属度值[11]emf(Aa)为

(7)

式中,emfi(Aa)表示初始社区对外部节点的归属度值,将emf(Aa)和emfi(Aa)进行比较,即可得到重叠社区为

(8)

式中,Remf(Aa),emfi(Aa)表示检测出的重叠社区节点集合;if表示社区内存在节点数据;none表示社区内不存在节点数据。

采用上述方法对有向加权网络节点社区进行重叠检测,可初步判定节点是否属于重叠社区中,在一定程度上提高了检测的精准性。

4 不同类型节点重叠检测算法

4.1 节点权重

本文通过赋予重叠社区内所有节点同等权重方式,对边缘节点和共邻节点进行重叠检测。

设权重值集合为G2=(C2,V2,B2),∀α∈C2,∀β∈V2,其中,C2表示边缘节点集合的权重值,∀α∈C2;V2表示共邻节点集合的权重值,∀β∈V2;B2表示剩余节点集合。将节点α和β的权重值定义为,与其相邻的所有节点权重和D(x),公式为

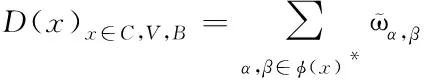
(9)

式中,α,β∈φ(x)*表示与节点相邻的所有节点集合;ϖα,β表示节点α和β的定义值。

节点的权重值可以描述检测节点周围数据的连接关系[12],以图1、2给出的有向和无向加权网络[13]为例,节点4的权重计算为:D(4)=0.7+0.5+0.6=1.8;节点6的权重计算为:D(6)=0.3+0.2+0.2+0.4=1.1。

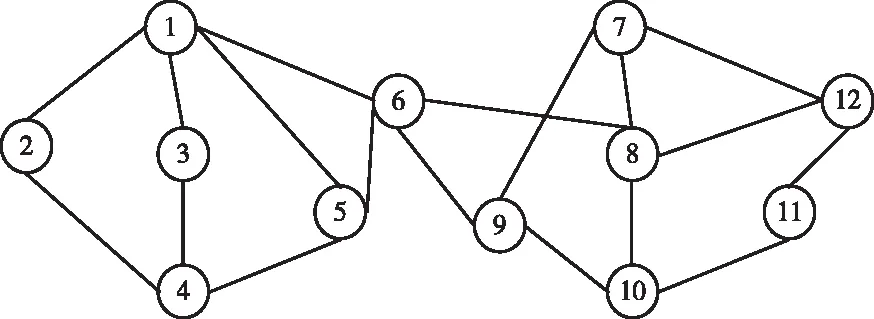
图1 无向加权网络示意

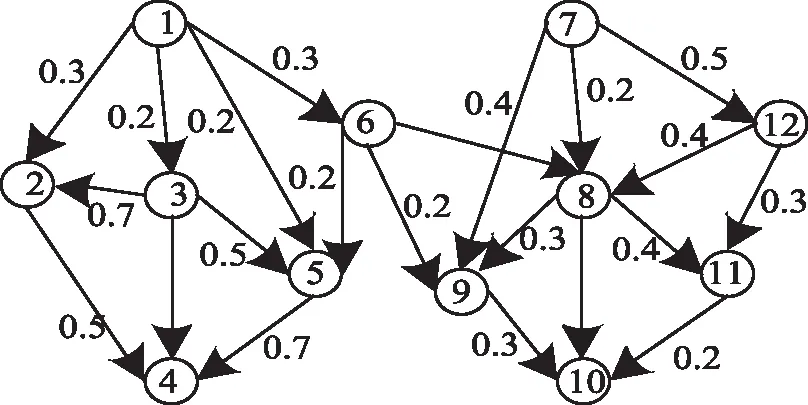
图2 有向加权网络示意

4.2 共邻节点重叠度检测

通过权重赋值概念,给定重叠社区内两个相近的点为α′、β′,用φα′、φβ′表示两个节点之间的重叠度,根据权重定义,两点之间的邻域重叠比Hφα′φβ′为

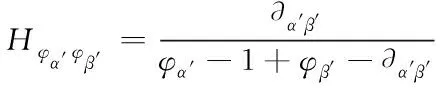
(10)

式中,∂α′β′表示相邻数量,等式分子的值越小代表相邻节点的重叠比越大,连接程度越强,重叠概率越高。

(11)

式中,ξ表示数据边的权重度量[14,15],当数据边之间存在连接时,等式值越大代表数据边之间连接的紧密度越高,反之则为越差。以这种方法取得的重叠度值,较为准确,误差小。

5 仿真研究

5.1 仿真设置

本文仿真在One NET(Opportunistic Networks Environ-ment全国物联网开放平台)上进行,该平台是由移动公司开发的Paas(Platform as a Servic物联网开放终端),具有数据覆盖面广、储存量大的优势。为了能验证本文算法对有向加权网络节点重叠检测的效果,与基于社区归属度的重叠节点检测算法、基于网络嵌入重叠节点检测算法进行对比分析。检测指标分别为:平均检出率Fd、平均负载程度FOB,其中,平均检出率Fd验证正确检测到重叠节点占全部节点的比例值;平均负载程度FOB验证算法每检测到一个重叠节点,相应付出的成本,Fd、FOB的计算公式如下

(12)

(13)

式中,Ms表示正确检测到节点的数量;MOC表示出现重叠现象节点的初始值;M2表示节点的全部数量。仿真参数如表1所示。

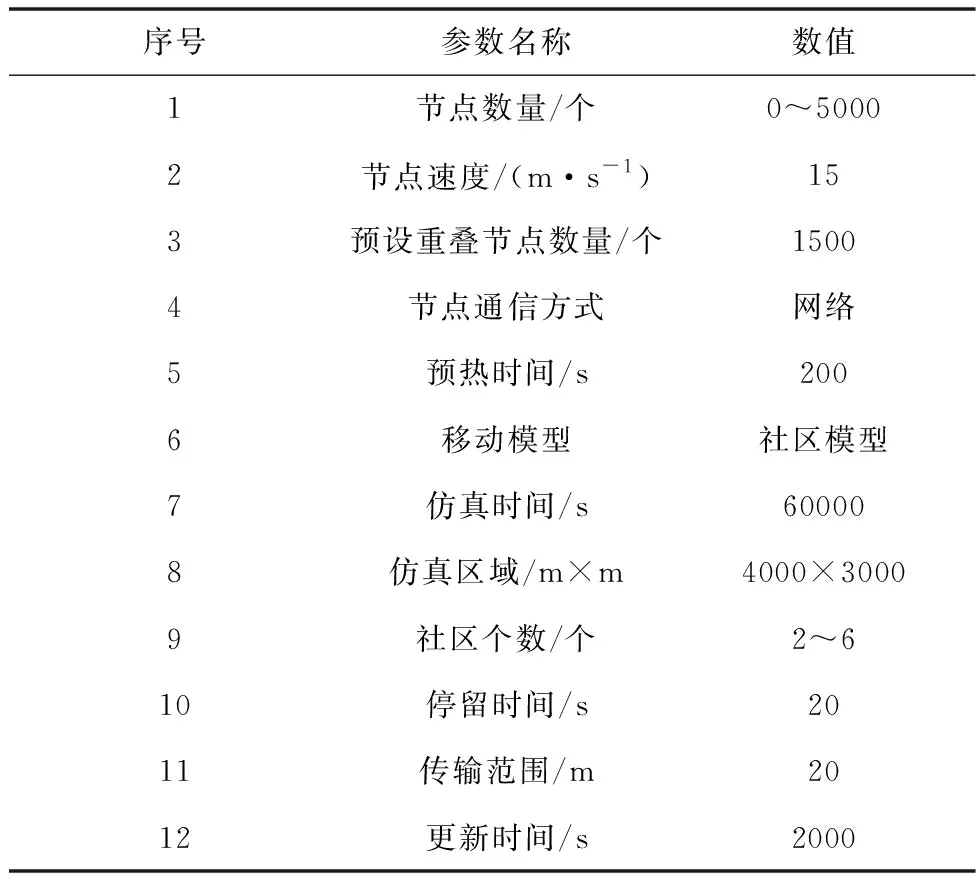
表1 仿真参数

5.2 检测效果对比

三种方法的平均检出率、平均负载程度指标测试结果如图3、4所示。

图3 平均检出率对比曲线

从图3中可以看出,随着节点数量的不断增加,所提方法的平均检测率曲线属于一种稳中略降的变化趋势,另外两种方法曲线是剧烈下降趋势。这是因为节点数量上涨打破了原本节点之间的信息串联规律,使得节点关系变得复杂,节点间的区分度变小,难以检测,导致平均检测率下降。而本文没有受到过多影响是因为,预先划分了节点的重叠社区,对社区内中心节点及边缘节点采取不同的检测手段,来降低因目标不明确或定位模糊带来的影响。

从图4中可以看出,在3000检测点,本文方法平均负载程度比传统方法要小约0.25左右,曲线的变动幅度不大。其中,基于社区归属度方法检测耗用代价过高,是因为没有深度挖掘重叠节点的信息特征,在分步检测时,不能根据节点间的特征关联快速查找到与其相关的节点,需要重复寻找耗用大;而基于网络嵌入重叠算法不能明确节点的关键特征,例如:密度、大小等,目标过于分散,误检率过高,导致需要频繁二次检测,代价成本过高,负载率上升。

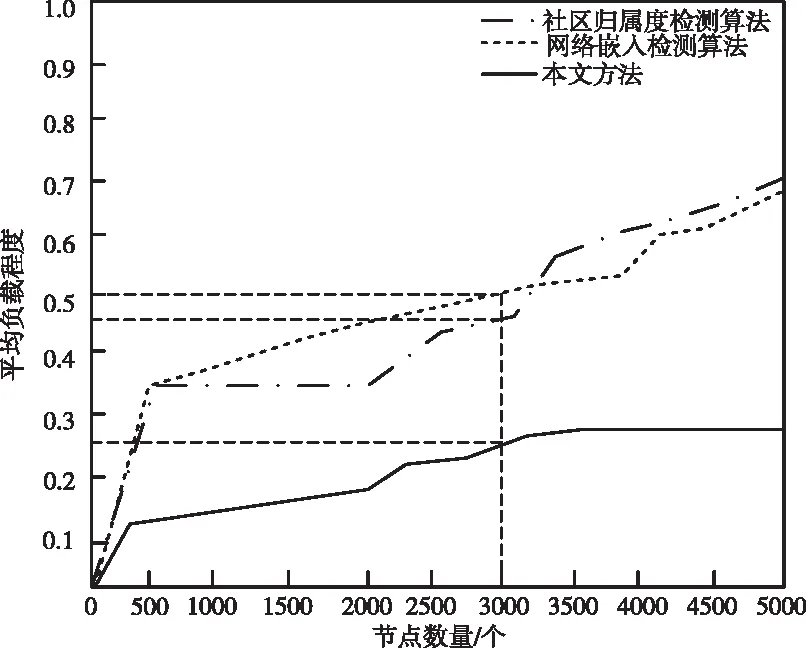
图4 平均负载程度对比曲线

5.3 检测时间对比

重叠检测时间实验结果如图5所示。

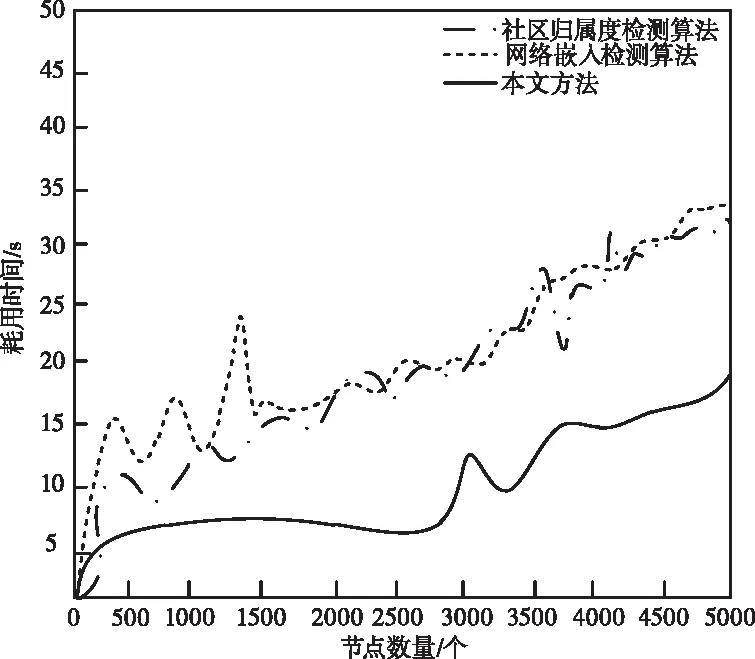
图5 算法耗用时间曲线对比

从图5中可以看出,本文算法耗用时间曲线处于较为平稳增长趋势,无论是从整体还是浮动细节变化来看都要优于另外两种方法。这是因为,本文方法对数据类型进行了详细的划分,根据数据的不同属性给出不同的重叠检测方法,做到了对应的检测,不仅可以保证检测准确性,也降低了误检的可能,没有额外的时间耗用;而另外两种方法采用的检测模式较为单一,不预先对数据划分,直接从整体出发进行重叠检测,初始检测的时间耗用相对较少,但由于单一的模型存在过多误差,导致误检率及漏检率高,需要重新检测计算,反倒增加了时间耗用。

6 结论

实现重叠节点的精准检测对提高有向加权网络运行效率具有非常重要的作用,本文提出了结合深度迁移学习的检测算法。通过节点聚合度和节点分离度得到社区中的中心节点,利用中心节点关联度较高的特性,求得与其隶属度最高的社区,判定社区为重叠社区。采用重叠度权重计算法得到相邻节点和边缘节点的重叠度,完成精准检测。相比普通算法,所提方法对不同节点实现了对应检测,一步步获取节点之间的关键连接关系,检测精度高,时间耗用量小,逻辑表达明确,计算步骤简单易实现。