基于群体智能算法的混合属性大数据聚类仿真

古险峰,汤永利

(1. 郑州工业应用技术学院信息工程学院,河南 郑州 451100;2. 河南理工大学计算机科学与技术学院,河南 焦作454000)

1 引言

如何在大量的数据中找到需要的数据类别,提高数据的利用价值已成为当前网络应用的巨大挑战[1]。聚类分析能够将数据集划分成众多类别,在增加同簇对象相似度的同时,尽可能地减小不同簇对象的相似度[2]。目前有很多聚类方法,但因数据具有数值属性和分类属性,大多数的聚类方法只能对单一类型的数据进行处理。如果采用单一型处理的方法对数据进行聚类,会严重影响混合数据的聚类效果,导致数据中重要的信息丢失[3-5]。

由于生活中存在的数据大部分都是具有数值属性与分类属性的混合属性数据,因此混合属性的数据是广泛存在的,对混合属性数据进行聚类研究具有重要意义。文献[6]在混合属性数据聚类中引入了聚类融合算法,通过聚类融合理论求解数据的聚类问题,把每类属性作为一个聚类器的输出,构建出算法的框架,并建立了最大化共享信息的目标函数,该方法大大提高了测试数据与客户管理数据的稳定性与准确性。文献[7]设计了由网络爬虫、数据处理和数据分析等四部分模块组成的硬件系统,分别通过单机与分布式方法对大数据进行聚类处理,并在设计的硬件平台上编写数据处理与数据分析的程序,该方法对混合属性的数据分析准确性较高。文献[8]在自监督学习群体智能算法中引入突变操作,优化最优解,同时计算出各个样本的行为方程,采用K-means方法提高算法的收敛速度,该方法聚类质量较高,收敛速度较快。

针对混合属性数据聚类质量不高的问题,对数据集中的数据点所包含的数值属性和分类属性进行分析,对数据集中的随机数据点间的距离度量做响应处理。利用信息熵确定数值属性数据中的权重值,计算出类中心的相似度,并对粒子群算法进行改进。通过对真实数据集的仿真,验证基于群体智能混合属性数据聚类方法的有效性。

2 混合属性数据聚类

针对混合属性数据的聚类问题,主要有类型转换、聚类融合、层次聚类和密度聚类等几种方法,后两种方法与数值属性聚类方法思路相似,均将混合属性数据点的距离度量与传统聚类思路进行综合分析处理,因此本文将混合属性数据的相似性作为重点的度量方法进行研究。

聚类融合方法是混合属性聚类的主要方法之一,主要思想是通过对一种算法进行多次运算或通过多种算法对一组对象进行划分,并利用共识函数对得出的结果进行合并聚类处理。假设混合属性数据集为X,每个数据对象为Xi,对数据集X按照a维属性相似度进行聚类分析,将数据集a维属性映射到一维分类属性,该分类属性用矩阵可表示为

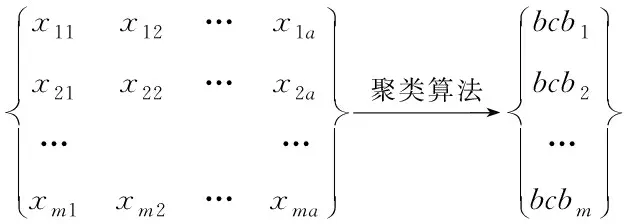
(1)

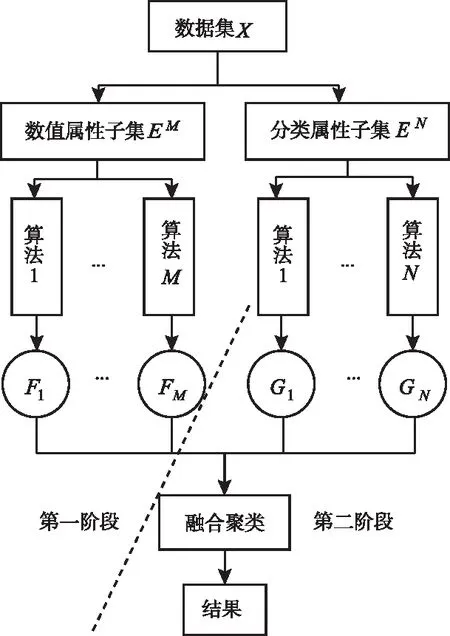
图1 混合属性数据分段融合聚类框架

采用混合属性数据分段融合框架不仅提高了对分类属性子集的处理效率,还降低了信息的失真性。针对特定属性值域,构建相似属性值集合,该集合中任意值在集合中贡献的距离用公式可表示为

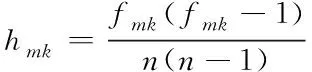
(2)

其中,fmk表示属性值在值域中出现的频率;n表示数据集中数据的点数;k表示数据维度。那么任意两个数据点(Xi,Xj)的距离用公式可表示为

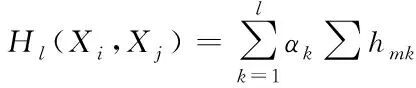
(3)

其中,l表示两个数据点(Xi,Xj)的共有维度;αk表示第k维分类属性的熵权比值系数。在高维度下,通过设定相似度阈值β,来判断两个数据点是否在该维度上相等。每一维度数据点和簇的概率相似度称为点簇相似度,用公式可表示为

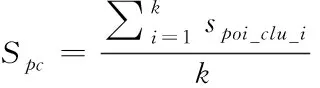
(4)

其中,spoi＿clu＿i表示第i维度上的点簇维度概率相似度;k表示数据点的维度。为了更好地体现数值属性数据聚类效果,利用信息熵对数值属性数据加权处理,可以避免类中心数据一致导致的空簇问题。信息熵直接反映数据的有用程度,信息熵越小,表明数据集越有序;信息熵越大,表明数据集越杂乱。第s维属性的信息熵用公式可表示为

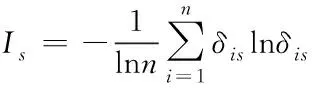
(5)

其中,δis表示数据对象Xi的第s维数据属性比重;n表示数据对象的个数。信息熵的权值用公式可表示为

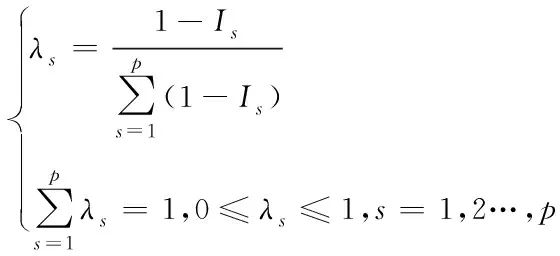
(6)

为了克服数据集中任意两个数据点选择初始聚类中心造成聚类结果不稳定的问题,采用平均差异度方法选择每个数据对象的初始聚类中心。中心思想是:数据集中数据的初始聚类中心平均差异度应该较大,且聚类中心的差异度要比数据集的总体平均差异度大。平均差异度和总体平均差异度用公式分别表示为

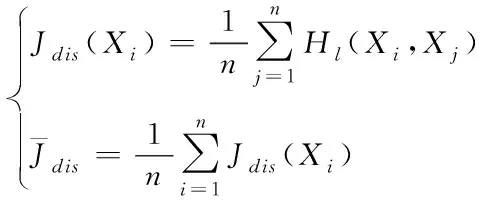
(7)

通过混合属性距离及平均差异度的计算,在传统方法的基础上扩展了对数值属性数据处理的限定,能够更好得解决混合属性数据的聚类问题。

3 群体智能算法

群体智能优化算法采用并行搜索方式解决初始聚类中心敏感问题,将聚类分析作为优化问题解的一种算法。群体智能算法具有无集中控制点和组织能力强等特点,本文主要从数据的编码方式、评价指标数等方面入手,对群体智能算法进行优化。

3.1 编码方式

群体智能算法的优化主要是对数据集的目标函数和编码方式进行考虑。针对聚类问题,编码方式不同,对应的目标函数也不同,因此确定数据的编码方式非常必要。

将数据点按顺序进行标号1～N,那么聚类中心的搜索空间可表示为[1,N],选择搜索空间中的m个数据点作为聚类中心{Y1,Y2,…,Ym},编码结构如图2所示。

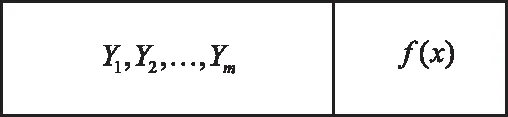
图2 编码结构

通过对待分类数据样本的聚类中心进行编码,可以确定出可行域的范围为[1,N],个体位置是可行域范围内数据集中数据点的组合,由于数据点的映射范围是明确的,因此能够大大提高搜索效率,减少群体智能算法中无效解的产生。

3.2 评价指标

为了衡量聚类问题的有效性,需要根据聚类结果的形态评价聚类效果,采用适应度函数对个体的好坏进行评价。根据聚类中心与聚类方法求出适应度函数,最常见的适应度函数为聚类误差,聚类误差平方用公式可表示为:

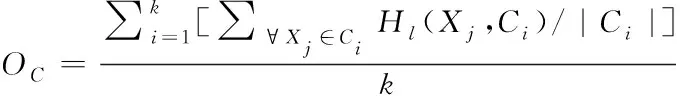
(8)

其中,k表示聚类个数;Hl(Xj,Cj)表示数据点与聚类中心间的距离;|Ci|表示分类到第i类数据点的数目。按照本文方式进行实数编码时,通过数据集的数据间相异度矩阵描述,聚类的适应度函数表示为

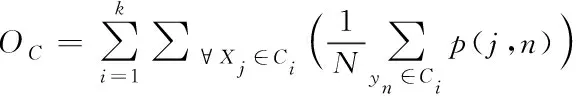
(9)

其中,yi表示第i个聚类中心;p(j,n)表示数据点Xi和Xj的相异度值;N表示样本总量。

3.3 改进粒子群算法聚类

为了解决聚类中心敏感、数据易陷入误区等问题,利用粒子群智能优化算法的全局搜索能力找到数据集中的最优解,将聚类问题视为解的优化问题。

粒子群聚类算法通过对粒子个体位置的不断更新,来寻找全局最优解。每个粒子不仅能够记住搜索过程的最优解,还能记住整个粒子群的最优位置。假设每个粒子的速度为V,维度和个体位置为Q,那么粒子在下一时刻的速度用公式表示为:

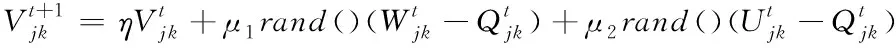
(10)

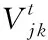
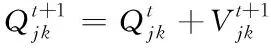
(11)

为了提高算法的速度,对粒子群算法进行改进。具体步骤为:

Step1:对待分类数据样本的聚类中心进行编码,对粒子群初始化,保证速度为相同维度。

Step2:根据相异度计算出适应度值。

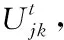
Step4:迭代终止,重复Step2和Step3。

Step5:将聚类结果输出、评价。

设种群的粒子数目为M,那么每次迭代后粒子的更新位置用公式可表示为:

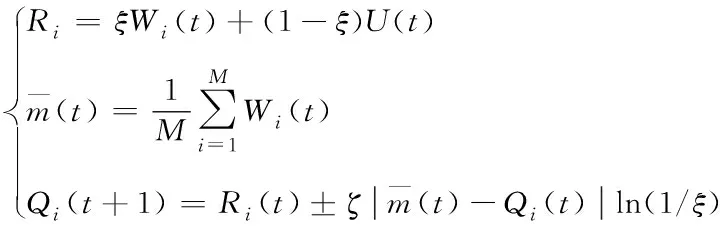
(12)

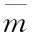
4 仿真与结果分析

为了评估分段融合聚类框架和改进群体智能算法的有效性与可行性,实验在MATLAB仿真平台上实现,实验数据选取UCI数据库中的Iris、Creditapproval、Heartdisease和Soybean具有代表性的4个数据集,这4个数据集中有3种数据类型,分别为数值型数据、混合型数据和分类型数据。数据集的描述如表1所示。

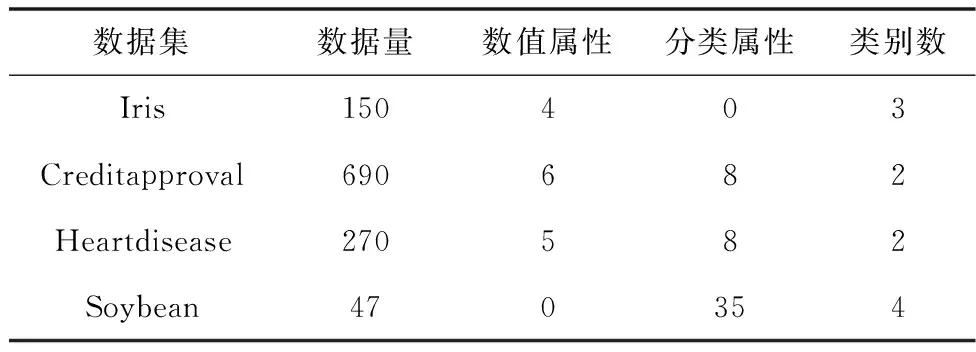
表1 数据集描述

为了对聚类质量进行评估,采用的评价指标为聚类准确率,公式可表示为

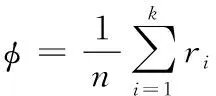
(13)

其中,n表示数据集总量;ri表示数据集被正确分类的数据点数量;k表示聚类数量。分别将本文方法与文献[6]、文献[7]和文献[8]的方法进行对比,实验结果如图3所示。

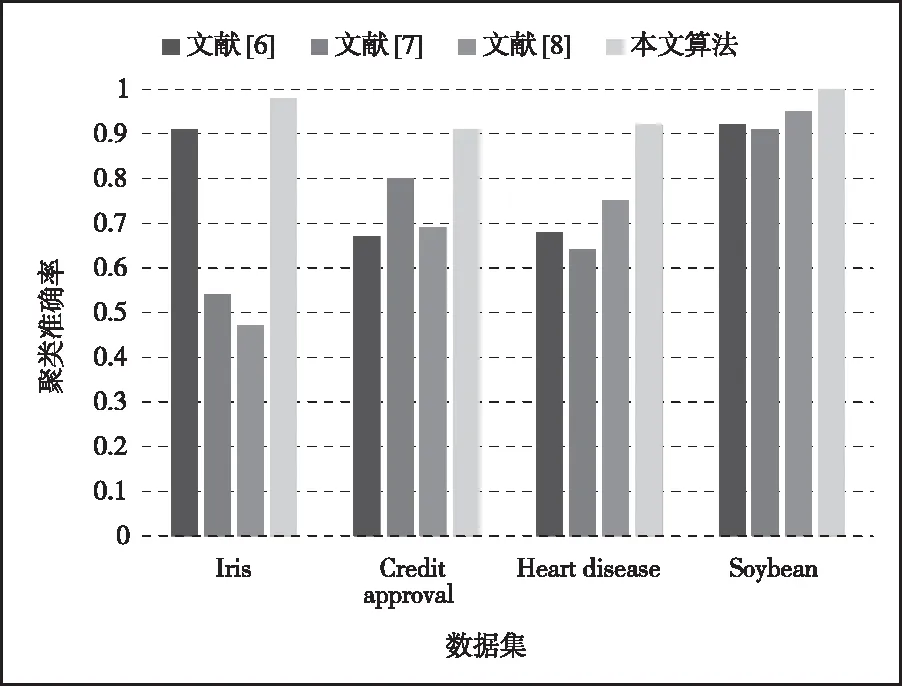
图3 聚类准确率对比结果

从图中可以看出,采用本文算法对数据集进行聚类分析,无论是处理数值型数据、分类型数据,还是混合型数据,聚类准确率均高于其它算法,说明本文算法的聚类质量较高。

为了进一步对数据的聚类质量进行验证,比较本文算法与文献[6]、文献[7]和文献[8]的方法的聚类精度,结合Creditapproval数据集的聚类结果,对数据集依次进行迭代,比较不同算法的目标函数值,对比结果如图4所示。

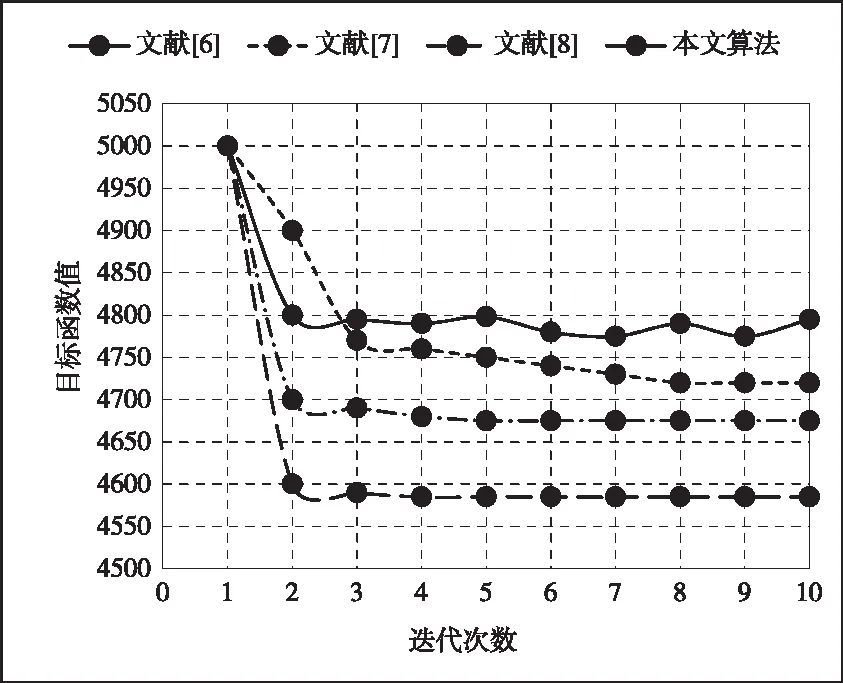
图4 目标函数值对比结果

从图中可以看出,当迭代次数为1时,采用这4种方法,目标函数值均有降低趋势,然而采用文献[6]方法的下降趋势不明显,随着迭代次数的增加,采用文献[7]方法的目标函数值不稳定,在相同情况下,很明显本文算法的目标函数值小于其它算法,说明本文算法的聚类精度比其它方法都高。

为了验证编码方式与适应度函数对聚类问题的影响程度,将本文方法与粒子群算法进行比较,总体精度对比结果如表2所示。

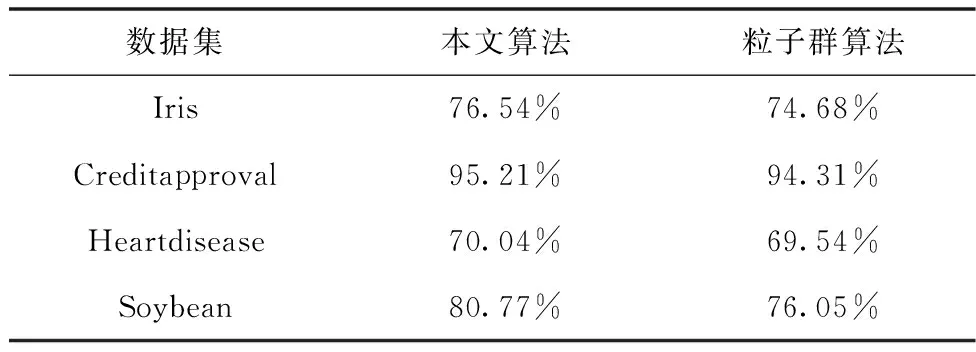
表2 总体精度对比结果

从表中可以看出,改进的粒子群算法具有较高的总体精度,聚类效果良好。改进的粒子群算法采用本文的编码方式,在一定范围内可以限定住粒子的搜索,解决了粒子算法搜索超出空间,产生无效解的问题。本文算法不仅提高了搜索效率,还增强了算法的鲁棒性,大大降低了算法的复杂度。

5 结束语

由于实际生活中产生大量的数据,且大多数都是由数值属性和分类属性构成的混合属性数据,为了对混合属性数据的聚类进行研究,提出基于群体智能算法的混合属性大数据聚类方法。

对初始聚类中心的选取方法进行优化,并对混合属性的数据度量方法进行改进,使数据集中的数据点在划分过程中可以更加准确的与各种聚类集的相似度进行区分,并对群体智能优化算法进行分析与改进。选取UCI数据库中具有代表性的4个数据集,在MATLAB平台上实现仿真,实验结果表明,本文算法的聚类质量和聚类精度均高于其它算法,验证了本文算法的有效性与可行性。