改进人工势场法机器人避障路径规划研究

高飞翔,郝万君,吴 宇,孙 诚

(1. 苏州科技大学电子与信息工程学院,江苏 苏州 215009;2. 苏州科技大学物理科学与技术学院,江苏 苏州 215009)

1 引言

随着人工智能的快速发展,机器人技术得到进一步开发,具有各种功能的机器人开始逐渐融入到日常生活中[1]。机器人工作时都需要进行路径规划,路径规划分为全局路径规划和局部路径规划,它可以为机器人在各种复杂环境中规划一条安全、快速的路径。常用的路径规划算法有:蚁群算法(Ant Colony Optimization,ACO)、遗传算法(Genetic Algorithm,GA)、快速搜索随机树法(Rapid-Exploration Random Tree,RRT)和人工势场法(Artificial Potential Field,APF)等[1]。

APF法不同于其它的路径规划智能算法,APF是基于局部路径规划的智能算法,运用在路径规划中需要根据当前机器人的位姿以及距离障碍物的距离来规划下一步动作,其算法本身具有计算量小、算法反应速度快、生成路径顺滑等优点[1]。徐小强[4]等人提出从安全距离概念避免多余路径,引入预测距离解决目标不可达问题,在机器人陷入局部极小值时利用虚拟障碍点逃离局部极小点,但是未曾考虑复杂障碍物下机器人是否可以完整规划路线。何乃峰[5]等人提出利用模拟退火算法重建APF函数模型,重新规划全局路径,虽然避免了局部极小值但是所规划的路径不是全局最优路径。吴宇[6]等人提出的利用A*与DWA算法进行融合优化,提出自适应参数融合改进算法,在栅格地图中可以有效避开障碍物建立安全且平滑的行进路线,但是这种方法的计算量大,运行缓慢,收敛精度低。杨周[7]等人提出的利用ACO与DWA算法融合,但融合的算法在面对复杂环境问题时,区域搜索最佳转折点不完整可能会导致可行区域的收敛性低,从而影响整个路径规划的完整性。

针对以上TAPF应用于路径规划存在的弊端,提出了利用自适应切线偏转角确定虚拟障碍点的APF算法,改进斥力函数引入机器人与目标点的动态影响距离以及调节因子系数,避免遇到目标不可达问题,利用当前机器人行径位置提出自适应切线偏转角法,以最远障碍物为参照物在另一侧确定虚拟障碍点,通过引入虚拟斥力解决振荡易陷入局部最小值问题,使得机器人可以更快、平稳的到达目标点。然后通过MATLAB仿真验证该算法的正确性,并进行了实际论证。

2 APF算法

2.1 地图构建

ROS智能机器人进行路径规划前利用激光雷达对周围复杂环境进行数据扫描,将扫描到的数据建立模拟地图模型。本文利用栅格地图进行复杂环境的搭建模拟,栅格地图具有简洁的特点,可以直观的显示出仿真结果,在众多路径规划仿真中得到广泛应用。

本文采用如图1所示栅格地图进行复杂环境复现,黑色栅格表示障碍物,白色部分表示无障碍物可以通过区域。

图1 栅格地图

2.2 APF算法基本原理

APF是路径规划中应用较广泛的智能算法之一,最早由Khatib在80年代提出[4]。在APF算法中,整个机器人运动过程比作一颗运动粒子在带有正负极的电势场中运动的过程。将整个复杂的地图环境看作一个虚拟电势场,将机器人当作电势场正极,目标点当作电势场负极,障碍物视为正极,机器人利用与障碍物引起的斥力场以及与目标点产生的引力场的合力使得机器人有效地绕过障碍物最终到达目标点。

假设机器人在二维空间中的受力情况如图2所示,且设机器人在二维空间内的位置表示为j=(x,y),目标点位置表示为jobj=(xT,yT),障碍物的位置表示为jobs=(xo,yo)。

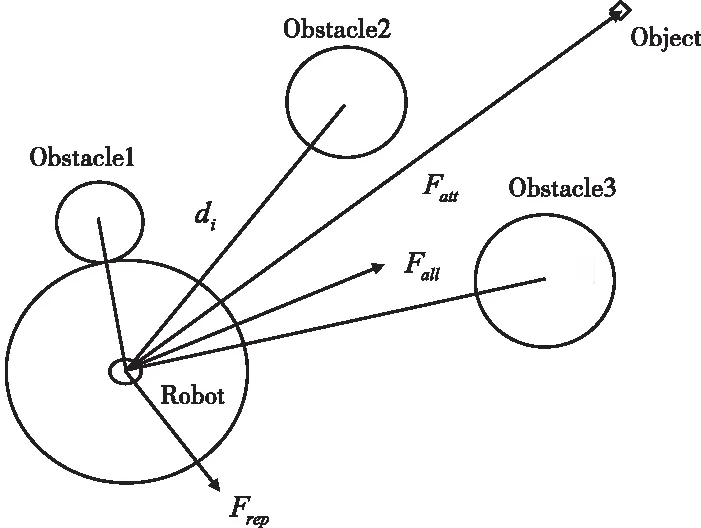
图2 传统APF受力分析

设定目标点对机器人产生的引力场表示为Uatt(j),障碍物对机器人产生的斥力场表示为Urep(j),即机器人最终受到的合力场U(j),则合力如式(1)所示:

U(j)=Uatt(j)+Urep(j)

(1)

其中,引力场函数如式(2)所示:

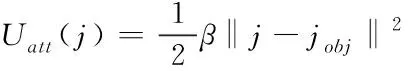
(2)

式中,β为引力势场增益常数,β>0;‖j-jobj‖为机器人当前位置与目标点的距离。机器人与障碍物之间的斥力势场函数如式(3)所示

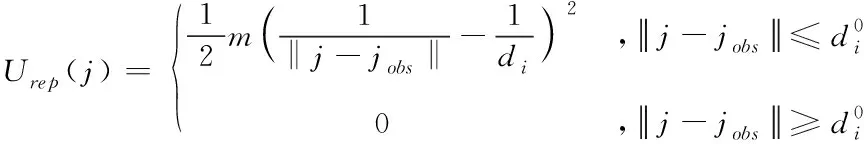
(3)

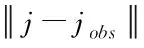
势场力为负梯度时,机器人受到的势场引力如式(4)所示

Fatt(j)=-∇Uatt(j)=β(jobj-j)

(4)

机器人受到的势场斥力如式(5)所示

Frep(j)=-∇Uatt(j)=

(5)

则机器人受到的合力如式(6)所示

(6)

2.3 APF法的缺陷

TAPF法不同于其它智能算法,不需要进行全局路径规划找出全局关键节点,因此其行进路线都是利用障碍物斥力及目标点引力的合力来推动机器人前进。一旦途中没有受到力的驱使或力达到平衡状态时,就会出现以下问题:

1)由于力的不平衡才驱使机器人可以向目标点移动,一旦行径策略中存在某点使其达到合力平衡的效果,机器人会产生目标不可达现象,如图3所示。

图3 传统APF目标不可达

2)机器人行进策略位于两个障碍物夹缝之中或遇到L型等复杂障碍物时,极易陷入徘徊抖动造成振荡状态,如图4所示。

图4 传统APF“振荡”

3 改进TAPF算法

3.1 改进斥力场函数

针对机器人在TAPF存在合力平衡导致目标不可达现象,引入机器人与目标点之间的动态影响距离参数,在每个障碍物斥力范围之内,将其代入斥力场函数式

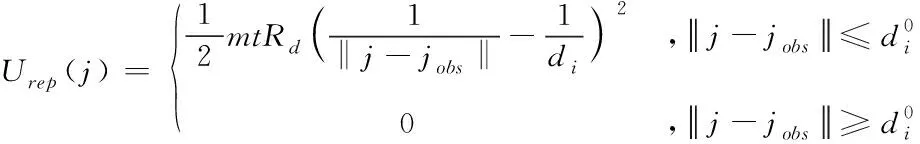
(7)

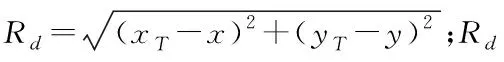
(8)

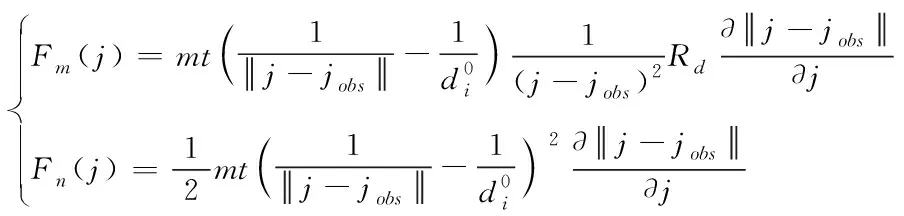
(9)

其中,Fm(j)表示机器人朝向与障碍物相反,Fn(j)表示机器人朝向与障碍物同向。

考虑改进的改进斥力函数打破力的平衡,因此引入协调力Fx,其定义为

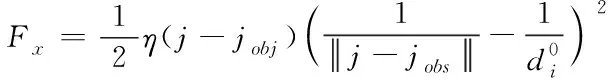
(10)

式中,η为协调系数,η的取值范围在0≤η≤1,一般取值0.5。由此,改进后人工势场合力函数为

(11)

3.2 虚拟障碍点

在机器人行进策略中,遇到L型等障碍物或在障碍物中间穿行会出现振荡情况,机器人就陷入死锁。本文提出利用自适应偏转角根据障碍物的分布情况引入额外虚拟障碍点,当机器人陷入振荡情况时,利用虚拟障碍点提供的斥力使其合力发生改变推动机器人向目标点移动。在接下来行进过程中再遇此情况,重复进行以上操作,直到机器人到达目标点为止。

3.2 自适应切线偏转角

当机器人在进行过程中遇到复杂结构障碍物时,例如U型障碍物、L型障碍物,机器人会产生振荡状态即陷入局部最小值中。当机器人处于振荡状态时,以机器人当前位置为切点,做当前振荡轨迹的切线l1,如图5所示;以当前切线为基准线建立坐标轴;再以机器人为圆心,距离机器人受到斥力最远障碍物距离Ri为半径顺时针做圆;机器人与最远障碍物之间的距离为dis(Robot,Obsm),利用式(12)计算得出自适应切线l1的偏转角ζ的大小,将切线l1顺时针旋转偏转角ζ得直线l2与圆相交得两点γ1与γ2;将最远障碍物另一侧的为设定的虚拟障碍点Obsset,如图6所示。

图5 轨迹切线示意图

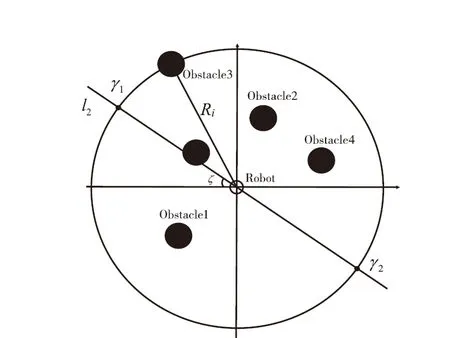
图6 设定模拟障碍点示意图

自适应切线偏转角ζ可表示为

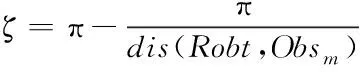
(12)

4 改进APF算法流程

本文改进传统APF避障算法,解决传统APF在做局部路径规划时遇到的目标不可达以及振荡现象。其具体步骤如下:

步骤 1:初始化栅格地图及算法参数。

步骤2:确定栅格地图中机器人的初始位置及机器人的目标点。

步骤3:利用传统APF法计算机器人在行进过程中每一步的斥力场及引力场。

步骤4:通过机器人周围的障碍物计算出斥力与目标点对其的引力得出合力,判断合力是否为零,进而判断是否遇到传统APF法的两大问题之一,使用改进型斥力场函数,寻找新的局部路径;通过机器人判断,对于仿真中出现振荡状态从而陷入局部最小值问题时,利用自适应偏转角ζ找出位于最远障碍物另一侧的虚拟障碍点,添加额外斥力使得机器人摆脱局部最小值。

步骤5:通过APF法计算下一时刻机器人前进位置,最终抵达终点,如再遇上述问题返回步骤4重新找寻新的下一步路径。

改进融合算法的机器人路径规划流程图,如图7所示。

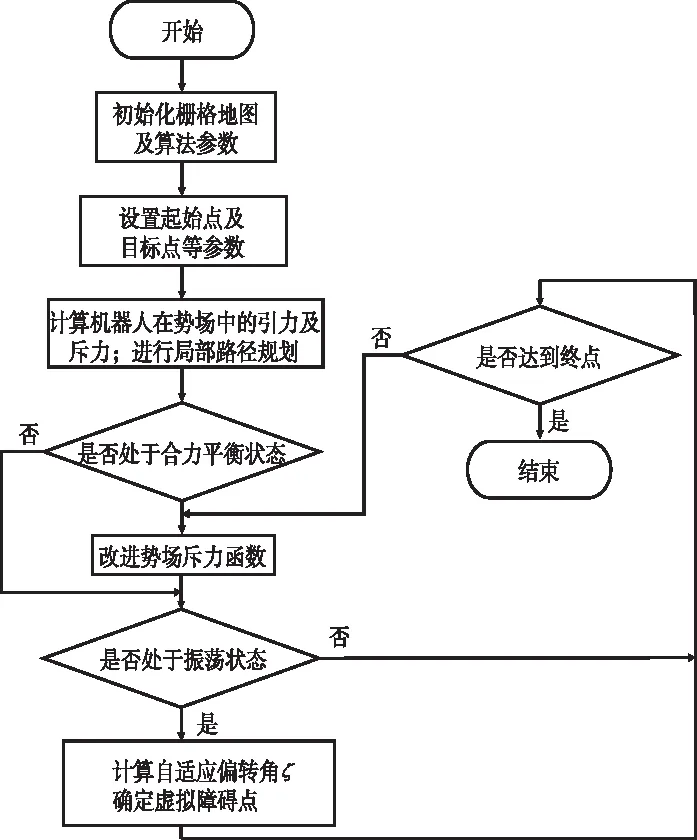
图7 改进APF算法的机器人避障示意图

5 仿真及结果分析

为验证本文所提算法的可行性以及普适性,利用MATLAB2016a仿真平台分别在20×20、25×25、30×30三种大小的栅格地图下进行改进后避障算法仿真。

将本文所提的改进APF算法与TAPF算法以及文献[4]所提A-APF算法分别在三种大小的地图中进行对比实验。将移动机器人视为一个质点,黑色矩形代表栅格地图中的障碍物,绿色正三角S表示起点,红色正三角T表示目标点。主要设置参数如表(1)所示,环境一、二、三中障碍率分别为0.075、0.136、0.1444,如图8-图10所示。

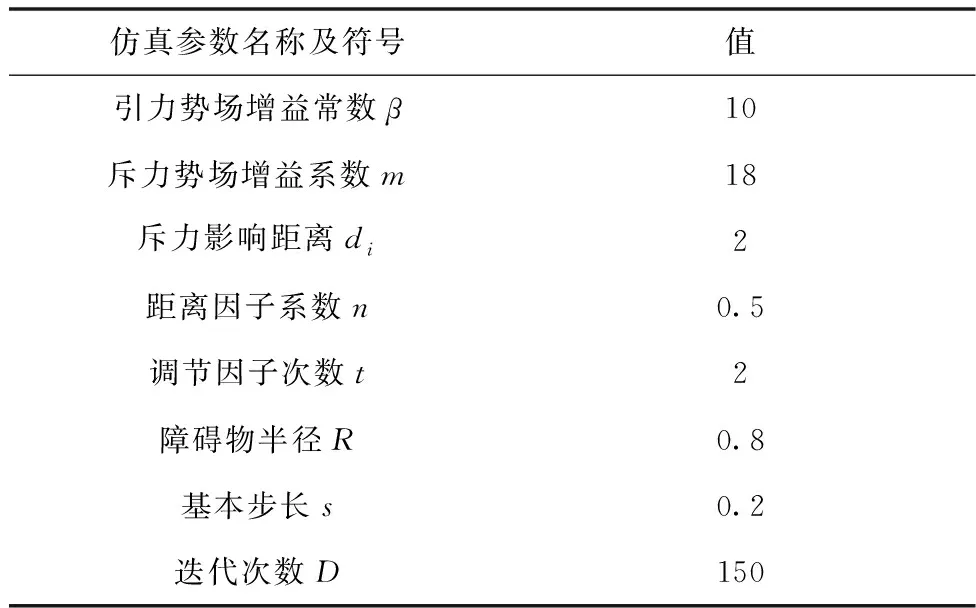
表1 仿真参数设定

图8 环境一下三种算法的路径规划图

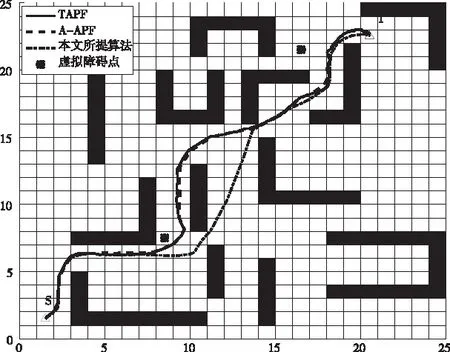
图9 环境二下三种算法的路径规划图

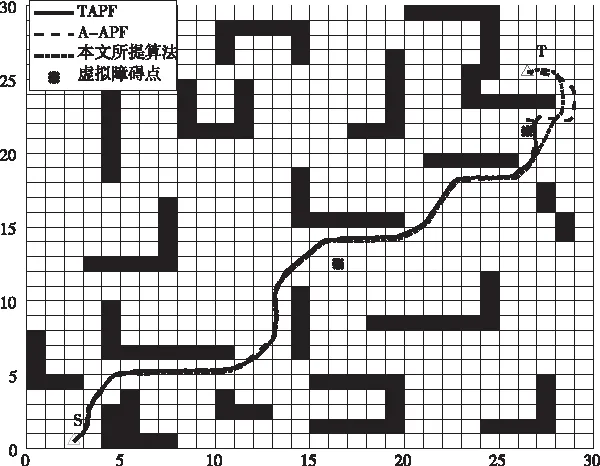
图10 环境三下三种算法的路径规划图

从图8-图10可以看出,在不同障碍率和不同尺寸的环境下,TAPF算法面对复杂障碍物通常会在行进途中陷入局部极小值从而走入死胡同,A-APF算法提出虚拟目标点方法以及本文所提利用自适应切线角所确定虚拟障碍点算法均能规划出完整路径。如表2-4所示,给出三种环境下,三种不同算法的性能参数。从表2-4可以看出:

表2 20×20复杂环境地图中仿真数据

表3 25×25复杂环境地图中仿真数据

表4 30×30复杂环境地图中仿真数据

在20×20的栅格地图环境中,TAPF算法由于复杂障碍物存在陷入局部极小值,无法规划完整路线,而本文算法较A-APF算法在步长、时间方面分别降低了14.2%、13.1%;

在25×25的栅格地图环境中,TAPF算法规划出完整路线,但振荡频率较大,而本文算法较TAPF及A-APF算法在步长、时间方面分别降低了34.2%、26.3%,20.6%、15.8%;

在30×30的栅格地图环境中,TAPF算法因复杂障碍物无法规划出完整路线,而本文算法较A-APF算法在步长、时间方面分别降低了9.6%、12.5%;相同仿真环境下,利用TAPF、本文所提算法对TAPF算法所存在两个缺陷进行对比仿真,如图11、图12所示。

图11 TAP目标不可达情况及改进

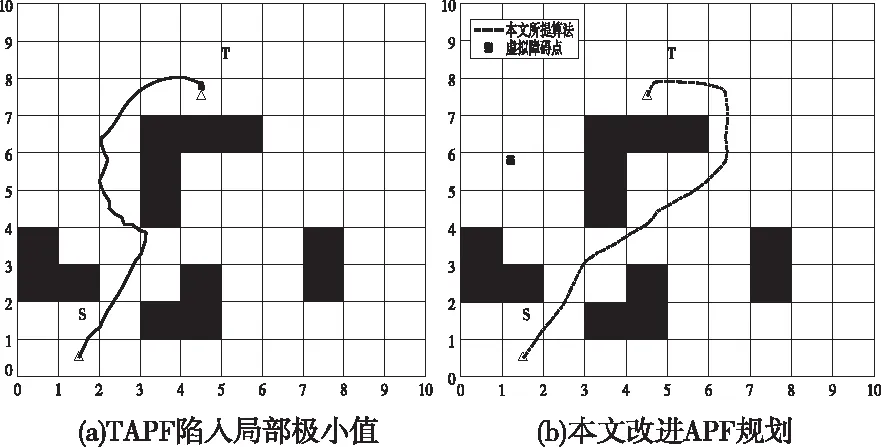
图12 TAPF陷入局部极小值情况及改进

如图11所示,TAPF面对合力为零导致目标不可达就此算法进入死胡同,本文所提算法改进斥力场函数引入动态距离影响参数以及斥力场调节因子,避开了合力为零的状态;如图12所示,面对复杂障碍物例如L型障碍物等,TAPF会陷入局部极小值出现振荡现象,TAPF又会进入死胡同,本文改进后的算法提出自适应切线偏转角,确定合适的虚拟障碍点,从而使得机器人摆脱局部极小值,顺利到达目标点。

通过上述分析可以看出本文所提算法与TAPF、A-APF算法在路径长度、时间都有较大的优化;在路径长度方面与A-APF算法相差不多,但本文所提算法的时间以及平滑度与A-APF算法相比有明显提高。综上分析,本文所提改进TAPF避障算法有进一步的改进,路径更平滑,拐点更少,通过不同大小环境对比而言更加具有普适性。

6 实际论证

为了验证在实际环境中本文所提算法的有效性以及可靠性,将本文所提改进TAPF避障算法应用到图13(a)中的轮式激光雷达机器人中,进行实物论证。利用激光雷达对周围环境进行数据扫描,如图13(b)所示。

图13 实际验证环境

如图14所示,为实验验证过程图。黑色方框为轮式智能机器人,粉红色为实际障碍物,红色线为智能机器人局部路径规划路线。

图14 轮式机器人行进策略轨迹图

起点为图中红绿交叉直角处,设置好后,智能机器人向目标点移动,通过激光雷达扫描到障碍物时,通过改进算法可以成功避开障碍物,继续向目标点前进。规避障碍物轨迹如图14(a)-图14(d)所示,通过图15(a)、图15(b)可以看出规划局部路线时能够与障碍物保持一定的安全距离并且避障轨迹较为平滑,符合机器人实际运行动力学特点。

图15 轮式机器人实际避障图

7 结论

1)针对TPF算法目标不可达情况,本文对其传统斥力场函数进行改进,引入机器人与目标点之间影响距离以及障碍物斥力场调节因子,通过仿真与TAPF和文献[4]所提算法A-APF进行对比,本文优化算法路径更加平滑,用时更少。

2)针对复杂环境下TAPF会出现振荡陷入死区现象,本文提出自适应偏转角确定虚拟障碍点,通过额外斥力使得机器人摆脱局部极小值,继续向目标点前进直到到达目标点。

3)本文利用ROS轮式智能机器人进行算法实际测试,测试结果显示,在复杂环境下机器人也能够安全,快速的进行障碍物避障直到抵达设定目标点。

综上,本文所提避障算法能够为智能机器人行进策略规划好安全路线,为智能驾驶提供一定的行进决策借鉴意义。