翻筋斗的改进麻雀搜索算法
欧阳城添,黄祖威,朱东林,闫少强
(1. 江西理工大学信息工程学院,江西 赣州 341000;2. 火箭军工程大学作战保障学院,陕西 西安 710038)
1 引言
随着优化问题的复杂度不断提升,群智能算法应用愈加广泛,尤其在工程领域上表现突出。麻雀搜索算法(Sparrow search algorithm,SSA)是Xue和Shen[1]于2020年提出的新型群智能优化算法。作者抽象了麻雀群体的觅食和反捕食行为,以食物位置为待求解,模拟麻雀觅食过程来寻找最优解。该算法原理简单,种群角色与参数较少,且鲁棒性强,在函数优化方面比传统的粒子群算法(Particle Swarm Optimization,PSO)[2]和灰狼算法(Grey Wolf Optimizer,GWO)[3]的精度更高,寻优能力更强。在麻雀搜索算法提出后,它也被应用于工程领域中,例如提出者薛建凯[4]已经成功地将其与无人机航迹规划结合,并取得良好成效。但SSA也有一些弊端,比如易陷入局部最优和依赖初始化种群等问题。
为改进麻雀搜索算法存在的缺陷,吕鑫等[5]提出了混沌麻雀搜索算法。通过引入基于随机变量的Tent映射、混沌扰动及高斯变异机制等策略,丰富种群多样性,防止算法陷入局部最优,加强了算法的全局搜索能力。吕鑫等[6]还提出基于改进麻雀搜索算法(ISSA)的多阈值图像分割法。通过引入鸟群算法的思想,来加速算法收敛,提高算法的搜索能力。毛清华等[7]提出一种融合柯西变异和反向学习的改进麻雀搜索算法,利用一种折叠次数无限的sin混沌机制初始化种群,引入自适应权重策略协调局部搜索与全局搜索,再采用融合柯西变异和反向学习策略在最优位置上进行扰动变异,产生质量更高的新解,增强算法跳出局部最优的能力。Liu等[8]同样引入混沌策略增加种群的多样性,并使用自适应惯性权重平衡算法的收敛速度与探索能力,最后采用柯西-高斯突变策略来摆脱后期算法停滞的限制。Zhang等[9]采用logistic映射、自适应参数和变异算子等策略,增强SSA的全局搜索能力。Liang等[10]在SSA中融入均匀混沌、自适应惯性权重等策略,还对算法中的边界约束作出改进,增添种群多样性,一定程度上提升了算法的全局搜索能力。
虽然关于麻雀搜索算法的改进策略不断提出,但每种策略的提出没有明显改变麻雀搜索算法自身的寻优机制,仅在邻域空间内提高算法的搜索能力,没有动态调节算法的寻优能力,导致算法仍有缺陷。例如,常见的混沌映射虽然能提高种群的多样性,使种群分布均匀,但存在不确定性,没有一定的学习能力。针对这些不足,本文提出翻筋斗的改进麻雀搜索算法(SISSA)。在算法初期采用Tent映射和反向学习初始化种群,具有一定的学习选择能力,为算法寻优提供充分的准备;之后将非线性收敛因子融入发现者的位置更新中,增强发现者的探索能力,再引入翻筋斗策略使追随者的位置更新具有灵活性,使得算法寻优方式更加细致,提高算法的局部搜索能力;最后利用两个历史最优解的差分结果找到可靠的解。通过12个标准测试函数将SISSA与其它6种算法进行对比,证明了SISSA具有高效的寻优能力,且在Wilcoxon统计检验上得到了有效的验证。将SISSA和三种算法应用于机器人路径规划,通过比较观察得出,SISSA在实际应用中也有更好的效果。
2 翻筋斗的改进麻雀搜索算法
2.1 麻雀搜索算法
麻雀种群有两种角色,分别是发现者和追随者,它们有觅食、跟随、侦察三种行为。发现者具有良好的全局搜索能力,带领其它个体找到最优食物的位置,发现者的位置更新公式如下
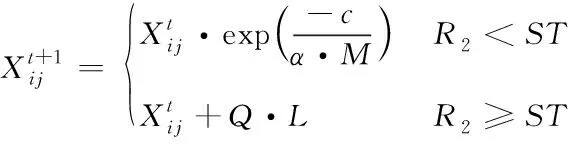
(1)
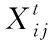
追随者跟随发现者进行觅食,这一行为相当于局部搜索,适应度较好的个体优先获得食物。追随者的位置更新公式如下
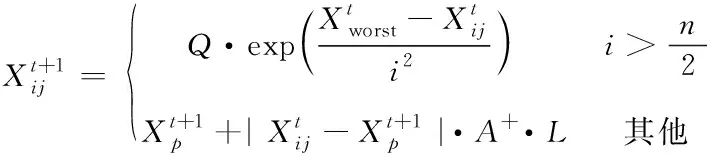
(2)
麻雀种群中存在负责侦察的个体,发现危险时会发出警报,从而提醒发现者带领其它个体前往安全区域。具体行为公式
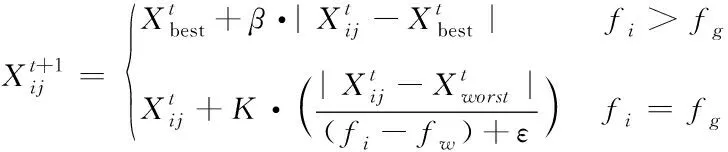
(3)
2.2 Tent映射反向学习初始化种群
在群智能优化算法中,初始化种群至关重要。其主要目的是为个体寻优提供充分的准备与良好的寻优空间,使种群分布密度较高,加快算法的寻优速度。但多数初始化种群策略具有不确定性等因素,例如多种混沌映射理论,初始化过程没有绝对的完整及均匀性。为使得种群个体更加可控,本文采用Tent映射和反向学习对种群进行初始化。Tent映射在均匀性及遍历性较其它映射具有优势[11,12],所以采用Tent映射初始化麻雀群体,并采用反向学习策略[13,14]对初始种群进行提炼,筛选出更加优秀的麻雀个体,为算法寻优提供良好的环境,从而提升算法的收敛速度。Tent映射的表达式为
(4)

Tent映射反向学习初始化种群总共分为三步:
1)使用Tent映射产生的混沌序列初始化麻雀种群的位置xij(i=1,2…D,j=1,2…N),N表示种群数量;
3)将两种方式产生的个体位置按照适应度高低排序,选取适应度排名前N个的个体作为最终的初始种群。
2.3 非线性收敛因子
发现者作为种群的领导者,需要广泛细致的搜索机制。非线性收敛能够平衡局部搜索与全局搜索能力,与自适应收敛因子相比具有更高的可信度,因此本文采用如下公式更新发现者的位置
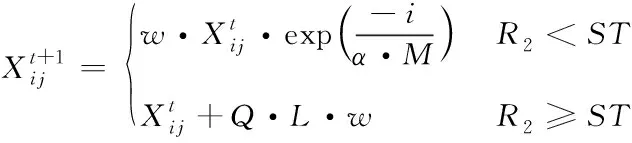
(5)

(6)
2.4 翻筋斗策略
麻雀搜索过程中,追随者会紧随发现者进行搜索,这种搜索方式单调,且范围较窄,容易出现早熟现象。传统的反向学习策略虽能提升种群多样性,但其只能在平行空间内找到反向解,算法的灵敏度不佳。针对此问题,本文采用翻筋斗觅食策略[15]来解决。翻筋斗策略在搜索方式上更加多样,通过此策略更新追随者位置,灵活搜索可靠解,以此提升SSA跳出局部最优的能力。翻筋斗策略是以当前最优为中心点,每次更新位置都位于当前位置与其关于中心点对称的位置连线之间。位置更新公式如下
i=1,2….N
(7)
式(7)中,S代表空翻因子,本文将S取值为2,目的是使每次位置更新都能在当前位置与对称位置之间;r1,r2是区间[0,1]中的随机数。翻筋斗策略示意图如图1所示。
2.5 局部搜索
每当个体找到当前最优解时,如果遇到局部极值就会使算法寻优能力受阻。设麻雀搜索算法寻优过程中P1与P2分别为种群历史最优解及种群历史次代最优解。本文采取两解的差分指导P1进行搜索,找到邻域内可靠的最优解。具体实现方式如下:
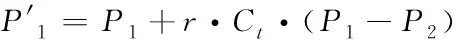
(8)

(9)

(10)
其中,fit(x)为x的适应度值。
2.6 翻筋斗的改进麻雀搜索算法
综合上述策略,本文提出一种翻筋斗麻雀搜索算法。算法初始阶段采用Tent混沌映射反向学习初始化种群,搜索阶段采用非线性收敛因子改善发现者的搜索范围,再引入翻筋斗策略使追随者的搜索更具有灵活性,避免出现早熟现象,最后通过两个历史最优解的差分进行局部搜索,并更新邻域内质量更优质的解,从而加快算法的寻优速度。具体伪代码如下:
算法流程
Input
M:最大迭代次数
PD:发现者
SD:意识到危险的麻雀个体
R2:预警值
N:麻雀总体数量
Output:Xbest,fg
采用Tent映射反向学习初始化种群
t=1;
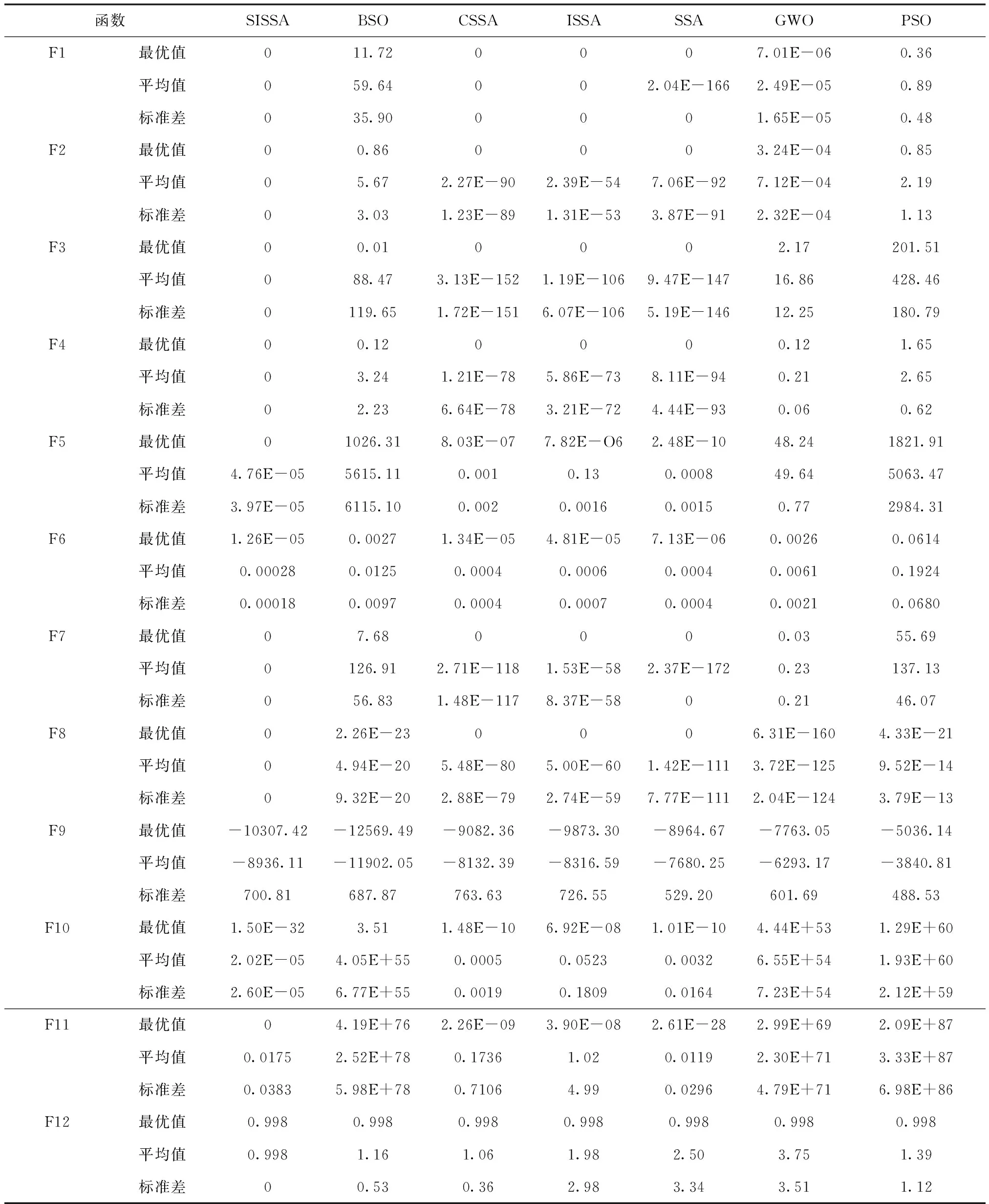
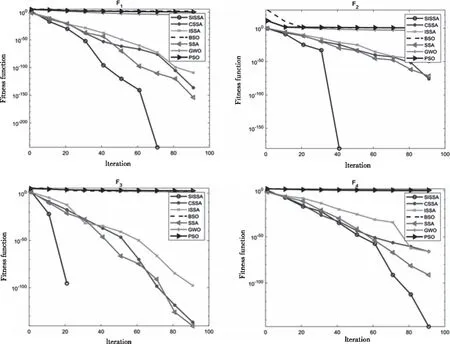
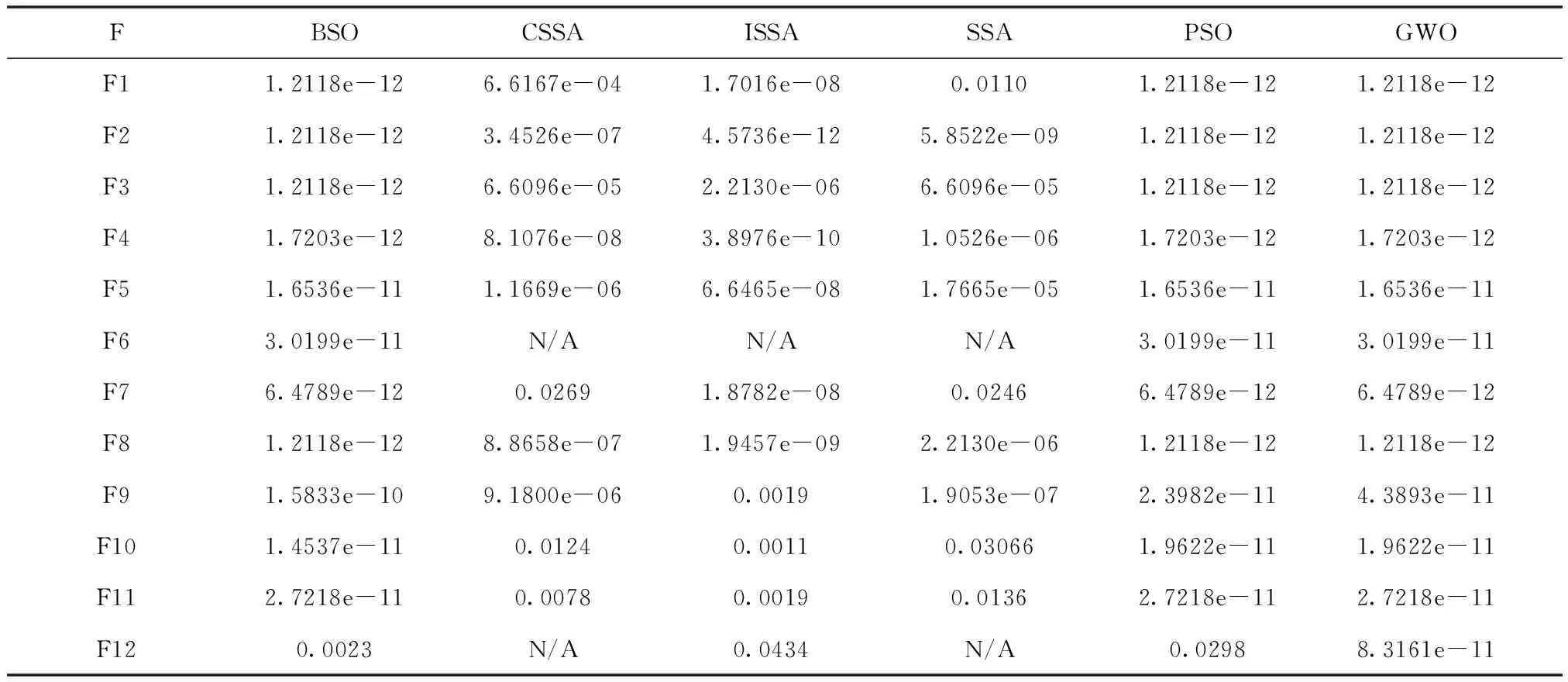
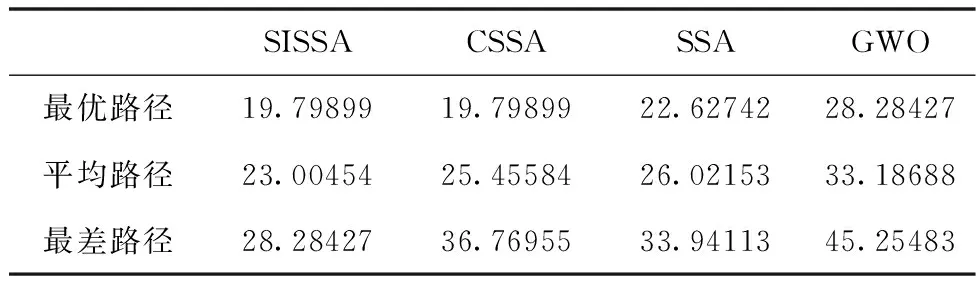
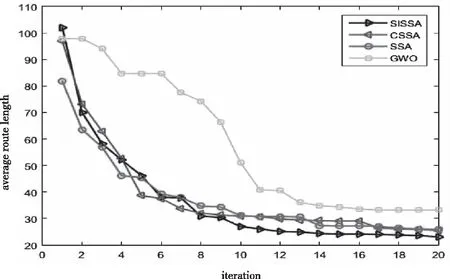
While(t 根据适应度值找到最优及最差麻雀个体的位置。 R2=rand(1) For i=1:PD 根据式(5)(6)更新发现者的位置; End for For i=(PD+1):N 根据式(2)和(7)更新追随者的位置 End for For i=1:SD 根据式(3)意识到危险的麻雀个体位置 End for 得到新的最优个体的位置 根据式(8)-(10)更新最优个体的位置 t=t+1 End while Return:Xbest,fg 时间复杂度是衡量算法质量的重要指标。从宏观上来看,设算法的种群规模为P,最大迭代次数为M,问题的维度为D,SSA与其它智能优化算法一样,时间复杂度为O(P×M×D),而SISSA仅在初始化阶段增加了时间复杂度为O(P)的反向学习策略,对整个算法寻优而言,并没有时间增量,因此增加的O(P)可以忽略不计。 从微观上来看,设追随者的比例为r,计算反向解的时间为t1,计算最优的前20个体的时间忽略不计,引入翻筋斗策略的位置更新计算时间为t2,最优解的局部搜索的计算时间为t3,且Tent映射初始化与原算法时间复杂度相同。从算法伪代码可以看出,SISSA算法在初始化阶段增加了O(P*(t1)),在追随者位置更新阶段增加了O(M×r×P×t2),在最优解更新阶段增加了O(M×t3),可见SISSA较SSA增加了O(P×(t1)+M×r×P×t2+M×t3),但在数量级上并没有提升,且能使算法的寻优效率与精度有效地提高,所以时间复杂度的些许增加有积极意义。 为了检验 SISSA的性能,选取表1 中的 12个标准测试函数进行测试,其中包括复杂单峰测试函数 F1-F8 和复杂多峰测试函数F9-F11,F10及F11是来自于CEC2017中的复杂函数,其边界范围较广,F12为固定维度的复杂函数。具体测试函数信息如表1 所示。 表1 测试函数信息表 将SISSA与CSSA,ISSA,BSO,SSA,PSO,GWO各算法进行对比,BSO[16]是近几年研究比较热门的融合算法。为保证算法的公平性,所有的仿真在 CPU 为 Intel(R) Core(TM) i5-10200H,主频为 2.40GHz,内存为16 GB 的 PC 上,采用 MATLAB R2019a实现。参数设置与各文献中参数设置保持一致,种群规模为100,最大迭代次数100,PSO两个学习因子c1=c2=1.4962;权重w=0.729;BSO与文献[16]保持一致;每个算法独立运行 30 次,统计各算法运行结果的最优值,平均值,标准差三项指标,衡量算法的寻优性能及稳定性。实验结果如表2。由表2可看出,SISSA具有较强的寻优能力,尤其是在F5及F11中,只有SISSA找到理论最优值,其它算法的寻优效果基本落后于SISSA;在复杂边界问题中,PSO、BSO与GWO表现较差,不适用此类问题。综上可说明,SISSA在打破了原算法寻优机制的束缚,存在一个合理的寻优手段。 表2 各算法寻优效果对比表 为更好的体现SISSA较强的收敛能力,图2展现出了各算法在12个函数上的收敛对比图。如图2所示,SISSA具有较强的收敛能力,在单峰函数上具有较快的收敛速度,尤其在F1-F4和F7-F8中,收敛速度和精度与其它算法相比具有较大优势;在多峰函数上具有较好收敛精度,仅在F9中稍微落后于BSO,且与其它算法相比具有更好的跳出局部最优能力;在固定维函数中,SISSA的优化效果总体来看也较有优势,证明SISSA的有更强的局部搜索和全局搜索能力。综上所述,多策略的SISSA算法在函数优化上具有更加优秀的表现,证明其函数优化能力更强。 图2 各算法寻优轨迹图 仅凭三项指标确定改进算法的性能具有片面性,为体现其合理性及公平性,通过统计检验对改进算法相比于其它算法的优越性进行评估。本文采用Wilcoxon秩检验显示每个算法的是否存在显著性差异,在5%的显著水平下进行试验,当P<0.05时,可认为拒绝零假设,即存在显著性差异;P>0.05时,则表明两算法之间的差异性不明显,则用N/A表示。 由表3可看出,改进的算法SISSA仅在F6函数上与其它算法差异不明显,剩余函数上均具有显著性的差异。由此可见,SISSA较其它算法具有更高的精度,进一步验证了SISSA的有效性。 表3 Wilcoxon秩和检验P值 为了进一步验证SISSA的实用性与可靠性,本文将其运用到机器人路径规划的仿真当中。 机器人路径规划本质上就是对于给定的起点与终点,通过算法决定躲避障碍的策略,选择出一条最佳路径。这里采用栅格化[17]的方法来模拟机器人路径规划的环境。栅格化法用l×l个小方格代替真实环境,并且每一个小方格的值为0或1,1代表障碍物,0表示可通行。此方法不仅有效地简化了路径规划的环境创建过程,还能够更便捷地观察算法路径规划的效果。 SISSA应用于机器人路径规划仿真时,每只麻雀代表着一条可行路径,每只麻雀位置的维度D由栅格数l决定。根据适应度值选择路径,适应度值计算公式如下 (11) 其中,j是麻雀个体的第j个维度。 实验通过与CSSA、SSA、GWO在15×15的栅格环境下作对比来验证SISSA的可行性。设置种群数量为50,迭代次数为20,其它实验参数与上述实验一致。每个算法执行15次以消除偶然性。 各算法的最优路径如图3所示。本实验采用三个指标——最佳路径、平均路径和最差路径来衡量各算法的稳定性和可行性。各算法的优化统计表如表4,平均路线收敛图如图4。 表4 各算法优化路径统计表 图3 各算法最短路径规划图 图4 各算法的平均路径收敛图 如图3所示,SISSA规划出的路径最简单、最清晰,其次是CSSA,而SSA和GWO从它们绕行的路径能明显发现陷入了局部最优。由表4可以看出,SISSA的最佳路径和平均路径在四种算法中最小,并且其最佳路径和最差路径的差距最小,这展现出了SISSA良好的搜索能力和稳定性。从图4中可以看出,GWO的收敛性不足,收敛速度慢且不稳定;SSA及其改进算法都表现出良好的性能,收敛速度快;总体来说,SISSA的表现最好。由此可见,多策略的SISSA算法在搜索时更加灵活,大大提高了算法的搜索能力,在路径规划上表现优异。 针对新提出的麻雀搜索算法的不足,本文提出了翻筋斗的改进麻雀搜索算法,采用Tent映射反向学习初始化种群,使算法具有判断选择能力,为麻雀寻优提供良好的空间;提出非线性收敛因子使得发现者的位置更新质量更高;引入翻筋斗策略更新追随者的位置,使其更新方式更加灵活细致,最后通过两个历史最优解的差分进行局部搜索,使算法找到的解的质量得到有效的提升。在12个标准测试函数与其它算法的寻优能力进行对比,证实了SISSA的寻优效果,同时在Wilcoxon秩和检验中进一步验证了SISSA的有效性。通过对机器人路径规划的仿真,验证了SISSA的可行性和实用性。SISSA规划的路径清晰,代价函数最小。可以看出,多策略的引入有效地提高了基本麻雀搜索算法的优化能力。但SISSA算法在个别函数上存在稳定性不足情况,如何减小每次寻优结果的差异性是接下来的工作重点。2.7 时间复杂度分析
3 实验测试与分析

4 仿真结果与分析
4.1 机器人路径规划
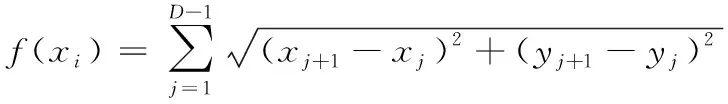
4.2 仿真环境设置
4.3 实验结果与分析

5 结束语

