求解TSP问题的改进融合遗传灰狼优化算法

刘海龙,雷 斌,王菀莹,柴 获

(1. 兰州交通大学机电技术研究所,甘肃 兰州 730070;2. 兰州交通大学交通运输学院,甘肃 兰州 730070)

1 引言

旅行商问题(Travelling Salesman Problem,TSP)是组合优化问题的典型代表之一,在现实工程问题中,许多优化问题可建立TSP模型,其中包括交通工程、电子信息、物流工程等领域,因此TSP问题长期以来是研究的热点之一。

目前求解TSP问题的算法主要分为两大类:精确算法和启发式算法。由于在现实工程问题存在维度参差不齐、实时性要求强等因素,对算法的稳定性、效率、准确性等方面均有要求,因此相较于求解效率低的精确算法,启发式算法能在较短时间内得到符合需要的可行解,更适用于现实工程问题。

多年来各国研究人员根据TSP问题的特性对不同启发式算法进行了改进与应用,Yanlan Deng[1]等人提出了模拟退火混合细胞遗传算法进行求解,Absalom El-Shamir Ezugwu[2]等人提出了融合模拟退火的共生生物搜索优化算法,余丽[3]等人提出了遗传禁忌搜索算法,陈科胜[4]等人提出了自适应升温模拟退火算法进行求解。

求解效率与求解精度是启发式算法在求解TSP问题上存在的主要矛盾之一[5],控制精度与效率的平衡是目前TSP问题算法设计的核心之一。鉴于此,本文利用遗传算法优秀的全局寻优能力和改进后灰狼算法较强的局部搜索能力来对TSP问题进行求解,并通过TSPLIB数据库的标准算例,从稳定性、精度、收敛速度、效率等几个方面对比了几种现有的的TSP求解算法进行了验证分析,以期获得更好的TSP问题求解方案。

2 灰狼优化算法

灰狼算法(Grey Wolf Optimizer,GWO),在2014年首次由澳大利亚学者 Seyedali Mirjalili等人提出[6]。灰狼优化算法因其前期收敛速度快、参数少、易实现等特点,提出的初期被广泛应用求解连续优化问题[7],近些年,经过许多研究者的探究与改进,GWO在多目标优化[8]、参数优化[9]、复杂函数优化[10]以及其它多种领域问题中的使用也越来越广泛。

灰狼群体捕食过程中会严格遵循一种等级制度,等级从高到低分别为α、β、δ和ω,狼群在α、β狼的带领下经过跟踪、包围、攻击三个步骤,最终达到捕获猎物的目的。

灰狼算法则通过模拟这种等级制度,将每次迭代产生的候选解划分为对应等级,其中当前种群最优解为α狼,次优解是β狼,第三优解为δ,其余均为ω狼,而猎物则代表全局最优解。

在狩猎过程中,α、β、δ狼对狼群下达指令,ω狼会根据α、β、δ狼发出的指令来调整自身的位置,以此达到跟踪的目的。

在GWO中,将灰狼包围猎物的行为定义如下

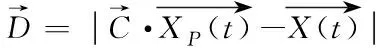
(1)

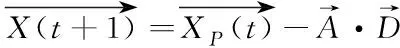
(2)

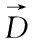
(3)

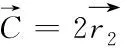
(4)

(5)

灰狼攻击猎物的行为定义如下

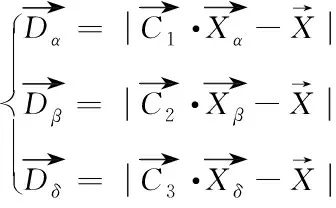
(6)

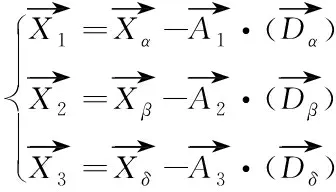
(7)

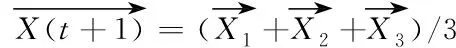
(8)

3 灰狼优化算法的改进与应用

3.1 改进的灰狼优化算法的

3.2 改进的融合遗传灰狼优化算法(GA-IGWO)

在将GWO用于求解TSP问题时发现,原始灰狼优化算法前期收敛速度快,但其全局搜索能力差,后期容易陷入局部最优或迭代停滞的现象。另一方面,根据式(8)可知,猎物的位置根据α、β、δ的指令确定,而灰狼种群位置则会根据指令判断猎物的位置进行更新,导致原始灰狼优化算法在后期开发过程中容易陷入局部最优、稳定性差等问题,因此初始解种群的优劣对于后续种群的更新也有着相当大的影响,选择合适的初始种群对于GWO的求解精度也是关键因素之一。

首先利用遗传算法(Genetic Algorithm,GA)全局搜索能力强的特点[16],对初步筛选优秀个体生成初始灰狼种群,然后利用距离启发因子将α、β、δ的指令划分权重,对原始GWO的更新策略进行改进。

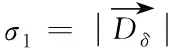
(9)

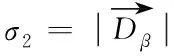
(10)

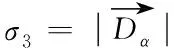
(11)

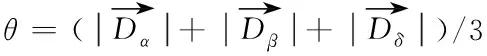
(12)

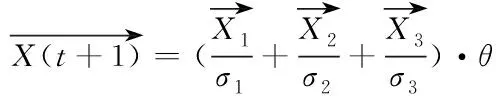
(13)

3.3 GA-IGWO算法流程

GA-IGWO算法流程见图1。

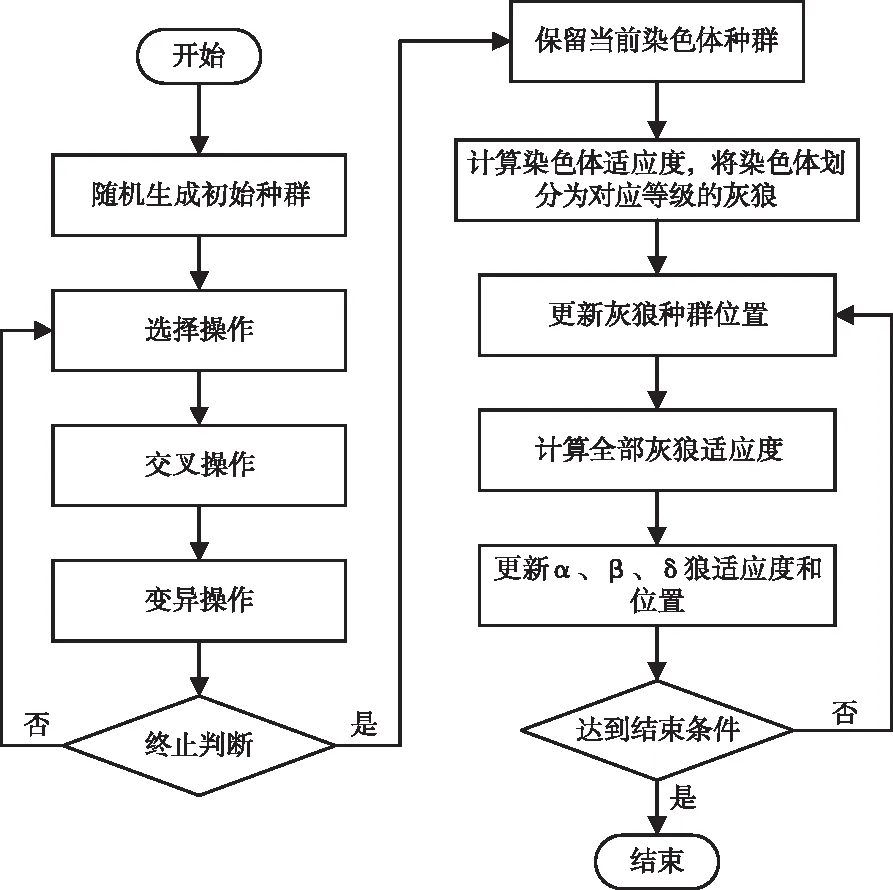
图1 改进融合遗传灰狼优化算法流程图

4 仿真分析

本实验统一在MATLAB仿真软件内进行,软件版本为2017b,计算机配置Intel(R) Core(TM) i7-9750H CPU @ 2.59 GHz,内存8.00GB,从TSPLIB数据库中随机抽取8组算例进行测试,结果将每种算法连续执行30次后所得最优解、平均值、标准差以及平均所用时间进行对比,结果保留之小数点后四位。

为验证算法的有效性,将GA-IGWO与原始GWO以及文献[11]提出的mGWO、文献[8]提出的IGWO、文献[13]提出的wdGWO、文献[14]提出I-GWO进行仿真对比,初始种群均为100,迭代次数均为100,仿真结果见表1。

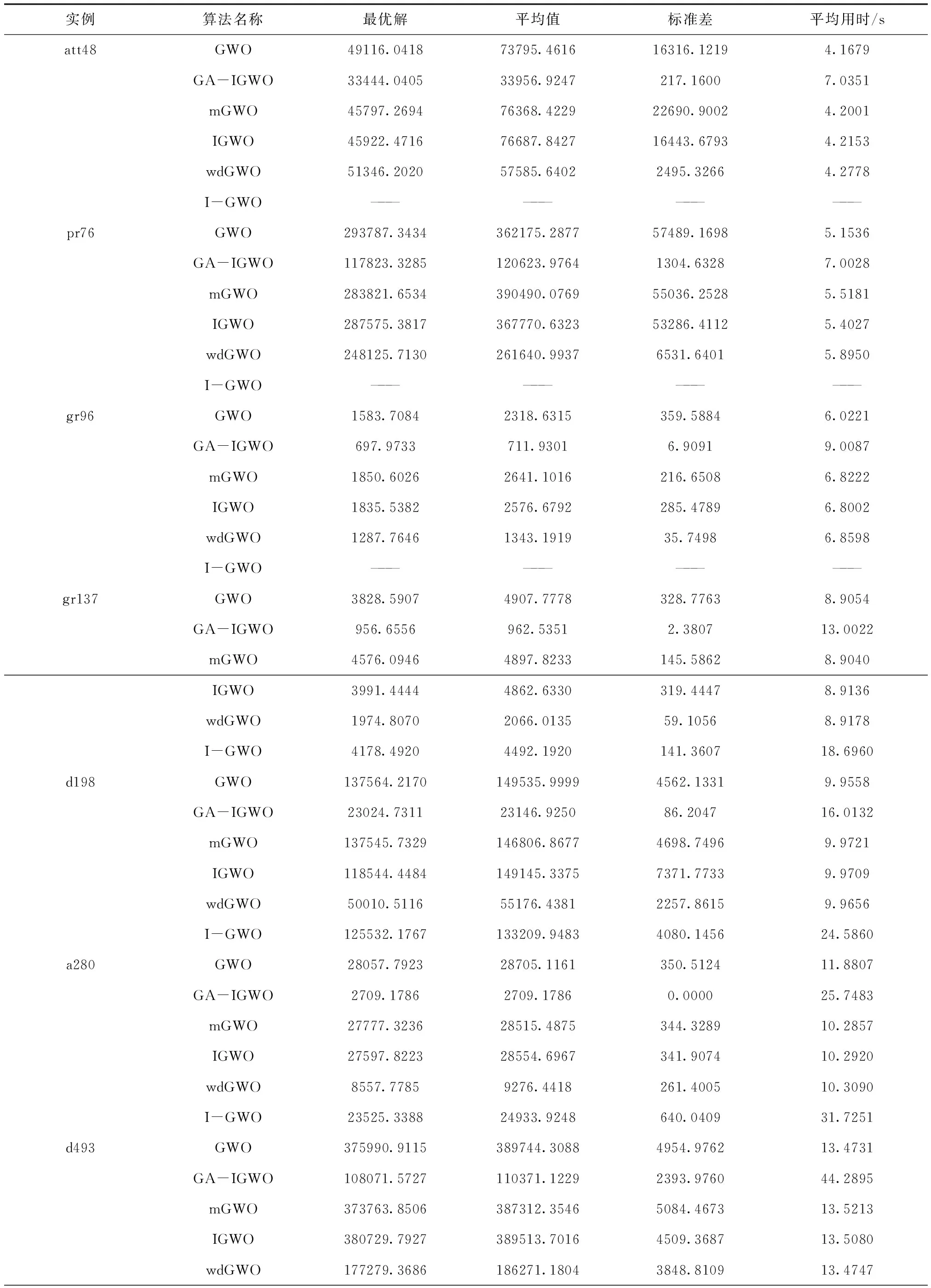
表1 GA-IGWO与其它改进GWO的实验数据

从表1的仿真结果分析,mGWO和IGWO是基于自适应函数a的取值方式进行改进,但与wdGWO和I-GWO基于搜索策略的改进方式相比较,显然基于搜索策略的改进方式更有利于求解TSP问题,而本文提出GA-IGWO算法与列举出来的四种改进的灰狼优化算法对比,在精度和稳定性方面都优于其它改进算法。

为进一步说明本文GA-IGWO算法的先进性,将其与目前在TSP问题中应用较广泛的遗传算法(GA)、模拟退火算法(SA)、禁忌搜索算法(TS)进行仿真对比。为确保算法能收敛至合适的可行解,各算法设置参数不同。其中GA和TS设置初始种群均为100,最大迭代次数均为1600;SA初始温度为目标节点数的100倍,马尔科夫链长度100,温度衰减参数0.99。仿真结果见表2。

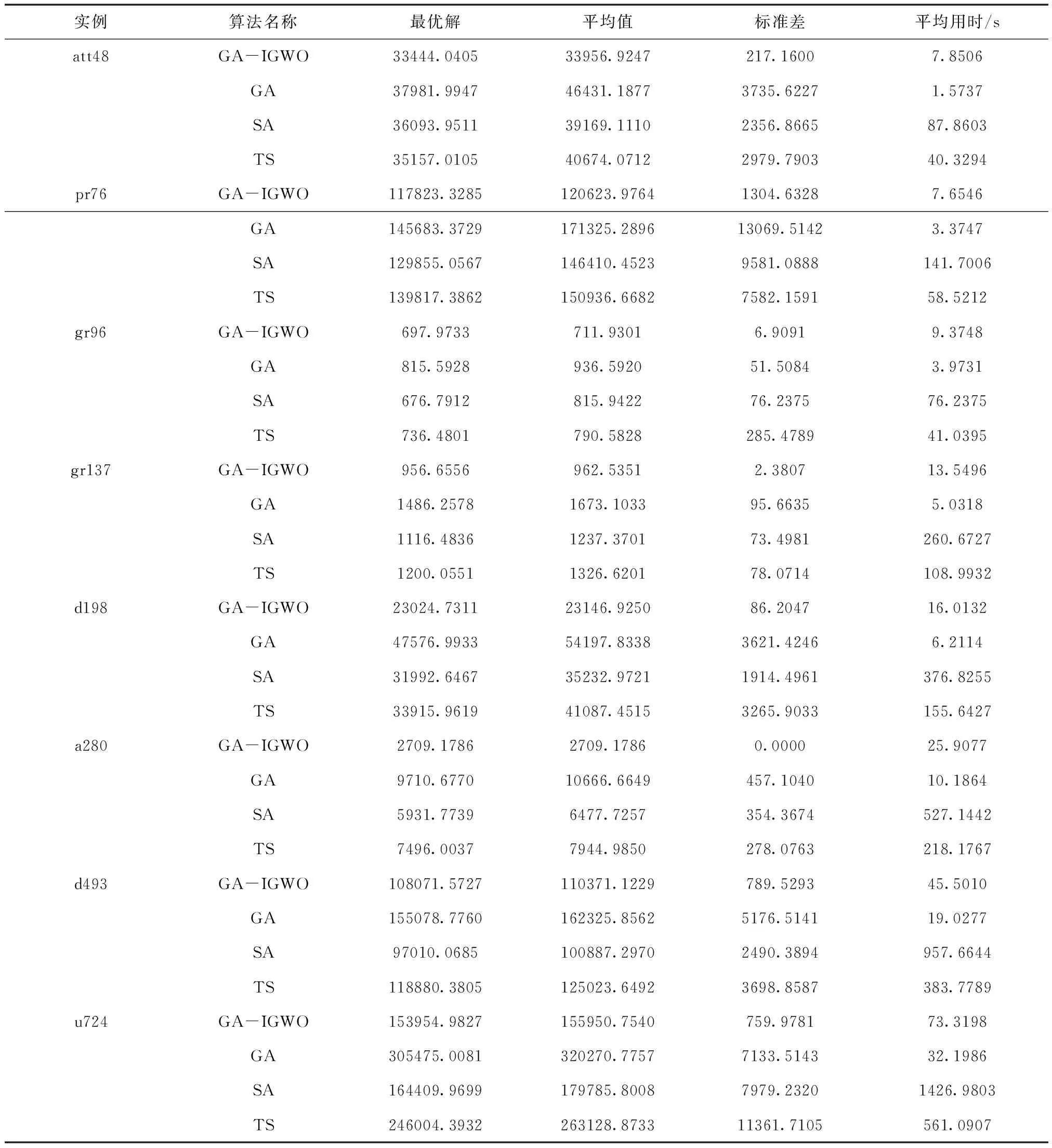
表2 GA-IGWO与其它智能算法的实验数据

从表2的仿真结果分析,在求解TSP问题时,相较于SA、TS和GA,GA-IGWO除了在求解时间上稍慢于GA,但在求解精度、稳定性方面均占一定优势。从以上分析中可以得知,本文提出的算法在求解TSP问题中表现良好,在收敛精度和稳定性方面均具有一定优越性。

5 结束语

本文从种群初始化和搜索策略两个角度对灰狼优化算法进行了改进,在利用遗传算法进行初始化种群筛选的同时将距离启发因子引入到灰狼优化算法的搜索策略中,提出了GA-IGWO算法,避免了GWO算法在求解TSP问题时,由于前三个可行解之间的差距过大而导致整个种群产生巨大误差的问题,同时提高了GWO算法的求解精度、收敛速度以及稳定性。

仿真结果表明,改进融合遗传灰狼优化算法在求解TSP问题时,保留了遗传算法的全局搜索能力和灰狼算法的局部搜索能力,并能利用较少的求解空间和时间得出最优解。但是仍然存在易陷入局部最优问题,所以下一步将在此基础上对如何提高灰狼优化算法在求解TSP问题时的精度进行进一步研究。