基于多约束算法的建筑空间利用率优化仿真

肖晓芳,朱国华,刘丽雅

(1. 重庆人文科技学院,重庆 401524;2. 江汉大学人工智能学院,湖北 武汉 430056)

1 引言

土地作为我国主要的地理资源,同时也是我国社会发展进程中主要依赖的因素,也是我国生态环境建设的主要载体。近年来对着我国城市化建设的逐步加快,在经济社会不断发展的同时,随着城市化进程过程中城市人口的不断增加与城市有限的土地资源之间的矛盾也变化日趋白热化。土地资源的限制下,不断加快的城市化进程越来越使得城乡居民的生活空间满意度越来越低。因此,在社会发展的进程中土地资源的短缺已经对我国城市化的社会、经济发展造成了极大的地域约束。因此,在推进城市化进程以及对应的城乡发展规划过程中,如何在有限的建筑空间内,提高建筑空间资源的录用率进行优化,从而实现我国国土资源的有效利用实现可持续发展、贯彻科学发展观,以及建立美丽乡村实现乡村振兴具有重要意义。

近年来随着现代建筑设计的快速兴起,越来越多的学者在建筑设计、空间利用率等方向做出了积极的研究和贡献。其中比较典型的研究如下,文献[11]从用地企业的角度,提出了基于用地企业方向的建筑空间利用率的优化算法,该方法的主要思想依旧采用传统的建筑空间优化方法,即随机抽样调差法;该方法在调研区域内抽取一定的企业建筑空间数据,然后该方法依照C-D生产函数理论模型,从而建立基于企业视角的空间找资源规划利用率模型。然后对建立的利用率模型进行计算,从而来进行优化计算。但是该方法存在的缺点在于,完全站在企业的视角来进行空间利用率计算,达不到区域或者整体优化的目的。文献[2]通过将城乡规划和城市化发展进程方面进行考虑,提出了一种基于极差思维的建筑空间利用率优化方法。该方法主要通过建立极差、离散系数、极差倍数等参数对我国城乡发展规划过程中的建筑资源利用率进行分析,从而进一步的反应我国在进行城市化进程中不同区域建筑空间利用率之间的差距。从而在资源配置、空间配置给出合理化指导建议。文献[3]针对现代建筑中比较典型的小户型建筑空间利用率优化问题,提出了基于粒子群的建筑空间利用率优化算法。该方法通过对待优化的空间进行分割,将分隔空间分别用平均建筑面积以及该面积大致的使用时间进行赋值粒子点,然后结合粒子点位置完成对设计方案的评估和优化。文献[4]提出采用这智能计算优化方法是未来建筑设计现代化发展的主要方向,在众多智能化优化设计方法中比较典型的有遗传算法、差分进化算法、蚁群算法、蜂群算法以及混合算法等。在众多的智能化优化算法中,其核心思想主要是和根据设计的输入约束条件,建立对应且符合实际的目标函数,并进一步的对目标函数求解。文献[5]针对西安高新技术产业区开发中遇到的问题,建立了基于空间资源调控的城市规划设计方法,然后在此基础上为西安高新区的发展指明了“城市巅峰、时尚高地”的城市规划形象,进一步的为城市规划提出了新的思路。文献[6]通过构建城市发展规划土地资源利用过程中的测度模型,对城市发展过程中的用地趋势和资源利用率进行对比分析,同时以浙江省土地资源配置为例,建立了基于比较优势的土地资源优化配置方法。文献[7]针对大型城市群中建筑空间的合理性设计与优化问题,结合城市建设过程中涉及的光照强度、环境温湿度等因素,采用多参量自回归的设计思路给出了对应的大型城市建筑空间优化设计模型。同时通过仿真验证了利用该方法建立模型的有效性和实用性。但是可以明显的看出采用该方法的局限性在于它仅仅以大型城市群建设为出发点,对于中小城市的建筑设计规划所遇到的问题相对较少。文献[8]着重研究了在城市化进程中,社会转型时期土地资源利用的空间重构进行了研究。提出建立空间重构效应的模型分析框架,同时从不同层次和不同方向进行了分析和研究,从而为我国加快城市化进程、优化土地资源空间配置提供了重要的科学理论依据。文献[9]根据近年来世界范围内城市在进行产业转型和产业重构特点,对近年来国内外城市转型发展进行了透视、分析了产业之间的内在关联,规划了产业变化、城市空间以及城市转型发展之间的内在关系,进一步说明了建筑空间与城市产业层次、城市产业内核等多种要素之间的相互影响。文献[10]根据党中央在我国经济会议的核心思想,进一步阐述了优化产业空间、提升城乡社会实体经济发展质量的重要论述。明确了以土地资源为核心、实现空间资源优化为目的、促进城市发展空间的转型升级的册罗和建议。文献[11]针对近年来我国城市发展过程中,新兴产业的涌现、变迁和发展对城市化发展进程中的经济活动、社会产业结构等的冲击,研究了新旧兴产业空间结构、城市空间结构规划之间的博弈关系。

综上可以看出,在城市发展转型、城市经济结构更新过程中,合理的资源规划对我国经济发展具有重要意义。本文针对多约束条件下,如何进一步优化建筑空间利用率,提出了基于最优理论的优化方法。该方法首先对待优化建筑空间进行建模;然后考虑空间约束、舒适度、建筑空间使用效益等方面进行数学意义提取和建模,同时构建以建筑空间利用最大化为目标的目标函数。最后采用动态划归最有理论文成对目标函数的求解。文章最后给出了不同条件下的数字仿真,进一步验证了本文提出方法的有效性。

2 建筑空间优化建模

2.1 动态规划理论

动态规划(Dynamic Programming)算法作为运筹学的一个主要分支、同时作为求解最优问题的主要主要方法,其算法核心思想是:将待求解的最优化问题进行逐步的划分,将原始问题逐步分解成以一个具有链接关系的小问题进行解决,寻求每个小问题对应的最优解,从而将整个过程进行统一分析,进而得到整个过程的最优解。如图1所示,为典型的动态规划理论求解最优控制原理示意图。

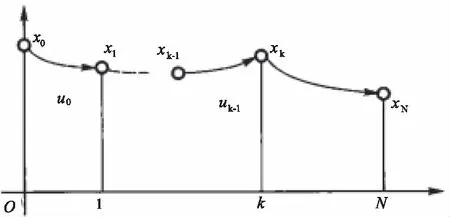
图1 最优性原理示意图

图2 多级决策过程示意图

首先建立描述一个该系统的离散系统的状态方程

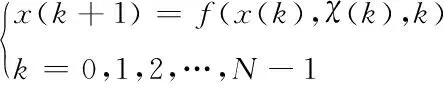
(1)

其中,χ(k)表示不同节点下的空间优化决策。控制决策满足如下条件

χ(k)=X

(2)

最终的优化性能指标为

(3)

最优指标为

V(x0,k0)=∑min(X)J(χ,x0,k0)

(4)

最优决策的重要条件为

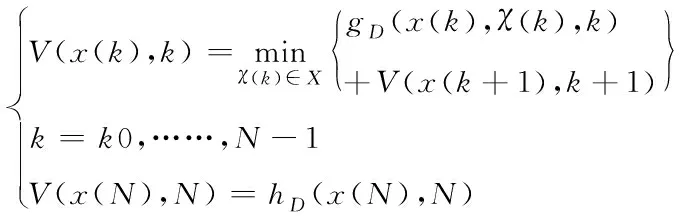
(5)

根据最优化条件,直接对系统从最后时刻、最后的一个节点进行迭代求解,进而得到整个系统的最优解。

2.1.1 优化约束建模与分析

在解决多约束条件下建筑空间利用率的优化过程时,本节论文主要分析优化过程面临的约束因素,同时根据约束条件与空间利用率之间的关系,建立对应的数学约束模型。

a) 空间整体约束Cv

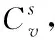
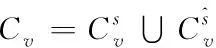
(6)

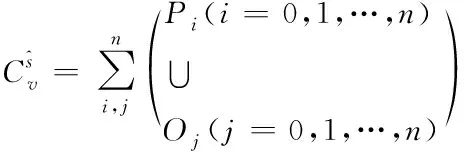
(7)

b) 位置约束Cp

位置约束主要描述在进行空间规划过程中,对目标进行规划时必须考虑与其它特定目标之间的相互影响,从而使得待规划目标必须满足对应的空间位置约束。

(8)

c) 建筑空间颗粒度约束Cb

建筑空间颗粒度约束主要表示为在进行建筑空间网格化标定的过程中,如何选择较为合适的颗粒度以满足对布局目标类型的全覆盖。因此,在进行对建筑空间进行颗粒化的过程中定义颗粒度约束为

(9)

2.1.2 优化约束建模

在构建数学约束之后,采用动态规划的思想构建整个约束过程中建筑空间优化离散系统状态方程如下

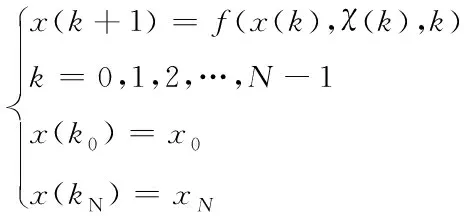
(10)

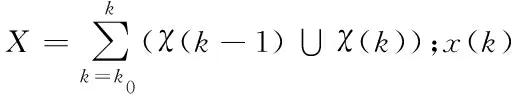
在构建建筑空间优化系统的约束条件时,首先以当前比较典型的办公空间为里进行构建

(11)

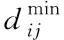
第k个目标规划的规划决策满足如下

χ(k)∈X

(12)

在构建完成系统状态方程和目标约束后,构建系统性能指标函数如下

(13)

在进行求解最有规划决策χ的过程中,首先定义起点为k时

(14)

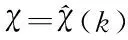
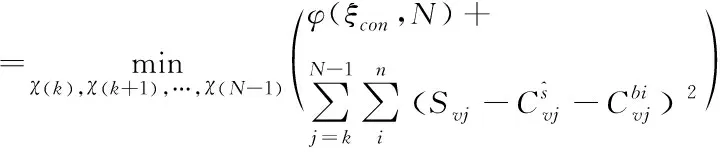
I(x(k+1),k+1)

(15)

其中,式(15)为对应的最优情况下的建筑空间最优化贝尔曼方程。

2.1.3 递推求解

在对多级优化问题进行求解的过程中,采用逐级递推方发来完成对应最优多级优化问题,其中求解步骤如下:

Step1:

当k=N-1时,性能指标如下

(16)

其中,hd,L等于式(15)中内容。依次地推迭代进行;

step2:

当k=N-2时,求解在χ(N-2)时的最小化问题:

(17)

按照反向一次地推计算。

Step N:

当k=0时,

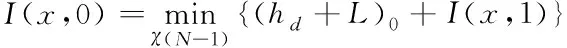
(18)

3 数字仿真与验证

为了进一步验证本文提出方法的有效性,文章分别采用了基于粒子群优化方法建筑空间利用率优化的方法进行对比,仿真参数见表1。

表1 仿真参数

分别采用和不用方法的仿真结果如图3-4所示。

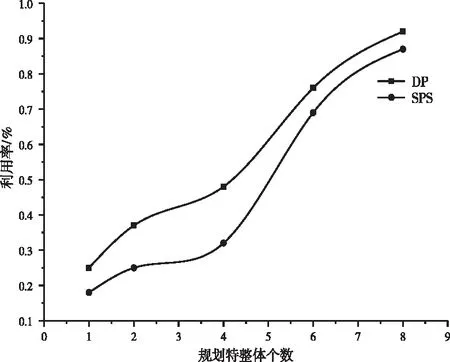
图3 DP-SPS空间利用率对比

如图3所示,分别表示采用本文提出的动态规划方法(DP)和粒子群方法(SPS)对建筑空间利用率进行优化的结果。通过曲线可以看出采用本文提出的优化方法可以使得空间利用率得到很大的提升。

为了进一步验证算法的有效性,同时验证不同方法对不同的特征体进行空间布局时的空间利用率,对同样数量不同类型的特征体进行优化的结果如图4所示。

图4 不同特征体对应的空间利用率对比

如图4所示,在相同数量特征体的情况下,采用本文提出的方法在空间利用率上明显优于粒子群优化方法。

4 结论

本文针对传统优化无法完整满足建筑空间特征优化的问题,提出了基于动态规划的建筑空间利用率优化算法。首先,针对建筑内的空间特征进行建模和分析,同时将不同约束条件进行数学描述;其次,对影响空间利用率的因素进行归纳分析,依次建立影响空间利用率条件的约束函数,同时建立建筑空间利用率最大化的目标函数;最后,根据动态规划理论目标函数进行求解。最后文章从不同角度进行数字仿真,通过仿真可以看出,采用本文提出的方法在空间利用率方面具有很好的效果。