Chebyshev-Padé型极点降阶及传输线方程应用
刘 萌,苗 真,蒋耀林,
(1. 新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046;2. 西安交通大学数学与统计学院,陕西 西安 710049)
1 引言
随着现代集成电路技术的快速发展,各类器件大规模集成化以及信号频率不断提高,大型或复杂动力系统仿真给工程技术人员带来了巨大的挑战。为了解决这个问题,必须给出新型的仿真方法来降低系统的复杂程度和分析难度,进而减少计算量,提高计算效率。这一背景下模型降阶方法应运而生,其主要思想是用一个小规模的系统去近似原始大规模系统,降阶系统在允许误差范围内保持系统输入输出特性的同时还要保持原始系统的稳定性、无源性等主要性质[1,2]。
在模型降阶方法成体系出现之前,Padé逼近作为一种近似传递函数的方法,在数学领域已经被广泛应用。以Padé有理逼近思想为基础,进一步产生了渐近波形估计方法(AWE),它是一种显式矩匹配方法[3],通过包含相对少量的主极点和零点的降阶模型来近似传递函数。虽然电路可以产生大量的极点和留数,但在特定的频率范围内,所有的极点和留数的贡献并不一定相等。瞬态响应通常可以由较少的主极点和留数控制,AWE方法可以提取这些主极点和留数,从而构建低阶的传递函数,在合理精度内逼近电路的原始响应。这种方法只适用于较小规模的系统,其主要考虑降阶系统如何保持系统的矩。文献[4]提出了面向脉冲响应矩的计算方法,对大规模系统进行矩匹配过程提供了理论基础。矩匹配类方法的基本思想是使降阶后的传递函数匹配原始系统传递函数的前若干矩。针对单输入单输出系统,文献[5]利用矩的概念研究了线性和非线性系统的模型降阶问题。文献[6]提出了一种获得线性系统传递函数最优降阶模型的新方法。它以迭代的方式使用多点Padé逼近来高效地生成最优模型。该方法通过将多个点的Padé逼近简化为等价的Taylor级数来计算近似值。一维AWE的研究逐渐成熟,文献[7]提出了M-D AWE方法,该方法将一维的AWE方法推广至任意m维。一阶极点AWE方法无法处理重复极点问题,文献[8]将传统的一阶极点方法推广到高阶极点情形,提出了广义AWE模型降阶方法,对AWE方法进行了扩充。将有理逼近相关理论应用到模型降阶领域当中,有助于提高模拟精度,例如,与经典Padé逼近相对照,Chebyshev-Padé逼近具有良好的整体逼近性质,且非常接近最佳一致有理逼近[9]。
本文在传统AWE算法的基础上提出Chebyshev-Padé型极点降阶算法,使之能够处理含重复极点的复杂问题,并进一步将其应用至传输线方程中。所提出的基本方法能够在很少的降阶阶数下提高模型的近似精度。
2 Chebyshev-Padé型极点降阶算法
本节主要介绍Chebyshev-Padé型极点降阶算法,分别讨论单重极点和多重极点情形。
考虑线性时不变系统
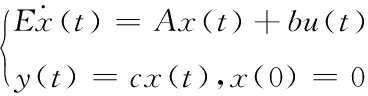
(1)
其中E,A∈Rn×n是常数矩阵,b∈Rn×1,c∈R1×n,x(t)∈Rn是系统的状态变量,u(t)∈R是系统的输入变量,y(t)∈R是系统的输出变量。系统(1)经Laplace变换后满足Y(s)=H(s)U(s)=c(sI-A)-1bU(s),其中Y(s)是y(t)的Laplace变换,U(s)是u(t) 的Laplace变换,H(s)表示系统的输入输出关系,即为传递函数。可简记系统(1)为{E,A,b,c}。
2.1 Chebyshev多项式及其性质
定义1[9]多项式
Tn(x)=cos(narccosx),-1≤x≤1,n=0,1,…
称为Chebyshev多项式。
性质1[9]Tn(x)=2xTn-1(x)-Tn-2(x),n=2,3,…
T0(x)=1,T1(x)=x
性质2[9]Tn是首项系数为2n-1的n次代数多项式,且T2k(x) 只含x的偶次幂,T2k-1(x)只含x的偶次幂。
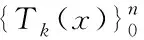
GT(x)=X
(2)
其中
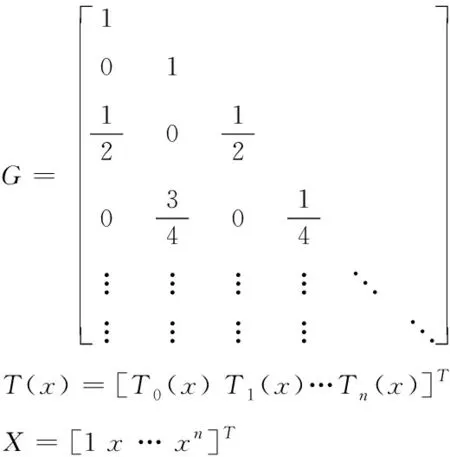
(3)
2.2 Chebyshev-Padé型极点降阶
对于线性时不变系统(1),将传递函数H(s)在s=0处做Taylor级数展开,可得
(4)
将传递函数H(s)在s=∞处进行Laurent展开,可得
(5)
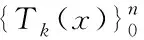
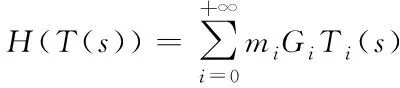
(6)
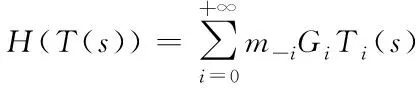
(7)
记Ci=miGi,C-i=m-iG(i=1,2,…)为广义矩,其中Gi表示G的第i行。
用下述函数对原始系统进行有理逼近
(T(s))

(8)
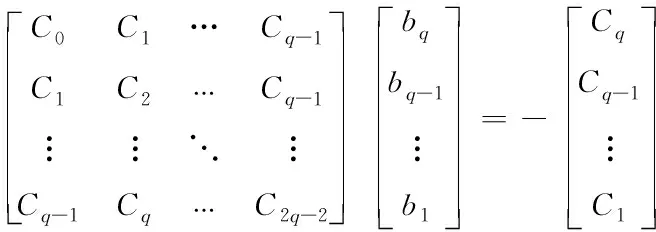
(9)
(T(s))=1+b1T1(s)+…+bqTq(s)
(10)

(11)
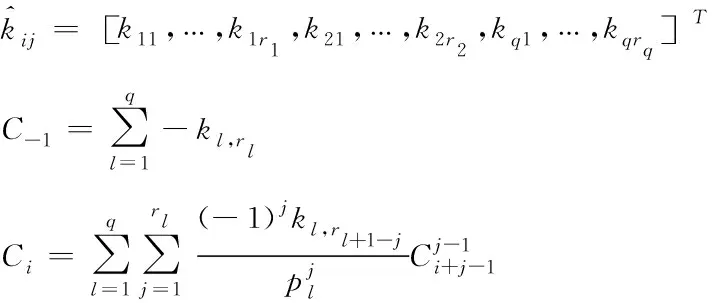
(12)
上述降阶过程可用算法1来描述。
算法1:Chebyshev-Padé型极点降阶算法
输入:线性系统{E,A,b,c},降阶次数q
2) 将H(s)转化为Chebyshev多项式
2.3 Chebyshev-Padé型逼近定理
为便于描述,下面简记矩阵
(13)
(14)
存在的充分必要条件是
rank{HC(L,M-1,M-1)}=rank{HC(L+1,M,M-1)}
(15)
证明:由于
(16)
成立的充分必要条件是方程
QM(T(s))H(T(s))-PL(T(s))=O(s(L+M+1))
(17)
有解,令(17)式两边对应系数相等可得
(18)
进一步,方程(18)可改写为
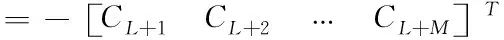
(19)
方程(18)和(19)的系数矩阵分别为HC(L+1,M,M-1)和HC(L,M-1,M-1),因此(17)式有解的充要条件为方程组系数矩阵和增广矩阵具有相同的秩,即定理结论成立。
推论1 若矩阵HC(L,M-1,M-1)是非奇异的,则函数H(T(s))存在有理逼近式
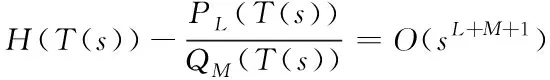
(20)

3 传输线系统的降阶
本节将上述算法应用于传输线系统。传输线是一种导行电磁波结构,多导体传输线(MTL)的应用涵盖了很宽的频域范围和各种传输线类型,从工频输电线路到微波电路。对于n+1个平行于z轴的导体构成的MTL,其传输线方程是一组耦合的2n个关于n个电压Vi(z,t)和电流Ii(z,t) (i=1,2,…,n)的一阶偏微分矩阵方程。大量的导体会产生巨大数目的耦合MTL系统,为了方便计算,需要降低结构的表征阶数,用较少的有限个主导极点表示MTL传输函数[10]。
3.1 传输线模型
假设导体为理想导体,包围在导体周围的介质是均匀的,考虑传输线上的一个微分长度单元,可由单位长度电阻R,单位长度电感L,单位长度电导G,单位长度电容C对其进行描述。对传输线做出以下两个假设:1)传输线的横向尺寸在其长度方向上是连续的;2)传输线上的电磁波为准TEM波,即传输线上沿波传输方向的电磁分量远远小于其横向分量。设i(x,t)与v(x,t)分别为传输线上x处的分布电流和分布电压,根据基尔霍夫电压定律KVL和基尔霍夫电流定律KCL可得如下传输线系统方程

(21)
其中R为电阻,L为电感,G为电导,C为电容。关于时间t做Laplace变换,可得
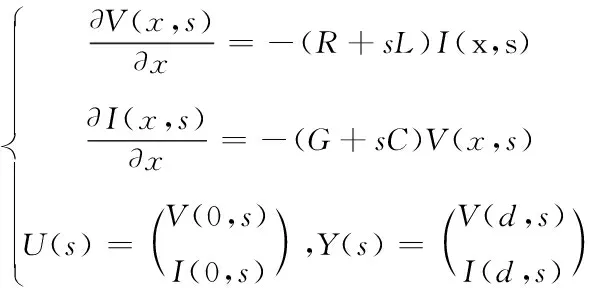
(22)
其中V(x,s),I(x,s),U(s),Y(s)分别表示,v(x,t),u(t),y(t)经过Laplace变换后的函数。可以将系统写为如下矩阵形式

(23)

对传输线方程使用有限差分进行空间离散,将其转化为状态方程形式
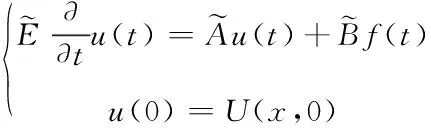
(24)
其中
3.2 传输线模型的降阶方法
对H(s)在s=0处做Taylor级数展开得
(25)
即Mi为系统的矩。对H(s)在s=∞处做Laurent级数展开得
(26)
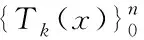
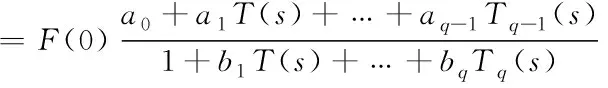
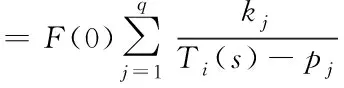
(27)
其中F(0)=F(s)|s=0是直流响应,且
(T(s))=a0+a1T(s)+…+aq-1Tq-1(s)
(T(s))=1+b1T(s)+…+bqTq(s)
通过比较F(T(s))(T(s))=F(0)(T(s)) 中的项Ti(s)(i=q,q+1,…,2q-1)的系数,可得到如下线性方程组
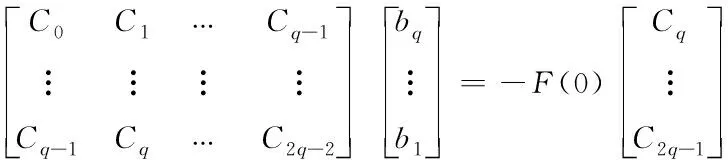
(28)
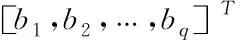
若pi≠pj(i≠j),将pj代入下式,得到关于kj(j=1,2,…,q)的线性方程组
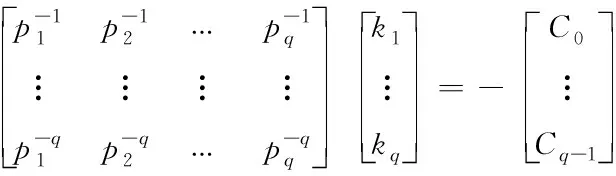
(29)
否则通过如下线性方程组求解出留数
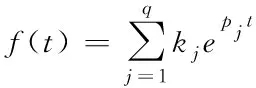
4 数值实验
为验证本文算法的有效性,下面给出两个数值算例。
例1 考虑如下的线性时不变系统

(30)
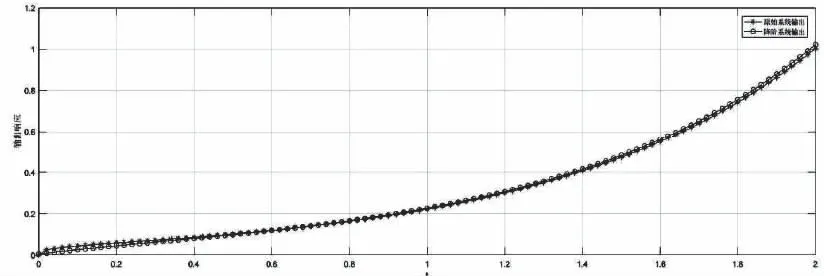
图2 n=300,q=2时的系统输出响应对比
由输出响应对比图可以看出n=300时,q=2的降阶系统的输出响应与原始系统的输出响应曲线拟合程度更好。为了进一步表示算法的降阶效果,在图3、图4中分别给出了基于Chebyshev-Padé型极点降阶算法与传统AWE的原始系统与降阶系统的输出相对误差对比。

图3 n=300,q=3时的系统输出相对误差
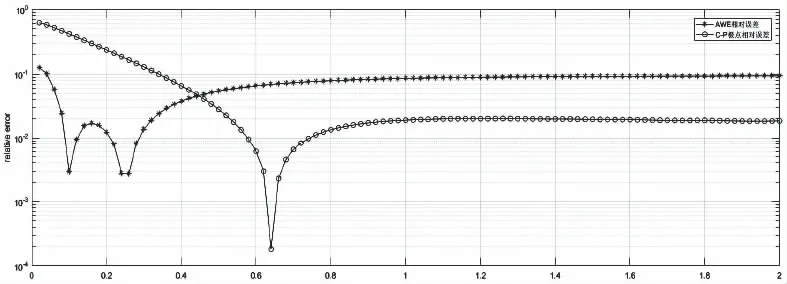
图4 n=300,q=2时的系统输出相对误差
由相对误差响应图可以看出系统在较长时间模拟时,两种算法均在q=2时的相对误差更小。相比之下,Chebyshev-Padé型极点降阶算法的相对误差比传统AWE更小。
例2 考虑一根半径为rw=10mils,长l=1 m的导线位于无限大接地平面以上,距地高度h=2 cm。导线的电阻为5Ω,电感为L=3*10-4μH,电容为C=2.5*10-3μF。通过空间离散可得600阶的传输线系统。分别采用Chebyshev-Padé型极点降阶算法与传统AWE,将上述传输线系统降至2阶,得到如下结果。
图5和图6分别显示了该传输线系统的传递函数在频域上的幅值和相对误差,可以看出将600阶的传输线系统降至2阶时,Chebyshev-Padé型极点降阶算法的传递函数频域幅值拟合效果良好,且拟合度相较AWE更高,具有明显优势。
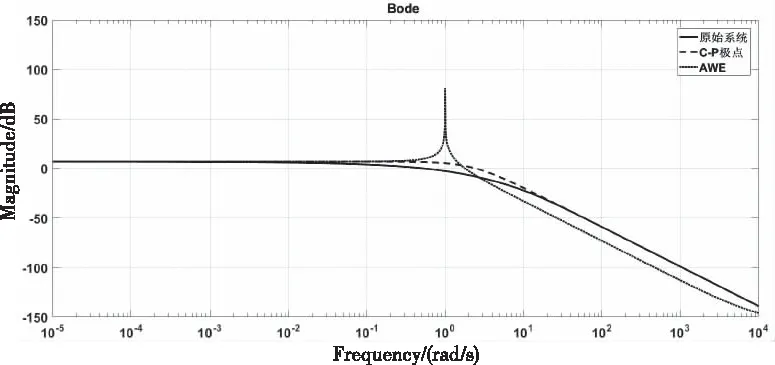
图5 n=600,q=2时的传递函数幅值对比
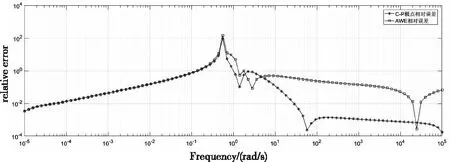
图6 n=600,q=2时的传递函数幅值相对误差
5 结论
本文提出了Chebyshev-Padé型极点降阶算法,通过将传递函数展开为Chebyshev级数,可以在匹配较少的广义矩的条件下得到更为精确的降阶系统。此外,根据传递函数的极点重数的不同情形可以通过Chebyshev-Padé型极点降阶算法得到对应的留数,并进一步获得传递函数和输出响应。将该算法应用于传输线模型中,其数值结果表明降阶系统能够较好地近似原始系统。

