中子测量用慢化体及热中子转换层厚度优化

黄广伟,吴 坤,周春芝*,张逸韵

(1. 国民核生化灾害防护国家重点实验室,北京 102205;2. 中国科学院半导体研究所照明研发中心,北京 100083;3. 中国科学院大学材料科学与光电技术学院,北京 100190)

1 引言

因中子不带电,对其探测必须采用核反应法、核反冲法、核裂变法和核激活法来产生次级带电粒子的间接测量方法。核反应法常用的中子灵敏材料有10B、6Li和3He等[1-3],它们具有热中子反应截面大、反应能较高的特点,但当前3He气体日益短缺,使其应用变得成本高昂。与之相比,将富集10B、6Li的稳定化合物(如B4C、LiF)通过一定技术手段转移到电离辐射探测器表面,然后通过测量带电粒子产物的方式来测量中子是制备中子探测器常用的方法:唐彬等利用SiC和LiF制备了中子探测器,且可以通过简单设置阈值有效分辨γ射线[4];Makoto I. Kobayashi等使用基于CVD金刚石和LiF的热中子探测器测量了252Cf中子场和D-D聚变中子场,同时提出了针对该探测器的n/γ脉冲波形甄别技术[5];包括目前广泛研究的涂硼稻草管探测器[6]、涂硼多气隙电阻板室[7]等,均是基于这种思路设计的中子探测器。基于转换层的中子探测器的探测效率有两个关键影响因素:一是由于10B、6Li的中子截面随中子能量提高而下降,为提高热中子通量,通常需要在探测器前增加适当厚度的慢化体[8];二是由于中子转换材料对次级带电粒子产物,尤其是重带电粒子的自吸收问题,导致其探测效率受转换层厚度影响很大[9]。从实验上同时优化这两个参数的成本和难度较大,本文以常见的252Cf中子源、聚乙烯(C2H4)慢化体和B4C/LiF中子转换材料为例,建立蒙特卡洛粒子输运模型,得到了针对该模型下的最优慢化体和中子转换层厚度,并通过理论推导和计算验证了模型的准确性。

2 算例描述

图1为本文计算的场景示意图,由252Cf中子源、聚乙烯慢化体、B4C/LiF热中子转换材料和探测器组成,252Cf中子经过慢化体后中子能量降低,与10B的相互作用截面变大。热中子与10B的相互作用方式如下[10]

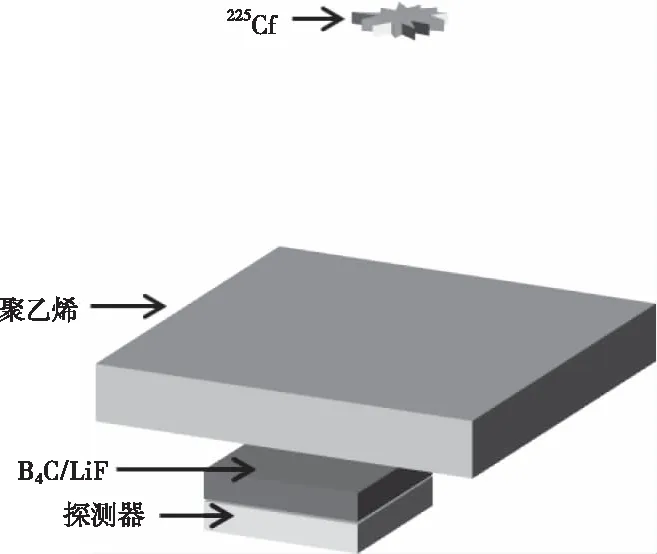
图1 算例描述的场景示意图

10B+n→7Li+α+2.792MeV 6.1% 反应道1

↘7Li*+α+2.31MeV 93.9% 反应道2

↘7Li+γ+0.478MeV

(1)

该反应有两个反应道,忽略反应初始动量,根据能动量守恒易得出其带电粒子产物α/7Li粒子的能量在反应道1和反应道2中分别为1.78MeV/1.02MeV和1.47MeV/0.84MeV。在这些粒子的能量可以完全沉积的情况下,它们的射程在B4C和探测器中基本是确定的,探测器通过测量α/7Li产物实现对中子的间接探测。热中子与6Li的相互作用方式与之类似,产物分别为2.735 MeV的3H和2.051 MeV的α粒子。

3 蒙特卡洛模拟

本文的中子输运过程模拟所用的程序是Geant4(10.5版本)[11],物理模型为QGSP＿BERT＿HP,可高精度地计算中子输运过程,相互作用截面库选用CENDL-3.1;α和7Li粒子在B4C中的射程利用SRIM-2013.00的TRIM程序计算得出[12];后续粒子出射判断和相关统计利用Matlab R2016b编程实现。

3.1 计算方法

需要指出的是,虽然实际测量场景下信号是被探测器记录的,并且可以在建模过程中设置不同转换层厚度,通过记录探测器中的能量沉积情况得到相关结果,但是由于仿真计算环境需要优化的参数较多,直接记录探测器的信号会显著增加计算成本,且不同探测器之间的差异也会使结果的适用性降低。因此本文提出了优化厚度计算的新方法:基于转换层中的粒子能量沉积情况,并结合粒子能否出射转换层的判断来进行相关厚度的优化计算。整体的计算思路为:利用Geant4计算252Cf中子穿过不同厚度的慢化体,并记录转换层中产生能量沉积事件(event)的各个步(step)粒子种类、反应的位置和粒子动量等信息,对于B4C,结合两个反应道的发生概率通过随机抽样获得α和7Li粒子的能量,对于LiF,3H和α粒子的能量为确定值。利用SRIM计算获得不同能量粒子在转换层中的射程,最后根据反应发生的位置和产物动量判断不同厚度转换层条件下出射的粒子数量。这里默认出射的粒子能量可完全沉积到后方探测器,对于半导体(如Si、SiC和金刚石等)探测器而言,因重带电粒子短射程的特点,这是容易做到的[13]。具体的流程如图2所示。

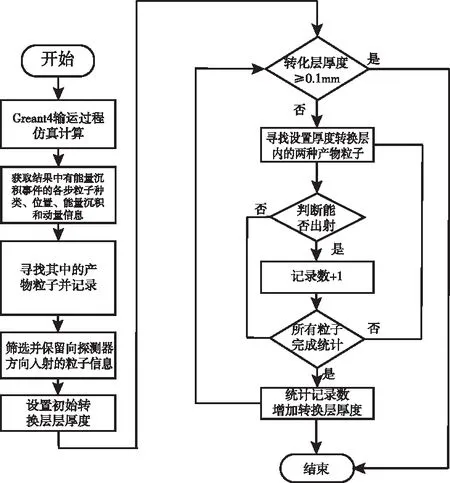
图2 仿真计算流程图

3.2 重带电粒子射程计算

利用SRIM-2013.00的TRIM程序计算中产物粒子入射对应转换层材料,以能量1.78 MeV的1000个α粒子垂直入射B4C的中心位置为例,设置B4C的密度为2.52 g/cm3,厚度为5 μm,得到的粒子径迹、能量损失和射程结果分别如图3(a)、(b)、(c)所示。

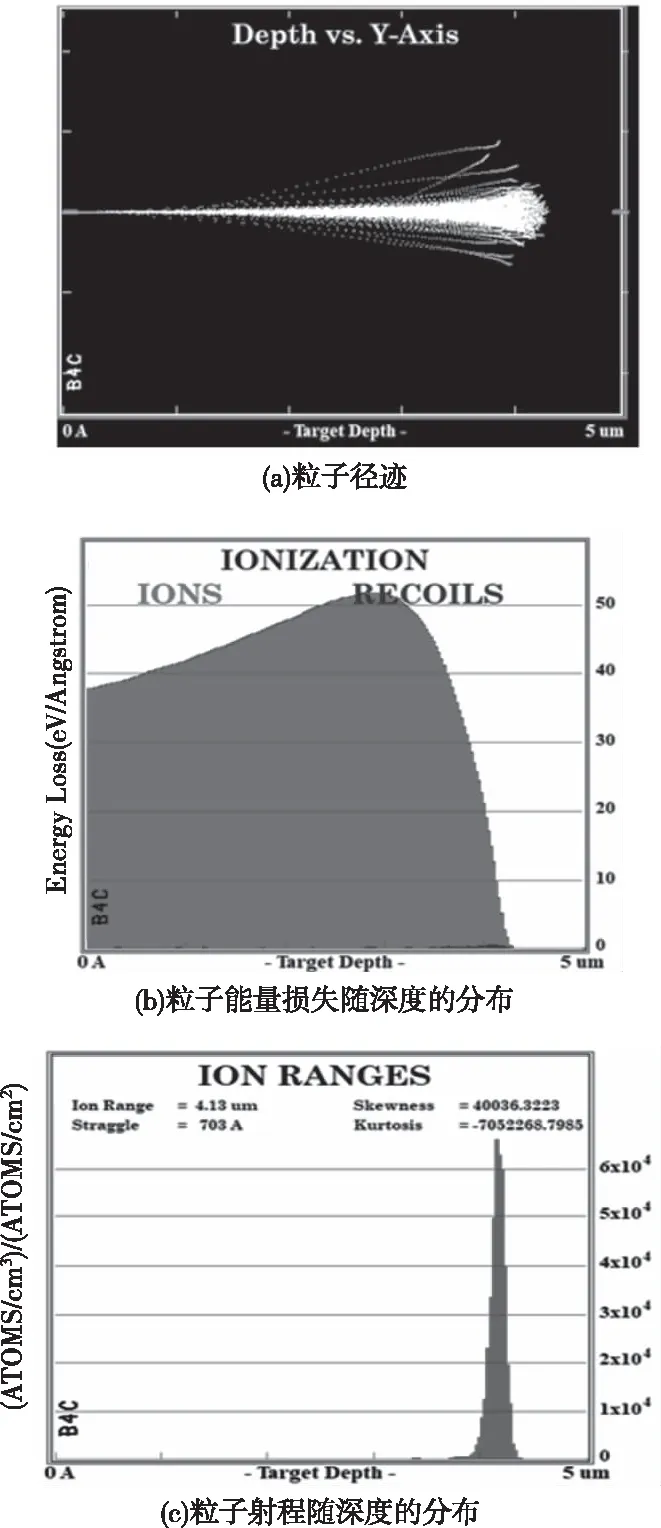
图3 SRIM计算结果

其它粒子的计算与上述过程类似,将计算结果汇总于表1。

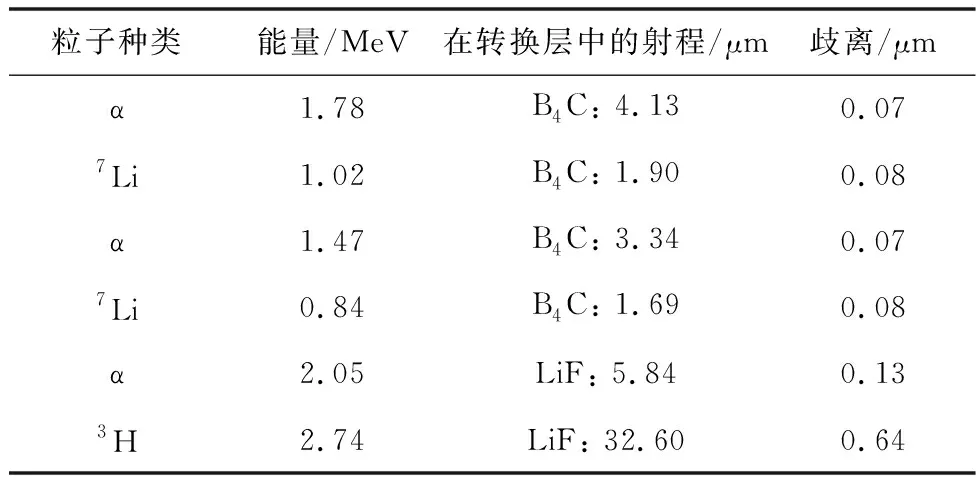
表1 反应产物在对应转换层材料中的射程

3.3 仿真参数设置

252Cf中子源设置为点源,4π方向发射中子,其出射中子能量根据标准中子谱抽样得到(图4);放射源距离慢化体距离为80 cm,中间介质为空气;慢化体材料为聚乙烯(C2H4),密度0.96 g/cm3,尺寸为16.6 cm×16.6 cm,厚度从0.5 cm到20 cm不等;中子转换材料分别为B4C和LiF,与聚乙烯等大,厚度为100 μm。

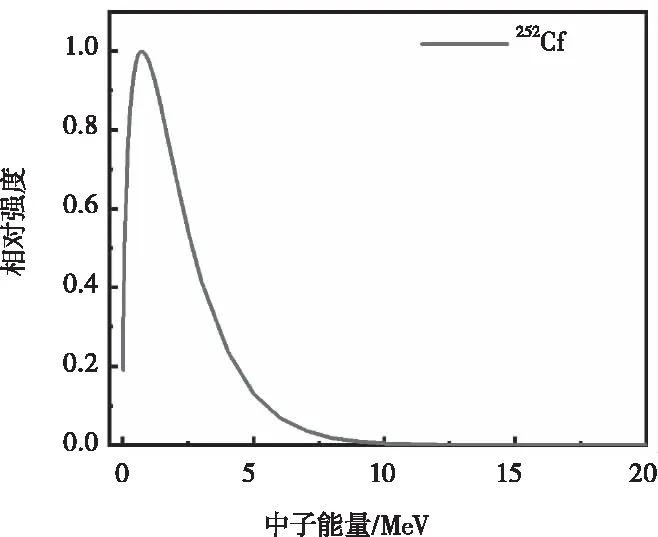
图4 252Cf中子发射能谱

3.4 计算结果与讨论

统计转换层中产生能量沉积事件的中子能量,可得到经历不同厚度慢化体后的可与转换层发生相互作用的中子能谱,如图5所示。

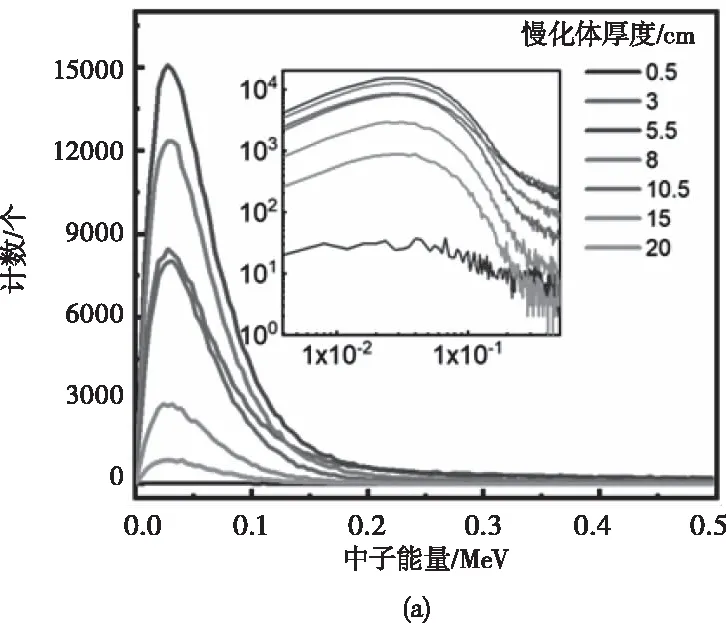
图5 252Cf中子经过不同厚度慢化体后与转换层相互作用的中子能谱 (a) B4C (b) LiF

从图5中可以看出,随慢化体厚度增加,其相互作用中子数量呈先增加后减少的趋势。进一步地,记录不同厚度慢化体下产物粒子数量,对于不同产物,可以发现二者数量基本一致,总是成对产生,证明确实有核反应发生。图6展示了B4C和LiF内发生的核反应数随慢化体厚度的变化关系,整体呈先增加后减少的趋势,均在慢化体厚度为5.5 cm时核反应数最多。

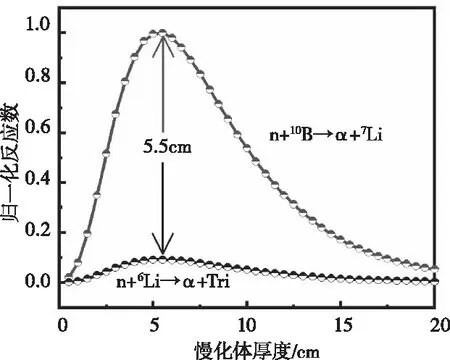
图6 B4C和LiF内核反应数随慢化体厚度的关系(依据B4C内最大反应数进行归一化)

在最优慢化体厚度下,结合产物粒子的动量及位置信息,计算并统计不同厚度转换层中可以出射中子转换层被探测器接收的粒子数(图7)。结果表明出射粒子数均随转换层厚度呈先上升后下降的趋势,B4C和LiF的厚度分别在2.8 μm～3.3 μm和33 μm～35 μm厚时出射粒子数最多,即此时探测效率达到最大。该趋势归因于反应产物在转换层中的自吸收:探测效率由核反应发生的数目和产物粒子能否出射转换层共同决定,核反应数目只与中子通量有关,能否进入灵敏体积则与带电粒子产生的位置及其动量相关。当转换层比较薄时,核反应发生数目随厚度增加,因此曲线前部分呈上升趋势;当转换层厚度继续增加,在远离探测器一端产生的粒子无法穿透转换层进入探测器,这部分对探测效率没有贡献,反而使靠近探测器一端中子通量变小,由于6Li的热中子截面小于10B,因此下降的趋势不明显。

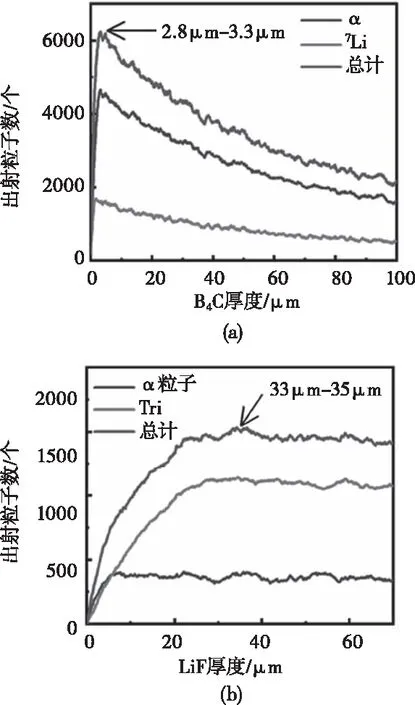
图7 出射转换层的核反应产物粒子数随转换层厚度的关系 (a) B4C (b) LiF

此外,在计算过程中统计B4C产物粒子动量时发现,沿中子入射方向出射转换层的产物粒子占比超过该粒子的一半(α:71.37%,7Li:52.33%)。这可能是由于热中子本身携带能量不可忽略导致的:热中子虽然能量很低,但对产物的动量仍有贡献,这种贡献对于较轻的α粒子动量的影响相比7Li更加显著,在大量粒子统计下这种现象被进一步放大。为证明该观点,统计了α粒子和7Li粒子的动量分布情况(图8),动量为1表示与中子入射方向相同,-1即相反。

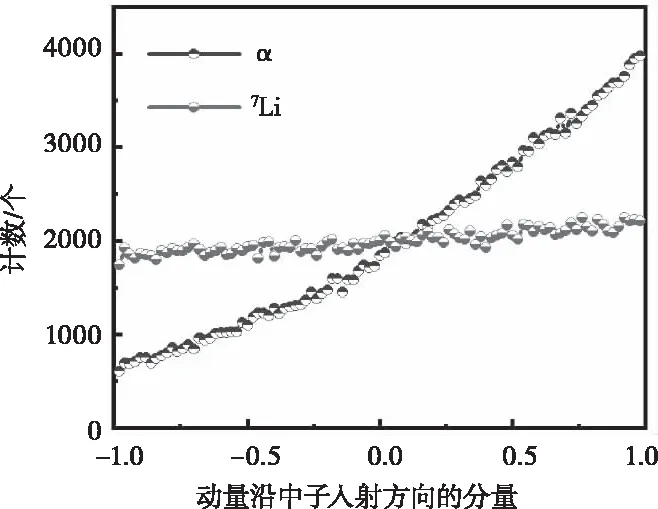
图8 反应产物粒子沿中子入射方向动量分布

从图8可以看出,反应产物动量分布在沿中子入射反向逐渐增加,该结论对于LiF转换层同样适用。这对于实际测量的指导意义是:对于单面转换层型热中子探测器,在测量中子时使转换层面朝向中子入射方向会提高探测器的探测效率,尤其是对于原子质量较小产物而言。

4 理论分析与计算

在理论分析最优中子转换层厚度的过程中,对输运模型进行了一定简化:假设入射粒子为单能热中子;对于B4C,发生的核反应仅保留反应道2;并忽略热中子能量对反应产物动量的影响。以B4C的α粒子产物计算为例,分析模型如图9所示。

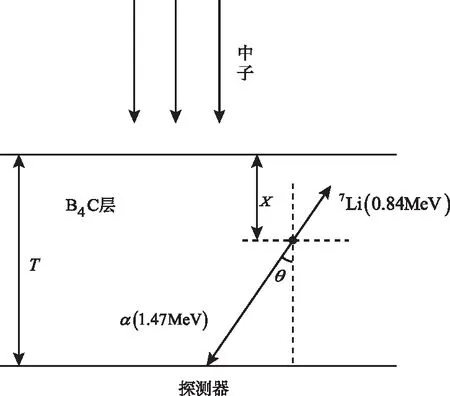
图9 理论分析模型示意图

假设深度x处中子束流强度为I(x),经过dx转换层后束流强度将减少,其变化量记做dI,束流经过dx厚度转换层后发生作用的热中子数是I(x)·Ndx,因此有

-dI=I(x)Nσsndx

(2)

式(2)中:N是转换层单位体积原子数,σsn为热中子俘获截面。

考虑到x=0时I=I0,解此微分方程,有

I(x)=I0e-σsnNx≈I0(1-σsnNx)

(3)

当α粒子在位置x产生时,定义可进入探测器的临界角θ为:

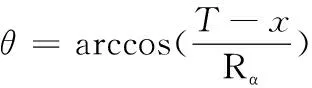
(4)

式(4)中:T为B4C的厚度,Rα为α粒子的射程(见表1)。则α粒子进入探测器的概率P即为顶角为2θ的圆锥立体角与4π的比值,即

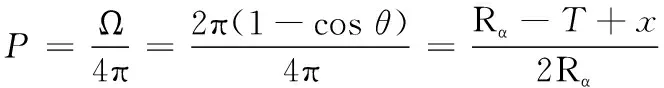
(5)

则在深度x处产生的α粒子进入探测器的束流为:

Idetector(x)=I0(1-σsnNx)·NσsndxP

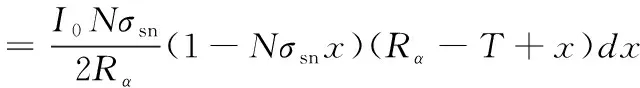
(6)

因此在整个转换层内进入探测器的α粒子束流为:

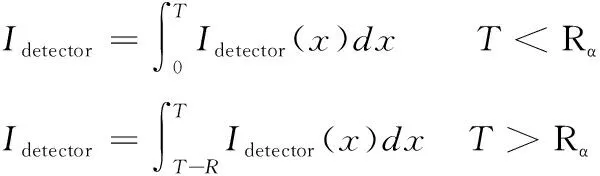
(7)

对于7Li粒子,有类似的推导过程,这里不再赘述。最终进入探测器的总粒子个数为两种粒子个数之和。

对式(7)的方程代入相应数值进行计算,结果如图10所示。

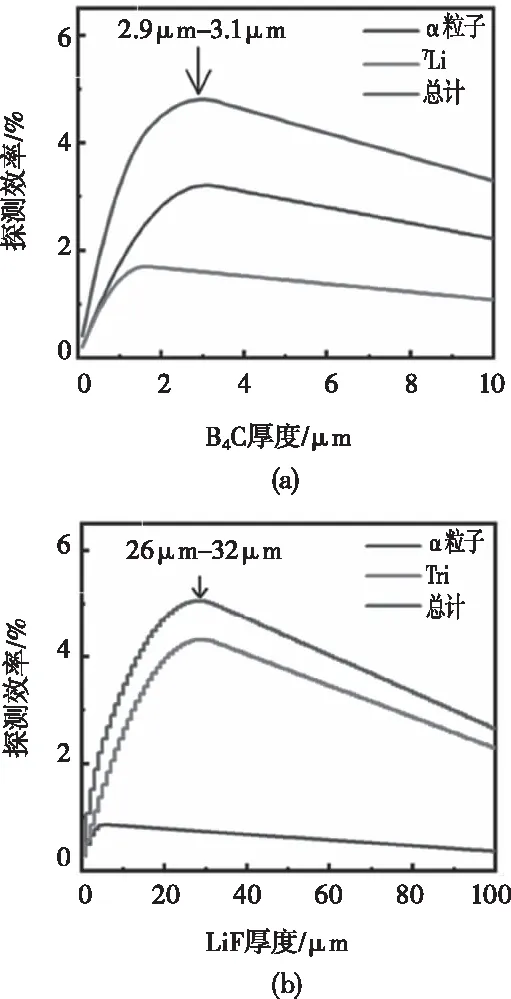
图10 理论分析计算的探测效率随转换层厚度的关系(a) B4C (b) LiF

从图7和10可知,理论分析计算结果与蒙特卡洛粒子输运计算得出的结果基本一致,热中子转化效率随B4C/LiF厚度呈先上升后下降的趋势,分别在2.9 μm～3.1 μm和26 μm～32μm时达到最大值(约4.8%和5.0%)。由于理论模型进行了一定程度的简化,因此该探测效率值与输运模型无法进行对比,但两种方法得出的最优厚度和趋势的一致性证明了输运模型的准确性。

5 结论

本文以利用聚乙烯慢化体和B4C/LiF中子转换材料测量252Cf中子为例,为提高对其的探测效率,建立粒子输运模型,并提出了一种全新的探测效率计算方式,优化了聚乙烯和转换层的厚度,同时指出对于单面涂转换层型探测器,应当将涂层面朝向中子入射方向以提高探测效率,最后从理论分析推导的角度验证了模型的准确性。本文的计算模型也可推广应用到其它中子场中子测量实验的关键参数选取,对于不同慢化体和热中子转换材料的优化设计均具有借鉴意义,为热中子探测器设计提供理论和数据支撑。下一步可以从实验角度来对关键参数进行验证性测试。