基于DebtRank算法的银行系统性风险仿真研究

范 宏,庞琮远

(东华大学旭日工商管理学院,上海 200051)

1 引言

自2007年次贷危机爆发并引发全球金融危机以来,金融系统性风险引起了国内外监管机构和学者的广泛关注,但目前的研究大多是从单一传染渠道的视角出发的,这在一定程度上低估了金融系统性风险。在金融系统中,从传染渠道的视角可以将其分为直接传染和间接传染两种,直接传染渠道主要是对银行间同业拆借市场进行系统模型构建,而间接传染渠道主要是对银行共同持有相同类型资产进行系统模型构建。

直接传染渠道中,国外最早进行这方面研究的是Allen和Gale[1],他们在研究系统性风险和市场结构关系时,发现完整的债权结构要比不完整的更稳定。Iori等[2]研究发现同质银行系统要比异质银行系统更加稳定。Gai和Kapadia[3]以同业拆借市场为主,探讨了传染性的可能性如何受到冲击类型、网络结构和资产市场流动性的影响,他们发现系统呈现出“稳健而脆弱”的特征。Sun[4]在银行同业拆借系统中发现流动性的增加会导致蜂拥效应。Karimalis和Nomikos[5]利用条件风险价值(CoVaR),分析了银行规模、杠杆和股票β值对系统风险贡献的关联程度,发现主要宏观经济变量的变化可以显著影响系统性风险。Giglio等[6]分析了欧洲19种系统性风险度量指标,发现杠杆在某些情况下对宏观经济下行风险具有较强的预测能力。国内一些学者对直接传染渠道也进行了相关研究,黄玮强等[7]综合运用最大熵和最小密度法间接推断的银行借贷关联网络来分析系统重要性和抗风险能力,研究发现,由最小密度法生成的网络中的银行违约风险传染更广、传染强度更大。唐振鹏等[8]基于支持向量机提出PSO-SVM-Copula-CovaR (PSCC)模型,使得在评估系统重要性银行上更加合理。冯超和王银[9]在银行同业市场的基础上构建服从马尔可夫决策过程的清算序列,研究系统风险爆发后最优的救助策略,针对系统性风险监测、存款保险制度和监管部门跨境处置合作提出了三点建议。

间接传染渠道中,国内外学者对此从不同角度展开研究并取得了一定成果。Caccioli等[10,11]构建了双边银行-资产网络,研究了杠杆、分散投资等对金融系统稳定性的影响,发现在系统中存在阈值,当高于该值时传染概率和传染强度会明显增强。Greenwood等[12]计算了银行在整个系统范围内的去杠杆化的敞口,以及各个银行引起的溢出,发现在持有共同资产的网络中传染风险主要来自资产贬值。Feinstein[13]基于持有共同资产的降价出售研究了银行系统性风险的特征,并提出了一种用于计算最大清算付款和价格的算法。姚鸿等[14]通过构建银行破产边界的数学模型,研究了银行个体风险、系统性风险,发现越相似的投资组合越容易引发系统性风险,降低银行杠杆率和银行间拆借比例可以有效的控制系统性风险。吴宜勇等[15]研究了资产价格波动对银行违约的影响,发现共同资产销售的间接效应远大于资产关联的直接效应。范宏和刘春垚[16]在间接传染模型的基础上加入组合相关性进行研究,发现资产之间的正相关关系加剧了金融传染,而负相关关系缓冲并抵消了冲击影响。

在实际金融系统中,直接传染和间接传染是同时存在的。国内外现有文献中将二者结合起来共同研究还比较少见。近期一些学者对此有所关注,Zhou Yichen和Li Honggang[17]同时考虑了银行借贷和持有共同资产,研究发现,金融系统具有资产多样化的“稳健而脆弱”。隋聪等[18]研究了债务与资产关联的叠加效应,发现叠加效应是形成银行系统性风险的主要推手。姜闪闪和范宏[19]等通过构建双渠道网络模型,引入宏观经济波动带来的投资风险,研究发现平均储蓄量、储蓄波动幅度等因素对银行系统稳定性有较大影响。

虽然目前对系统性风险的研究取得了一些较多的成果,但是,目前的研究还存在一定的问题,首先,目前大多数的研究以银行倒闭的数量来判定银行系统性风险,但是,现实世界中,发生银行倒闭的事件很少,很难用银行倒闭的数量来判定银行系统性风险。而债务等级法的判定,不需要有银行倒闭,就可以用来衡量整个银行系统的系统性风险,而采用债务等级法(DebtRank算法)来判定银行系统性风险的研究还缺乏。其次,在单一渠道下的研究中发现,杠杆、平均连接度对银行系统的传染具有很大的影响[5,6,10,14,20,21],但是,在双渠道传染下,杠杆、平均连接度对银行系统的系统性风险影响还未见。因此,本文首先构建双渠道传染模型,引入债务等级评价法用于判定银行系统性风险,然后研究杠杆、平均连接度对银行系统的系统性风险的影响。本文的研究可以为中央银行的政策制定提供一定的决策依据。

2 基于DebtRank算法的“双渠道”银行网络系统风险模型构建

2.1 双渠道银行网络系统风险传染模型

考虑一个由N家银行组成的拆借网络和N家银行和M类资产组成的投资网络,在图1中银行间的拆借关系用矩阵B表示,其中,Bij=1或Bij=0。Bij=1表示银行i、j之间存在拆借关系,Bij=0表示银行i、j之间不存在拆借关系。银资间的投资关系用矩阵Q表示,其中,Qiu=1或Qiu=0。Qiu=1表示银行i和资产u之间存在投资关系,Qiu=0表示银行i和资产u之间不存在投资关系。拆借矩阵B为银行间的网络结构,可以是随机网络,也可以是小世界网络、无标度网络等,本文参考Iori等[2]的做法,构建随机网络,投资网络Q同样为随机网络。网络中平均每家银行持有资产数可以用平均连接度μa表示

图1 双渠道金融系统风险传染网络模型

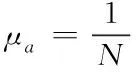
(1)

式(1)中,li表示第i家银行持有资产数。同理,网络中平均每家银行与其它银行发生拆借关系数可以用平均连接度μb表示

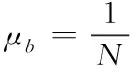
(2)

式(2)中,gi表示第i家银行与其它银行发生拆借关系数。同理,网络中平均每类资产被银行所持有数可以用连接度μf表示

(3)

式(3)中,lk表示第k类资产被银行所持有数。在投资网络中银行和资产是相互连接的,所以银行总的连接度和资产总的连接度是相等的,即μaN=μfM。

作为金融网络中的节点,银行的资产包括银行间贷款IA(流动性资产)、外部资产A(非流动性资产)和现金C,银行的负债包括存款D、银行间借款IL和所有者权益E,那么,资产负债表的平衡等式可以表示为

IA+A+C=D+IL+E

(4)

那么,银行i的杠杆可以表示为:

(5)

2.2 基于DebtRank算法的系统性风险定义

在双渠道金融系统中,若一家银行违约,一方面会通过拆借网络把压力传染给与其相连的银行,另一方面会通过投资网络把压力传染给与其相连的资产。在下一个时间步里,受到压力传染的银行会重复上面的过程,同时,受到压力传染的资产会把压力传染给与其相连的银行,因此,有的银行会受到来自银行和资产两方面的压力。如果有新的银行因冲击过大而违约,违约银行的压力传染会重复之前的过程,如此演化,金融系统初始受到的冲击会不断在系统中传播。

在此本文引进DebtRank算法的压力传染机制来刻画银行系统的系统性风险。参考Silva等[22]的做法,通过影响因子来反映银行或资产受到的压力冲击,本文将银行j对银行i的影响因子定义为

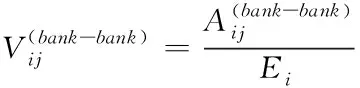
(6)

本文将银行j对资产k的影响因子定义为

(7)

本文将资产μ对银行i的影响因子定义为

(8)

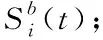
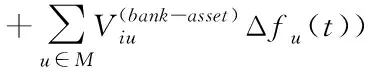
(9)

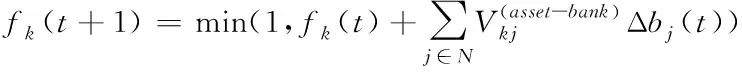
(10)

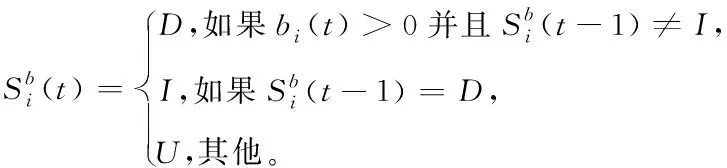
(11)

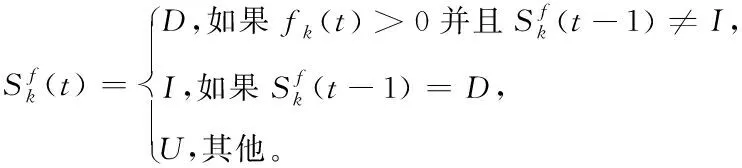
(12)

式(9)中,Δbj(t)=bj(t)-bj(t-1),Δfu(t)=fu(t)-fu(t-1)。式(11)(12)中的s是一个状态集合,包括压力状态D、不活跃状态I和活跃状态U,其中状态D表示银行或资产遭受冲击陷入困境,仍具备传播压力的能力,状态I表示银行或资产不活跃,不再具备传播压力的能力,状态U表示活跃,没有受到压力冲击。

本文采用债务等级DR来表示金融系统的系统性风险,其定义为

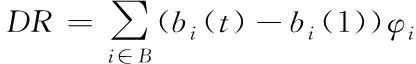
(13)

式(13)中,φi表示银行i的风险资产与系统风险总资产的比值,DR值越大,表明金融系统的系统性风险越大。

2.3 双渠道银行系统风险动态演化流程

当金融系统受到外部冲击时,金融压力会沿着直接传染和间接传染两条渠道进行传播,其动态演化流程如图2所示:

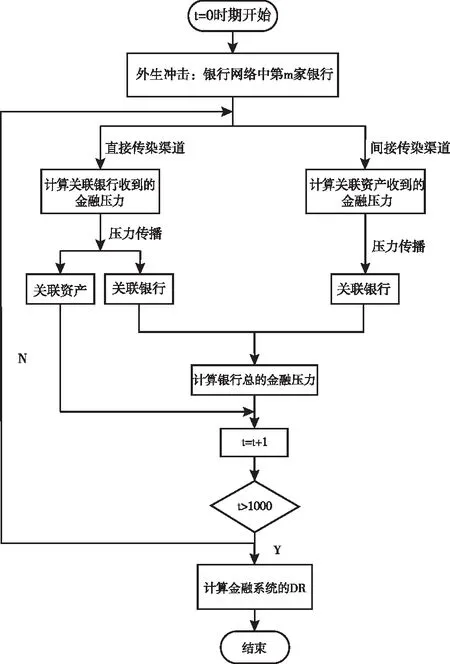
图2 双渠道动态演化流程图

步骤1:设定初始仿真值;

步骤2:给定一个外生冲击(假设随机一家银行违约);

步骤3:计算受到外生冲击的银行和资产的压力;

步骤4:有压力的银行会把压力通过直接传染和间接传染渠道传播给与其关联的银行和资产,有压力的资产会把压力通过间接传染渠道传播给与其关联的银行;

步骤5:计算同时受到直接和间接传染影响的银行的金融压力;

步骤6:当时间步不满足于大于1000时,重复上述计算过程;

步骤7:当时间步大于1000时,计算当前平均连接度下系统的DR值。

为了使得到的仿真结果更加稳定可靠,本文在每个连接度下都进行了1000次仿真。

3 仿真计算

3.1 仿真参数设置

本文采用MATLAB 2018a软件进行仿真研究。假设在金融系统中,银行数N=100,资产数M=100,仿真时间步t=1000,特别地,在该金融系统网络中,银行数与资产种类数的绝对值并不影响系统的状态特征,当银行数与资产种类数无穷大时,其比值是一定的。假设系统中的每家银行及资产规模相同,每家银行将可投资和拆借的资产平均分配给其拥有的投资组合,初始资产总额S=80,银行间的拆借网络和投资网络随机生成。为保证实验结果的稳定性,仿真次数设置为1000。本文考虑杠杆(λ)、平均连接度(μ)等因素进行仿真研究。

3.2 双渠道下杠杆对金融系统的系统性风险影响

金融系统中,杠杆表示银行的风险总资产与所有者权益的比值,即风险的大小。本文在不同平均连接度下研究双渠道中杠杆对金融系统稳定性的影响,如图3所示。从图3中的仿真结果可知:双传染渠道下系统性风险会随杠杆的增加而不断增大,说明杠杆对金融系统的系统性风险具有单调增加的作用,但不同传染渠道占优下的增速是不一样的,直接传染渠道占优随杠杆增加的最快,间接传染渠道占优随杠杆增加的最慢,说明在双渠道金融系统中,可以通过减少银行间的拆借(即直接传染渠道资产占比)来提高系统稳定性,或者说,在双渠道金融系统中,银行间同业拆借资产占比越大时去杠杆化效果越好。但在相同平均连接度下可以发现,随着杠杆的增加,拆借和投资资产占比不同的双传染渠道之间会产生一个阈值,使得阈值左右不同传染渠道占优对系统稳定性影响的位次发生变化,说明在双渠道金融系统中,平均连接度不变的情况下,可以通过同时调节杠杆和拆借和投资资产占比来实现系统性风险最小化,而且,随着平均连接度的增加,阈值也随之不断增大(从图3(b)-图3(f)看出,阈值在变大),但金融系统的债务等级却不断减小,说明平均连接度高具有分散系统性风险的作用在双渠道金融系统中同样适用。

3.3 双渠道下平均连接度对金融系统的系统性风险影响

连接程度是指银行与其它银行或资产直接相连的个数。平均连接程度是对连接程度所求的一个均值。本文在不同杠杆值的状态下研究双渠道中平均连接度对金融系统稳定性的影响,结果见图4。由图4中的仿真结果可知:当金融系统是投资资产占比更大时,系统的债务等级随着平均连接度的增加而增大,说明在双渠道金融系统中间接渠道占优对系统性风险具有单调增加作用;当银行间拆借资产占比更大时,系统的债务等级随着平均连接度的增加先瞬间增大再不断减小,说明双渠道金融系统中直接渠道占优下较小的平均连接度对系统性风险单调增加,但超过临界值平均连接度就会对系统性风险单调减少。在相同杠杆下,当系统的平均连接度较小时,银行间拆借资产占比更大对系统造成的不稳定性越高,但随着平均连接度的增加,投资资产占比更大的双渠道金融系统造成的不稳定性会在某一个阈值下超过拆借资产占比更大的双渠道金融系统(如图4(a),图4(b),图4(c)),而且,随着杠杆的增加,不同传染渠道之间的阈值会随之增大(图4(e)和图4(f)由于阈值较大,大到连接度超过50的情形),说明在杠杆较大的系统中,监管机构需要更加关注直接传染渠道给金融系统带来的影响。

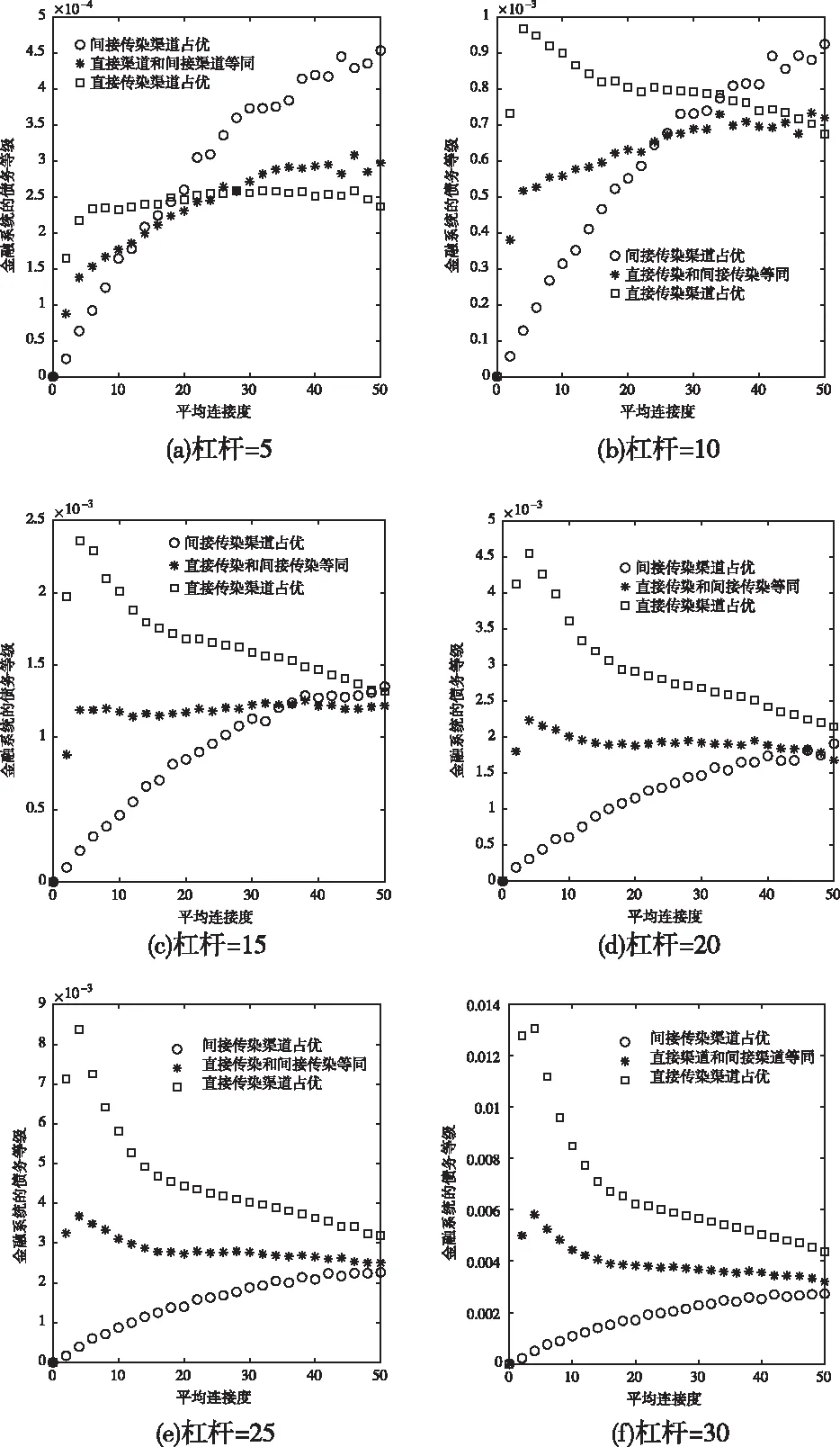
图4 双渠道中平均连接度对金融系统稳定性的影响

4 结论

本文通过构建双渠道网络传染模型讨论了杠杆和平均连接度对系统性风险的影响,并进一步探究了不同渠道下的传染机理,从金融系统传染渠道的角度为降低系统性风险提供了一定参考,仿真结果得到了以下几个重要结论;首先,杠杆对银行系统性风险的影响具有单调增加的作用,并且直接传染渠道占优下(即银行间拆借资产占比更大)杠杆发挥的单调增加作用更强;平均连接度对间接传染渠道占优下(即银资间投资资产占比更大)的系统性风险具有单调增加的作用,而直接传染渠道占优下只有当其较小时才具有单调增加的作用。第二,双渠道金融系统中杠杆和平均连接度对系统性风险的影响并不是一呈不变的,而是会随杠杆和平均连接度的增加产生一个阈值;在平均连接度不变的情况下,当杠杆小于阈值时,间接传染渠道占优对金融系统性风险的影响高于其它两种情况,当杠杆大于阈值时,直接传染渠道占优对系统性风险的影响更大;而在杠杆不变的情况下,随着平均连接度的变化情况则恰恰相反,小于阈值时,直接传染渠道占优影响更大,大于阈值时,间接传染渠道占优影响更大。本文的研究结果明确了双渠道下杠杆和平均连接度对银行系统性风险的影响,对中央银行的政策制定提供一定的决策依据,为监管部门监测和调节金融系统提供一定的参考意义。此外,本文的研究是基于随机网络下的金融系统,未来可以考虑用最大熵或最小密度的方法来构建金融网络,并进一步搜集实际数据来进行实证研究。