顾及路口压力的A2C交通信号调控
张 蕾,郭全盛,林建新,李建武
(1. 北京建筑大学电气与信息工程学院,北京 100044;2. 建筑大数据智能处理方法研究北京市重点实验室,北京 100044;3. 北京建筑大学土木与交通工程学院,北京 100044;4. 北京理工大学前沿技术研究院,北京 100081)
1 引言
近年来,随着城市的不断扩张以及人口的快速增长,全球大都市中的交通运输需求急剧提升。超大规模的交通流量给现有基础设施带来巨大压力,导致严重拥堵,加剧了碳排放污染,给城市规划、社会稳定带来负面影响。缓解城市交通拥堵是国家“十四五”规划中加快建设交通强国的重点和难点,是刻不容缓的。城市交通车流量变化之间有着复杂且紧密的联系,通过有效调控,疏导车辆选择合适的通行线路,为有关部门提供科学的决策支撑,进行有针对性的交通疏导,提高通行效率和经济效益。
自适应交通信号控制(Adaptive Traffic Signal Control,ATSC)旨在根据交通现状实时调控交通信号灯的变化,缓解交通路网中存在的交通拥堵现象,提升车辆通行效率。在网格状的路网中,如在车流量密集的市中心区域,传统的多道路交叉口控制方法通过在所有交叉口之间设置固定偏移量实现协调控制,最经典的是FixedTime算法[1],该算法设置了随机偏移量和固定的信号变化时间。此外,美国交通运输委员会与美国联邦公路局编写的信号控制手册中也采用了类似方法[2]。然而,上述方法过于简单,现实交通网络难以达到理想状态,很难通过固定偏移量进行全局优化。
针对此缺陷,研究人员提出基于优化的算法,最常见的是基于马尔可夫决策过程(Markov Decision Process,MDP)的强化学习(Reinforcement Learning,RL)算法,用于对真实世界的交通量进行动态调控[3]。例如,Wei等[4]提出基于强化学习的IntelliLight模型,使用深度Q网络(Deep Q Network,DQN)对交通环境进行分析,进而预测交通信号灯的下一个状态。近年来,强化学习领域的重要分支——Actor-Critic (A2C,演员-评论家)算法被广泛用于ATSC中,并通过深度神经网络(Deep Neural Network,DNN)来模拟A2C的策略和状态[5]。Hua等[6]提出了CoLight模型,使用图注意力网络结合相邻交叉点之间的影响,用于对多个交通信号灯进行控制。Chu等[7]提出了多智能体A2C模型(Multi-agent A2C,MA2C),将深度神经网络与多智能体强化学习(Multi-agent Reinforcement Learning,MARL)结合,在交通信号控制领域中得到了较好的实验效果。然而,以上算法的表达能力易受策略设计的影响,即错误的策略反而降低交通调控的效果。
2 相关工作
2.1 强化学习算法

强化学习主要分为三类:基于价值的方法(value based)、基于策略的方法(policy based)和演员-评论家算法(Actor-Critic,A2C)。由于A2C算法既可以处理高维连续的行动,又可以单步更新快速学习,因此,在具有线性回归智能体的ATSC中,A2C算法的表现优于前两种[10]。


(1)


(2)
2.2 多智能体Actor-Critic算法
在多智能体网络G=(V,ε)中,V是节点集,ε是路径集。如果节点i和j之间存在边,则称它们为邻居节点。i的邻居节点定义为Ni,本地区域定义为Vi=Ni∪i。此外,d(i,j)为连接任意两个智能体之间的最小边数。
在多智能体Actor-Critic算法 (Multi-agent Actor-Critic,MA2C)中,首先,提取邻居节点的策略信息,用来提高每一个智能体的可观察性;其次,提出空间折扣因子,削弱来自其它智能体状态和奖励的信息。在智能体之间联系有限的情况下,从邻居智能体之间抽样最新策略πt-1,将Ni=[πt-1,j]j∈Ni作为深度神经网络的输入,此时,当前状态为st,Vi。局部(local)策略公式如下
πt,i=πθi(·|st,Vi,πt-1,Ni)
(3)
其中,πθi为第i个智能体采用策略梯度算法直接用参数化模型拟合的策略[11]。由此,局部智能体将接收到实时的最近邻居智能体的策略。这是基于两个交通控制事实:首先是交通状态在短时间内变化缓慢,因此,当前步骤策略与最后一步策略非常相似;其次是在当前的状态和策略下,交通状态的动态变化符合马尔科夫决策过程。
虽然局部智能体知道局部区域状态和邻域策略,但难以通过局部的价值回归来拟合全局回报。为了达到全局合作的效果,假设全局奖励分解为rt=∑i∈Vrt,i,引入空间折扣因子α,调整智能体i的全局奖励
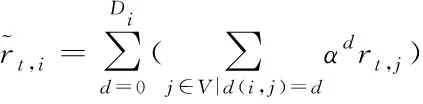
(4)
其中,Di是与智能体i之间的最大距离,α类似于强化学习中的时间折扣因子γ,此处是按照空间顺序而不是时间顺序按比例缩小信号,折扣全局奖励在贪心控制(α=0)和合作控制(α=1)之间得到平衡,且与估计局部策略πθi的优势更相关。使用α将邻居状态转化为

(5)

(6)
其中,Vωi是智能体学习到的价值函数。价值损失式(2)变为

(7)

(8)

3 顾及路口压力的多智能体Actor-Critic算法
为了避免传统强化学习中各智能体之间缺乏联系、算法策略不佳等问题,提出顾及路口压力的多智能体Actor-Critic算法(Intersection Pressure-based Mulit-agent A2C,IPMA2C)。首先,基于顾及路口压力的强化学习策略对交通路口进行分析,通过缓解压力的方法对路网进行优化;其次,构建基于深度神经网路的多智能体Actor-Critic模型,提升交通调控能力。
3.1 基本定义
1) 交通路口的进车道、出车道
交通路口的进车道是车辆进入交通路口的车道,交通路口的出车道是车辆驶出该路口的车道。将交通路口的进车道集合表示为Lin,出车道集合表示为Lout。
2) 交通运动
交通运动定义为汽车从一个进车道通过一个交通路口行驶到一个出车道。将通过一个交通路口的交通行为表示为(l,m),其中,l是进车道,m是出车道。
3) 运动信号、相位
以交通路口信号控制车辆的运动,其中,绿灯表示允许移动,红灯表示禁止移动。将运动信号定义为a(l,m),其中,a(l,m)=1表示绿灯,即允许运动(l,m),a(l,m)=0表示红灯,即禁止运动(l,m)。相位是运动信号的组合,定义为p={(l,m)|a(l,m)=1},其中,l∈Lin,m∈Lout。
4) 运动压力、交通路口压力


(9)
如果所有车道的最大容量xmax相同,则w(l,m)只表示进出车辆数量之间的差异。
交通路口i的压力定义为所有交通运动的绝对压力之和

(10)
压力Pi表示车辆进出密度的不平衡程度,Pi越大,车辆分布就越不平衡。
因此,将多路口交通信号调控问题描述为:每个路口都由一个强化学习智能体来控制交通信号灯,在每个时间步t内,智能体i从环境中观察到自己的状态。给定车辆分布和当前信号阶段,智能体的目标是采取最优动作at,i(即交通路口的信号灯进入哪个阶段),从而获得最大奖励(即所有车辆的平均行驶时间最短)。
3.2 智能体
1) 状态(State)
状态是为一个单独的交通路口定义的,即多智能体强化学习中智能体观察到的内容,包括该交通路口i在t时刻每个进车道的车辆数xt,i(l)(l∈Lin,i),及在t时刻出车道的车辆数xt,i(m)(m∈Lout,i)。状态表示为
st,i={xt,i(l),xt,i(m)}l∈Lin,i,m∈Lout,i
(11)
其中,l是交通路口i的进车道,m是交通路口i的出车道,Lin,i是进车道的集合,Lout,i是出车道的集合。
2) 动作(Action)
在t时刻,每个智能体从动作集A中选择一个动作at,i作为该阶段的动作,即信号接下来的状态。每个智能体有四个动作,分别为东西直行,东西左转,南北直行,南北左转,如图1。

图1 动作定义图
图1中,(a)东西直行 (b)东西左转 (c)南北直行 (d)南北左转
3) 奖励(Reward)
定义智能体i的奖励为
rt,i=-Pt,i
(12)
其中,Pt,i是第i个交通路口在t时刻的压力,即进出车道上车辆密度之间的不平衡程度。通过最小化Pt,i,使路网内的车辆可以均匀分布,进而优化路网的车辆吞吐量。
3.3 IPMA2C模型
由于交通流是复杂的时空数据,如果智能体只知道当前时刻的状态,则马尔科夫决策过程可能会变得不稳定。最简单的方法是将所有历史状态全部输入到Actor-Critic算法中,但是会显著增加状态的维度,减少Actor-Critic对最临近交通状况的关注。LSTM可以保持隐藏状态并记住简短的历史信息[12],因此,本文将LSTM作为隐藏层,从输入中提取信息。
IPMA2C模型如图2所示。首先,状态和邻居策略分别输入到全连接层FC;然后,利用LSTM作为最后一个隐藏层从状态中提取特征;输出层连接Actor-Critic算法的Actor和Critic两部分,其中Actor对应的是Softmax函数,Critic对应的是Linear函数。采用正交初始化[13]和RMSprop[14]作为梯度优化器。对于每个输入的状态,采用贪婪策略收集交通环境的统计数据。为防止梯度爆炸,所有归一化的状态被缩放到[0,2]范围内,且每个梯度的上限为40。类似,将奖励归一化并缩放到[-2,2],以稳定小批量更新。

图2 IPMA2C模型
4 实验分析
4.1 实验设置
基于SUMO[15]平台,生成由25个交通路口和信号灯构成的模拟交通网络,如图3。该网络由限速20m/s的双车道主干道组成,其中,交通路口间的距离为300m。每个路口的动作包括:东西直行、东西左转、南北直行和南北左转四种,车辆可以自主右转。设F1={x4->x10,x5->x11,x6->x12}(东->西),F2={x1->x7,x2->x8,x3->x9}(北->南)为两组车辆起点至目的地(Origin-Destination,OD)的集合。

图3 包含25个路口的5×5模拟交通网络图,圆圈内为示例交通路口
初始状态,大量车流从F1的起点不断生成,少量车流从F2的起点生成。15分钟后,F1生成少量车流,F2则变为生成大量车流,由此循环往复。通过生成大量的车流以产生交通拥堵,检测IPMA2C模型在交通疏导方面的能力。
为了在模型运行时间Ts内模拟交通环境,定义Δt为强化学习中智能体与交通环境之间的交互周期。如果Δt太长,智能体无法对路网产生有效调控;如果Δt太短,智能体的即时决策将无法按时传达。此外,如果交通灯的控制切换过于频繁,则会存在安全隐患。设Ts=3600s,Δt=5s。对于马尔科夫决策过程,设γ=0.99,α=0.75,奖励系数a=0.2veh/s,状态和奖励的归一化因子分别为5veh和2000veh;对于IPMA2C模型,设minibatch的大小|B|=120,β=0.01。
为了验证IPMA2C模型的效率和稳定性,将其与传统的经典交通控制模型进行对比。选取的基准模型如下:
1)具有随机偏移量和固定变化时间的FixedTime方法[1];
2)对车辆等待时间和队列长度进行优化的多智能体Actor-Critic算法(MA2C)[7];
3)学习智能体之间互相影响和联合动作的CoLight算法[6]。
4.2 实验结果
图4为IPMA2C模型与其它基准模型在一个小时内到达目的地的车辆数量变化情况。在开始的前15分钟,IPMA2C模型并未展现出优势,这是因为虽然有大量车流进入路网,但尚未造成严重拥堵,此时,传统交通控制方法均可实现良好的调控。随着路网中车流量越来越大,IPMA2C模型的优势开始逐渐显现,最终,有更多车辆到达目的地,性能优于其它模型。

图4 车辆到达数量对比图
图5为网内车辆平均速度的变化情况。在前15分钟,即没有拥堵时,四种模型的平均车速均逐渐上升。当产生严重拥堵时,四种模型的平均车速均开始下降。但在整个过程中,IPMA2C模型的平均车速均高于其它三种模型,体现了最优性能。

图5 平均速度对比图
表1为其它评价指标的统计结果,IPMA2C模型提升了交通调控效率。其中,车辆的平均行程时间缩短了至少5%,平均行程等待时间缩短了8%,平均行程时间损失缩短了7%,而平均行程速度提升了至少6%。这些实验结果均表明IPMA2C模型的性能优于其它基准模型。

表1 实验结果统计表
相比其它方法,IPMA2C通过顾及路口压力的强化学习策略,对路口的状态进行分析,通过基于深度神经网络的Actor-Critic算法对交通信号进行调控。顾及路口压力的强化学习策略,将关注重心放在减少路口等待车辆的数量上,而非缩短车辆等待时间;在基于深度神经网络的Actor-Critic模型中,全连接网络FC有强大的特征提取能力,LSTM作为隐藏层具有长时记忆的能力,可以保留历史信息。因此,在缓解拥堵方面有更好的效果,性能也是最好的。
5 结束语
本文提出一种新颖的顾及路口压力的多智能体Actor-Critic算法,用于对交通信号进行智能调控,缓解了交通拥堵。首先,设计更合理的顾及路口压力的强化学习策略;其次,提出基于深度神经网络的IPMA2C模型;最后,在模拟交通网络中验证IPMA2C模型的鲁棒性、最优性,其性能优于其它传统的基准算法。
在未来工作中,将研究更先进的策略优化模型,并尝试将其推广到交通路口数量更多、路网更复杂的真实环境中进行测试。

