功能梯度压电压磁圆柱壳中纵向波的截止频率1)

邓良玉 曹小杉 马星荃 汝 艳

(西安理工大学土木建筑工程学院,西安 710048)

引言

功能梯度材料是由两种或两种以上材料组成,其成分和结构沿某一方向连续梯度变化的非均质材料.相比于传统的均质弹性材料,功能梯度材料具有耐高温、减小残余应力等优势,随着各种新型材料的发现,功能梯度材料技术不仅应用于弹性材料中,也应用于压电材料、压磁材料和压电压磁材料等材料当中.压电压磁材料是一种力电磁耦合材料,在智能结构和智能材料领域有着广泛的应用,可以用来制作传感器[1]和换能器[2]等精密电子元件.一方面,可以将功能梯度的概念引入到压电压磁材料中,制备出材料参数渐变的力电磁耦合材料,以期获得更好的性能,可以应用于各类换能器、传感器及各类声波器件中.另一方面,材料由于亚表面的老化、损伤和腐蚀等原因会导致材料特性出现渐变特性,采用功能梯度压电压磁材料模型可以表征含渐变梯度损伤后的压电压磁材料结构的材料特性.因此功能梯度压电压磁材料及结构中的静、动力学行为成为智能材料结构力学研究热点之一.

基于高性能声波器件的结构无损检测的两大类应用需求,研究者关注对不同结构中的弹性波的传播.近些年来,对于弹性波的研究多集中在棒[3]、板[4]、壳[5]和半空间[6]等结构上,例如压电纳米半空间结构中的表面波[7]、密度梯度对圆柱壳中弹性波波形的调控作用[8]和黏弹性梯度层中的瞬态波[9]等等.压电压磁材料及其结构中的弹性波也得到研究人员的关注,Li 等[10]分析了理想界面磁电层状结构中外部磁场对结构中SH 波位移、应力、电势和磁势的影响.Pang 等[11]和赵星等[12]分别讨论了非理性界面的磁电板状结构和半空间结构中电磁边界条件对SH 波频散的影响.Kumari 等[13]揭示了多层压电圆柱壳中壳体厚度、初始应力等对SH 波相速度的影响规律.孔艳平等[14]讨论了磁电弹板中厚度-扭转波的位移、电势和磁势.上述文献的研究内容大多集中在弹性波的频散特性、波结构分析.

截止频率是弹性波的重要特性之一,在工程上具有广泛应用,可用于超声无损检测[15]、测量结构厚度[16-17]、传感器[18]和滤波器[19]等当中.通常针对各类半空间结构,由于需满足无穷远处衰减条件,其弹性导波有速度上限.此时弹性导波的不同模态的截止频率对应的是弹性波速达到波速上限值的情况[20].而对于有限厚度结构(如板、壳)中,弹性导波的波速无上限,其截止频率对应为波数趋近于零的情况.通常,研究非均质有限厚度结构中弹性导波截止频率时,可以采用直接求解法,即采用解析[21-22]或者数值方法[23]求得波的频散曲线并由此分析频散曲线中波数趋近于零的情况.均质板的Lamb 波与SH 波的截止频率解析解答均采用直接求解法得到[24].如果材料为非均质材料,波动方程为变系数偏微分方程组,解析求解较困难,因此多采用数值方法求得频散曲线.解析求解场方程的方法主要有特殊函数法[25]、幂级数方法[22]和勒让德级数法[26]等.特殊函数法仅限于材料参数按照某些特殊规律变化的情况,而幂级数法和勒让德级数方法的本质是渐近解析解,无法给出简单形式的显式解答.Cao 等[27-28]在研究功能梯度板中的SH 波[27]和Lamb 波[28]的截止频率时发现,可以仅讨论波数趋近于0 的情况并简化方程,基于Wentzel-Kramers-Brillouin (WKB)方法获得弹性导波的显式解析解答,并与文献[21]中的传统直接求解法所得结论对比,可得到这些显式解答形式简单且具有足够的精度的结论.随后,周凤玺等[29]将该方法应用于梯度饱和多孔材料中弹性波的截止频率,并进一步论证了该解答的精确性[29].基于这些方法,研究已拓展至压电压磁圆柱壳中环向SH 波的截止频率[30]、压电准晶体圆柱壳轴向波截止频率[31]、偏心圆柱中导波的截止频率[32]和压电圆板自由振动的截止频率[33]等多个方向.

本文研究了内外表面无应力和电磁开路条件下功能梯度压电压磁圆柱壳中纵向导波的截止频率.首先,令波数趋近于零并简化波动控制方程组;然后利用齐次边界条件将控制微分方程组解耦为两个独立方程;进一步采用WKB 法分别求解两个独立方程并将解代入边界得到截止频率显式表达式和简化形式;分别与均质壳体中的贝塞尔函数解和功能梯度结构中的传统方法进行对比分析,验证了WKB解的精确性;最后研究了材料参数梯度组成方式、参数梯度变化及圆柱壳体厚度变化对截止频率的影响,以期为基于截止频率的非均质材料圆柱结构的超声无损检测提供理论依据.

1 基本方程

设如图1 所示功能梯度横观各向同性压电压磁圆柱壳,其中roθ 面为各向同性面,极化方向沿z轴正向.圆柱壳内径为Ra,外径为Rb,材料参数沿径向连续变化,是坐标r的函数.对于沿壳体z轴方向传播的纵向导波,其周向波数为0,即位移、电势和磁势函数与 θ 无关.那么,柱坐标系下位移、电势和磁势函数可表示为

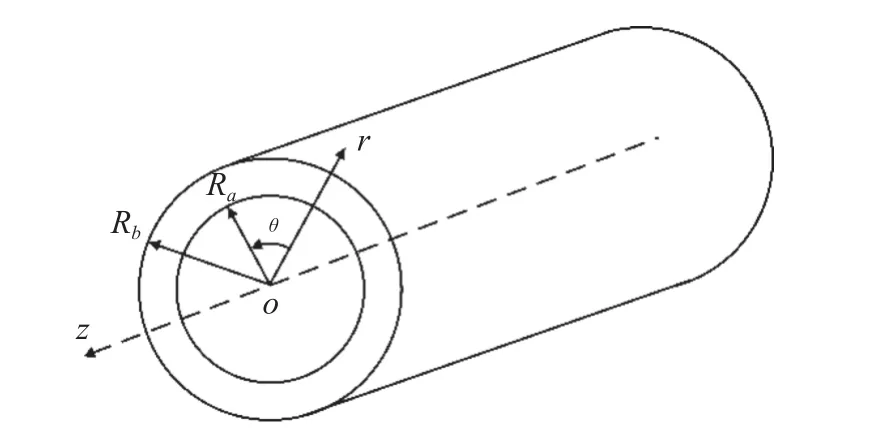
图1 功能梯度压电压磁圆柱壳Fig.1 An FGPPM cylinder shell

其中,u,w分别为径向和轴向位移函数,φ表示电势函数,ψ代表磁势函数.

应变与位移的关系为

其中,Srr,Sθθ,Szz和Srz为应变分量.

电场强度与电势的关系为

其中,Er和Ez为电场强度分量.

磁场强度与磁势的关系为

其中,Hr和Hz为磁场强度分量.

横观各向同性压电压磁材料的本构方程为

其中,σrr,σθθ,σzz和 τrz为应力分量;Dr和Dz为电位移;Br和Bz为磁感应强度;c11,c12,c13,c33和c44为弹性系数;e15,e31和e33为压电系数;ε11和 ε33为介电系数;f15,f31和f33为压磁系数;g11和g33为磁电系数;µ11和 µ33为磁导率.如果材料为功能梯度材料,上述材料参数都是坐标r的函数.

柱坐标下的运动方程为

其中,ρ 是材料密度,也是坐标r的函数.

电位移平衡方程为

磁感应平衡方程为

将式(2)～式(4)代入式(5),再把新的方程代入式(6)～式(8)得到场控制偏微分方程组

其中,“ ′ ”表示对r的导数.

2 问题求解

对于在圆柱壳轴向传播的纵向波,其试探解可设为

其中,U(r),W(r) 分别代表径向和轴向位移幅值,Φ(r)代表电势幅值,Ψ(r)代表磁势幅值,i 为虚数单位,k表示波数,ω表示频率.

将波函数试探解式(10)代入式(9)中,偏微分形式的场控制方程组化为常微分方程组的形式

当k→0 时,常微分方程组可化为

其中,ωn表示截止频率.此时边界条件可以写为

式(14)和式(15)积分可得

其中,q1和q2是积分常数.结合式(20)、式(18)和式(19)可以得到

将式(21)代入式(13)可得

其中,cE是等效弹性系数,且

2.1 梯度圆柱壳体纵向导波截止频率的WKB 解

式(22)可以采用WKB 法进行求解,假设式(22)的解为

其中,设ϕ(r)可表示为

将式(23)代入式(22)得

求解式(26)得

忽略 ϕl,l＞1,从而得到式(23)的解

其中,C1和C2是两个待定常数.为等效剪切波波速的倒数.由式(17)～式(19)可知,位移函数w满足的边界条件为

将式(28)代入式(29)得

式(30)和式(31)存在非0 解的充分必要条件为C1和C2的系数矩阵行列式为0,进而可以得到

同样采用WKB 法对式(12)求解得

式中,C3和C4为待定系数,将式(33)代入边界条件式(16)并考虑非零解存在的充分必要条件得

ωnU是满足式(34)的截止频率解.

观察式(32)和式(34)可以发现,考虑到 ωnU和ωnW是数值较大的参数,当材料参数缓慢变化时,等式的右边趋近于零,因此可以简化为

可以写为

因此有

从式(37)可以看出,截止频率 ωnU和 ωnW可以看作两个近似的等差数列集.如果材料为均质材料,则截止频率为

2.2 均质圆柱壳体截止频率的Bessel 函数解

为对比验证WKB 解的精确性,本文给出均质圆柱壳体纵向导波的特殊函数解.当壳体退化为均质材料时,可以求得截止频率的精确解,此时式(12)变为

式(40)为Bessel 方程,求得解为

将式(41)代入式(16)中,考虑方程组非0 解存在的充分必要条件,令方程组系数矩阵行列式为0,得到

式(22) 可采用相同方法求解,可以得到关于ωnW的超越方程

3 数值算例

数值算例中,将讨论3 种材料.第1 种是均质材料,材料参数如表1 所示.第2 种材料是由已知的压电材料与压磁材料复合而成的功能梯度压电压磁材料.其中内表面为压电材料 BaTiO3,外表面为压磁材料 CoFe2O4,材料参数如表2 所示.除电磁系数为常数外,材料参数的梯度变化规律为

表1 一种均质压电压磁材料的材料参数Table 1 The materials parameters of homogeneous piezoelectric-piezomagnetic material

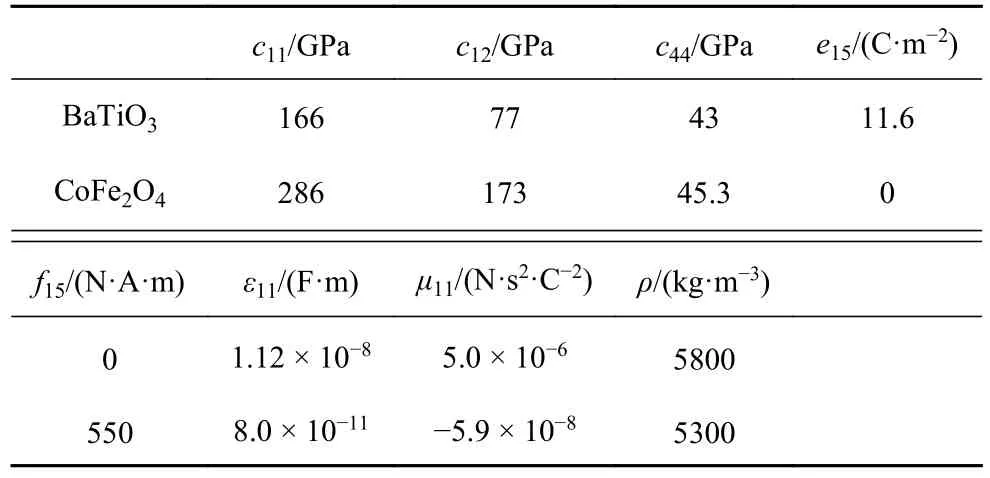
表2 BaTiO3 和 CoFe2O4 的材料参数Table 2 The materials parameters of BaTiO3 and CoFe2O4

其中,p为梯度参数,f(1)为BaTiO3的材料参数,f(2)为 CoFe2O4的材料参数,且

即圆柱壳内径为材料 BaTiO3,外径材料为 CoFe2O4.电磁系数选择为g11=5.0×10-12N·s·V·C.

第3 种为人工设定材料功能梯度,拟用以讨论不同材料参数梯度变化对截止频率的影响规律.这种材料在内径处,材料参数与表1 所示材料参数相同,有且仅有一个参数梯度变化,其他材料参数为0.材料参数变化规律满足

3.1 解的精确性验证

为了验证WKB 解的准确性,算例1 讨论均质压电压磁圆柱壳中纵向波的截止频率.其中,壳体内径Ra=9 mm,外径Rb=10 mm,材料参数同表1 中的参数.对比式(32)和式(34)给出的WKB 解与式(43) 和式(42) 得到的Bessel 函数解.计算结果如表3 和表4 所示.从两个表中可以看出,WKB 解式(32)和式(34)与简化的解式(39)和式(38)的结果是一致的;WKB解与Bessel 函数解得到的结果之间很相近,其中第1 阶模态之间的相对误差不超过0.05%,并且随着模态的增加,两者之间的相对误差也越来越小.

表3 均质压电压磁圆柱壳中纵向波的截止频率ωnW/MHzTable 3 The cut-off frequencies ωnW/MHz of longitudinal waves in a homogenous piezoelectric-piezomagnetic cylinder shell

表4 均质压电压磁圆柱壳中纵向波的截止频率ωnU/MHzTable 4 The cut-off frequencies ωnU/MHz of longitudinal waves in a homogenous piezoelectric-piezomagnetic cylinder shell

算例2 考虑采用传统的计算截止频率的方法,即求解方程(11)并代入边界条件,考察k→0 时的ω值.由于方程(11)为变系数常微分方程组,直接求解困难,该类问题的常见解法有勒让德级数法[26]和幂级数方法[22].截止频率的直接解法可以采用幂级数方法求得其渐近解,并得到频散方程.计算过程中选用第二种变化形式的功能梯度材料,取壳体内径Ra=9 mm,外径Rb=10 mm,计算k=0.001 时的频率值并与WKB 解对比分析,如表5～表7 所示.其中,利用WKB 法求解功能梯度压电压磁材料、均质压电材料和均质磁电材料圆柱壳体中纵向波的截止频率,可以得到两个序列的值,如表5 和表6 所示,两个序列模态由低至高用罗马数字编号.采用直接解法求得的截止频率为一个系列,对应模态用阿拉伯数字编号,如表7 所示.计算结果对比可得,两者计算结果几乎无差别.但显而易见,如采用渐近解法求得整体频散曲线并进而求得截止频率,计算量远远大于WKB 解,且不易发现其规律性.

表5 BaTiO3 圆柱壳、CoFe2O4 圆柱壳和FGPPM 圆柱壳中纵向导波的截止频率ωnW/MHz 的WKB 解Table 5 The cut-off frequencies ωnW/MHz of longitudinal waves in BaTiO3,CoFe2O4 and FGPPM cylinder shell

表6 BaTiO3 圆柱壳、CoFe2O4 圆柱壳和FGPPM 圆柱壳中纵向导波的截止频率ωnU/MHz 的WKB 解Table 6 The cut-off frequencies ωnU/MHz of longitudinal waves in BaTiO3,CoFe2O4 and FGPPM cylinder shell

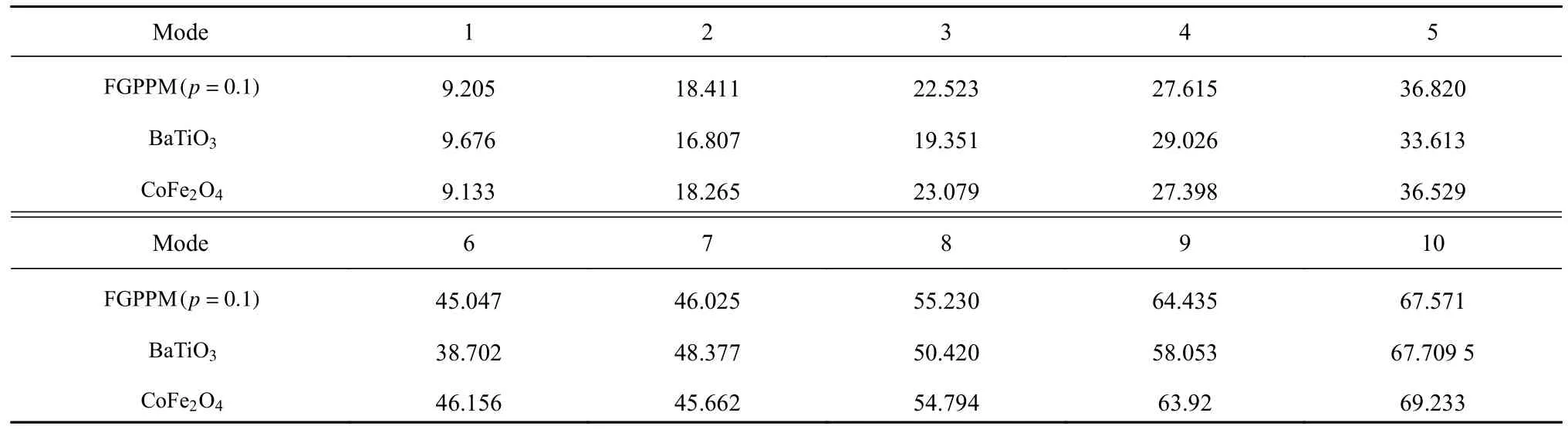
表7 BaTiO3 圆柱壳、CoFe2O4 圆柱壳和FGPPM 圆柱壳中纵向导波的截止频率(MHz)Table 7 The cut-off frequencies of longitudinal waves in BaTiO3,CoFe2O4 and FGPPM cylinder shell (MHz)

3.2 材料参数梯度变化对截止频率的影响

考察功能梯度压电压磁材料的不均匀性对纵向波截止频率的影响.首先观察算例2 中的计算结果,对比分析 BaTiO3圆柱壳、CoFe2O4圆柱壳和梯度参数p=0.1 的功能梯度压电压磁圆柱壳中纵向波的前5 阶截止频率 ωnW和 ωnU,如表5 和表6 所示.可以看到功能梯度压电压磁圆柱壳的截止频率介于BaTiO3圆柱壳和CoFe2O4圆柱壳之间.在同一阶模态,BaTiO3圆柱壳纵向波的截止频率 ωnW的值大于CoFe2O4圆柱壳的截止频率 ωnW的值,而 BaTiO3圆柱壳纵向波的截止频率 ωnU的值则小于 CoFe2O4圆柱壳的截止频率 ωnU的值.

进一步,讨论功能梯度压电压磁圆柱壳中纵向导波的截止频率与梯度参数p的关系,表8 和表9对比了p=0.1,0.2,0.3 这3 个不同值时纵向导波前5 阶截止频率的变化情况,可以看到随着p的增大截止频率 ωnW也随之增大,而截止频率 ωnU则随着p的增大而减小.

表8 不同梯度参数功能梯度圆柱壳中纵向导波的截止频率ωnW/MHzTable 8 The cut-off frequencies ωnW/MHz of longitudinal waves in FGPPM cylinder shell with different gradient coefficient

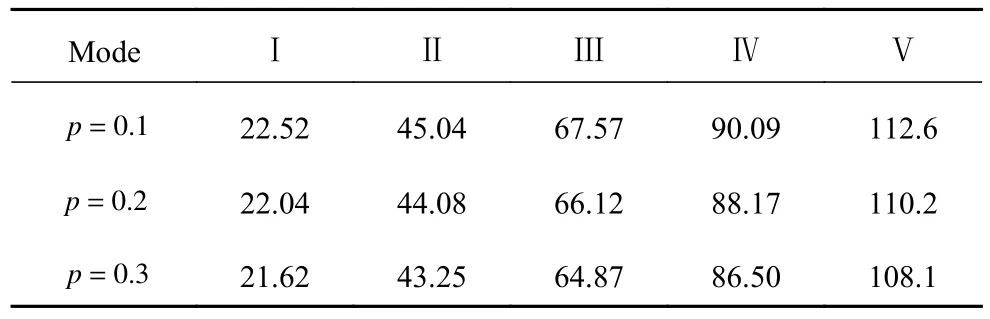
表9 不同梯度参数功能梯度圆柱壳中纵向导波的截止频率ωnU/MHzTable 9 The cut-off frequencies ωnW/MHz of longitudinal waves in FGPPM cylinder shell with different gradient coefficient

在前面的讨论中,所有的材料参数都是同时变化的,为了讨论某一类材料参数的变化对纵向导波截止频率的影响,在计算过程中,每次只使一类材料参数梯度变化,其余参数均保持为均质,选用第1 种变化形式的功能梯度压电压磁材料,分别计算弹性模量参数、电学参数、磁学参数和密度参数梯度变化的情况.在计算过程中取壳体内径Ra=9 mm,外径Rb=10 mm,p=0.1.计算结果如图2 和图3 所示,从图中可以看出随着弹性模量参数、电学参数和磁学参数梯度参数的增加,纵向波的截止频率也随之增加,而且可以明显看出,弹性模量参数变化对截止频率的影响最大,磁学参数对截止频率的影响最小.而对于密度参数,梯度参数的增加会使截止频率减小.

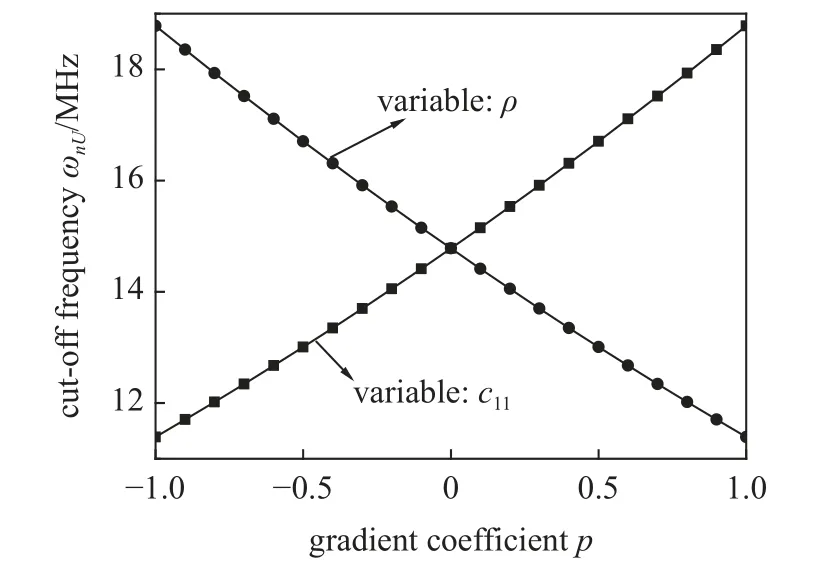
图2 材料参数梯度变化对截止频率 ωnU 的影响Fig.2 Influence of material parameter gradient change on the cut-off frequencies ωnU

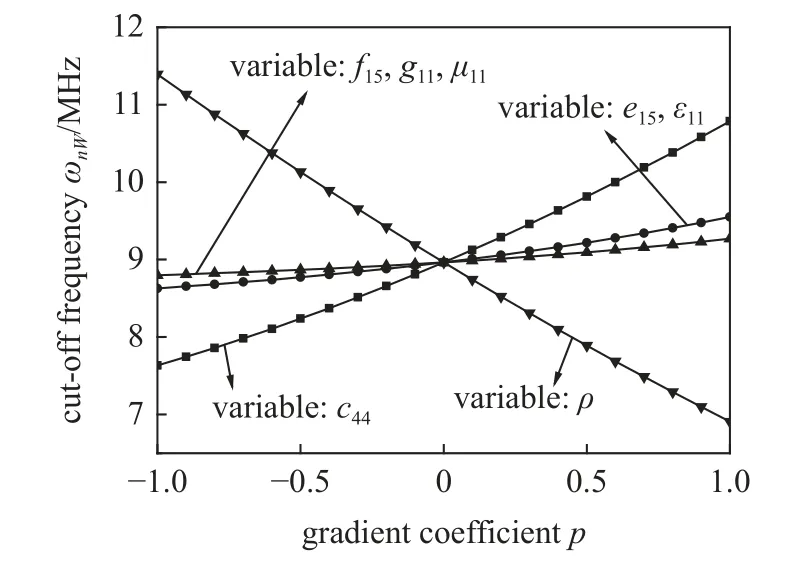
图3 材料参数梯度变化对截止频率 ωnW 的影响Fig.3 Influence of material parameter gradient change on the cut-off frequencies ωnW

3.3 壳体厚度对截止频率的影响

讨论了不同壳体厚度情况下纵向波的截止频率,在计算过程中选用算例中提出的第2 种材料.壳体内径保持不变,取Ra=9 mm,外径为1 0～12 mm,材料密度为常数,其余参数的梯度系数为p=0.1.计算结果如图4 所示.

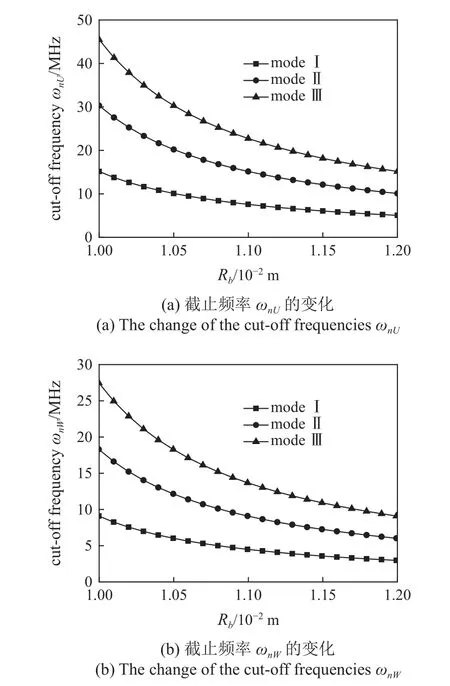
图4 圆柱壳厚度变化对截止频率的影响Fig.4 Influence of cylinder shell thickness change on the cut-off frequencies

从图4 中可以看出,在圆柱壳内径保持不变,厚度增加的情况下,纵向波各模态的截止频率会随着厚度的增大而减小,且高阶模态的减小趋势更为显著.

4 结论

本文用WKB 法研究了功能梯度压电压磁圆柱壳中纵向导波的截止频率.当材料退化为均质材料时,可以得到壳体纵向波截止频率的Bessel 函数解.分别对比均质压电压磁圆柱壳体中纵向导波的截止频率的Bessel 函数解和由功能梯度压电压磁圆柱壳体中纵向导波频散曲线所得的截止频率,验证了WKB 解的高精确性.通过数值算例可以发现,纵向导波的截止频率是两个近似等差数列集的集合;对于由 BaTiO3材料和 CoFe2O4材料复合而成的功能梯度压电压磁圆柱壳,纵向导波的截止频率介于BaTiO3圆柱壳和CoFe2O4圆柱壳的截止频率之间.对于功能梯度压电压磁圆柱壳中的纵向导波,弹性参数和密度梯度变化对截止频率影响较为明显;电学参数与磁学参数梯度变化对其截止频率影响较小;壳体厚度增加会导致截止频率降低.这些结论可为基于截止频率的非均质材料圆柱壳的超声无损检测提供理论依据.