面向属性概念格的概念约简及其在知识空间理论中的应用
于亚琪,赵思雨,魏 玲,3
(1.西北大学 数学学院,陕西 西安 710127;2.西北大学 概念、认知与智能研究中心,陕西 西安 710127;3.闽南师范大学 数学与统计学院,福建 漳州 363000)
1982年,Wille提出了形式概念分析(formal concept analysis, FCA)理论[1-2]。该理论对哲学中的“概念”进行形式化描述,并将所有概念按照一定的偏序关系和上下确界的定义,形成一个格结构,称之为概念格。经过多年的研究探索,形式概念分析在属性约简[3-5]、规则获取[6-8]、三支概念分析[9-10]等领域产生了一些研究成果。
Duntsch和Gediga在FCA框架下提出了面向属性概念格[11];Yao提出了面向对象概念格[12]。目前,关于面向属性概念格与面向对象概念格已产生了许多研究成果。比如:魏玲等提出了一种直接从形式背景出发,获得简化面向属性概念格的方法[13];Medina研究了概念格、面向属性概念格以及面向对象概念格的属性特征之间的关系[14];周银凤等基于面向属性概念格求解由合取技能映射确定的知识结构[15]。
近年来,为减少形式背景与概念格中存在许多冗余信息的问题,许多约简理论被相继提出。其中:魏玲等于2018年提出的保持二元关系不变的概念约简是形式概念分析中新的约简理论[16-17],与属性约简相比,既避免了原始信息发生改变,又减少了概念数量;王霞等利用概念可辨识矩阵给出了一种求解概念约简的方法[18];谢小贤等借助布尔矩阵运算研究了概念约简问题[19];Zhao等从代表概念矩阵角度给出了求解概念约简的方法[20];智慧来等把概念约简思想引入面向对象概念格,并研究了面向对象概念约简的相关问题[21]。
目前,关于概念约简的相关研究还没有涉及面向属性概念约简。本文研究面向属性概念格的概念约简及其在知识空间理论中的应用。
本文首先给出面向属性概念约简的定义,随后引入POC代表概念矩阵,基于POC代表概念矩阵给出面向属性概念约简的求解方法与面向属性概念特征;其次,结合面向对象概念约简,给出面向属性概念约简与面向对象概念约简之间的联系;最后,从知识空间的角度,探讨面向属性概念约简的意义。
1 预备知识
定义1[1]称(G,M,I)是形式背景,其中G={g1,…,gp}为对象集,M={m1,…,mq}为属性集,I⊆G×M为G和M之间的二元关系。(g,m)∈I,表示对象g具有属性m,记为gIm。(g,m)∉I,表示对象g不具有属性m,记为gIcm。
对任意的X⊆G,B⊆M,Wille[1]定义了一对导出算子如下,其性质见文献[2]。
X*={m∈M|∀g∈X,gIm},
(1)
B*={g∈G|∀m∈B,gIm}。
(2)
式中:X*表示X中的所有对象共同具有的属性集合;B*表示共同具有B中所有属性的对象集合。如果二元组(X,B)满足X*=B且X=B*,则称(X,B)是一个概念。其中X称为概念的外延,B称为概念的内涵。
类似地,对任意的X⊆G,B⊆M,Qi[9]定义了一对负算子如下,其性质见文献[9]。
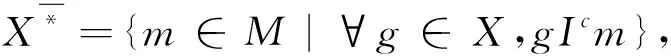
(3)
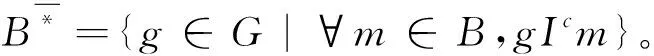
(4)
Duntsch和Gediga[11]在对象集和属性集上分别定义了□、◇,并给出了面向属性概念的定义。
定义2[11]设(G,M,I)是形式背景,在对象集X⊆G和属性集B⊆M上,定义一对近似算子□、◇。
X□={m∈M|m*⊆X};
(5)
X◇={m∈M|m*∩X≠∅};
(6)
B□={g∈G|g*⊆B};
(7)
B◇={g∈G|g*∩B≠∅}。
(8)
对于□、◇,有以下基本性质。
性质1[11-12]设(G,M,I)形式背景,X1,X2,X⊆G,B1,B2,B⊆M,有下列基本性质:
2)X□◇□=X□,X◇□◇=X◇;
B□◇□=B□,B◇□◇=B◇。
定义3[11]如果二元组(X,B)满足X=B□且B=X◇,则称(X,B)为面向属性概念。其中X称为面向属性概念的外延,B称为面向属性概念的内涵。
将形式背景(G,M,I)上的面向属性概念全体记为Lp(G,M,I)。
若(X1,B1)和(X2,B2)是面向属性概念,其偏序关系定义为(X1,B1)≤(X2,B2)⟺X1⊆X2(⟺B1⊆B2),则(Lp(G,M,I),≤)是偏序集。上确界和下确界分别为
(X1,B1)∨(X2,B2)=((X1∪X2)◇□,B1∪B2),
(X1,B1)∧(X2,B2)=(X1∩X2,(B1∩B2)□◇),
则(Lp(G,M,I),∨,∧)是完备格,称之为面向属性概念格。
面向对象概念格的相关定义及性质见文献[12]。
例1表1给出了一个形式背景(G,M,I) 。其中:对象集G={1,2,3,4,5} ;属性集M={a,b,c,d,e,f,g}。(g,m)∈I用1表示,(g,m)I用0表示。该形式背景的面向属性概念格如图1所示。为了方便表述,将每个面向属性概念以ci(i=1,2,…,9)编号。
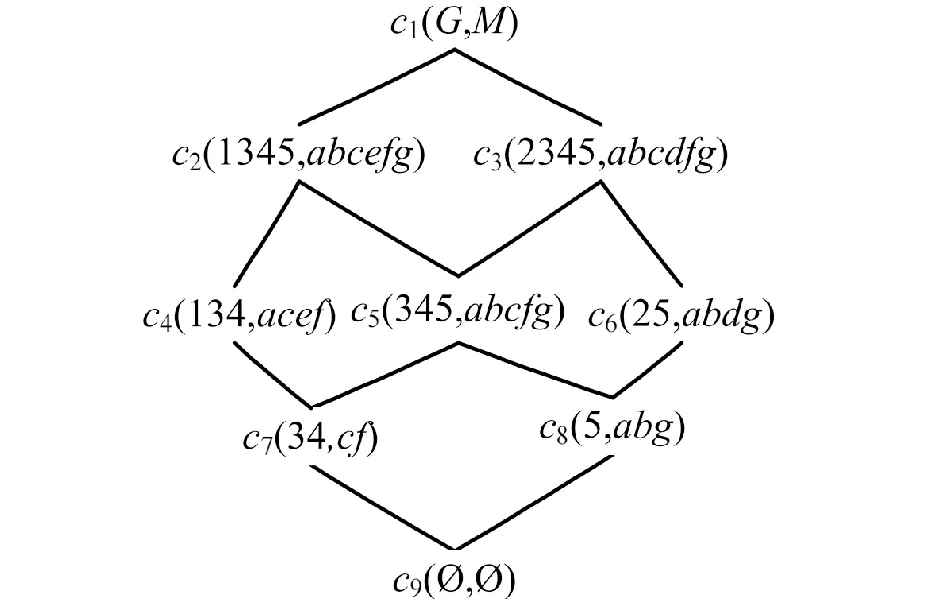
图1 面向属性概念格Lp(G,M,I)Fig. 1 Property-oriented concept lattice Lp(G,M,I)
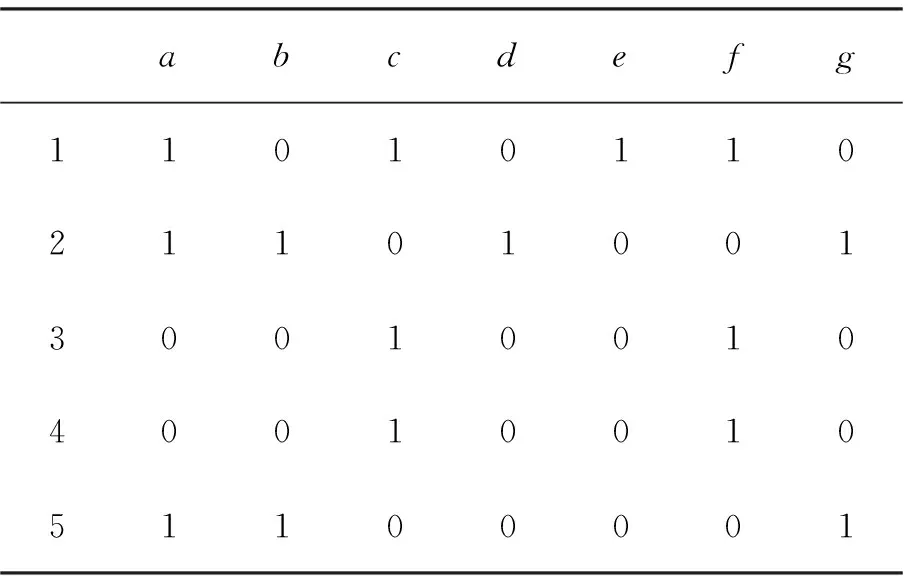
表1 形式背景(G,M,I) Tab. 1 Formal context (G,M,I)
2 面向属性概念约简
2.1 面向属性概念约简的定义及存在性
本小节从保持形式背景补二元关系不变的角度给出面向属性概念约简的定义,并给出两种特殊的面向属性概念协调集。
文献[2]给出了形式背景的二元关系与其所有概念之间的关系,如下引理所示。
引理1[2]设(G,M,I)是形式背景,L(G,M,I)是其概念格,有
I=∪{X×B|(X,B)∈L(G,M,I)}。
类似地,补二元关系可表示为
Ic=∪{X×B|(X,B)∈NL(G,M,I)}。
根据算子之间的联系,面向属性概念与N概念的关系如下。
性质2[14]设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格,NL(G,M,I)是其N概念格,有
(X,B)∈Lp(G,M,I)⟺(X,Bc)∈NL(G,M,I)。
由引理1和性质2易得补二元关系也可由所有面向属性概念生成。
定理1设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格,则
Ic=∪{X×Bc|(X,B)∈Lp(G,M,I)}。
定义4设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格,F⊆Lp(G,M,I)。如果Ic=∪(X,B)∈FX×Bc,则称F为保持补二元关系不变的面向属性概念格的概念协调集,简称面向属性概念协调集;若对于任意(X0,B0)∈F,F′=F{(X0,B0)},有Ic≠∪(X,B)∈F′X×Bc,则称F为保持补二元关系不变的面向属性概念格的概念约简,简称面向属性概念约简。
定理2设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格,则面向属性概念约简必存在。
证明若对任意(X0,B0)∈Lp(G,M,I),有∪(X,B)∈Lp(G,M,I)X×Bc≠∪(X,B)∈Lp(G,M,I){(X0,B0)}X×Bc,则Lp(G,M,I)本身即为面向属性概念约简。若存在(X1,B1)∈Lp(G,M,I),使∪(X,B)∈Lp(G,M,I)X×Bc=∪(X,B)∈Lp(G,M,I){(X1,B1)}X×Bc,则研究F=Lp(G,M,I){(X1,B1)},若对于任意(X2,B2)∈F,有∪(X,B)∈FX×Bc≠∪(X,B)∈F{(X2,B2)}X×Bc,则F为面向属性概念约简,否则,进一步研究F1=F{(X2,B2)},重复上述过程,由于Lp(G,M,I)是有限集,所以,至少可以找到一个约简。因此,面向属性概念约简必存在。
性质3对于任意g∈G,m∈M,一定有
(g◇□,g◇)∈Lp(G,M,I),
(m◇c,m◇c◇)∈Lp(G,M,I)。
证明由定义2可得,m◇c={g∈G|gIcm}=mc□,则m◇c◇=mc□◇,故(m◇c,m◇c◇)=(mc□,mc□◇)。由定义3和性质1可知,(g◇□,g◇)∈Lp(G,M,I),(m◇c,m◇c◇)∈Lp(G,M,I)。
定义5设(G,M,I)是形式背景,称(g◇□,g◇)是面向属性概念格的对象概念。记所有面向属性概念格的对象概念的集合为Op(G,M,I)。对偶地,称(m◇c,m◇c◇)是面向属性概念格的属性概念。记所有面向属性概念格的属性概念的集合为Ap(G,M,I)。
本文中面向属性概念格的对象概念与属性概念分别简称为对象概念与属性概念。
定理3Op(G,M,I)与Ap(G,M,I)均为面向属性概念协调集。
例2(续例1)由例1可知在形式背景(G,M,I)中,1◇={a,c,e,f},1◇□={1,3,4},a◇c={3,4},a◇c◇={c,f},由定义5知,c4为对象概念,c7为属性概念。类似地,得Op(G,M,I)={c4,c6,c7,c8},Ap(G,M,I)={c2,c3,c4,c6,c7}。可验证此时Op(G,M,I)、Ap(G,M,I)均是面向属性概念协调集。
2.2 面向属性概念约简求解方法
本小节给出面向属性概念协调集判定定理,并从POC代表概念矩阵的角度给出面向属性概念约简的求解方法。
定义6设(G,M,I)是形式背景,g∈G,m∈M,(X,B)∈LP(G,M,I)。如果(g,m)∈X×Bc,则称(X,B)是(g,m)关于面向属性概念的代表概念,简称POC代表概念,其全体记为REP((g,m))。在此基础上,称
Λ={REP((g,m))|(g,m)∈X×Bc}
(9)
为形式背景(G,M,I)关于面向属性概念的代表概念矩阵,简称POC代表概念矩阵。
事实上,与所有非空REP((g,m))相交非空的面向属性概念集就是面向属性概念协调集。
定理4(面向属性概念协调集判定定理) 设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格。对于任意F⊆Lp(G,M,I),F≠∅,下列命题等价:
1)F是面向属性概念协调集;
2) 对于任意(g,m)∈Ic,F∩REP((g,m))≠∅;
3) 对于任意D⊆Lp(G,M,I),若F∩D=∅,则D∉Λ。
证明1)⟹2)。由F是面向属性概念协调集可知:Ic=∪(X,B)∈FX×Bc。 所以对任意(g,m)∈Ic,存在(X,B)∈F,使得(g,m)∈X×Bc,即(X,B)∈REP((g,m))。故F∩REP((g,m))≠∅。
2)⟹1)。对任意(g,m)∈Ic,F∩REP((g,m))≠∅,故存在(X,B)∈F,满足(X,B)∈REP((g,m)),即存在(X,B)∈F满足(g,m)∈X×Bc。因此,∪(X,B)∈FX×Bc=∪(g,m)∈X×Bc,(X,B)∈F{(g,m)}=Ic,故F是面向属性概念协调集。
2)⟹3)。假设D∈Λ,因为Λ={REP((g,m))|(g,m)∈X×Bc}且对于任意(g,m)∈Ic,F∩REP((g,m))≠∅,所以F∩D≠∅,矛盾。因此,D∉Λ。
3)⟹2)。假设对于任意的(g,m)∈Ic,有F∩REP((g,m))=∅。因为对于任意D⊆Lp(G,M,I),若F∩D=∅,有D∉Λ,所以REP((g,m))∉Λ,矛盾。故对于任意(g,m)∈Ic,F∩REP((g,m))≠∅。
结合定义4与定理4即可得到面向属性概念约简判定定理。
定理5(面向属性概念约简判定定理) 设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格。对于任意F⊆Lp(G,M,I),若满足以下两个条件:
1)对于任意(g,m)∈Ic,F∩REP((g,m))≠∅;
2)对于任意(X,B)∈F,有(g0,m0)∈Ic,使得(F{(X,B)})∩REP((g0,m0))=∅。
则F是面向属性概念约简。
在POC代表概念矩阵中存在一些冗余的REP((g,m)),使得求解面向属性概念约简的时间复杂度有所增加。为解决此问题,定义了最小POC代表概念矩阵Λmin。
定义7设(G,M,I)是形式背景,Λmin是包含关系下由所有极小REP((g,m))组成的矩阵,则称Λmin为形式背景(G,M,I)的最小POC代表概念矩阵。
基于最小POC代表概念矩阵给出求解面向属性概念约简的方法。
定义8设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格,面向属性概念的代表概念函数定义为
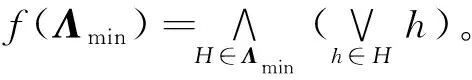
(10)
f(Λmin)所对应的最小析取范式的所有合取式为形式背景(G,M,I)的所有面向属性概念约简。
例3(续例1) 由性质2可知所有补概念为(G,∅),(1345,d),(2345,e),(134,bdg),(345,de),(25,cef),(34,abdeg),(5,cdef),(∅,M)。遍历所有补概念可知,(1,b)∈{1,3,4}×{b,d,g},所以,由定义6知REP((1,b))={({1,3,4},{a,c,e,f})}={c4}。类似地,对于任意g∈G,m∈M,REP((g,m))即可得。由此,形式背景(G,M,I)的POC代表概念矩阵与最小POC代表概念矩阵为
进而得
f(Λmin)=
c4∧c6∧c7∧(c2∨c5∨c8)=
(c2∧c4∧c6∧c7)∨(c4∧c5∧
c6∧c7)∨(c4∧c6∧c7∧c8)。
即形式背景的面向属性概念约简有3个,分别是
F1={c2,c4,c6,c7},
F2={c4,c5,c6,c7},
F3={c4,c6,c7,c8}。
2.3 面向属性概念特征
每个面向属性概念在面向属性概念格中所起的作用是不同的,本小节从面向属性概念约简出发,将面向属性概念分为3类,即核心面向属性概念,相对必要面向属性概念,绝对不必要面向属性概念,并分别研究其特征。
定义9设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格。记R={Fi|i∈τ,τ为指标集}为(G,M,I)的所有面向属性概念约简的集合,则Lp(G,M,I)可分为3类:
1)核心面向属性概念集C=∩i∈τFi;
2)相对必要面向属性概念集
K=∪i∈τFi∩i∈τFi;
3)绝对不必要面向属性概念集
U=Lp(G,M,I)∪i∈τFi。
例4(续例1) 在形式背景(G,M,I)中,C={c4,c6,c7},K={c2,c5,c8},U={c1,c3,c9}。
下面从POC代表概念矩阵角度给出核心面向属性概念的概念特征。
定理6设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格。c∈C当且仅当存在(g,m)∈Ic,使得REP((g,m))={c}。
证明c∈C⟺Lp(G,M,I){c}不是面向属性概念协调集⟺存在(g,m)∈Ic,使得Lp(G,M,I){c}∩REP((g,m))=∅⟺存在(g,m)∈Ic使得REP((g,m))={c}。
定理7从最小POC代表概念矩阵角度给出绝对不必要面向属性概念的概念特征。
定理7设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格。c∈U当且仅当对于任意REP((g,m))∈Λmin,c∉REP((g,m))。
证明必要性。假设存在REP((g,m))∈Λmin,c∈REP((g,m)),由定理4可知,存在面向属性概念约简F0,使得c∈F0,即c∉U,矛盾。故对任意REP((g,m))∈Λmin,c∉REP((g,m))。
充分性。假设c∉U,则存在面向属性概念约简F0,使得c∈F0。即存在REP((g,m))∈Λmin,使得c∈REP((g,m)),矛盾。故c∈U。
结合定理6与定理7,可得相对必要面向属性概念特征如推论1。
推论1设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格。c∈K当且仅当存在REP((g,m))∈Λmin,c∈REP((g,m))且对于任意(g,m)∈Ic,满足REP((g,m))≠{c}。
3 面向属性概念约简与面向对象概念约简的关系
智慧来等在文献[21]中研究了面向对象概念约简,本文第2节中主要研究了面向属性概念约简,本节讨论两者之间的关系。
定义10[21]设(G,M,I)是形式背景,Lo(G,M,I)是其面向对象概念格,F⊆Lo(G,M,I)。如果Ic=∪(X,B)∈FXc×B,则称F为面向对象概念协调集;若对于任意(X0,B0)∈F,F′=F{(X0,B0)},有Ic≠∪(X,B)∈F′Xc×B,则称F为面向对象概念约简。
引理2给出面向属性概念与面向对象概念之间的关系。
引理2[14]设(G,M,I)是形式背景,Lp(G,M,I)是其面向属性概念格,Lo(G,M,I)是其面向对象概念格。(X,B)∈Lp(G,M,I)当且仅当(Xc,Bc)∈Lo(G,M,I)。
下面从定义角度给出面向属性概念约简与面向对象概念约简之间的联系。
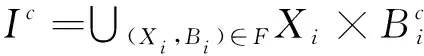
充分性同理可证。
由定理8可知,面向属性概念约简与面向对象概念约简可相互得到。下面定理说明面向属性概念特征与面向对象概念特征之间的关系。
定理9设(G,M,I)是形式背景,Lp(G,M,I)与Lo(G,M,I)分别是其面向属性概念格与面向对象概念格。C、K、U分别是核心、相对必要、绝对不必要面向属性概念集,Co、Ko、Uo分别是核心、相对必要、绝对不必要面向对象概念集。对于任意(X,B)∈Lp(G,M,I),有
1) (X,B)∈C⟺(Xc,Bc)∈Co;
2) (X,B)∈K⟺(Xc,Bc)∈Ko;
3) (X,B)∈U⟺(Xc,Bc)∈Uo。
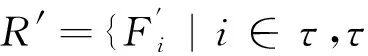
2)、3)同理可得。
例5(续例1) 由定理8知,形式背景(G,M,I)的面向对象概念约简分别为
由定理9可知,核心面向对象概念集Co、相对必要面向对象概念集Ko、绝对不必要面向对象概念集Uo分别为
Co={(25,bdg),(134,cef),(125,abdeg)},
Ko={(2,d),(12,de),(1234,cdef)},
Uo={(∅,∅),(1,e),(G,M)}。
4 面向属性概念约简的应用
Rusch和Wille在文献[22]中将知识空间与形式背景相结合,提出了由形式背景构造知识空间的方法。李进金等通过知识基建立了形式背景和知识空间的联系[23]。周银凤等将合取技能映射转换成技能背景,通过求解技能背景的所有面向属性概念得到由合取技能映射诱导的知识结构[15]。对于合取技能映射诱导的知识结构,可通过所有面向属性概念确定相应的技能背景。但由合取技能映射诱导的知识结构中存在冗余信息,本节通过面向属性概念约简对应的部分知识结构确定与之对应的技能背景。
首先,给出知识结构的定义。
定义11[24]给定问题集Q,学习者能解决的问题子集K⊆Q称为知识状态。(Q,K )为知识结构,其中,K 是由知识状态构成的集族且至少包含∅和Q。
在问题集Q明确的情况下,知识结构简记为K 。
例6假设问题集为Q={1,2,3,4,5},则K1=P (Q),K2={∅,{1,2},Q}都是知识结构。
定义12[25]三元组(Q,S,μ)称为一个合取技能映射。其中:Q为非空问题集;S为非空技能集;μ为Q到2S∅的映射,且对于任意q∈Q,μ(q)⊆S表示解决问题q的极小能力。对任意技能子集T⊆S,T通过合取技能映射μ诱导的知识状态表示为K={q∈Q|μ(q)⊆T}。所有的知识状态组成的知识结构用K 表示。
下面,给出合取技能映射与技能背景之间的联系。
定义13[15]设(Q,S,μ)是合取技能映射,问题集Q为对象,技能集S为属性,根据关系s∈μ(q)⟺(q,s)∈I,则合取技能映射(Q,S,μ)可转换为形式背景(Q,S,I),称这样的形式背景为技能背景。
例7给定合取技能函数(Q,S,μ)。其中:Q={1,2,3,4,5}表示5个问题;S={a,b,c,d,e,f,g}表示7种办公技能,a表示文案撰写,b表示LaTeX排版,c表示Word排版,d表示外文翻译,e表示Python编程,f表示宣传策划,g表示图片处理。设μ(1)={a,c,e,f},μ(2)={a,b,d,g},μ(3)={c,f},μ(4)={c,f},μ(5)={a,b,g},则技能背景(Q,S,I)如表2所示。其中,μ(5)={a,b,g}表示求解问题5需至少具备技能a,b,g。

表2 技能背景(Q,S,I)Tab. 2 Skill context(Q,S,I)
定理10[15]设(Q,S,I)是与合取技能映射(Q,S,μ)对应的技能背景。对于任意(K,T)∈Lp(Q,S,I),技能子集T⊆S通过μ诱导的知识状态为K,记
K ={K|(K,T)∈Lp(Q,S,I)},
则K 是由μ诱导得到的知识结构。
由于知识结构是所有面向属性概念的外延组成的集族,根据本文第2节可知所有面向属性概念可确定技能背景中的所有补二元关系,即由知识结构可确定与之对应的技能背景。但知识结构中存在冗余信息,通过面向属性概念约简的定义可知,面向属性概念约简即可确定形式背景中所有补二元关系,即由面向属性概念约简的外延构成的部分知识结构可确定与之对应的技能背景。
例8(续例7)技能背景中的所有面向属性概念为c1=(Q,S),c2=(1345,abcefg),c3=(2345,abcdfg),c4=(134,acef),c5=(345,abcfg),c6=(25,abdg),c7=(34,cf),c8=(5,abg),c9=(∅, ∅)。 其中,c6=(25,abdg)表示解决问题2与问题5需至少具备技能a,b,d,g。
由定理9可知,合取技能映射诱导的知识结构为K ={Q,{1,3,4,5},{2,3,4,5},{1,3,4},{3,4,5},{2,5},{3,4},{5},∅}。由知识结构K 可得对应的技能背景,即表2。
由例3可知,技能背景(Q,S,I)有3个面向属性概念约简,分别为F1={c2,c4,c6,c7},F2={c4,c5,c6,c7},F3={c4,c6,c7,c8}。以F1为例,{c2,c4,c6,c7}包含的部分知识结构是K ′={{1,3,4,5},{1,3,4},{2,5},{3,4}},通过K ′即可确定与之对应技能背景(Q,S,I)。
5 结语
概念约简作为一种新的约简理论,既保持了形式背景原始信息不变,又减少了概念数量。本文将概念约简思想引入面向属性概念格,研究了面向属性概念约简的问题。 首先,给出了面向属性概念约简的定义,随后给出了面向属性概念约简的求解方法并根据面向属性概念在约简中的不同作用,将其分为核心、相对必要、绝对不必要面向属性概念;其次,从定义角度探讨了面向属性概念约简与面向对象概念约简之间的关系;最后,给出了面向属性概念约简在知识空间中的应用。
形式概念分析的研究已不再局限于经典的形式背景,因此,如何将面向属性概念约简理论扩展到不完备形式背景、模糊背景、区间值背景也是值得探讨的问题。

