对称形式背景及其概念约简
魏 玲,赵思雨,2,祁建军
(1.西北大学 数学学院,陕西 西安 710127; 2.咸阳师范学院 数学与统计学院,陕西 咸阳 712000;3.新疆政法学院 信息网络安全学院,新疆 图木舒克 844000;4.西安电子科技大学 计算机科学与技术学院,陕西 西安 710071)
形式概念分析(formal concept analysis, FCA)是以形式背景为数据基础的知识发现理论,于1982年由德国数学家Wille提出[1]。
FCA的研究主题包括概念格构造[2-3],概念格简化[4]、约简[5-17]、规则获取[18-19]、应用[19]等。其中,约简理论主要包括属性约简[5-10]及概念约简[11-17]。属性约简的目标是以极小的属性子集保持某一特性不变,如张文修[5]、魏玲[6]等研究保持概念格结构不变的属性约简,此外还有保持粒[7],交、并不可约元[8-9],决策规则不变[10]的属性约简。概念约简作为一个新的约简理论,其研究目标主要集中于以极小的概念子集保持形式背景的关系不变。魏玲[11]、曹丽[12]等提出了保持二元关系不变的概念约简(简称概念约简),给出了概念约简的计算方法,并将概念分类,研究了每类概念的概念特征。随后,谢小贤等通过布尔矩阵运算研究了概念特征和概念约简[13];王霞等定义了概念可辨识矩阵,并基于此矩阵给出概念约简求解方法[14];马文胜等提出了同效关系,并给出由同效关系子集补集的概念格来得到概念约简的新算法[15];Zhao等定义了代表概念矩阵,并给出了一种直观的寻找概念约简的方法[16];李俊余等提出了三元背景中保留所有三元关系的三元概念约简[17]。
形式背景是FCA的研究起点,关于形式背景变化的研究是FCA的研究热点。决策形式背景在形式背景的基础上加入了决策属性,魏玲等针对决策形式背景定义了背景的协调性并讨论了属性约简[6],随后研究了决策形式背景的规则提取[18]。由于不确定数据的广泛存在性和不可避免性,许多学者也探索了不完备背景[20],模糊背景[21],区间值背景[22]等不确定性背景的理论研究及实际应用。此外,FCA与冲突分析、社交网络等领域结合,可用于解决各自领域的基本问题,而连接不同领域的基石与桥梁恰为形式背景。王艺超等在冲突分析中利用代理人之间的复合冲突程度定义了联盟形式背景,并利用联盟形式背景获取了极大联盟[23];Hao等将社交网络转化为基于修正邻接矩阵的形式背景,并利用该形式背景上的k-等势概念探测了社交网络中的k-团[24]。
通过观察发现,联盟形式背景及基于修正邻接矩阵的形式背景可一般化为一类特殊的形式背景,本文称其为对称形式背景。事实上,在任何团体中,若团体内部关系具有自反性和对称性的特点,则该关系可以表示于对称形式背景中。因此,对称形式背景在FCA中占据着重要的地位,有必要对对称形式背景及其性质展开研究。另外,作为特殊的形式背景,对称形式背景的概念约简也具有特殊性,因此,本文亦探讨了对称形式背景的概念约简。
本文首先定义了对称形式背景并讨论了其性质;其次,研究了对称形式背景上由对称概念构成的概念约简;最后,给出了对称形式背景及其概念格在冲突分析、社交网络等领域的实际应用。
1 FCA基础知识
定义1[1]称三元组(G,M,I)为形式背景。其中:G={x1,x2,…,xn}为对象集,xi(i≤n)称为对象;M={a1,a2,…,am}为属性集,aj(j≤m)称为属性;I⊆G×M为G与M之间的二元关系。对于任意的x∈G及a∈M,若(x,a)∈I,称对象x具有属性a或属性a被对象x具有,记为xIa;若(x,a)∉I,称对象x不具有属性a或属性a不被对象x具有,记为xIca。
对于任意的对象子集X⊆G,属性子集A⊆M,引入记号
XIA⟺∀x∈X,a∈A,s.t.xIa;
XIcA⟺∃x∈X,a∈A,s.t.xIca。
设(G,M,I)为形式背景,在对象子集X⊆G和属性子集A⊆M上定义一对对偶算子
X*={a∈M|∀x∈X,xIa},
A*={x∈G|∀a∈A,xIa}。
对偶算子的相关性质见文献[1]。特别地,对于任意的对象x∈G,属性a∈M,记{x}*为x*,{a}*为a*。
定义2[1]设(G,M,I)为形式背景,X⊆G,A⊆M。如果一个二元对(X,A)满足X*=A且A*=X,则称(X,A)是一个形式概念,简称概念。其中:X为概念的外延;A为概念的内涵。
在形式背景中,对任意的对象x∈G,属性a∈M,(x**,x*)和(a*,a**)也是概念,分别被称为对象概念及属性概念。
用L(G,M,I)表示形式背景(G,M,I)的全体概念,对于任意的(X1,A1),(X2,A2)∈L(G,M,I),定义偏序关系
(X1,A1)≤(X2,A2)⟺X1⊆X2(⟺A2⊆A1)则L(G,M,I)形成一个完备格,称为概念格。其中上、下确界为
(X1,A1)∨(X2,A2)=((X1∪X2)**,A1∩A2),
(X1,A1)∧(X2,A2)=(X1∩X2,(A1∪A2)**)。
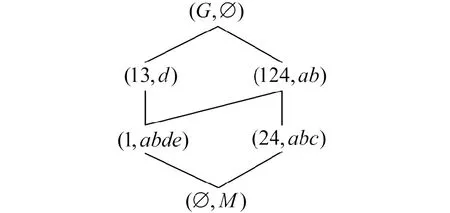
设L为格,x∈L,若x≠∨{l∈L|l 本文记概念格L(G,M,I)中对象概念的全体为O(L),属性概念的全体为A(L),并不可约概念的全体为J(L),交不可约概念的全体为M(L)。 例1表1是一个形式背景(G,M,I)。其中:对象集G={1,2,3,4};属性集M={a,b,c,d,e}。如果对象具有属性,则在对象行与属性列的交叉处用1标记,否则用0标记。 表1 形式背景(G,M,I)Tab.1 A formal context (G,M,I) 形式背景(G,M,I)对应的概念格L(G,M,I)如图1所示,4种概念集合分别为 图1 概念格L(G,M,I)Fig.1 A concept lattice L(G,M,I) O(L)={(1,abde),(24,abc),(13,d)}, A(L)={(124,ab),(24,abc),(13,d), (1,abde)}, J(L)={(1,abde),(24,abc),(13,d)}, M(L)={(124,ab),(24,abc),(13,d)}。 王艺超等[23]和Hao等[24]分别将FCA与冲突分析、社交网络相结合,研究了相关领域的基本问题。由于连接这些不同理论的桥梁是一类特殊的形式背景,称其为对称形式背景,并研究其性质。 定义3设(G,M,I)为形式背景。其中:G={x1,x2,…,xn};M={a1,a2,…,am}。若n=m且对于任意的xi,xj∈G,ai,aj∈M,1≤i,j≤n,满足i=j时,xiIaj;i≠j时,xiIaj⟺xjIai,则称(G,M,I)为对称形式背景。 事实上,对称形式背景可以看作是一个对称矩阵。不失一般性,本文在后续研究中把对称形式背景的对象集和属性集看作相同的集合,并记对称形式背景为(G,G,I),其中G={x1,x2,…,xn}。 例2表2是一个对称形式背景(G,G,I)。其中,G={1,2,3,4,5,6}。图2为相应的概念格L(G,G,I)。其中: 图2 对称形式背景(G,G,I)的概念格L(G,G,I)Fig.2 The concept lattice L(G,G,I) of a symmetric formal context (G,G,I) 表2 对称形式背景(G,G,I)Tab.2 A symmetric formal context (G,G,I) O(L)=J(L)={(16,1246),(2,1256),(346,346),(46,1346),(25,25),(6,12346)}; A(L)=M(L)={(1246,16),(1256,2),(346,346),(1346,46),(25,25),(12346,6)}。 下面探讨对称形式背景的概念格的特征。 定理1设(G,G,I)为对称形式背景,L(G,G,I)为其概念格,对于任意的(X,Y)∈L(G,G,I),都有(Y,X)∈L(G,G,I)。 证明对于任意的(X,Y)∈L(G,G,I),有Y=X*,X=Y*,Y⊆G,X⊆G,故(Y,X)∈L(G,G,I)。 定理1表明对称形式背景的概念格中任意一个概念都存在与其自身外延和内涵互换的概念。 本文将对称形式背景(G,G,I)的概念格L(G,G,I)称为对称概念格。图2就是对称概念格的一个例子。 下面探究对称形式背景的对象概念、属性概念、并不可约概念、交不可约概念等概念的特征。 定理2设(G,G,I)为对称形式背景,L(G,G,I)为其概念格,则(X,Y)∈O(L)⟺(Y,X)∈A(L)。 定理2表明对称形式背景中对象概念和属性概念一一对应,并且有对应关系的对象概念和属性概念的外延和内涵互换。 定理3设(G,G,I)为对称形式背景,L(G,G,I)为其概念格,则(X,Y)∈J(L)⟺(Y,X)∈M(L)。 证明必要性。设(X,Y)∈J(L),即(X,Y)≠(H,M),其中(H,M)=∨{(P,Q)∈L(G,G,I)|(P,Q)<(X,Y)}。因为(H,M)≤(X,Y),所以(X,Y)≤/(H,M),即XH且MY。对于任意的(P,Q)∈{(P,Q)∈L(G,G,I)|(P,Q)<(X,Y)},P⊂X,Y⊂Q且由定理1知(Y,X),(Q,P)∈L(G,G,I),故(Y,X)<(Q,P),则∧{(Q,P)∈L(G,G,I)|(Y,X)<(Q,P)}=(M,H)。由于(M,H)≤/(Y,X),所以(Y,X)≠(M,H),故(Y,X)∈M(L)。充分性类似可证。 定理3表明对称形式背景中并不可约概念和交不可约概念一一对应,并且有对应关系的并不可约概念和交不可约概念的外延和内涵互换。 定理4设(G,G,I)为对称形式背景,L(G,G,I)为其概念格。下列结论成立: 1) 若(X,Y)∈O(L),则X⊆Y; 2) 若(X,Y)∈A(L),则Y⊆X。 定理4表明对称形式背景中对象概念的外延包含于内涵,属性概念的内涵包含于外延。又由J(L)⊆O(L),M(L)⊆A(L)[1],易得如下推论。 推论1设(G,G,I)为对称形式背景,L(G,G,I)为其概念格。下列结论成立: 1) 若(X,Y)∈J(L),则X⊆Y; 2) 若(X,Y)∈M(L),则Y⊆X。 推论1表明对称形式背景中并不可约概念的外延包含于内涵,交不可约概念的内涵包含于外延。 显然,若一个概念同时是对象概念和属性概念,或同时是并不可约概念和交不可约概念,则其外延一定等于内涵,相关结论见推论2。 推论2设(G,G,I)为对称形式背景,L(G,G,I)为其概念格。下列结论成立: 1) 若(X,Y)∈O(L)∩A(L),则X=Y; 2) 若(X,Y)∈J(L)∩M(L),则X=Y。 注:定理4、推论1及推论2的逆命题不成立,可由例2中(126,126)∈L(G,G,I)验证。 外延和内涵相等的概念在对称形式背景的相关知识发现中有重要作用。本文将此类概念定义为对称概念,并在后文中研究由对称概念构造的概念约简及其相关性质。 定义4设(G,G,I)为对称形式背景,L(G,G,I)为其概念格,(X,Y)∈L(G,G,I)。若X=Y,称(X,Y)为对称概念。 记对称概念集为SC,即SC={(X,Y)∈L(G,G,I)|X=Y}。 例3(续例2)对称概念格L(G,G,I)的对称概念集SC={(25,25),(126,126),(146,146),(346,346)}。 魏玲[11]、曹丽[12]等提出的概念约简指保持形式背景二元关系不变的极小概念集。对称概念作为对称形式背景中的特殊概念,与概念约简有密切的联系。本节研究对称形式背景上由对称概念构造的概念约简及其相关性质。 对称形式背景是特殊的形式背景,利用代表概念矩阵[16]可以求解对称形式背景的所有概念约简。而其中存在一类特殊的概念约简,即对称概念集SC。下面对以上事实展开证明,即对称概念集是对称形式背景的一个概念约简。 首先,任意对称形式背景中一定存在对称概念。 定理5设(G,G,I)为对称形式背景,L(G,G,I)为其概念格。SC={(X,Y)∈L(G,G,I)|X=Y},则SC≠∅。 证明对于任意的xi∈G,由背景对称知xiIxi。考虑{xi},若对于任意的xj∈G(i≠j)满足xiIcxj,由背景对称知xjIcxi,故({xi},{xi})∈L(G,G,I);若存在xj∈G(i≠j)满足xiIxj,由背景对称知xjIxi,xiIxi,xjIxj,即{xi,xj}I{xi,xj},则考虑{xi,xj}。重复以上过程,由G是有限集知一定存在(X,X)∈L(G,G,I),即SC≠∅。 其次,定理6证明了对称概念集是一个概念约简。 定理6设(G,G,I)为对称形式背景,L(G,G,I)为其概念格。SC={(X,Y)∈L(G,G,I)|X=Y},则SC是一个概念约简。 例4(续例2)对称形式背景(G,G,I)有10个概念约简,其中对称概念集SC={(25,25),(126,126),(146,146),(346,346)}就是一个概念约简。 作为对称形式背景中的概念约简,对称概念集SC具有独特的性质。在讨论其性质之前,先给出对称概念格的对称轴的定义。 定义6设L(G,G,I)为对称概念格,(X,Y)∈L(G,G,I)。若X⊄Y且Y⊄X,则称(X,Y)为轴概念。进一步,称AXIS(L)={(X,Y)∈L(G,G,I)|X⊄Y且Y⊄X}为对称概念格L(G,G,I)的对称轴。 由于对称概念的外延等于内涵,故对称概念一定是轴概念。 性质1设(G,G,I)为对称形式背景,L(G,G,I)为其概念格,则SC⊆AXIS(L)。 性质1给出了一种直观获取对称形式背景的一个概念约简的方法。即首先画出对称概念格;其次,确定对称概念格的对称轴;最后,在对称轴中找到所有的对称概念,对称概念的全体即为一个概念约简。需要注意的是,轴概念不一定为对称概念,如例5所示。 例5表3为对称形式背景(G,G,I)。其中,G={1,2,3,4}。图3为相应的对称概念格。显然,(12,34)是一个轴概念,但(12,34)不是对称概念。 图3 例5的对称概念格L(G,G,I)Fig.3 The symmetric concept lattice L(G,G,I) of example 5 表3 例5的对称形式背景(G,G,I) 对称概念是特殊的轴概念,满足以下性质。 性质2设(G,G,I)为对称形式背景,L(G,G,I)为其概念格,(Z,Z)∈SC。若(X,Y)∈L(G,G,I)满足(X,Y)≤(Z,Z),则存在(Y,X)∈L(G,G,I)使得(Z,Z)≤(Y,X);若(Z,Z)≤(X,Y),则(Y,X)≤(Z,Z)。 证明设(Z,Z)∈SC,对于任意的(X,Y)≤(Z,Z),(X,Y)∈L(G,G,I),有X⊆Z⊆Y,又由定理1知(Y,X)∈L(G,G,I),且由概念的偏序关系知(Z,Z)≤(Y,X);同理,对于任意的(Z,Z)≤(X,Y),有(Y,X)≤(Z,Z)。 下面给出核心概念集C和对称概念集SC之间的关系。 性质3设(G,G,I)为对称形式背景,L(G,G,I)为其概念格,则C⊆SC。 性质3显然成立。该性质表明对称形式背景中若存在核心概念,则一定是对称概念。即对称形式背景中若存在核心知识,则一定包含于SC。在此意义下,SC是一类重要的概念约简。 本节从冲突分析及社交网络的角度给出对称形式背景及对称概念格的实际应用。 冲突普遍存在于诉讼纠纷、政策制定、军事行动等方面。在冲突中,至少有两方(称为代理人)在某些议题上存在争议。而冲突分析[23, 25-28]是对冲突进行分析从而帮助决策者制定合理策略的理论。 Pawlak结合粗糙集理论首次提出了冲突分析的具体模型[25]。基于此,多位学者从不同角度或结合不同理论对冲突分析模型进行了改进或拓展[26-28]。其中,Yao结合三支决策理论给出了三支冲突分析模型[26]。三支冲突分析模型利用多值冲突表表示代理人关于议题的态度。 定义7[26]称三元组S=(A,I,r)为多值冲突表。其中:A={x1,x2,…,xn}为代理人集,A中每个元素xj(1≤j≤n)为一个代理人;I={i1,i2,…,im}为议题集,I中的每个元素ik(1≤k≤m)为一个议题;r:A×I→[-1,+1]为映射,r(xj,ik)表示代理人xj关于议题ik的态度的取值。 例6表4为多值冲突表S=(A,I,r)。其中:A={x1,x2,x3,x4,x5,x6};I={i1,i2,i3,i4,i5};r(xj,ik)为代理人xj关于议题ik的态度的取值,如r(x1,i3)=+0.9表示代理人x1支持议题i3的程度为0.9,r(x2,i4)=-0.5表示代理人x2反对议题i4的程度为0.5。 表4 多值冲突表(A,I,r)Tab.4 A many-valued conflict situation (A,I,r) 在冲突分析中,对代理人之间冲突程度的刻画是研究的焦点。Yao等利用距离函数定义了代理人之间的冲突程度[26],在此基础上,Lang等[28]和王艺超等[23]对其进行了改进。特别地,王艺超等[23]定义的复合冲突程度同时关注两个代理人关于议题态度取值的差别和每个代理人自身关于议题态度的取值,可以较为全面地刻画两个代理人之间的冲突程度。基于复合冲突程度,王艺超等研究了冲突场景中的极大联盟,即刻画了复合冲突程度小于等于给定阈值的极大的代理人集合,并借助形式概念分析定义了联盟形式背景,利用联盟形式背景中外延和内涵相等的等联盟概念获取了所有的极大联盟。 表2中对称形式背景为(G,G,I),其中G={1,2,3,4,5,6}。令6个对象(属性)表示6位代理人,给定议题子集,对于任意的xi,xj∈G,若代理人xi与代理人xj的复合冲突程度小于等于给定阈值,则用xiIxj表示代理人xi与代理人xj具有联盟关系,如取议题子集J={i2,i3},阈值(α,β)=(0.4,0.3),表4对应的联盟形式背景同表2。由此可得本文定义的对称形式背景直接对应冲突分析中的联盟形式背景[23]。进一步,对称概念对应等联盟概念,对称概念集SC对应等联盟概念集,对称概念的外延(或内涵)对应极大联盟。 因此,在冲突分析中对称形式背景及对称概念格可被用于获取代理人的极大联盟。 社交网络[24, 29-30]是由许多节点构成的一种社会结构,节点通常指用户,而用户之间有着各种社会关系。社交网络可表示为包含节点和边的图,其中节点表示用户,节点之间有边相连表示用户之间有关,如图4所示。 图4 社交网络Fig.4 Social network 在社交网络中,用户通常因为共同的兴趣和目的聚集在几个社区中,并进行大量的社交互动。因此,社区检测是社交网络中的一项重要研究内容。Tang等将社交网络与FCA相结合,提出了一种化学结构检索方法[29]。Hao等给出了利用FCA进行k-团(k-clique)检测的算法[24]。具体地,Hao等首先定义了修正邻接矩阵以建立形式背景[24]。图4所对应的形式背景同表2,其中,6个对象(或属性)表示6个节点,对于任意的xi,xj∈G,xiIxj表示节点xi与xj之间有边。因此,对称形式背景的二元关系I直接对应社交网络中的修正邻接矩阵。 此外,Hao等称修正邻接矩阵形成的形式背景中外延等于内涵的概念为等势概念(equiconcept),进一步,若等势概念的外延(或内涵)的模为k,则称为k-等势概念, (k-equiconcept)。 并证明了k-等势概念的外延(或内涵)为k-团, 如图5所示, 同一个椭圆虚线内的节点构成一个k-团, 图5中有3个3-团, 1个2-团。 由此, 对称概念对应等势概念, 对称概念集SC对应等势概念集, 外延(或内涵)的模为k的对称概念的外延(或内涵)对应k-团。 因此,在社交网络中对称形式背景及对称概念格可应用于k-团社区检测。 本文首先定义对称形式背景,讨论对称形式背景概念及概念格的特征,并给出对称概念的定义;其次,证明对称概念集SC是概念约简并探讨SC的性质;最后,从冲突分析及社交网络的角度解释对称形式背景、对称概念及SC的实际语义及应用。 关于对称形式背景还有很多新问题亟待提出和解决。如对称形式背景的二元关系满足自反性和对称性,若在此基础上附加传递性,那么同时满足自反性、对称性和传递性的形式背景对应着何种应用场景、有何更特殊的性质等都是值得探讨的问题。
2 对称形式背景及其性质


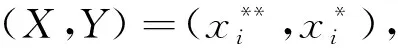

3 对称概念构造的概念约简
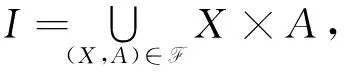
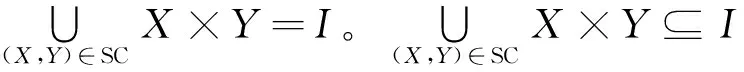



4 对称形式背景及对称概念格的应用
4.1 对称形式背景在冲突分析中的应用

4.2 对称形式背景在社交网络中的应用

5 结语

